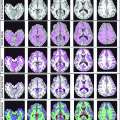
-norm, on the sparse data. The method is tested on MRI images and it is also compared to the weighted Compressed Sensing. Some results are reported and discussed.
Keywords
Magnetic resonance imaging (MRI)Compressed sensing (CS) 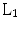 -normRadial adaptive acquisitionHomotopic
-normRadial adaptive acquisitionHomotopic 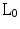 -norm.
-norm.1 Introduction
Magnetic Resonance Imaging (MRI) has become a major non invasive imaging modality over the past 25 years, due to its ability to provide structural details of human body, like Computed Tomography, and additional information on physiological status and pathologies, like nuclear medicine. The reconstruction of a single image usually involves collecting a series of trajectories. The measurement of a trajectory is a sampling process of a function evolving with time in a 2D or 3D space domain, referred to as “k-space”. The raw data from this sequence of acquisitions are then used to reconstruct an image by using the Fast Fourier Transform after gridding [8, 13].
The most popular k-space trajectories are straight lines from a Cartesian grid, in which each k-space line corresponds to the frequency encoding readout at each value of the phase encoding gradient (Spin Warp Imaging [6]). The lines in the grid are parallel and are equally separated. Although the acquisition of Cartesian trajectories allows easier image reconstruction, recent advances in MR hardware allow other acquisition patterns, such as spirals [12], or radial trajectories (Projection Reconstruction [9]). PR, for example, has many advantages over the conventional Cartesian k-space trajectory, because of its robustness to the motion artifacts, such those due to blood flow or respiration.
A fundamental limitation of MRI is the linear relation between the number of acquired trajectories and net scan time: minutes are often required to collect a complete data set. Such duration can be too high when dynamic processes have to be observed at high temporal resolution, such as in fMRI studies [2]. The acquisition time for each trajectory is limited by the slow natural relaxation processes, which are beyond the control of the acquisition sequence, and have to be respected. Therefore, the only way to speed up acquisition is to reduce the trajectories, that is by using undersampling.
Undersampling is the violation of the Nyquist’s criterion where images are reconstructed by using a number of data lower than that theoretically required to obtain a fully-sampled image. One of these methods [16] presented a k-space adaptive acquisition technique for MRI from projections. The method defined the entropy function on the power spectrum of the collected projections, to evaluate their information content, thus driving the acquisition where data variability is maximum. The choice of the projections was made during the acquisition process; this allowed the reduction of acquisition time, by reducing the scanned directions. A modified Fourier reconstruction algorithm, including an interpolation method [15], was used to reconstruct the image from the sparse set of projections. Other authors [3, 5, 7, 11, 20] presented the theory of Compressed Sensing (CS) and the details of its implementation for rapid MRI. They demonstrated that if the underlying image exhibits sparsity in some transform domain, then the image can be recovered from randomly undersampled frequency domain data, providing that an appropriate nonlinear recovery scheme is used. Most of the CS applications used the 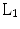 -norm minimization as reconstruction method. Recently, to improve image quality while reducing the number of collected data even below that required by
-norm minimization as reconstruction method. Recently, to improve image quality while reducing the number of collected data even below that required by 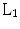 -norm reconstruction, an alternative non linear reconstruction formulation has been proposed [18, 19] based on homotopic approximation of the
-norm reconstruction, an alternative non linear reconstruction formulation has been proposed [18, 19] based on homotopic approximation of the 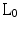 -norm. Besides, nonlinear reconstruction can be also improved by increasing samples in the central part of the k-space (low frequency terms contain more energy than high frequency terms, as demonstrated in weighed CS [10, 21]).
-norm. Besides, nonlinear reconstruction can be also improved by increasing samples in the central part of the k-space (low frequency terms contain more energy than high frequency terms, as demonstrated in weighed CS [10, 21]).
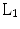 -norm minimization as reconstruction method. Recently, to improve image quality while reducing the number of collected data even below that required by
-norm minimization as reconstruction method. Recently, to improve image quality while reducing the number of collected data even below that required by 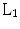 -norm reconstruction, an alternative non linear reconstruction formulation has been proposed [18, 19] based on homotopic approximation of the
-norm reconstruction, an alternative non linear reconstruction formulation has been proposed [18, 19] based on homotopic approximation of the 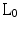 -norm. Besides, nonlinear reconstruction can be also improved by increasing samples in the central part of the k-space (low frequency terms contain more energy than high frequency terms, as demonstrated in weighed CS [10, 21]).
-norm. Besides, nonlinear reconstruction can be also improved by increasing samples in the central part of the k-space (low frequency terms contain more energy than high frequency terms, as demonstrated in weighed CS [10, 21]).In this Chapter an adaptive acquisition sequence and reconstruction is presented. It is based on some significant characteristics of CS (random sampling of spectral coefficients and 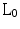 –minimization), combined with a radial adaptive acquisition criteria. Numerical simulations are reported and compared with weighted CS to show its performances.
–minimization), combined with a radial adaptive acquisition criteria. Numerical simulations are reported and compared with weighted CS to show its performances.
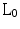 –minimization), combined with a radial adaptive acquisition criteria. Numerical simulations are reported and compared with weighted CS to show its performances.
–minimization), combined with a radial adaptive acquisition criteria. Numerical simulations are reported and compared with weighted CS to show its performances.2 Compressed Sensing and the Reconstruction Problem
Being the proposed method a joint usage of a radial adaptive acquisition criterion into a Compressed Sensing strategy, the following section presents an overview on CS theory and non linear reconstruction.
Let f be an image, the theoretical image, of interest defined on the domain 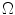 and suppose there exists a transformation,
and suppose there exists a transformation, 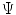 , such that the
, such that the 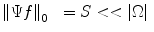 , i.e. the signal
, i.e. the signal  f is sparse in a transform
f is sparse in a transform  domain. The key idea of Compressed Sensing is to exploit this a priori knowledge to the fullest degree and to assert conditions under which a signal can be exactly reconstructed from a limited set of measurements of the order of S, certainly lower than
domain. The key idea of Compressed Sensing is to exploit this a priori knowledge to the fullest degree and to assert conditions under which a signal can be exactly reconstructed from a limited set of measurements of the order of S, certainly lower than 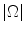 . When the unknowns are more than the acquired measurements, the problem to recover f becomes underdetermined, that is admitting infinite solutions. One choice for finding a solution u from this infinite set is to use the
. When the unknowns are more than the acquired measurements, the problem to recover f becomes underdetermined, that is admitting infinite solutions. One choice for finding a solution u from this infinite set is to use the 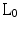 -norm by solving:
-norm by solving:
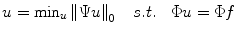 where the zero quasi-norm,
where the zero quasi-norm, 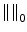 is a measure of functional cardinality (i.e. the number of nonzero coefficients on the sparse representation) and
is a measure of functional cardinality (i.e. the number of nonzero coefficients on the sparse representation) and 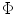 denotes the undersampled Fourier transform, corresponding to one of the chosen k-space undersampling schemes. The constraint
denotes the undersampled Fourier transform, corresponding to one of the chosen k-space undersampling schemes. The constraint 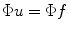 requires to consider images producing the same observed measurements. This problem yields a unique solution by finding the sparsest vector u in the solutions space. For images with S nonzero coefficients in
requires to consider images producing the same observed measurements. This problem yields a unique solution by finding the sparsest vector u in the solutions space. For images with S nonzero coefficients in 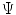 , the sparsest vector recovery with
, the sparsest vector recovery with 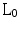 reconstruction is possible with only 2S observed measurements [4], substantially lower than that required by Nyquist’s criterion (
reconstruction is possible with only 2S observed measurements [4], substantially lower than that required by Nyquist’s criterion (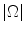 ). Despite the obvious potential for drastic reductions in net scan time, the
). Despite the obvious potential for drastic reductions in net scan time, the 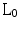 minimization problem requires a combinatorial search through all
minimization problem requires a combinatorial search through all 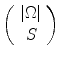 potential solutions to recover a S-sparse signal on
potential solutions to recover a S-sparse signal on 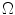 . It is a non-deterministic polynomial-time hard (NP hard) problem, intractable for any practical application. Another approach is to choose the
. It is a non-deterministic polynomial-time hard (NP hard) problem, intractable for any practical application. Another approach is to choose the 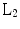 -norm to find the solution with minimum energy:
-norm to find the solution with minimum energy:
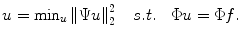 However, this solution may contain significant artifacts such as aliasing and blurring in practical situations, thus resulting in an image of low diagnostic value.
However, this solution may contain significant artifacts such as aliasing and blurring in practical situations, thus resulting in an image of low diagnostic value.
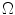 and suppose there exists a transformation,
and suppose there exists a transformation, 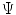 , such that the
, such that the 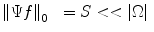 , i.e. the signal
, i.e. the signal 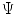 f is sparse in a transform
f is sparse in a transform 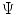 domain. The key idea of Compressed Sensing is to exploit this a priori knowledge to the fullest degree and to assert conditions under which a signal can be exactly reconstructed from a limited set of measurements of the order of S, certainly lower than
domain. The key idea of Compressed Sensing is to exploit this a priori knowledge to the fullest degree and to assert conditions under which a signal can be exactly reconstructed from a limited set of measurements of the order of S, certainly lower than 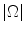 . When the unknowns are more than the acquired measurements, the problem to recover f becomes underdetermined, that is admitting infinite solutions. One choice for finding a solution u from this infinite set is to use the
. When the unknowns are more than the acquired measurements, the problem to recover f becomes underdetermined, that is admitting infinite solutions. One choice for finding a solution u from this infinite set is to use the 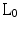 -norm by solving:
-norm by solving: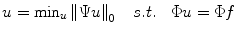
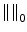 is a measure of functional cardinality (i.e. the number of nonzero coefficients on the sparse representation) and
is a measure of functional cardinality (i.e. the number of nonzero coefficients on the sparse representation) and 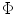 denotes the undersampled Fourier transform, corresponding to one of the chosen k-space undersampling schemes. The constraint
denotes the undersampled Fourier transform, corresponding to one of the chosen k-space undersampling schemes. The constraint 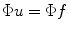 requires to consider images producing the same observed measurements. This problem yields a unique solution by finding the sparsest vector u in the solutions space. For images with S nonzero coefficients in
requires to consider images producing the same observed measurements. This problem yields a unique solution by finding the sparsest vector u in the solutions space. For images with S nonzero coefficients in 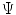 , the sparsest vector recovery with
, the sparsest vector recovery with 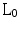 reconstruction is possible with only 2S observed measurements [4], substantially lower than that required by Nyquist’s criterion (
reconstruction is possible with only 2S observed measurements [4], substantially lower than that required by Nyquist’s criterion (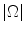 ). Despite the obvious potential for drastic reductions in net scan time, the
). Despite the obvious potential for drastic reductions in net scan time, the 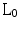 minimization problem requires a combinatorial search through all
minimization problem requires a combinatorial search through all 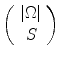 potential solutions to recover a S-sparse signal on
potential solutions to recover a S-sparse signal on 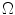 . It is a non-deterministic polynomial-time hard (NP hard) problem, intractable for any practical application. Another approach is to choose the
. It is a non-deterministic polynomial-time hard (NP hard) problem, intractable for any practical application. Another approach is to choose the 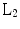 -norm to find the solution with minimum energy:
-norm to find the solution with minimum energy: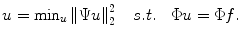
Following that, several authors [3, 5, 11] demonstrated that if one relaxes the 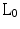 -norm to the
-norm to the 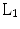 -norm, a sparse image f can be exactly recovered by using the following convex optimization problem:
-norm, a sparse image f can be exactly recovered by using the following convex optimization problem:
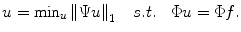 In most medical imaging applications including MRI, signals are rarely noise-free and it is desirable to investigate how measurement error affects the stability of the reconstruction program. To include the presence of experimental noise into the reconstruction process, the convex optimization is reformulated as follows:
In most medical imaging applications including MRI, signals are rarely noise-free and it is desirable to investigate how measurement error affects the stability of the reconstruction program. To include the presence of experimental noise into the reconstruction process, the convex optimization is reformulated as follows:
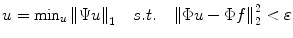 where
where 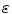 controls the fidelity of the reconstruction to the k-space measured data
controls the fidelity of the reconstruction to the k-space measured data 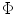 f, whose choice is dependent on the noise level in the collected data (it is usually set below the expected noise level). Though this approach cannot generally be achieved at the true minimum sampling rate associable with the
f, whose choice is dependent on the noise level in the collected data (it is usually set below the expected noise level). Though this approach cannot generally be achieved at the true minimum sampling rate associable with the 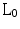 case, it offers the ability to sample below the Nyquist rate and performs the recovery with a computationally tractable procedure. Numerical experiments [3] suggested that, for a good reconstruction with
case, it offers the ability to sample below the Nyquist rate and performs the recovery with a computationally tractable procedure. Numerical experiments [3] suggested that, for a good reconstruction with 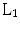 -norm, the number of measured k-space samples,
-norm, the number of measured k-space samples, 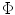 f, should be roughly 3S
f, should be roughly 3S 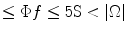 (an increase of
(an increase of 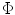 f towards 5S would improve the reconstruction).
f towards 5S would improve the reconstruction).
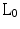 -norm to the
-norm to the 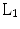 -norm, a sparse image f can be exactly recovered by using the following convex optimization problem:
-norm, a sparse image f can be exactly recovered by using the following convex optimization problem: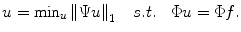
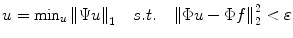
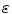 controls the fidelity of the reconstruction to the k-space measured data
controls the fidelity of the reconstruction to the k-space measured data 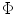 f, whose choice is dependent on the noise level in the collected data (it is usually set below the expected noise level). Though this approach cannot generally be achieved at the true minimum sampling rate associable with the
f, whose choice is dependent on the noise level in the collected data (it is usually set below the expected noise level). Though this approach cannot generally be achieved at the true minimum sampling rate associable with the 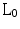 case, it offers the ability to sample below the Nyquist rate and performs the recovery with a computationally tractable procedure. Numerical experiments [3] suggested that, for a good reconstruction with
case, it offers the ability to sample below the Nyquist rate and performs the recovery with a computationally tractable procedure. Numerical experiments [3] suggested that, for a good reconstruction with 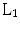 -norm, the number of measured k-space samples,
-norm, the number of measured k-space samples, 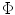 f, should be roughly 3S
f, should be roughly 3S 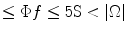 (an increase of
(an increase of 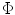 f towards 5S would improve the reconstruction).
f towards 5S would improve the reconstruction).On the other hand, the reconstruction problem proposed by Trzasko et al. [18, 19] attacked directly the ideal 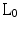




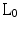
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree