(1)
Intelligent Systems Research Centre, University of Ulster, Londonderry, UK
Abstract
This chapter deals with the random effects in fMRI data analysis. To begin with, we give the background in using the mixed-effect model for second-level fMRI data processing. Because applying general linear mixed model (GLMM) method directly to second-level fMRI data analysis can lead to computational difficulties, we employ a method which projects the first-level variance for the second-level analysis, i.e., we adopt a two-stage mixed model to combine or compare different subjects. To estimate the variance for the mixed model analysis, we developed an expectation trust region algorithm. We provide detailed information about Newton–Raphson (NR) and (expectation) trust region algorithms for different run/subject combination and comparison. After the parameters have been estimated, the T statistic for significance inference was employed. Simulation studies using synthetic data were carried out to evaluate the accuracy of the methods for group combination and comparison. In addition, real fMRI dataset from retinotopic mapping experiment was employed to test the feasibility of the methods for second-level analysis. To improve the NR algorithm, we present Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm for the mixed model parameters estimation. We found that the method can improve the estimation for NR algorithm, but no significant improvement for trust region algorithms. Finally, we proposed an approach for degree of freedom (DF) estimation in the mixed-effect model. The idea is based on robust statistics. Using maximum-likelihood estimation method, we calculate the score function and Hessian matrices for the iteration expectation trust region algorithm for maximizing likelihood function. We then give NR and (expectation) trust region iteration algorithms for the DF estimation.
Keywords
Variance analysisNumerical analysisTrust region algorithmMixed-effect modelRandom effectfMRI second-level analysis3.1 Mixed Model for fMRI Data Analysis
Generally speaking, models that contain both fixed and random effects are called mixed (effect) models. Fixed effects are the effects attributable to a finite set of levels of a factor that occur in the data and which are there because we are interested in them. Models in which the only effects are fixed effects are called fixed effects models, or sometimes just fixed models. Those having (apart from a single, general mean common to all observations) only random effects are called random effects models or, more simply, random models [1]. If there are attributable to usually infinite set of levels of a factor, of which only a random sample is deemed to occur in the data, we call this as random effects.
Mixed model [2] is commonly applied for correlated data. The popularity of applying this method is largely due to the rapid expansion in the availability of software and theory development. There is a number of books to introduce this model in statistical analysis [3] and numerous papers about the model parameters estimation, inference, and statistical test [4–8]. This model is especially useful for repeated measure, longitudinal dataset analysis [9], growth model, multilevel model, and hierarchical models. Initially, this method was developed to estimate random and fixed effects for animal breading studies [2]. Later, several methods have been proposed to estimate variance parameters in the framework of linear mixed models, including two commonly used methods, i.e., maximum-likelihood (ML) estimation [10] and residual/restrict maximum-likelihood (REML) estimation [11]. Because the log-likelihood function is often a nonlinear function of model parameters and variance parameters, numerical methods need to be used to optimize the objective function. Although a wide variety of iterative techniques are available to achieve this goal, these methods are fundamentally built on two basic approaches: the expectation maximization [12, 13] and the Newton–Raphson (NR) algorithm [7]. Since most of papers and books use EM algorithm for variance parameters estimation in the mixed model, we will introduce the Levenberg–Marquardt (LM) algorithm and (expectation) trust region algorithm for the parameter estimation in second-level fMRI data analysis.
3.1.1 Fixed and Random Effects in fMRI Analysis
In fMRI data analysis, the hemodynamic response function (HRF) and drift effects at the first level can be regarded as fixed effect. To give an example, assume six subjects participated in an fMRI experiment, in which three different stimuli were employed. The effects due to the stimuli would be considered fixed effects (presumably we are interested in particular stimulus used), whereas the effects due to the subjects would be considered random effects because the subjects chosen would be considered a random sample of brain activation from some hypothetical, infinite population. Since there is definite interest in the particular stimulus used, the statistical concern is to estimate those stimuli that introduced HRF effects; they are fixed effect. No assumption is made that the stimuli are selected at random from a distribution of stimulus values. Since, in contrast, this kind of assumption has then been made about the subject effects, interest in them lies in estimating the variance of those effects. This chapter aims to develop numerical methods for variance estimation.
3.1.2 Generalized Linear Mixed Model for fMRI Study
Mixed model has the advantage of accounting for the fixed effect and (individual) random effect within one model; therefore, the fMRI response effects and the covariance of the response from different runs/subjects can be estimated within one model simultaneously. From statistical theory, we know that the general linear mixed model (GLMM) [4] can be used for this purpose which is expressed as
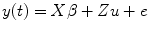
where X represents the design matrix for the fixed effect (experimental design and drift as shown in Chap. 2) from the first level; Z denotes the design matrix for the second level to model the random effect (individual effect); and y(t) is the fMRI response, u and β are predictors from first and second level analysis, where u ∼ (0,G), e ∼ (0,R), and y ∼ (Xβ, ZGZ T + R) and G and R are variance matrices. The maximum-likelihood solution of this model is as follows [2, 3]:
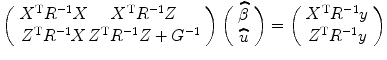
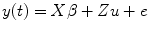
(3.1)
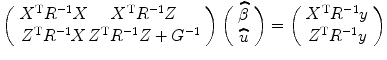
(3.2)
It is not too difficult to see that it is computationally demanding to solve Eq. (3.2) because of the following two reasons: First, the first-level parameters (β and R) need to be updated prior to estimating the second-level parameters which are obtained from both the first- and second-level parameters. Second, when a new subject is scanned, all the first-level parameters/results need to be estimated again, and it is very computationally demanding for the whole brain, i.e., voxel by voxel. For these reasons, two-stage or multilevel models were adopted by most fMRI studies [14–16]. The idea of two-stage model is to compute the mixed model in two steps, i.e., the first step is to calculate the linear model parameters, effects, and variance for the first-level analysis as we have shown in the previous chapter. In the second step, for different runs/subjects combination or comparison, variance and parameters are estimated by taking into account the variance and effect from the first-level analysis. The most prominent advantage of two-stage method is that in the second-level analysis, the information from the first level does not need to be updated; therefore, it reduces the computational burden. Due to its simplicity in computation for the second fMRI data analysis, we present two-stage model in the next section.
3.1.3 Mixed Model and Its Numerical Estimations
To simplify fMRI dataset analysis, we employ a two-stage method which separates the first-level or only considers the first-level variance and its projection onto the second level for second/higher-level fMRI data analysis [15–19]. In the implementation of a two-stage method for second-level analysis, expectation–maximization (EM) [12, 13] and Newton–Raphson (NR) algorithms are often employed [17, 19–21] to estimate the variance parameters in the residual/restricted maximum-likelihood/log-likelihood function (REML) [11]. REML corrects the bias in maximum-likelihood (ML) estimation [10] by accounting for the loss of degrees of freedom (df) attributable to estimation of the fixed effects. EM methods often have fairly simple forms and hence are easy to program; they do not take into account the second-order gradient (Hessian matrix). Rather, the method approximates the Hessian matrix using an expectation method. EM offers computational advantages over the NR method, as it does not have to compute second-order derivatives of the likelihood function or directly evaluate the full likelihood function.
The EM algorithm is an iterative method to estimate mixed model parameters starting from some initial guess. It has E step and M step in each iteration, and the algorithm finds the distribution of the unobserved variables in the E step while reestimates the parameters to be those with ML in the M step. This method has the advantage of robust to the starting values and numerical stable. The variance parameters from EM estimation are guaranteed to remain in the parameter space and the log-likelihood function does not decrease after each EM iteration. However, this method can be slow to converge, and many extensions such as expectation conditional maximization [5] and parameter-expanded EM algorithms [22] have developed to improve the convergence rate.
In contrast to EM algorithm, NR algorithm is widely used to solve the optimization problem, and it is faster in terms of convergence rate to optimize the log-likelihood objective function, but it needs second-order derivative of the objective function to get the Hessian matrix. One idea to overcome this limitation is to replace the Hessian matrix with its expectation, i.e., using Fisher information matrix to estimate Hessian matrix [11]. The advantage of this is that the expected information matrix is often easier to compute than the observed information matrix, although it may possibly increase the computational time. Moreover, the NR method is sensitive to initial parameter values. Although trust region optimization approaches such as Levenberg–Marquardt (LM) [23] have been proposed to circumvent this limitation, which may be initialized far off the final minimum/maximum [3, 7, 24], trust region algorithm for log-likelihood function optimization is not commonly applied for the mixed-effect model estimation [1]. The idea of trust region algorithm is to change LM damper factor or trust region in each numerical iteration. The LM parameter can be regarded as trust region where the model is a good approximation of objective function. It has been widely used for nonlinear optimization in numerical analysis [25, 26]. Trust region methods overcome the problems that linear search methods encounter with nonsymmetric positive definite approximate Hessians. Particularly, a Newton trust region strategy allows the use of complete Hessian information even in regions where the Hessian has negative curvature. In this specific trust region method, we can switch the steepest descent direction to the Newton direction in a way that have the global convergence properties of steepest descent and fast local convergence of Newton’s method [25]. In the next section, we will give detailed information about the implementation of trust region algorithms for mixed model in second-level fMRI data analysis.
3.2 Numerical Analysis for Mixed-Effect Models
From Chap. 2, for each run/subject, we obtained one effect map (e.g., Eq. (2.39) in Chap. 2) and one variance estimation map (e.g., Eq. (2.40) in Chap. 2) from the first level analysis. We take into account these variance and effect maps for the second-level data analysis. Specifically, we need to estimate the random effect from different runs/subjects for second-level fMRI data analysis.
3.2.1 Two-Stage Model for the Second-Level fMRI Analysis
For each voxel, the second-level model for fMRI data analysis can be described as [16]
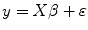
where y is the estimated effect from different runs/subjects at first level with
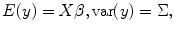
where X is n × p design matrix, and
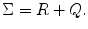
where R and Q denote fixed effect variance and random effect variance, respectively. If we average/combine different subjects, i.e., we set ![$$ X={\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill \dots \hfill & \hfill 1\hfill \end{array}\right]}^{\mathrm{T}} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_IEq1.gif) , then R = diag(S 12,S 22, …,S n 2), where S 1, S 2, … S n are the standard deviation from run/subject 1, 2,…n, calculated from Eq. (2.40) in Chap. 2. R shows the projection of first-level variance onto the second-level analysis. The covariance components Q = σ 2 random I [17], where I is the n × n identity matrix and n is the total number of runs/subjects to be combined within the mixed-effect model, and
, then R = diag(S 12,S 22, …,S n 2), where S 1, S 2, … S n are the standard deviation from run/subject 1, 2,…n, calculated from Eq. (2.40) in Chap. 2. R shows the projection of first-level variance onto the second-level analysis. The covariance components Q = σ 2 random I [17], where I is the n × n identity matrix and n is the total number of runs/subjects to be combined within the mixed-effect model, and
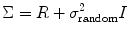
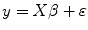
(3.3)
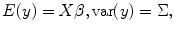
(3.4)
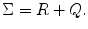
(3.5)
![$$ X={\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill \dots \hfill & \hfill 1\hfill \end{array}\right]}^{\mathrm{T}} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_IEq1.gif) , then R = diag(S 12,S 22, …,S n 2), where S 1, S 2, … S n are the standard deviation from run/subject 1, 2,…n, calculated from Eq. (2.40) in Chap. 2. R shows the projection of first-level variance onto the second-level analysis. The covariance components Q = σ 2 random I [17], where I is the n × n identity matrix and n is the total number of runs/subjects to be combined within the mixed-effect model, and
, then R = diag(S 12,S 22, …,S n 2), where S 1, S 2, … S n are the standard deviation from run/subject 1, 2,…n, calculated from Eq. (2.40) in Chap. 2. R shows the projection of first-level variance onto the second-level analysis. The covariance components Q = σ 2 random I [17], where I is the n × n identity matrix and n is the total number of runs/subjects to be combined within the mixed-effect model, and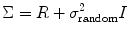
(3.6)
σ 2 random is the random effects variance from the second-level fMRI data analysis. If we want to compare two different groups, i.e., controls with patients, we can set the design matrix in Eq. (3.3) as ![$$ X={\left[\begin{array}{ccccc}\hfill 1\hfill & \hfill 1\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right]}^{\mathrm{T}} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_IEq2.gif) , where 1 in the bottom row corresponds to the total number of controls (n 1) and 1 in the top row corresponds to the total number of patients (n 2). In this case and consider Kronecker product covariance structure, we have the variance in the following form:
, where 1 in the bottom row corresponds to the total number of controls (n 1) and 1 in the top row corresponds to the total number of patients (n 2). In this case and consider Kronecker product covariance structure, we have the variance in the following form:
![$$ \Sigma =R+Q=\left[\begin{array}{ll} {R}_1& 0\\ 0& \hfill {R}_2\hfill \end{array}\right]+\left[\begin{array}{ll} {\sigma}_1^2\hfill & {\sigma}_{12}\hfill \\ {\sigma}_{12}\hfill & \hfill {\sigma}_2^2\hfill \end{array}\right]\otimes A $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ7.gif)
where R 1 and R 2 are the control and patient group variance from the first-level analysis, respectively (obtained from Eq. (2.40) in Chap. 2); ⊗ is Kronecker product; A is relationship matrix (in our study, we set A = I with appropriate dimensions); σ 12, σ 22, and σ 12 are the random effects variance/covariance of the two groups from the second-level fMRI data analysis; and β in Eq. (3.3) and random effects variance/covariance, e.g., σ 2 random, in Eq. (3.6) or σ 12, σ 22, and σ 12 in Eq. (3.7), are the parameters that need to be identified.
![$$ X={\left[\begin{array}{ccccc}\hfill 1\hfill & \hfill 1\hfill & \hfill \dots \hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right]}^{\mathrm{T}} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_IEq2.gif) , where 1 in the bottom row corresponds to the total number of controls (n 1) and 1 in the top row corresponds to the total number of patients (n 2). In this case and consider Kronecker product covariance structure, we have the variance in the following form:
, where 1 in the bottom row corresponds to the total number of controls (n 1) and 1 in the top row corresponds to the total number of patients (n 2). In this case and consider Kronecker product covariance structure, we have the variance in the following form:![$$ \Sigma =R+Q=\left[\begin{array}{ll} {R}_1& 0\\ 0& \hfill {R}_2\hfill \end{array}\right]+\left[\begin{array}{ll} {\sigma}_1^2\hfill & {\sigma}_{12}\hfill \\ {\sigma}_{12}\hfill & \hfill {\sigma}_2^2\hfill \end{array}\right]\otimes A $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ7.gif)
(3.7)
3.2.2 Maximum-Likelihood Method for Variance Estimation
From multivariate statistical analysis [27] and maximum-likelihood estimation (Appendix A), we know that the probability density of the data y in Eq. (3.3) has the form of the multivariate normal distribution [3], i.e.,
![$$ f\left(y;\beta, \Sigma \right)={\left(2\pi \right)}^{-\frac{n}{2}}{\left|\Sigma \right|}^{-\frac{1}{2}} \exp \left[-\frac{1}{2}{\left(y- X\beta \right)}^{\mathrm{T}}\Sigma {}^{-1}\left(y- X\beta \right)\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ8.gif)
![$$ f\left(y;\beta, \Sigma \right)={\left(2\pi \right)}^{-\frac{n}{2}}{\left|\Sigma \right|}^{-\frac{1}{2}} \exp \left[-\frac{1}{2}{\left(y- X\beta \right)}^{\mathrm{T}}\Sigma {}^{-1}\left(y- X\beta \right)\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ8.gif)
(3.8)
Taking the natural logarithm of the expression on the right side of Eq. (3.8) yields the log-likelihood of β and Σ given the observed data (y,X) as [1, 13, 27]
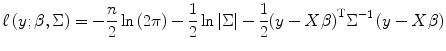
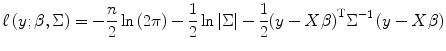
(3.9)
From numerical analysis [26] or Appendix B, Newton–Raphson (NR) method estimates the parameters θ = (β,Σ) as
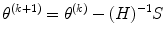
where 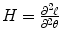 is Hessian matrix and
is Hessian matrix and 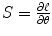 is the score function.
is the score function.
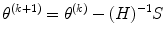
(3.10)
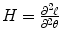 is Hessian matrix and
is Hessian matrix and 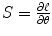 is the score function.
is the score function.3.2.3 Different Runs Combination
To give an example for applying this method to combine different runs within subject, we calculate score function and Hessian matrix for maximization of the log-likelihood function. From matrix theory [1], we use
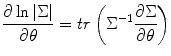
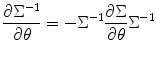
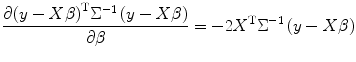
where tr is trace of matrix. To estimate random effect, from Eq. (3.9) we obtain the score function for random effect variance estimation as
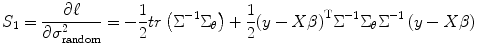
where 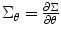 . If we average different runs/subjects, we substitute Eq. (3.6) into (3.14) to estimate the random effect in the second-level analysis, i.e., θ = σ 2 random, and we have
. If we average different runs/subjects, we substitute Eq. (3.6) into (3.14) to estimate the random effect in the second-level analysis, i.e., θ = σ 2 random, and we have
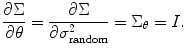
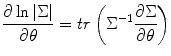
(3.11)
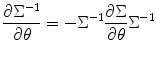
(3.12)
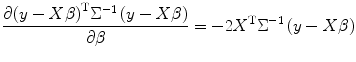
(3.13)
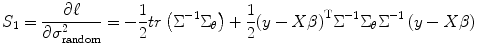
(3.14)
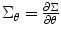 . If we average different runs/subjects, we substitute Eq. (3.6) into (3.14) to estimate the random effect in the second-level analysis, i.e., θ = σ 2 random, and we have
. If we average different runs/subjects, we substitute Eq. (3.6) into (3.14) to estimate the random effect in the second-level analysis, i.e., θ = σ 2 random, and we have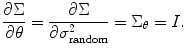
(3.15)
Then the score function for estimate variance can be expressed (from Eqs. (3.14) and (3.15)) as
![$$ {S}_1=\frac{\partial {\ell}}{\partial {\sigma}_{\mathrm{random}}^2}=\frac{1}{2}\left[- tr\left({\Sigma}^{-1}\right)+{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}{\Sigma}^{-1}\left(y- X\beta \right)\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ16.gif)
![$$ {S}_1=\frac{\partial {\ell}}{\partial {\sigma}_{\mathrm{random}}^2}=\frac{1}{2}\left[- tr\left({\Sigma}^{-1}\right)+{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}{\Sigma}^{-1}\left(y- X\beta \right)\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ16.gif)
(3.16)
Set S 2 = 0 to obtain β as
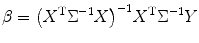
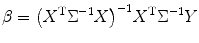
(3.18)
Then the total score function for estimating both variance and predictor can be written as matrix form S = [S 1,S 2]T. Next, we need to calculate Hessian matrix for the Newton-type iteration algorithm. From Eq. (3.16), we have
![$$ \begin{gathered}{H}_{11}=\dfrac{\partial^2{\ell}}{\partial^2\theta} = \dfrac{\partial {S}_1}{\partial {\sigma}_{\mathrm{random}}^2} = \dfrac{1}{2}\left[ tr\left({\Sigma}^{-1}{\Sigma}_{\theta }{\Sigma}^{-1}\right)\right.\\{}\left.-{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}{\Sigma}_{\theta }{\Sigma}^{-1}{\Sigma}^{-1}\left(y- X\beta \right)\right.\\ {}\kern1em \left.-{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}{\Sigma}^{-1}{\Sigma}_{\theta }{\Sigma}^{-1}\left(y- X\beta \right)\right]\end{gathered} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ19.gif)
![$$ \begin{gathered}{H}_{11}=\dfrac{\partial^2{\ell}}{\partial^2\theta} = \dfrac{\partial {S}_1}{\partial {\sigma}_{\mathrm{random}}^2} = \dfrac{1}{2}\left[ tr\left({\Sigma}^{-1}{\Sigma}_{\theta }{\Sigma}^{-1}\right)\right.\\{}\left.-{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}{\Sigma}_{\theta }{\Sigma}^{-1}{\Sigma}^{-1}\left(y- X\beta \right)\right.\\ {}\kern1em \left.-{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}{\Sigma}^{-1}{\Sigma}_{\theta }{\Sigma}^{-1}\left(y- X\beta \right)\right]\end{gathered} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ19.gif)
(3.19)
The Hessian matrix is
![$$ H=\left[\begin{array}{cc}\hfill {H}_{11}\hfill & \hfill {H}_{12}\hfill \\ {}\hfill {H}_{12}\hfill & \hfill {H}_{22}\hfill \end{array}\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ23.gif)
![$$ H=\left[\begin{array}{cc}\hfill {H}_{11}\hfill & \hfill {H}_{12}\hfill \\ {}\hfill {H}_{12}\hfill & \hfill {H}_{22}\hfill \end{array}\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ23.gif)
(3.23)
We may take the expectation of the Hessian matrix H by substituting E(y − Xβ) = 0 into Eqs. (3.19, 3.20, 3.21, 3.22, and 3.23), which leads to the information matrix (IM) as
![$$ F=E(H)=\left[\begin{array}{c@{}c} \dfrac{1}{2} tr\left({\left({\Sigma}^{-1}\right)}^2\right) & 0 \\ 0 & -{X}^{\mathrm{T}}{\Sigma}^{-1}X \end{array}\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ24.gif)
![$$ F=E(H)=\left[\begin{array}{c@{}c} \dfrac{1}{2} tr\left({\left({\Sigma}^{-1}\right)}^2\right) & 0 \\ 0 & -{X}^{\mathrm{T}}{\Sigma}^{-1}X \end{array}\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ24.gif)
(3.24)
If we use IM to replace Hessian matrix in Eq. (3.10) for the NR algorithm, which leads to new iterative NR method,
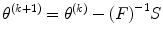
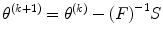
(3.25)
To achieve likelihood maximization, representing θ = [σ 2 random,β]T and considering Eq. (3.10), the iteration algorithm for variance and predictor estimation can be expressed as
![$$ {\left[\begin{array}{c}\hfill {\widehat{\sigma}}_{\mathrm{random}}^2\hfill \\ {}\hfill \widehat{\beta}\hfill \end{array}\right]}^{\left(k+1\right)}={\left[\begin{array}{c}\hfill {\widehat{\sigma}}_{\mathrm{random}}^2\hfill \\ {}\hfill \widehat{\beta}\hfill \end{array}\right]}^{(k)}-{H}^{-1}\left({\widehat{\theta}}^{(k)}\right){\left[\begin{array}{c}\hfill {S}_1\left(\widehat{\theta}\right)\hfill \\ {}\hfill {S}_2\left(\widehat{\theta}\right)\hfill \end{array}\right]}^{(k)} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ26.gif)
where H is the Hessian matrix which can be replaced by IM F in Eq. (3.24) and k is number of iteration.
![$$ {\left[\begin{array}{c}\hfill {\widehat{\sigma}}_{\mathrm{random}}^2\hfill \\ {}\hfill \widehat{\beta}\hfill \end{array}\right]}^{\left(k+1\right)}={\left[\begin{array}{c}\hfill {\widehat{\sigma}}_{\mathrm{random}}^2\hfill \\ {}\hfill \widehat{\beta}\hfill \end{array}\right]}^{(k)}-{H}^{-1}\left({\widehat{\theta}}^{(k)}\right){\left[\begin{array}{c}\hfill {S}_1\left(\widehat{\theta}\right)\hfill \\ {}\hfill {S}_2\left(\widehat{\theta}\right)\hfill \end{array}\right]}^{(k)} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ26.gif)
(3.26)
However, to estimate these parameters together can lead to numerical instability; this is also true for our study. Therefore, as many previous studies, we adopt the method to calculate predictor and variance separately. This is easy to achieve, since we can update random effect variance using S = S 1 and H = H 11. In the meantime, we also need to update predictors using Eq. (3.18) in each iteration. Similar to Eq. (3.24), we can replace the Hessian matrix H 11 and H 22 by using 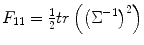 and F 22 = − X TΣ− 1 X for variance and predictor estimation, respectively.
and F 22 = − X TΣ− 1 X for variance and predictor estimation, respectively.
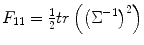 and F 22 = − X TΣ− 1 X for variance and predictor estimation, respectively.
and F 22 = − X TΣ− 1 X for variance and predictor estimation, respectively.3.2.4 Group Comparison in the Mixed Model
To compare different groups, we use the variance matrix as shown in Eq. (3.7) and set θ = σ 12, A = I, and we get [1]
![$$ {\Sigma}_{\theta }=\frac{\partial \Sigma}{\partial \theta }=\frac{\partial \Sigma}{\partial {\sigma}_1^2}=\left[\begin{array}{c@{}c} 1 & 0 \\ {} 0 & 0 \end{array}\right]\otimes I=\left[\begin{array}{c@{}c} {I}_{n1} & 0 \\ {} 0 & 0 \end{array}\right]={\Sigma}_1, $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ27.gif)
where I n1 is the n 1 × n 1 identity matrix and n 1 is the number of control subject. From Eqs. (3.14) and (3.27), the score function of σ 12 becomes
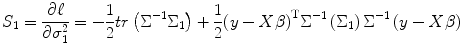
![$$ {\Sigma}_{\theta }=\frac{\partial \Sigma}{\partial \theta }=\frac{\partial \Sigma}{\partial {\sigma}_1^2}=\left[\begin{array}{c@{}c} 1 & 0 \\ {} 0 & 0 \end{array}\right]\otimes I=\left[\begin{array}{c@{}c} {I}_{n1} & 0 \\ {} 0 & 0 \end{array}\right]={\Sigma}_1, $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ27.gif)
(3.27)
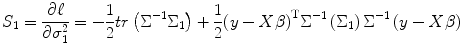
(3.28)
Similarly, we obtain score function S 2 using
![$$ {\Sigma}_{\theta }=\frac{\partial \Sigma}{\partial \theta }=\frac{\partial \Sigma}{\partial {\sigma}_{12}}=\left[\begin{array}{c@{}c}\hfill 0\hfill & \hfill 1\hfill \\ {}\hfill 1\hfill & \hfill 0\hfill \end{array}\right]\otimes I=\left[\begin{array}{c@{}c}\hfill 0\hfill & \hfill {I}_{n1\times n2}\hfill \\ {}\hfill {I}_{n2\times n1}\hfill & \hfill 0\hfill \end{array}\right]={\Sigma}_2 $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ29.gif)
where I n1 × n2 and I n2 × n1 are the n 1 × n 2 and n 2 × n 1 identity matrices, respectively. In addition, from Eqs. (3.7) and (3.29), we get
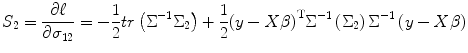
![$$ {\Sigma}_{\theta }=\frac{\partial \Sigma}{\partial \theta }=\frac{\partial \Sigma}{\partial {\sigma}_{12}}=\left[\begin{array}{c@{}c}\hfill 0\hfill & \hfill 1\hfill \\ {}\hfill 1\hfill & \hfill 0\hfill \end{array}\right]\otimes I=\left[\begin{array}{c@{}c}\hfill 0\hfill & \hfill {I}_{n1\times n2}\hfill \\ {}\hfill {I}_{n2\times n1}\hfill & \hfill 0\hfill \end{array}\right]={\Sigma}_2 $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ29.gif)
(3.29)
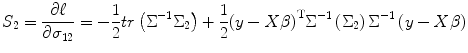
(3.30)
Using
![$$ {\Sigma}_{\theta }=\frac{\partial \Sigma}{\partial \theta }=\frac{\partial \Sigma}{\partial {\sigma}_2^2}=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 1\hfill \end{array}\right]\otimes I=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill {I}_{n2}\hfill \end{array}\right]={\Sigma}_3, $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ31.gif)
and taking into account Eq. (3.14), we obtain the score function of σ 22 as
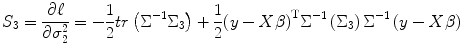
where I n2 is n 2 × n 2 identity matrix and n 2 is number of patient subject. The score function has the form of S = [S 1,S 2,S 3]T, and the corresponding Hessian matrix is
![$$ H=\left[\begin{array}{ccc}\hfill {H}_{11}\hfill & \hfill {H}_{12}\hfill & \hfill {H}_{13}\hfill \\ {}\hfill {H}_{12}\hfill & \hfill {H}_{22}\hfill & \hfill {H}_{23}\hfill \\ {}\hfill {H}_{13}\hfill & \hfill {H}_{23}\hfill & \hfill {H}_{33}\hfill \end{array}\right]=\left[\arraycolsep3pt\begin{array}{ccc}\hfill \dfrac{\partial {S}_1}{\partial {\sigma}_1^2}\hfill & \hfill \dfrac{\partial {S}_1}{\partial {\sigma}_{12}}\hfill & \hfill \dfrac{\partial {S}_1}{\partial {\sigma}_2^2}\hfill \\[8pt] {}\hfill \dfrac{\partial {S}_1}{\partial {\sigma}_{12}}\hfill & \hfill \dfrac{\partial {S}_2}{\partial {\sigma}_{12}}\hfill & \hfill \dfrac{\partial {S}_2}{\partial {\sigma}_2^2}\hfill \\[8pt] {}\hfill \dfrac{\partial {S}_1}{\partial {\sigma}_2^2}\hfill & \hfill \dfrac{\partial {S}_2}{\partial {\sigma}_2^2}\hfill & \hfill \dfrac{\partial {S}_3}{\partial {\sigma}_2^2}\hfill \end{array}\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ33.gif)
where H 11, H 12, H 13, H 22, H 23, and H 33 are calculated as follows. From Eqs. (3.19), (3.27), and (3.28), we get
![$$ \begin{aligned}[b] {H}_{11}=\frac{\partial {S}_1}{\partial {\sigma}_1^2}=&\frac{1}{2}\left[ {\it tr}\left({\Sigma}^{-1}\left({\Sigma}_1\right){\Sigma}^{-1}\left({\Sigma}_1\right)\right)\right.\\[-3pt] & \quad \left.-2{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}\left({\Sigma}_1\right){\Sigma}^{-1}\left({\Sigma}_1\right){\Sigma}^{-1}\left(y- X\beta \right)\right] \end{aligned} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ34.gif)
![$$ {\Sigma}_{\theta }=\frac{\partial \Sigma}{\partial \theta }=\frac{\partial \Sigma}{\partial {\sigma}_2^2}=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 1\hfill \end{array}\right]\otimes I=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill {I}_{n2}\hfill \end{array}\right]={\Sigma}_3, $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ31.gif)
(3.31)
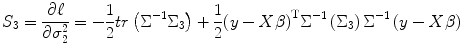
(3.32)
![$$ H=\left[\begin{array}{ccc}\hfill {H}_{11}\hfill & \hfill {H}_{12}\hfill & \hfill {H}_{13}\hfill \\ {}\hfill {H}_{12}\hfill & \hfill {H}_{22}\hfill & \hfill {H}_{23}\hfill \\ {}\hfill {H}_{13}\hfill & \hfill {H}_{23}\hfill & \hfill {H}_{33}\hfill \end{array}\right]=\left[\arraycolsep3pt\begin{array}{ccc}\hfill \dfrac{\partial {S}_1}{\partial {\sigma}_1^2}\hfill & \hfill \dfrac{\partial {S}_1}{\partial {\sigma}_{12}}\hfill & \hfill \dfrac{\partial {S}_1}{\partial {\sigma}_2^2}\hfill \\[8pt] {}\hfill \dfrac{\partial {S}_1}{\partial {\sigma}_{12}}\hfill & \hfill \dfrac{\partial {S}_2}{\partial {\sigma}_{12}}\hfill & \hfill \dfrac{\partial {S}_2}{\partial {\sigma}_2^2}\hfill \\[8pt] {}\hfill \dfrac{\partial {S}_1}{\partial {\sigma}_2^2}\hfill & \hfill \dfrac{\partial {S}_2}{\partial {\sigma}_2^2}\hfill & \hfill \dfrac{\partial {S}_3}{\partial {\sigma}_2^2}\hfill \end{array}\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ33.gif)
(3.33)
![$$ \begin{aligned}[b] {H}_{11}=\frac{\partial {S}_1}{\partial {\sigma}_1^2}=&\frac{1}{2}\left[ {\it tr}\left({\Sigma}^{-1}\left({\Sigma}_1\right){\Sigma}^{-1}\left({\Sigma}_1\right)\right)\right.\\[-3pt] & \quad \left.-2{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}\left({\Sigma}_1\right){\Sigma}^{-1}\left({\Sigma}_1\right){\Sigma}^{-1}\left(y- X\beta \right)\right] \end{aligned} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ34.gif)
(3.34)
Taking into account E(y − Xβ) = 0, it is easy to obtain Fisher IM as
![$$ F=E(H)=\frac{1}{2}\left[\begin{array}{ccc}\hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_1{\Sigma}^{-1}{\Sigma}_1\right)\hfill & \hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_2{\Sigma}^{-1}{\Sigma}_1\right)\hfill & \hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_3{\Sigma}^{-1}{\Sigma}_1\right)\hfill \\ {}\hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_2{\Sigma}^{-1}{\Sigma}_1\right)\hfill & \hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_2{\Sigma}^{-1}{\Sigma}_2\right)\hfill & \hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_3{\Sigma}^{-1}{\Sigma}_2\right)\hfill \\ {}\hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_3{\Sigma}^{-1}{\Sigma}_1\right)\hfill & \hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_3{\Sigma}^{-1}{\Sigma}_2\right)\hfill & \hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_3{\Sigma}^{-1}{\Sigma}_3\right)\hfill \end{array}\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ40.gif)
![$$ F=E(H)=\frac{1}{2}\left[\begin{array}{ccc}\hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_1{\Sigma}^{-1}{\Sigma}_1\right)\hfill & \hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_2{\Sigma}^{-1}{\Sigma}_1\right)\hfill & \hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_3{\Sigma}^{-1}{\Sigma}_1\right)\hfill \\ {}\hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_2{\Sigma}^{-1}{\Sigma}_1\right)\hfill & \hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_2{\Sigma}^{-1}{\Sigma}_2\right)\hfill & \hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_3{\Sigma}^{-1}{\Sigma}_2\right)\hfill \\ {}\hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_3{\Sigma}^{-1}{\Sigma}_1\right)\hfill & \hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_3{\Sigma}^{-1}{\Sigma}_2\right)\hfill & \hfill {\it tr}\left({\Sigma}^{-1}{\Sigma}_3{\Sigma}^{-1}{\Sigma}_3\right)\hfill \end{array}\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ40.gif)
(3.40)
3.3 Iterative Trust Region Method for ML Estimation
NR method has the advantage of being simple and easy to implement. However, NR is not stable if the condition number of Hessian matrix is large, i.e., ill conditioned. To overcome this limitation, we need to introduce a damper factor to make the Hessian matrix invertible; this leads to trust region algorithm, i.e., Levenberg–Marquardt (LM) algorithm.
3.3.1 Levenberg–Marquardt (LM) Algorithm
Initially, LM algorithm provides a solution to the problem of nonlinear least squares estimation [23–25] and it has been applied in mixed model analysis [28, 29]. LM algorithm is more robust than NR method, which suggests that in many cases it finds a solution even if it starts very far off the final maximum. The idea of LM is to introduce a (nonnegative) damping factor λ to adjust the Hessian matrix at each iteration. For example, in the mixed model for group average in Eq. (3.26), we introduce a damper factor λ > 0 in the Hessian matrix, which leads to
![$$ {\left[\ \begin{array}{c}\hfill {\widehat{\sigma}}_{\mathrm{random}}^2\hfill \\ {}\hfill \widehat{\beta}\hfill \end{array}\ \ \right]}^{\left(k+1\right)}\ \ ={\left[\ \begin{array}{c}\hfill {\widehat{\sigma}}_{\mathrm{random}}^2\hfill \\ {}\hfill \widehat{\beta}\hfill \end{array}\ \right]}^{(k)}\ \ -{\left(H{\left(\widehat{\theta}\right)}^{{}^{(k)}}\ \ +\lambda \cdot \mathrm{diag}\left(H{\left(\widehat{\theta}\right)}\right)^{{}^{(k)}}\right)}^{-1}{\left[\begin{array}{c}\hfill {S}_1\left(\widehat{\theta}\right)\hfill \\ {}\hfill {S}_2\left(\widehat{\theta}\right)\hfill \end{array}\right]}^{(k)} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ41.gif)
where diag 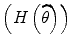 is diagonal element of Hessian matrix and λ > 0 is sufficiently large so that it can reduce the size of the
is diagonal element of Hessian matrix and λ > 0 is sufficiently large so that it can reduce the size of the 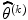 step and rotate it slightly in the direction of
step and rotate it slightly in the direction of 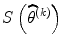 . Because we need to vary the LM parameter as the iteration progresses, this method is called trust region algorithm in numerical analysis [25, 26]. For the expectation trust region method, we need to replace Hessian matrix (e.g., Eq. (3.23)) with IM (e.g., Eq. (3.24)) for group average.
. Because we need to vary the LM parameter as the iteration progresses, this method is called trust region algorithm in numerical analysis [25, 26]. For the expectation trust region method, we need to replace Hessian matrix (e.g., Eq. (3.23)) with IM (e.g., Eq. (3.24)) for group average.
![$$ {\left[\ \begin{array}{c}\hfill {\widehat{\sigma}}_{\mathrm{random}}^2\hfill \\ {}\hfill \widehat{\beta}\hfill \end{array}\ \ \right]}^{\left(k+1\right)}\ \ ={\left[\ \begin{array}{c}\hfill {\widehat{\sigma}}_{\mathrm{random}}^2\hfill \\ {}\hfill \widehat{\beta}\hfill \end{array}\ \right]}^{(k)}\ \ -{\left(H{\left(\widehat{\theta}\right)}^{{}^{(k)}}\ \ +\lambda \cdot \mathrm{diag}\left(H{\left(\widehat{\theta}\right)}\right)^{{}^{(k)}}\right)}^{-1}{\left[\begin{array}{c}\hfill {S}_1\left(\widehat{\theta}\right)\hfill \\ {}\hfill {S}_2\left(\widehat{\theta}\right)\hfill \end{array}\right]}^{(k)} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ41.gif)
(3.41)
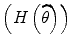 is diagonal element of Hessian matrix and λ > 0 is sufficiently large so that it can reduce the size of the
is diagonal element of Hessian matrix and λ > 0 is sufficiently large so that it can reduce the size of the 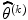 step and rotate it slightly in the direction of
step and rotate it slightly in the direction of 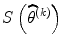 . Because we need to vary the LM parameter as the iteration progresses, this method is called trust region algorithm in numerical analysis [25, 26]. For the expectation trust region method, we need to replace Hessian matrix (e.g., Eq. (3.23)) with IM (e.g., Eq. (3.24)) for group average.
. Because we need to vary the LM parameter as the iteration progresses, this method is called trust region algorithm in numerical analysis [25, 26]. For the expectation trust region method, we need to replace Hessian matrix (e.g., Eq. (3.23)) with IM (e.g., Eq. (3.24)) for group average.Similarly, for different group comparison in Sect. 3.2.4, the LM algorithm for random effect variance estimation becomes
![$$ {\left[\begin{array}{c}\hfill {\sigma}_1^2\hfill \\ {}\hfill {\sigma}_{12}\hfill \\ {}\hfill {\sigma}_2^2\hfill \end{array}\right]}^{\left(k+1\right)}={\left[\begin{array}{c}\hfill {\sigma}_1^2\hfill \\ {}\hfill {\sigma}_{12}\hfill \\ {}\hfill {\sigma}_2^2\hfill \end{array}\right]}^{(k)}-{\left(H+\lambda \cdot \mathrm{diag}(H)\right)}^{-1(k)}{\left[\begin{array}{c}\hfill {S}_1\hfill \\ {}\hfill {S}_2\hfill \\ {}\hfill {S}_3\hfill \end{array}\right]}^{(k)} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ42.gif)
![$$ {\left[\begin{array}{c}\hfill {\sigma}_1^2\hfill \\ {}\hfill {\sigma}_{12}\hfill \\ {}\hfill {\sigma}_2^2\hfill \end{array}\right]}^{\left(k+1\right)}={\left[\begin{array}{c}\hfill {\sigma}_1^2\hfill \\ {}\hfill {\sigma}_{12}\hfill \\ {}\hfill {\sigma}_2^2\hfill \end{array}\right]}^{(k)}-{\left(H+\lambda \cdot \mathrm{diag}(H)\right)}^{-1(k)}{\left[\begin{array}{c}\hfill {S}_1\hfill \\ {}\hfill {S}_2\hfill \\ {}\hfill {S}_3\hfill \end{array}\right]}^{(k)} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ42.gif)
(3.42)
3.3.2 LM Algorithm Implementation
As other nonlinear optimization algorithm, the first step for applying the LM algorithm is to assign an initial value parameters vector θ = [σ 2 random,β]0T




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



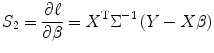
![$$ {H}_{11}=\frac{1}{2}\left[ tr\left({\Sigma}^{-1}{\Sigma}^{-1}\right)-2{\left(y- X\beta \right)}^{\mathrm{T}}{\left({\Sigma}^{-1}\right)}^3\left(y- X\beta \right)\right] $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ20.gif)
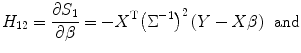
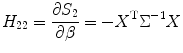
![$$ \begin{aligned}[b] {H}_{12}=\frac{\partial {S}_1}{\partial {\sigma}_{12}}=\frac{1}{2} & \left[ {\it tr}\left({\Sigma}^{-1}\left({\Sigma}_2\right){\Sigma}^{-1}\left({\Sigma}_1\right)\right)\right.\\[-3pt] & \quad \left.-{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}\left({\Sigma}_2\right){\Sigma}^{-1}\left({\Sigma}_1\right)\Sigma {}^{-1}\left(y- X\beta \right)\right.\\ & \quad \left.-{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}\left({\Sigma}_1\right){\Sigma}^{-1}\left({\Sigma}_2\right)\Sigma {}^{-1}\left(y- X\beta \right)\right]. \end{aligned} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ35.gif)
![$$ \begin{aligned}{H}_{13}=\frac{\partial {S}_1}{\partial {\sigma}_2^2} =\frac{1}{2}&\left[ \vphantom{} tr\left({\Sigma}^{-1}\left({\Sigma}_3\right){\Sigma}^{-1}\left({\Sigma}_1\right)\right)-{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}\left({\Sigma}_3\right){\Sigma}^{-1}\left({\Sigma}_1\right)\right.\\[-3pt] & \left.- {\Sigma}^{-1}\left(y- X\beta \right) {\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}\left({\Sigma}_1\right){\Sigma}^{-1}\left({\Sigma}_3\right){\Sigma}^{-1}\left(y- X\beta \right)\right]\end{aligned} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ36.gif)
![$$ \begin{aligned}[b] {H}_{22}=\frac{\partial {S}_2}{\partial {\sigma}_{12}}&=\frac{1}{2}\left[ {\it tr}\left({\Sigma}^{-1}\left({\Sigma}_2\right){\Sigma}^{-1}\left({\Sigma}_2\right)\right) \right.\\[-3pt] & \qquad\left. -2{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}\left({\Sigma}_2\right){\Sigma}^{-1}\left({\Sigma}_2\right){\Sigma}^{-1}\left(y- X\beta \right)\right] \end{aligned} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ37.gif)
![$$ \begin{aligned}{H}_{23} =\frac{\partial {S}_2}{\partial {\sigma}_2^2} =\frac{1}{2}&\left[ {\it tr}\left({\Sigma}^{-1}\left({\Sigma}_3\right){\Sigma}^{-1}\left({\Sigma}_2\right)\right)-{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}\left({\Sigma}_3\right){\Sigma}^{-1}\left({\Sigma}_2\right)\right.\\[-3pt] & \left. {\Sigma}^{-1}\left(y- X\beta \right) -{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}\left({\Sigma}_2\right){\Sigma}^{-1}\left({\Sigma}_3\right){\Sigma}^{-1}\left(y- X\beta \right)\right]\end{aligned} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ38.gif)
![$$ \begin{aligned}[b] {H}_{33}=\frac{\partial {S}_3}{\partial {\sigma}_2^2}=\frac{1}{2} & \left[ {\it tr}\left({\Sigma}^{-1}\left({\Sigma}_3\right){\Sigma}^{-1}\left({\Sigma}_3\right)\right)\right. \\[-3pt] & \left. -2{\left(y- X\beta \right)}^{\mathrm{T}}{\Sigma}^{-1}\left({\Sigma}_3\right){\Sigma}^{-1}\left({\Sigma}_3\right){\Sigma}^{-1}\left(y- X\beta \right)\right] \end{aligned} $$](/wp-content/uploads/2016/04/A317179_1_En_3_Chapter_Equ39.gif)