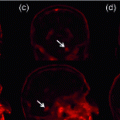
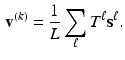Fig. 1.
Microscope images of Drosophila melanogaster imaginal discs with gene expression patterns (Color figure online).
A popular method which aligns images and simultaneously estimates a simple statistical shape model was proposed by E. Learned-Miller in [9] and is known as congealing. It considers the entropy of a simple, pixel-wise independent distribution as the objective function for searching the unknown transformations. This idea is indeed intuitive and appealing. Quite a few works were following it and have proposed different variants and generalisations of this approach [1, 5, 7, 10].
Besides from being intuitive and appealing, this idea raises several theoretical and practical questions. Firstly, entropy minimisation is not a commonly accepted estimator in mathematical statistics. Secondly, from the algorithmic point of view, one has to minimise a non convex function depending on many variables. Almost all methods that apply congealing solve the optimisation task by block-wise local coordinate descent without a guarantee to converge to a local minimum. And finally, from the conceptual view, we may wish to decouple the shape model from the signal domain and to formulate it in terms of segmentation labellings. This will require unsupervised estimation (learning).
In this paper we try to answer at least some of the raised questions. First, we show that the original congealing is in fact the DC-dual task (difference of convex functions) for a properly formulated Maximum Likelihood estimation task. This interpretation immediately leads to a different choice for the algorithm which is substantially simpler and faster than the known congealing algorithm.
The second contribution is to show how to generalise the task for models in which the shape is formulated in terms of segmentation labellings and is related to the signal domain via a parametric appearance model. We show how to estimate the parameters of the shape model together with the parameters of the appearance model and the collection of transformations given a set of object images. We call this generalisation unsupervised congealing.
In the experimental section we first apply the new, unsupervised congealing to artificially generated images. This allows to compare the results with the known ground truth. In the second, and main part of this section we apply the newly proposed method to the task of aligning and segmenting imaginal discs and compare it with a previously published approach [6].
2 Theory
In the first part of this section we will show that supervised congealing, as introduced in [9], is indeed the DC-dual of a Maximum Likelihood estimation task. To avoid overloading with technicalities like boundary effects, infinite dimensional function spaces etc., we consider a simple probabilistic model for binary images defined on a two dimensional discrete torus 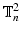 .
.
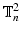 .
.2.1 Notations and Model
Let 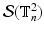 denote the set of all binary images
denote the set of all binary images 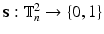 defined on the two dimensional discrete torus
defined on the two dimensional discrete torus 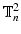 . We will denote the value of the image
. We will denote the value of the image 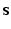 in a particular node
in a particular node 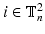 of the torus by
of the torus by 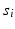 .
.
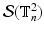 denote the set of all binary images
denote the set of all binary images 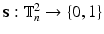 defined on the two dimensional discrete torus
defined on the two dimensional discrete torus 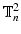 . We will denote the value of the image
. We will denote the value of the image 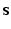 in a particular node
in a particular node 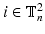 of the torus by
of the torus by 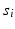 .
.Let us consider the following family of pixelwise independent probability distributions on 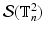
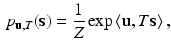
where 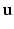 is a real valued field of parameters defined on
is a real valued field of parameters defined on 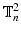 and
and 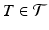 denotes an orthogonal linear transformation
denotes an orthogonal linear transformation 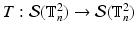 , for example rigid body transformations. Notice that the normalising factor Z is independent of T as a consequence. For the sake of simplicity we assume here that
, for example rigid body transformations. Notice that the normalising factor Z is independent of T as a consequence. For the sake of simplicity we assume here that 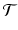 is the set of all discrete translations of the torus.
is the set of all discrete translations of the torus.
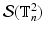
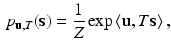
(1)
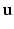 is a real valued field of parameters defined on
is a real valued field of parameters defined on 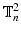 and
and 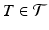 denotes an orthogonal linear transformation
denotes an orthogonal linear transformation 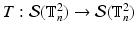 , for example rigid body transformations. Notice that the normalising factor Z is independent of T as a consequence. For the sake of simplicity we assume here that
, for example rigid body transformations. Notice that the normalising factor Z is independent of T as a consequence. For the sake of simplicity we assume here that 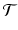 is the set of all discrete translations of the torus.
is the set of all discrete translations of the torus.Suppose now, that we are given a set of binary images 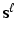 ,
, 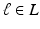 , each of them independently generated by one of the distributions
, each of them independently generated by one of the distributions 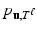 . All of them share the parameter vector
. All of them share the parameter vector 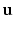 , but each of them has a different
, but each of them has a different 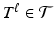 . Both, the vector
. Both, the vector 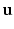 and the collection of transformations
and the collection of transformations 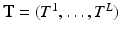 are unknown and should be estimated from the given sample of (binary) images.
are unknown and should be estimated from the given sample of (binary) images.
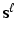 ,
, 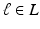 , each of them independently generated by one of the distributions
, each of them independently generated by one of the distributions 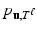 . All of them share the parameter vector
. All of them share the parameter vector  , but each of them has a different
, but each of them has a different 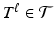 . Both, the vector
. Both, the vector 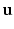 and the collection of transformations
and the collection of transformations 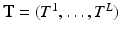 are unknown and should be estimated from the given sample of (binary) images.
are unknown and should be estimated from the given sample of (binary) images.2.2 DC-duality of MLE and Congealing
Applying the Maximum Likelihood Estimator (MLE) for this task, means to solve the following optimisation problem
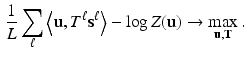
The normalisations factor (considered as a function of  ) is easy to compute
) is easy to compute
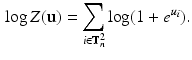
We may rewrite the optimisation task equivalently by
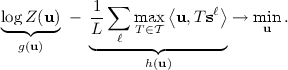
This is a DC program, because we have to minimise a difference of convex functions. Every DC program has a related DC dual program which has the same optimal value as the primal one
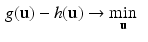
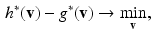
where for a given function g, 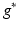 is its Fenchel conjugate defined by
is its Fenchel conjugate defined by
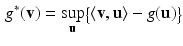
See e.g. [2, 3] for the theory of DC programs, duality and related algorithms.
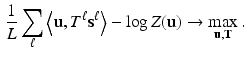
(2)
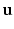 ) is easy to compute
) is easy to compute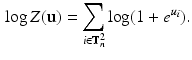
(3)
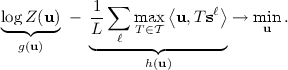
(4)
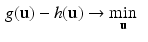
(5)
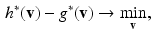
(6)
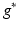 is its Fenchel conjugate defined by
is its Fenchel conjugate defined by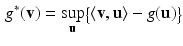
(7)
Let us have a closer look at the DC-dual program (6). It is easy to prove, that the Fenchel conjugate of 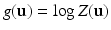 is the (negative) entropy
is the (negative) entropy
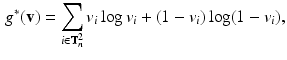
where we use the convention that 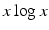 is zero if
is zero if 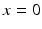 and is
and is 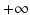 if x is negative. Let us compute the Fenchel conjugate of the function
if x is negative. Let us compute the Fenchel conjugate of the function 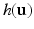
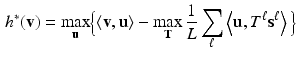
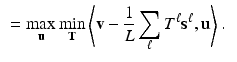
This problem has the form 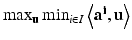 . Its value is either infinity if the origin does not lie in the convex hull of the vectors
. Its value is either infinity if the origin does not lie in the convex hull of the vectors 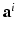 ,
, 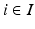 or zero in the opposite case. It follows from Gordan’s lemma (see e.g. [4]). Hence, we obtain
or zero in the opposite case. It follows from Gordan’s lemma (see e.g. [4]). Hence, we obtain 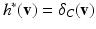 , where the indicator function
, where the indicator function 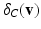 is 0 for
is 0 for 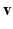 in C and
in C and 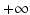 otherwise. The set C is the convex hull of all possible average images, i.e.
otherwise. The set C is the convex hull of all possible average images, i.e.
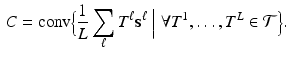
From all that we see that (6) requires to minimise the entropy (8) on the convex polytope C. Since the entropy is a concave function, the minimum is attained at an extremal point (vertex) of C. This in turn is precisely the task which congealing aims to solve. Hence, we proved the following theorem.
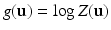 is the (negative) entropy
is the (negative) entropy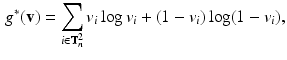
(8)
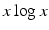 is zero if
is zero if 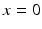 and is
and is 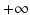 if x is negative. Let us compute the Fenchel conjugate of the function
if x is negative. Let us compute the Fenchel conjugate of the function 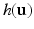
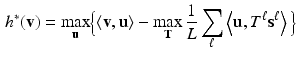
(9)
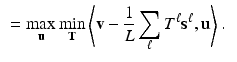
(10)
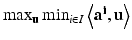 . Its value is either infinity if the origin does not lie in the convex hull of the vectors
. Its value is either infinity if the origin does not lie in the convex hull of the vectors 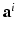 ,
, 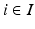 or zero in the opposite case. It follows from Gordan’s lemma (see e.g. [4]). Hence, we obtain
or zero in the opposite case. It follows from Gordan’s lemma (see e.g. [4]). Hence, we obtain 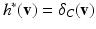 , where the indicator function
, where the indicator function 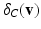 is 0 for
is 0 for 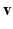 in C and
in C and 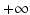 otherwise. The set C is the convex hull of all possible average images, i.e.
otherwise. The set C is the convex hull of all possible average images, i.e.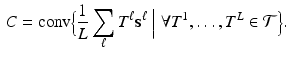
(11)
Theorem 1
For the model family (1) and any (finite) set 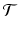 of orthogonal transformations
of orthogonal transformations 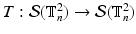 , congealing and MLE are DC-duals of each other. In particular, their optimal values are equal.
, congealing and MLE are DC-duals of each other. In particular, their optimal values are equal.
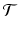 of orthogonal transformations
of orthogonal transformations 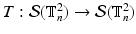 , congealing and MLE are DC-duals of each other. In particular, their optimal values are equal.
, congealing and MLE are DC-duals of each other. In particular, their optimal values are equal.2.3 A DC-algorithm
Congealing aims at solving the dual task (6) directly, i.e. to minimise the entropy (8) as a function of 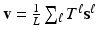 w.r.t. to all possible collections of transformations
w.r.t. to all possible collections of transformations 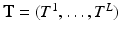 . This is usually done by block-wise local coordinate descent. Given the current
. This is usually done by block-wise local coordinate descent. Given the current 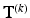 , the algorithm tries to improve the entropy by sequentially probing local changes for each
, the algorithm tries to improve the entropy by sequentially probing local changes for each 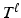 . Such an approach lacks a guarantee to converge to a local minimum.
. Such an approach lacks a guarantee to converge to a local minimum.
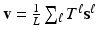 w.r.t. to all possible collections of transformations
w.r.t. to all possible collections of transformations 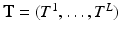 . This is usually done by block-wise local coordinate descent. Given the current
. This is usually done by block-wise local coordinate descent. Given the current 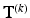 , the algorithm tries to improve the entropy by sequentially probing local changes for each
, the algorithm tries to improve the entropy by sequentially probing local changes for each 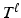 . Such an approach lacks a guarantee to converge to a local minimum.
. Such an approach lacks a guarantee to converge to a local minimum.Another option is to apply a DC algorithm. This type of algorithm aims at solving the primal and the dual task simultaneously, by constructing a pair of sequences 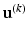 ,
, 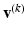 in an alternating way
in an alternating way
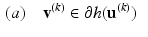
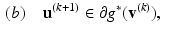
where 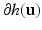 denotes the sub-differential of a convex function h at point
denotes the sub-differential of a convex function h at point 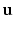 . In the case being considered, the algorithm reads as follows. Choose an initial
. In the case being considered, the algorithm reads as follows. Choose an initial 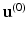 and repeat applying the following two steps until convergence
and repeat applying the following two steps until convergence
Get Clinical Tree app for offline access
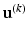 ,
, 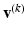 in an alternating way
in an alternating way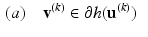
(12)
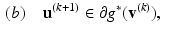
(13)
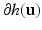 denotes the sub-differential of a convex function h at point
denotes the sub-differential of a convex function h at point 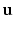 . In the case being considered, the algorithm reads as follows. Choose an initial
. In the case being considered, the algorithm reads as follows. Choose an initial 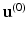 and repeat applying the following two steps until convergence
and repeat applying the following two steps until convergence
(a) Find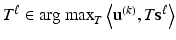 for each image
for each image 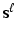 independently. Set
independently. Set