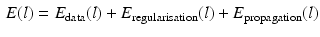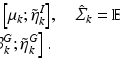.
1 Introduction
In recent years, major efforts have been undertaken towards building large medical image databases, e.g. in population studies. As the wealth of data increases, automated segmentation of images becomes crucial while manually annotating them becomes prohibitive. In particular, robust and accurate segmentation techniques relying on minimal manual input become increasingly desirable.
Atlas-based segmentation has proven to be a successful and robust tool for a number of applications. Many of these techniques [1, 2, 7] rely on label propagation from multiple suitable atlases after non-linear registration to a target image. The target segmentation can be formed by label fusion of the propagated labels, for example by applying a majority vote rule [1, 7] or another combination strategy such as a weighted average based on global or local similarity measures between the target and atlas images [2]. Other combination strategies include STAPLE [20], where label fusion weights are estimated with an Expectation-Minimisation algorithm, or Joint Label Fusion [19], where correlations among atlases are taken into account. To account for high local anatomical variability between images, patch-based segmentation [5, 17] has been introduced, where the label fusion step employs a non-local weighted average of voxel labels in a small neighbourhood of the atlas images, with weights based on the similarities of patches centred on the compared voxels. Considerable improvements to results obtained with label propagation can be achieved by using the label propagation results as prior probabilities in subsequent refinement steps, combining them with regularisation terms and an intensity model in a Markov Random Field (MRF) formulation [11–13]. It has been shown that in general, segmentation accuracy decreases when fewer [7] or less suitable [1] atlases are used.
All of the above methods rely on the availability of fully annotated atlas data. However, segmentation methods requiring only a proportion of each atlas image to be labelled (while no knowledge is necessary about the remaining voxels) could reduce the workload of raters who manually label these atlases. [9] proposed an extension to STAPLE [20] which, to our knowledge, is the only existing multi-atlas segmentation method that uses partially annotated atlas data. However, partial annotations have been used in the context of interactive segmentation. In [4], regions of an image were manually labelled to enable automated segmentation of the remaining image. In particular, an MRF energy function [10] was formulated on a graph constructed on the regular image grid in which annotated voxels are connected to virtual terminal nodes with infinite weights. The MRF energy minimisation problem was efficiently solved by finding a min-cut/max-flow on the graph with graph-cuts [4]. An iterative graph-cuts approach [16] has been proposed to reduce user interaction compared to [4].
Some applications of graph-cuts employ MRF energy functions that have been formulated for labelling on graphs connecting more than one image. Recently, [6] applied graph-cuts for tumor segmentation based on PET and CT image pairs by minimising an MRF energy function which penalises segmentation differences between a PET and CT image of the same subject. [15] proposed a prostate segmentation algorithm in which multiple 2D slices were extracted from a 3D image at different angles. Exploiting axial symmetry, the 2D slices were simultaneously segmented using a max-flow algorithm which penalised segmentation differences between slices at similar angles. The max-flow algorithm they used is an extension of the recently proposed Continuous Max-Flow (CMF), which solves a continuous counterpart to the discrete min-cut/max-flow problem [21]. CMF can be computed using a reliable, highly parallelisable multiplier-based algorithm with guaranteed convergence, making it suitable for the optimisation of large labelling problems in parallel computing environments.
Combining aspects of multi-atlas segmentation with recent developments in min-cut/max-flow methods [15, 21], and with the goal of successfully exploiting partially labelled images for segmentation, we propose a segmentation framework incorporating three novel contributions:
1.
We revisit the labelling problem in existing multi-atlas segmentation methods and express the solution in terms of labelling a graph which connects the target and atlas images. We formulate an MRF energy function on this graph and show analytically that its solution is equivalent to existing multi-atlas segmentation methods [2, 7]. We then show how spatial regularisation and intensity models [11] can be readily incorporated in the proposed formulation.
2.
We provide a generalisation of the Continuous Max-Flow algorithm which can efficiently minimise energy functions on graphs connecting multiple images. The proposed generalised CMF is applied to the graph labelling problem formulated here. However, as it is highly parallelisable, its scalability to large graphs could make it useful for solving large-scale MRF frameworks beyond the scope of this work.
3.
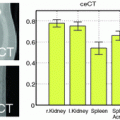
We show that the proposed method can provide automated segmentations using partially annotated atlas data. To evaluate the method, we apply it to hippocampal segmentation in 202 Magnetic Resonance (MR) images of the ADNI database and investigate its performance under varying proportions of labelled voxels per atlas image.
2 Method
In the following sections, we revisit multi-atlas segmentation (Sect. 2.1) and show how it can be viewed as a labelling problem on a graph connecting atlases and the target image (Sect. 2.2). In Sect. 2.3 we discuss extensions to the proposed MRF energy function to integrate label propagation, regularisation, as well as intensity models into a single comprehensive framework. Furthermore, we show how the proposed methodology can be applied to segmentation problems where only partially annotated atlas data are available (Sect. 2.4). The optimisation of the proposed energy function is discussed in Sect. 2.5.
2.1 Multi-atlas Label Propagation
For multi-atlas segmentation [2, 7] using R images, all atlas images  are registered to the target image i. For convenience we assume
are registered to the target image i. For convenience we assume 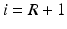 . The label maps
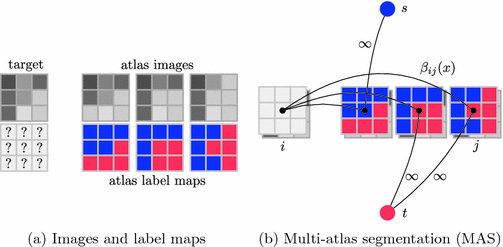
. The label maps 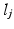 associated with the atlas images j are then propagated to the target. Figure 1a shows an example atlas set with corresponding label maps, and an unlabelled target image. Each voxel
associated with the atlas images j are then propagated to the target. Figure 1a shows an example atlas set with corresponding label maps, and an unlabelled target image. Each voxel 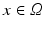 in the target image i is labelled using some combination strategy, e.g. a weighted average of atlas labels
in the target image i is labelled using some combination strategy, e.g. a weighted average of atlas labels 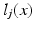 :
:
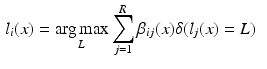
Here 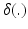 is an indicator function. The weights
is an indicator function. The weights 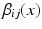 can be uniform (which is equivalent to a majority vote rule) or based on global or local similarity measures between images i and j. Suitable measures were investigated in [2].
can be uniform (which is equivalent to a majority vote rule) or based on global or local similarity measures between images i and j. Suitable measures were investigated in [2].
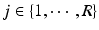 are registered to the target image i. For convenience we assume
are registered to the target image i. For convenience we assume 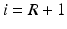 . The label maps
. The label maps 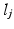 associated with the atlas images j are then propagated to the target. Figure 1a shows an example atlas set with corresponding label maps, and an unlabelled target image. Each voxel
associated with the atlas images j are then propagated to the target. Figure 1a shows an example atlas set with corresponding label maps, and an unlabelled target image. Each voxel 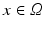 in the target image i is labelled using some combination strategy, e.g. a weighted average of atlas labels
in the target image i is labelled using some combination strategy, e.g. a weighted average of atlas labels 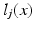 :
: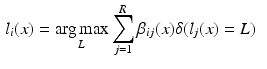
(1)
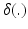 is an indicator function. The weights
is an indicator function. The weights 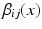 can be uniform (which is equivalent to a majority vote rule) or based on global or local similarity measures between images i and j. Suitable measures were investigated in [2].
can be uniform (which is equivalent to a majority vote rule) or based on global or local similarity measures between images i and j. Suitable measures were investigated in [2].
Fig. 1.
(a) An example dataset with an unlabelled target image on the left, atlas images and corresponding manual annotations (blue and red depict different labels) on the right. (b) In MAS, each voxel x in target image i is labelled by label propagation from atlases 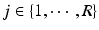 with fusion weights
with fusion weights 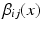 . This can also be interpreted as a graph labelling problem, where atlas voxels are connected to the terminal nodes with infinitely weighted edges (Color figure online).
. This can also be interpreted as a graph labelling problem, where atlas voxels are connected to the terminal nodes with infinitely weighted edges (Color figure online).
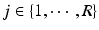 with fusion weights
with fusion weights 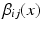 . This can also be interpreted as a graph labelling problem, where atlas voxels are connected to the terminal nodes with infinitely weighted edges (Color figure online).
. This can also be interpreted as a graph labelling problem, where atlas voxels are connected to the terminal nodes with infinitely weighted edges (Color figure online).2.2 Reformulation as a Graph Labelling Problem
As an alternative perspective, we can construct a graph to model the relationship of shared information between the atlases and the target. According to the above labelling scenario, this graph connects each voxel x in the target image i to the corresponding voxels in the atlas images j with an edge weighted by 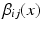 . Figure 1b visualises this configuration. To find a labelling on the graph, we can formulate a potential function V that penalises conflicting labels in voxels connected by a high weight
. Figure 1b visualises this configuration. To find a labelling on the graph, we can formulate a potential function V that penalises conflicting labels in voxels connected by a high weight 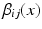 , e.g.
, e.g.
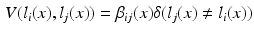
This assigns a high penalty when the target and atlas labels differ and the atlas is considered similar to the target i, as defined by the similarity measure 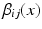 . In the case of a majority vote, the weights are uniform, e.g.
. In the case of a majority vote, the weights are uniform, e.g. 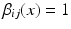 . The cost for labelling an individual voxel x in image i can then be calculated as follows:
. The cost for labelling an individual voxel x in image i can then be calculated as follows:
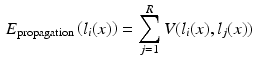
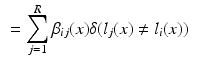
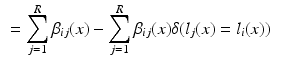
In this formulation the labels in the atlases are fixed. This is achieved by assigning infinite unary potentials to the atlas voxels (visualised as infinitely weighted edges to the terminal nodes in Fig. 1b for the binary case). Voxels in the target image are assumed to be conditionally independent since spatially neighbouring voxels in the target image are not connected in the graph (in contrast to the setting for regularisation in many vision problems [10]). The optimal label can therefore be found by minimising 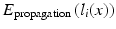 independently for all voxels:
independently for all voxels:
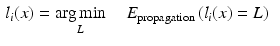
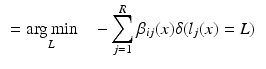
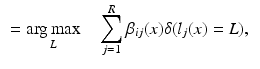
which leads to the same result as the vote rule in Eq. 1. This demonstrates that multi-atlas segmentation can be expressed in terms of a graph optimisation problem. It is important to note that patch-based segmentation (PBS [5, 17]) can also be expressed in this framework. In this case we can use a slightly different graph structure as the label fusion step in PBS takes into account multiple voxels in a neighbourhood of x in each atlas instead of just one voxel at location x.
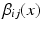 . Figure 1b visualises this configuration. To find a labelling on the graph, we can formulate a potential function V that penalises conflicting labels in voxels connected by a high weight
. Figure 1b visualises this configuration. To find a labelling on the graph, we can formulate a potential function V that penalises conflicting labels in voxels connected by a high weight 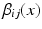 , e.g.
, e.g.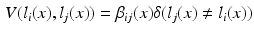
(2)
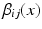 . In the case of a majority vote, the weights are uniform, e.g.
. In the case of a majority vote, the weights are uniform, e.g. 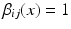 . The cost for labelling an individual voxel x in image i can then be calculated as follows:
. The cost for labelling an individual voxel x in image i can then be calculated as follows: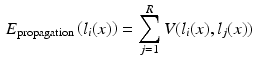
(3)
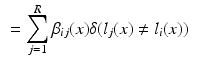
(4)
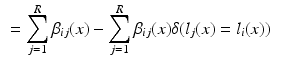
(5)
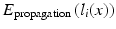 independently for all voxels:
independently for all voxels: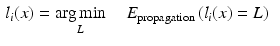
(6)
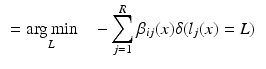
(7)
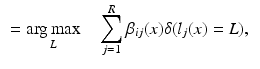
(8)
While this alternative problem formulation does not provide any immediate benefits over traditional multi-atlas segmentation in itself (because it is equivalent), it has two advantages: (1) it allows easy integration of additional components and therefore provides a unifying reformulation for existing multi-atlas segmentation methods, as shown in Sect. 2.3 and (2) the graphical approach extends to segmentation using partially annotated atlases (Sect. 2.4).
2.3 Unified Label Propagation Framework
As we are interpreting the whole dataset, comprising target and atlas images, as one graph satisfying Markov properties, we can assign unary potentials (data terms) to each voxel in all images, and pairwise potentials to each pair of voxels [10]. In the previous section, we proposed assigning pairwise potentials between target and atlas voxels for label propagation. In addition, we assigned infinite unary potentials to the atlas voxels since their labels are fixed. It is important to note that a data term can be specified for the target image as well, using prior probabilities, intensity models of the data, or a combination of both. Lastly, we can incorporate spatial regularisation with pairwise potentials between adjacent voxels within an image. The propagation, data, and regularisation terms can be combined to a comprehensive labelling energy function on the whole graph: