averaged over the whole data set.
1 Introduction
Due to reduced physical activity and modern office jobs that require prolonged sitting during work hours, pathological conditions affecting the spine have become a growing problem of modern society. As most spinal pathologies are related to vertebrae conditions, the development of methods for accurate and objective vertebrae segmentation in medical images represents an important and challenging research area. While manual segmentation of vertebrae is tedious and too time consuming to be used in clinical practice, automatic segmentation may provide means for a fast and objective analysis of vertebral condition. A current state of the art method for detecting, identifying and segmenting vertebrae in computed tomography (CT) images is proposed by Klinder et al. [5]. The method is based on a complex and computationally demanding alignment of statistical shape models to the vertebrae in the image. Using the deformable surface model and training an edge detector to bone structure, Ma et al. [6] segment and identify the thoracic vertebrae in CT images. In the work of Kadoury et al. [4], the global shape representation of individual vertebrae in the image is captured with a non-linear low-dimensional manifold of its mesh representation, while local vertebral appearance is captured from neighborhoods in the manifold once the overall representation converges during the segmentation process. Ibragimov et al. [3] used transportation theory to build their landmark-based shape representations of vertebrae and game theory to align the model to a specific vertebra in 3D CT images. In this paper, we propose a method for vertebrae segmentation in 3D CT images based on a convex variational framework. In contrast to the previously proposed methods that use sophisticated vertebral models, our segmentation method incorporates only a mean shape model of vertebrae initialized in the center of the vertebral body.
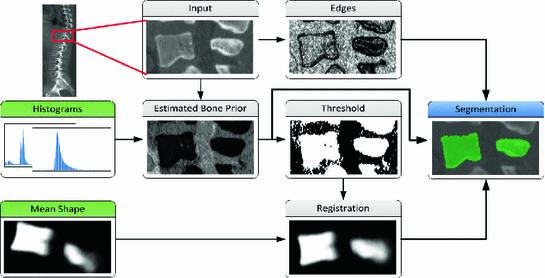

Fig. 1
Overview of our proposed algorithm. Green boxes represent a priori information obtained from training images. Bold arrows indicate parts that are included in the variational segmentation algorithm (color in online)
2 Methods
Our vertebrae segmentation algorithm is based on two representations of a priori information, a mean shape model and a bone probability map obtained from intensity information of the input vertebra image. The main steps of our algorithm are illustrated in Fig. 1. Firstly, an intensity based prior map of the bone is estimated by comparing the intensity values to trained bone and soft tissue histograms. This resembles our learned bone prior. The vertebral mean shape is then registered to the thresholded bone prior map to obtain the orientation of the individual vertebrae. This information is used to formulate a total variation (TV) based active contour segmentation problem, which combines the registered mean shape and the bone prior, and additionally incorporates edge information.
2.1 Mean Shape Model
The vertebral mean shape model 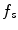 is calculated separately for three groups of vertebrae to account for variation in shape along the spine: T01–T06, T07–T12, L01–L05. Ground truth segmentations of vertebrae are registered to an arbitrary reference vertebra using an intensity-based registration with a similarity transformation and normalized cross correlation as similarity measure. The vertebral mean shape model is obtained by averaging the registered binary images of the ground truth segmented vertebrae. This step leads to a voxelwise probability for being part of the mean shape. To meet the requirements of the TV optimization framework [10], the obtained values in the probability image are inverted such that negative values represent the mean shape vertebral region and values close to one the non-vertebral region.
is calculated separately for three groups of vertebrae to account for variation in shape along the spine: T01–T06, T07–T12, L01–L05. Ground truth segmentations of vertebrae are registered to an arbitrary reference vertebra using an intensity-based registration with a similarity transformation and normalized cross correlation as similarity measure. The vertebral mean shape model is obtained by averaging the registered binary images of the ground truth segmented vertebrae. This step leads to a voxelwise probability for being part of the mean shape. To meet the requirements of the TV optimization framework [10], the obtained values in the probability image are inverted such that negative values represent the mean shape vertebral region and values close to one the non-vertebral region.
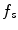 is calculated separately for three groups of vertebrae to account for variation in shape along the spine: T01–T06, T07–T12, L01–L05. Ground truth segmentations of vertebrae are registered to an arbitrary reference vertebra using an intensity-based registration with a similarity transformation and normalized cross correlation as similarity measure. The vertebral mean shape model is obtained by averaging the registered binary images of the ground truth segmented vertebrae. This step leads to a voxelwise probability for being part of the mean shape. To meet the requirements of the TV optimization framework [10], the obtained values in the probability image are inverted such that negative values represent the mean shape vertebral region and values close to one the non-vertebral region.
is calculated separately for three groups of vertebrae to account for variation in shape along the spine: T01–T06, T07–T12, L01–L05. Ground truth segmentations of vertebrae are registered to an arbitrary reference vertebra using an intensity-based registration with a similarity transformation and normalized cross correlation as similarity measure. The vertebral mean shape model is obtained by averaging the registered binary images of the ground truth segmented vertebrae. This step leads to a voxelwise probability for being part of the mean shape. To meet the requirements of the TV optimization framework [10], the obtained values in the probability image are inverted such that negative values represent the mean shape vertebral region and values close to one the non-vertebral region.2.2 Bone Prior Map
The bone prior map 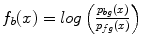 is calculated as the log likelihood ratio between the probability that a voxel
is calculated as the log likelihood ratio between the probability that a voxel 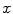 belongs to the bone distribution
belongs to the bone distribution 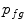 and the probability that it belongs to the soft tissue distribution
and the probability that it belongs to the soft tissue distribution 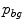 . The bone and soft tissue distributions are obtained from the training data set by estimating normalized mean foreground and background histograms of the intensity values using the ground truth segmentations. A coarse segmentation of the bone in the input image is achieved by thresholding the inverted bone map. We select a threshold value of
. The bone and soft tissue distributions are obtained from the training data set by estimating normalized mean foreground and background histograms of the intensity values using the ground truth segmentations. A coarse segmentation of the bone in the input image is achieved by thresholding the inverted bone map. We select a threshold value of 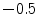 to ensure that trabecular bones are included in the segmented bone region, since their image intensities might be close to soft tissue.
to ensure that trabecular bones are included in the segmented bone region, since their image intensities might be close to soft tissue.
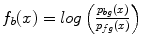 is calculated as the log likelihood ratio between the probability that a voxel
is calculated as the log likelihood ratio between the probability that a voxel 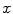 belongs to the bone distribution
belongs to the bone distribution 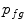 and the probability that it belongs to the soft tissue distribution
and the probability that it belongs to the soft tissue distribution 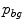 . The bone and soft tissue distributions are obtained from the training data set by estimating normalized mean foreground and background histograms of the intensity values using the ground truth segmentations. A coarse segmentation of the bone in the input image is achieved by thresholding the inverted bone map. We select a threshold value of
. The bone and soft tissue distributions are obtained from the training data set by estimating normalized mean foreground and background histograms of the intensity values using the ground truth segmentations. A coarse segmentation of the bone in the input image is achieved by thresholding the inverted bone map. We select a threshold value of 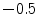 to ensure that trabecular bones are included in the segmented bone region, since their image intensities might be close to soft tissue.
to ensure that trabecular bones are included in the segmented bone region, since their image intensities might be close to soft tissue.2.3 Total Variation Segmentation
To obtain the segmented vertebra 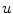 , the following non-smooth energy functional
, the following non-smooth energy functional 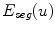 is minimized using the first order primal-dual algorithm from [1]:
is minimized using the first order primal-dual algorithm from [1]:
![$$\begin{aligned} \min \limits _{u\in [0,1]} E_{ seg}(u) = \min \limits _{u\in [0,1]} {{\mathrm{TV}}}_ { g,\,aniso}\;+\;\lambda _1 \int \limits _{\varOmega }uf_s \, dx+ \lambda _2 \int \limits _{\varOmega }uf_b \, dx \end{aligned}$$](/wp-content/uploads/2016/10/A331518_1_En_20_Chapter_Equ1.gif)
where 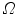 denotes the image domain. The trade-off between the vertebral mean shape model, bone prior map and image edge influence is regularized by the parameters
denotes the image domain. The trade-off between the vertebral mean shape model, bone prior map and image edge influence is regularized by the parameters 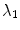 and
and 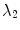 . The term
. The term 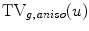 is the anisotropic
is the anisotropic 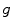 -weighted TV norm [7], using a structure tensor
-weighted TV norm [7], using a structure tensor 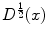 as proposed by [9], incorporating both edge magnitude and edge direction to be able to segment elongated structures:
as proposed by [9], incorporating both edge magnitude and edge direction to be able to segment elongated structures:
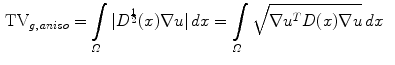
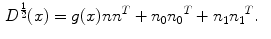
Here, 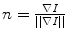 is the normalized image gradient,
is the normalized image gradient,  denotes an arbitrary vector in the tangent plane defined by
denotes an arbitrary vector in the tangent plane defined by 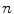 , and
, and 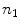 is the cross product between
is the cross product between 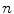 and
and 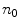 . The edge function
. The edge function 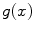 is defined as
is defined as
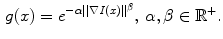
During minimization of the energy  , the segmentation
, the segmentation  tends to be foreground, if
tends to be foreground, if 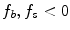 and background, if
and background, if ![$$f_b,f_s >0$$” src=”/wp-content/uploads/2016/10/A331518_1_En_20_Chapter_IEq26.gif”></SPAN>. If <SPAN id=IEq27 class=InlineEquation><IMG alt=$$f_b,f_s$$ src=]() equal zero, the pure TV energy is minimized, thus seeking for a segmentation surface with minimal surface area. The final segmentation is achieved by thresholding the segmentation
equal zero, the pure TV energy is minimized, thus seeking for a segmentation surface with minimal surface area. The final segmentation is achieved by thresholding the segmentation 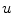 between 0 and 1.
between 0 and 1.
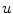 , the following non-smooth energy functional
, the following non-smooth energy functional 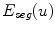 is minimized using the first order primal-dual algorithm from [1]:
is minimized using the first order primal-dual algorithm from [1]:![$$\begin{aligned} \min \limits _{u\in [0,1]} E_{ seg}(u) = \min \limits _{u\in [0,1]} {{\mathrm{TV}}}_ { g,\,aniso}\;+\;\lambda _1 \int \limits _{\varOmega }uf_s \, dx+ \lambda _2 \int \limits _{\varOmega }uf_b \, dx \end{aligned}$$](/wp-content/uploads/2016/10/A331518_1_En_20_Chapter_Equ1.gif)
(1)
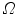 denotes the image domain. The trade-off between the vertebral mean shape model, bone prior map and image edge influence is regularized by the parameters
denotes the image domain. The trade-off between the vertebral mean shape model, bone prior map and image edge influence is regularized by the parameters 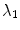 and
and 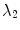 . The term
. The term 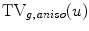 is the anisotropic
is the anisotropic 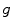 -weighted TV norm [7], using a structure tensor
-weighted TV norm [7], using a structure tensor 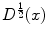 as proposed by [9], incorporating both edge magnitude and edge direction to be able to segment elongated structures:
as proposed by [9], incorporating both edge magnitude and edge direction to be able to segment elongated structures: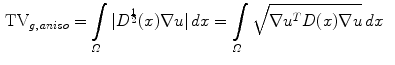
(2)
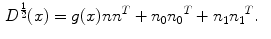
(3)
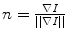 is the normalized image gradient,
is the normalized image gradient, 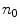 denotes an arbitrary vector in the tangent plane defined by
denotes an arbitrary vector in the tangent plane defined by 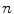 , and
, and 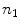 is the cross product between
is the cross product between 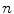 and
and 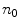 . The edge function
. The edge function 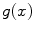 is defined as
is defined as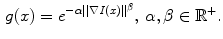
(4)
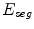 , the segmentation
, the segmentation 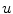 tends to be foreground, if
tends to be foreground, if 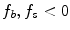 and background, if
and background, if 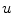 between 0 and 1.
between 0 and 1.3 Experimental Setup
We evaluated our method on the volumetric CT data sets provided for the CSI spine and vertebrae segmentation challenge [11]. The data consists of ten training images and the corresponding ground truth segmentations. The performance of our algorithm was evaluated by a leave-one-out cross validation, i.e., we report average performance over ten experiments.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree