denote the intensity non uniformity corrected image [8] with intensities in the normalized intensity space ![$$\mathcal {I}=[0,1]$$](/wp-content/uploads/2016/10/A331518_1_En_10_Chapter_IEq2.gif) , where
, where 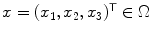 are the coordinates in the continuous image domain
are the coordinates in the continuous image domain  Throughout the whole section, we furthermore assume that the tubular structure of interest is roughly oriented parallel to the
Throughout the whole section, we furthermore assume that the tubular structure of interest is roughly oriented parallel to the  axis. Figuring out the orientation should be straightforward for most clinical applications, as the subject’s orientation with respect to the image can be determined from the image’s meta data for most clinical imaging modalities.
axis. Figuring out the orientation should be straightforward for most clinical applications, as the subject’s orientation with respect to the image can be determined from the image’s meta data for most clinical imaging modalities.
Original max-flow formulation. A general formulation for the continuous max-flow problem with spatial flow  , source flow
, source flow  , sink flow
, sink flow  , and corresponding flow capacities
, and corresponding flow capacities 
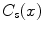 ,
, 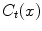 is stated by Yuan et al. [6] as
is stated by Yuan et al. [6] as

subject to the flow capacity constraints

and the flow conservation constraint

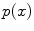 , source flow
, source flow  , sink flow
, sink flow  , and corresponding flow capacities
, and corresponding flow capacities 
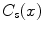 ,
, 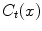 is stated by Yuan et al. [6] as
is stated by Yuan et al. [6] as
(1)

(2)

(3)
2.1 Cross-Sectional Similarity Prior
Following our goal to impose a cross-sectional similarity prior on the segmentation, we split the spatial flow  into an in-slice component
into an in-slice component  and a through-slice component
and a through-slice component 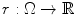 with respect to slices that lie perpendicular to the
with respect to slices that lie perpendicular to the 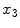 axis (see Fig. 1a). The resulting continuous max-flow problem can then be written as follows:
axis (see Fig. 1a). The resulting continuous max-flow problem can then be written as follows:

subject to the new flow capacity constraints

and the new flow conservation constraint

where  denotes the divergence of
denotes the divergence of 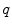 perpendicular to the
perpendicular to the 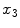 axis and
axis and 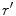 denotes the derivative of
denotes the derivative of  along the
along the 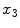 axis.
axis.

 into an in-slice component
into an in-slice component  and a through-slice component
and a through-slice component 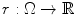 with respect to slices that lie perpendicular to the
with respect to slices that lie perpendicular to the 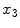 axis (see Fig. 1a). The resulting continuous max-flow problem can then be written as follows:
axis (see Fig. 1a). The resulting continuous max-flow problem can then be written as follows:
(4)

(5)

(6)
 denotes the divergence of
denotes the divergence of 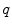 perpendicular to the
perpendicular to the 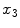 axis and
axis and 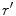 denotes the derivative of
denotes the derivative of  along the
along the 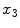 axis.
axis.
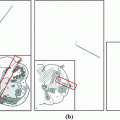
Fig. 1
Method overview. a Proposed flow configuration: the spatial flow is split into an in-slice component 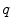 , perpendicular to the axis along which the tubular structure is oriented, and a through-slice component
, perpendicular to the axis along which the tubular structure is oriented, and a through-slice component 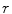 , parallel to the axis. b Sample sagittal slice of one of the images used for evaluation. c Segmentation result. d Surface reconstruction with cutting planes for volume measurement
, parallel to the axis. b Sample sagittal slice of one of the images used for evaluation. c Segmentation result. d Surface reconstruction with cutting planes for volume measurement
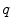 , perpendicular to the axis along which the tubular structure is oriented, and a through-slice component
, perpendicular to the axis along which the tubular structure is oriented, and a through-slice component 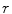 , parallel to the axis. b Sample sagittal slice of one of the images used for evaluation. c Segmentation result. d Surface reconstruction with cutting planes for volume measurement
, parallel to the axis. b Sample sagittal slice of one of the images used for evaluation. c Segmentation result. d Surface reconstruction with cutting planes for volume measurementThe flow formulation now possesses the desired property of having the spatial flow capacity  of [6] represented by two separate terms, namely the in-slice flow capacity
of [6] represented by two separate terms, namely the in-slice flow capacity 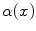 and the through-slice flow capacity
and the through-slice flow capacity  . The latter capacity,
. The latter capacity,  , represents the cross-sectional similarity prior that allows for precise control over the through-slice flow behavior: For example, we may choose an edge-based cost function for
, represents the cross-sectional similarity prior that allows for precise control over the through-slice flow behavior: For example, we may choose an edge-based cost function for  that drives the segmentation towards edges in
that drives the segmentation towards edges in 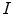 , while setting
, while setting  to enforce constant similarity throughout all slices. Or we may calculate
to enforce constant similarity throughout all slices. Or we may calculate  as a slice wise cost-function that, for each slice, adjusts the similarity prior to the in-slice noise level (reinforcing the similarity prior if the noise level is high and relaxing it if the noise level is low). Other combinations are possible, of course: note that both
as a slice wise cost-function that, for each slice, adjusts the similarity prior to the in-slice noise level (reinforcing the similarity prior if the noise level is high and relaxing it if the noise level is low). Other combinations are possible, of course: note that both  and
and  may be formulated pointwise.
may be formulated pointwise.
 of [6] represented by two separate terms, namely the in-slice flow capacity
of [6] represented by two separate terms, namely the in-slice flow capacity 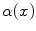 and the through-slice flow capacity
and the through-slice flow capacity  . The latter capacity,
. The latter capacity,  , represents the cross-sectional similarity prior that allows for precise control over the through-slice flow behavior: For example, we may choose an edge-based cost function for
, represents the cross-sectional similarity prior that allows for precise control over the through-slice flow behavior: For example, we may choose an edge-based cost function for  that drives the segmentation towards edges in
that drives the segmentation towards edges in 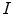 , while setting
, while setting  to enforce constant similarity throughout all slices. Or we may calculate
to enforce constant similarity throughout all slices. Or we may calculate  as a slice wise cost-function that, for each slice, adjusts the similarity prior to the in-slice noise level (reinforcing the similarity prior if the noise level is high and relaxing it if the noise level is low). Other combinations are possible, of course: note that both
as a slice wise cost-function that, for each slice, adjusts the similarity prior to the in-slice noise level (reinforcing the similarity prior if the noise level is high and relaxing it if the noise level is low). Other combinations are possible, of course: note that both  and
and  may be formulated pointwise.
may be formulated pointwise.Dual formulation. Introducing the Lagrange multiplier  and following the steps in [6], the max-flow problem can be reformulated as the equivalent primal-dual model
and following the steps in [6], the max-flow problem can be reformulated as the equivalent primal-dual model

subject to the capacity constraints (5). The equivalent dual model representing a relaxed min-cut problem then becomes
![$$\begin{aligned} \min _{u\in [0,1]}E(u)\mathbin {:=}\int \limits _{\Omega }\left\{ (1-u)C_{s}+uC_{t}+\alpha |{{\mathrm{\nabla _{{12}}}}}u|+\beta |u^{\prime }|\right\} {\mathrm{{d}}}{x}. \end{aligned}$$](/wp-content/uploads/2016/10/A331518_1_En_10_Chapter_Equ8.gif)
Here, 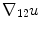 denotes the in-slice gradient and
denotes the in-slice gradient and 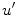 denotes the through-slice derivative of
denotes the through-slice derivative of  with respect to the
with respect to the  axis, similar to the definitions of
axis, similar to the definitions of  and
and  above. It can be shown that each level set function
above. It can be shown that each level set function ![$$u^{\ell }(x),\,\ell \in (0,1]$$](/wp-content/uploads/2016/10/A331518_1_En_10_Chapter_IEq41.gif) given by
given by
![$$\begin{aligned} u^{\ell }(x)\mathbin {:=}{\left\{ \begin{array}{ll} 1, &{} u^{*}(x)>\ell \\ 0, &{} u^{*}(x)\le \ell \end{array}\right. }\quad {\text {with}}\quad u^{*}\mathbin {:=}\mathop {\mathrm{{argmin}}}\limits _{u}E(u) \end{aligned}$$” src=”/wp-content/uploads/2016/10/A331518_1_En_10_Chapter_Equ9.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(9)</DIV></DIV>is a global binary solution of the adapted problem stated in Eq. (<SPAN class=InternalRef><A href=]() 4).
4).




 and following the steps in [6], the max-flow problem can be reformulated as the equivalent primal-dual model
and following the steps in [6], the max-flow problem can be reformulated as the equivalent primal-dual model
(7)
![$$\begin{aligned} \min _{u\in [0,1]}E(u)\mathbin {:=}\int \limits _{\Omega }\left\{ (1-u)C_{s}+uC_{t}+\alpha |{{\mathrm{\nabla _{{12}}}}}u|+\beta |u^{\prime }|\right\} {\mathrm{{d}}}{x}. \end{aligned}$$](/wp-content/uploads/2016/10/A331518_1_En_10_Chapter_Equ8.gif)
(8)
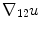 denotes the in-slice gradient and
denotes the in-slice gradient and 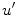 denotes the through-slice derivative of
denotes the through-slice derivative of  with respect to the
with respect to the  axis, similar to the definitions of
axis, similar to the definitions of  and
and  above. It can be shown that each level set function
above. It can be shown that each level set function ![$$u^{\ell }(x),\,\ell \in (0,1]$$](/wp-content/uploads/2016/10/A331518_1_En_10_Chapter_IEq41.gif) given by
given by
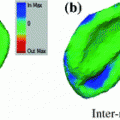
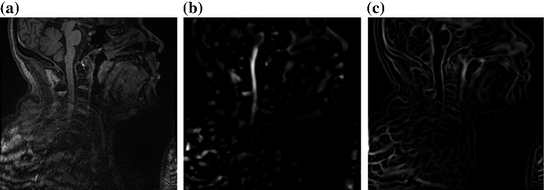
Fig. 2
Features used in segmentation. a Image intensities. b Vesselness response. c Csfness response
2.2 Tubularity Features
As our goal is to segment tubular structures in the image, it appears natural to include tubularity features in the flow capacity calculations. A well-known tubularity feature is Frangi’s measure of vesselness [9] (see Fig. 2b),  , where, for each scale
, where, for each scale 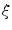 in the predefined set of scales
in the predefined set of scales 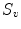 , the vesselness
, the vesselness  of bright tubular structures on dark background is
of bright tubular structures on dark background is

with  denoting the ordered eigenvalues (
denoting the ordered eigenvalues (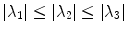 ) of the pointwise Hessian matrices that result from convolving the input image
) of the pointwise Hessian matrices that result from convolving the input image  with Gaussian derivatives of standard deviation
with Gaussian derivatives of standard deviation  . We define
. We define 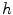 as half of the maximum Hessian norm at the current scale as suggested by Frangi [9].
as half of the maximum Hessian norm at the current scale as suggested by Frangi [9].
 , where, for each scale
, where, for each scale 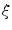 in the predefined set of scales
in the predefined set of scales 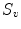 , the vesselness
, the vesselness  of bright tubular structures on dark background is
of bright tubular structures on dark background is
(10)
 denoting the ordered eigenvalues (
denoting the ordered eigenvalues (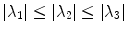 ) of the pointwise Hessian matrices that result from convolving the input image
) of the pointwise Hessian matrices that result from convolving the input image  with Gaussian derivatives of standard deviation
with Gaussian derivatives of standard deviation  . We define
. We define 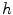 as half of the maximum Hessian norm at the current scale as suggested by Frangi [9].
as half of the maximum Hessian norm at the current scale as suggested by Frangi [9].In our experiments on segmenting the spinal cord, we decided to include another feature that specifically describes the background that immediately surrounds the target structure. The spinal cord is embedded in cerebrospinal fluid (CSF), which appears dark in the used MR sequences. As the CSF also appears largely elongated, but exhibits both tube-like and plate-like properties, we adapt Frangi’s vesselness feature to a csfness feature 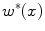 (see Fig. 2c) that discriminates between blob-like structures and non-blobs. We do so by replacing the eigenvalue ratio terms of
(see Fig. 2c) that discriminates between blob-like structures and non-blobs. We do so by replacing the eigenvalue ratio terms of 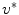 with an equivalent term composed of
with an equivalent term composed of 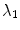 and
and 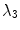 , as it is the latter ratio that discriminates both vessels and plates from blobs in Hessian eigenvalue analysis [9]. Consequently, we define
, as it is the latter ratio that discriminates both vessels and plates from blobs in Hessian eigenvalue analysis [9]. Consequently, we define  for dark non-blobs on bright background in the scales
for dark non-blobs on bright background in the scales  with
with

Combining the features. Let ![$$\mathcal {V}=[0,1]\ni v^{*}$$](/wp-content/uploads/2016/10/A331518_1_En_10_Chapter_IEq57.gif) ,
, ![$$\mathcal {W}=[0,1]\ni w^{*}$$](/wp-content/uploads/2016/10/A331518_1_En_10_Chapter_IEq58.gif) be the vesselness and csfness feature spaces, let
be the vesselness and csfness feature spaces, let  and
and 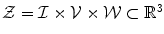 be two combined feature spaces, let
be two combined feature spaces, let  ,
,  be two new image functions that map to the combined feature spaces, and let
be two new image functions that map to the combined feature spaces, and let  ,
,  be the coordinates in the combined feature spaces.
be the coordinates in the combined feature spaces.
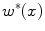 (see Fig. 2c) that discriminates between blob-like structures and non-blobs. We do so by replacing the eigenvalue ratio terms of
(see Fig. 2c) that discriminates between blob-like structures and non-blobs. We do so by replacing the eigenvalue ratio terms of 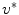 with an equivalent term composed of
with an equivalent term composed of 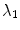 and
and 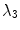 , as it is the latter ratio that discriminates both vessels and plates from blobs in Hessian eigenvalue analysis [9]. Consequently, we define
, as it is the latter ratio that discriminates both vessels and plates from blobs in Hessian eigenvalue analysis [9]. Consequently, we define  for dark non-blobs on bright background in the scales
for dark non-blobs on bright background in the scales  with
with
(11)
![$$\mathcal {V}=[0,1]\ni v^{*}$$](/wp-content/uploads/2016/10/A331518_1_En_10_Chapter_IEq57.gif) ,
, ![$$\mathcal {W}=[0,1]\ni w^{*}$$](/wp-content/uploads/2016/10/A331518_1_En_10_Chapter_IEq58.gif) be the vesselness and csfness feature spaces, let
be the vesselness and csfness feature spaces, let  and
and 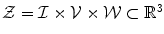 be two combined feature spaces, let
be two combined feature spaces, let  ,
,  be two new image functions that map to the combined feature spaces, and let
be two new image functions that map to the combined feature spaces, and let  ,
,  be the coordinates in the combined feature spaces.
be the coordinates in the combined feature spaces.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree