was achieved on the training data set.
1 Introduction
The spinal column forms an important support structure in the human body and mainly consists of the vertebral bones. As such, the vertebrae form an important part of the diagnosis, treatment planing and the understanding of various conditions affecting the spine. Thus, an accurate segmentation of the vertebrae is of relevance in several applications. The segmentation of the vertebrae is challenging, mainly due to shape variation and neighboring structures of similar intensity (e.g. other vertebrae, other bones and/or other tissues). To this end, the 2nd MICCAI workshop on Computational Methods and Clinical Applications for Spine Imaging has organized a segmentation challenge. This paper briefly describes one of the contributing methods and the achieved results.
2 Methods
The method used in this work for vertebra segmentation is inspired and to a large extent based upon the work presented in [2, 3], although some components have been changed and others have been added. This has been done to improve the performance but also since the work in [2, 3] was targeted at scoliotic spines. The most notable differences are the use of multiple gray-level atlases instead of a single binary model in the registration step, and the subsequent use of label fusion. The employed method consists of a preprocessing step, where an approximate position and rotation (pose) of each vertebra in the spines of both the target data set and the atlases are estimated. The preprocessing is followed by a registration step, where each atlas is registered to the target data set. The labels of the registered atlases are merged to a single label volume using label fusion to form the segmentation of the spine vertebrae in the target data set.
2.1 Preprocessing
The preprocessing consists of the following sub-steps:
1.
Spinal canal tracking—Seed points for the spinal canal are detected using the Hough transform on a thresholded axial image in the middle of the image volume. A growing and moving circle is used to detect the center of the spinal canal, and where the growing and moving circle process is repeated for each image as the spinal canal is tracked in both the cranial and the caudal direction.
2.
Disc detection—Given that the vertebrae are located anterior to the spinal canal, an intensity profile, running through the vertebrae, is sampled. The distinctive pattern of the intensity profile can be used to detect the position of the discs.
3.
Initial vertebral rotation estimation—In an image slice located between the detected discs, an initial axial vertebral rotation is estimated based upon minimizing an error measure for assessing the lateral symmetry between two halves of the image.
4.
Vertebra pose estimation—The two previous steps provide an initial estimate of the position and the orientation of each vertebra. To improve the pose estimate, an error measure is defined with six parameters ![$$ [x,y,z] $$](/wp-content/uploads/2016/10/A331518_1_En_18_Chapter_IEq2.gif) and
and ![$$ [\theta _X, \theta _Y, \theta _Z] $$](/wp-content/uploads/2016/10/A331518_1_En_18_Chapter_IEq3.gif) , defining the vertebra center-point and the vertebral orientation. The error measure is defined to assess the symmetry across various half-planes. The optimal parameters are found using Powell’s method.1 This step is similar to the method used in [5] for estimating the center-point and the orientation of the vertebrae in the spine.
, defining the vertebra center-point and the vertebral orientation. The error measure is defined to assess the symmetry across various half-planes. The optimal parameters are found using Powell’s method.1 This step is similar to the method used in [5] for estimating the center-point and the orientation of the vertebrae in the spine.
![$$ [x,y,z] $$](/wp-content/uploads/2016/10/A331518_1_En_18_Chapter_IEq2.gif) and
and ![$$ [\theta _X, \theta _Y, \theta _Z] $$](/wp-content/uploads/2016/10/A331518_1_En_18_Chapter_IEq3.gif) , defining the vertebra center-point and the vertebral orientation. The error measure is defined to assess the symmetry across various half-planes. The optimal parameters are found using Powell’s method.1 This step is similar to the method used in [5] for estimating the center-point and the orientation of the vertebrae in the spine.
, defining the vertebra center-point and the vertebral orientation. The error measure is defined to assess the symmetry across various half-planes. The optimal parameters are found using Powell’s method.1 This step is similar to the method used in [5] for estimating the center-point and the orientation of the vertebrae in the spine.The estimated pose is used for establishing an initial alignment between the vertebrae of the atlases and the vertebrae of the spine to segment.
2.2 Atlas-Based Registration
Given an initial alignment between the vertebrae of the target data set and an atlas, the vertebrae are then registered in groups of five, starting from the caudal end of the spine, i.e. L5-L1, L1-T9, T9-T5, T5-T1. A sub-volume is extracted from both the target data set and the atlas at hand, containing the vertebrae to be registered along with any surrounding vertebrae. After the initial alignment, a non-rigid registration step is applied, minimizing the local phase-difference [4]. For computational performance, an implementation of the non-rigid registration method on graphics processing units was used [1]. The finally computed transformation is used to deform the atlas onto the target data set, and, thus, the labels of the deformed atlas provide a segmentation of the vertebrae in the target data set.
2.3 Label Fusion
The final step is to merge the labels of the different deformed atlases into a single atlas volume. In this case, a straight forward majority voting has been employed for label fusion.
3 Data
The data used for evaluation consists of ten CT data sets acquired during daily clinical routine work in a trauma center, and is provided as training data for the 2nd MICCAI Workshop on Computational Methods and Clinical Applications for Spine Imaging. Information about the image data is found in [6]. Before processing, the image data was resampled to an isotropic resolution of 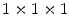 mm
mm using linear interpolation, in order to allow the usage of quadrature filters with isotropic resolution in the non-rigid registration step. Since ten data sets are available, each data set was segmented using the remaining nine as atlases.
using linear interpolation, in order to allow the usage of quadrature filters with isotropic resolution in the non-rigid registration step. Since ten data sets are available, each data set was segmented using the remaining nine as atlases.
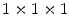 mm
mm using linear interpolation, in order to allow the usage of quadrature filters with isotropic resolution in the non-rigid registration step. Since ten data sets are available, each data set was segmented using the remaining nine as atlases.
using linear interpolation, in order to allow the usage of quadrature filters with isotropic resolution in the non-rigid registration step. Since ten data sets are available, each data set was segmented using the remaining nine as atlases.The ground truth data was compared with the segmentations obtained from the atlas-based segmentation using the DICE coefficient, defined as
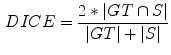
where 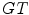 and
and 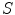 refer to the ground truth and the computed segmentations respectively, and where
refer to the ground truth and the computed segmentations respectively, and where 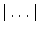 denotes the volume in voxels.
denotes the volume in voxels.
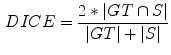
(1)
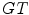 and
and 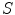 refer to the ground truth and the computed segmentations respectively, and where
refer to the ground truth and the computed segmentations respectively, and where 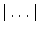 denotes the volume in voxels.
denotes the volume in voxels.4 Results
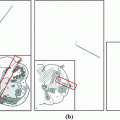
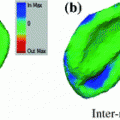
The results from the atlas-based segmentation of the ten CT data sets are provided in Table 1. In the results, it can be noted that lumbar vertebrae and the lower thoracic vertebrae, in general, obtain a DICE coefficient of 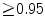 , which has to be considered as very good. Good scores are also achieved for the remaining thoracic vertebrae but where there are some vertebrae that appear to fail for data set #4 and #8. In addition, vertebra T1 obtains, almost consistently, lower scores than the other vertebrae. Example visualizations of the results are provided in Fig. 1. Note the failed segmentation of vertebrae T5-T8 in Fig. 1c, d, which correspond to the segmentation results for data set #8.
, which has to be considered as very good. Good scores are also achieved for the remaining thoracic vertebrae but where there are some vertebrae that appear to fail for data set #4 and #8. In addition, vertebra T1 obtains, almost consistently, lower scores than the other vertebrae. Example visualizations of the results are provided in Fig. 1. Note the failed segmentation of vertebrae T5-T8 in Fig. 1c, d, which correspond to the segmentation results for data set #8.
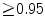 , which has to be considered as very good. Good scores are also achieved for the remaining thoracic vertebrae but where there are some vertebrae that appear to fail for data set #4 and #8. In addition, vertebra T1 obtains, almost consistently, lower scores than the other vertebrae. Example visualizations of the results are provided in Fig. 1. Note the failed segmentation of vertebrae T5-T8 in Fig. 1c, d, which correspond to the segmentation results for data set #8.
, which has to be considered as very good. Good scores are also achieved for the remaining thoracic vertebrae but where there are some vertebrae that appear to fail for data set #4 and #8. In addition, vertebra T1 obtains, almost consistently, lower scores than the other vertebrae. Example visualizations of the results are provided in Fig. 1. Note the failed segmentation of vertebrae T5-T8 in Fig. 1c, d, which correspond to the segmentation results for data set #8.Table 1
DICE scores as estimated from the atlas-based segmentation of the ten data sets
Vertebra/data set | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | All |
|---|---|---|---|---|---|---|---|---|---|---|---|
T1 | 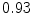 | 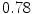 | 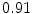 | 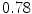 | 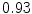 | 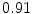 | 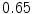 | 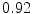 | 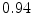 | 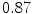 | 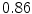 |
T2 | 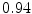 | 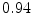 | 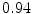 | 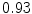 | 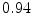 | 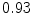 | 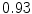 | 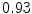 | 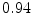 | 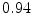 | 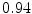 |
T3 | 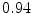 | 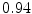 | 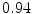 | 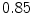 | 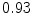 | 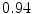 | 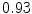 | 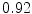 | 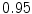 | 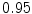 | 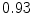 |
T4 | 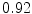 | 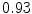 | 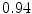 Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

|