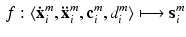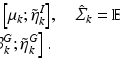Fig. 1.
Multi-scale CNN architecture used in our experiments. One stack of three pairs of convolution (Conv) and max-pooling layers (MP) uses input image patches of size 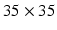 . The second stack comprises two pairs of convolution and max-pooling layers and uses input image patches of size
. The second stack comprises two pairs of convolution and max-pooling layers and uses input image patches of size 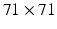 (centered at the same position). The resulting outputs
(centered at the same position). The resulting outputs 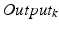 of the k pairs of convolution
of the k pairs of convolution 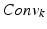 and max-pooling
and max-pooling 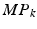 layers are the inputs for the succeeding layers, with corresponding convolution filter sizes
layers are the inputs for the succeeding layers, with corresponding convolution filter sizes 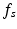 and sizes of the pooling regions
and sizes of the pooling regions 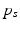 . Our CNN also comprises two fully connected layers (FC) and a terminal classification layer (CL). The outputs of both stacks are connected densely with all neurons of the first fully-connected layer. The location parameters are fed jointly with the activations of the second fully-connected layer into the classification layer.
. Our CNN also comprises two fully connected layers (FC) and a terminal classification layer (CL). The outputs of both stacks are connected densely with all neurons of the first fully-connected layer. The location parameters are fed jointly with the activations of the second fully-connected layer into the classification layer.
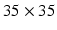 . The second stack comprises two pairs of convolution and max-pooling layers and uses input image patches of size
. The second stack comprises two pairs of convolution and max-pooling layers and uses input image patches of size 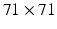 (centered at the same position). The resulting outputs
(centered at the same position). The resulting outputs 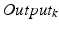 of the k pairs of convolution
of the k pairs of convolution 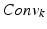 and max-pooling
and max-pooling 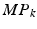 layers are the inputs for the succeeding layers, with corresponding convolution filter sizes
layers are the inputs for the succeeding layers, with corresponding convolution filter sizes 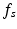 and sizes of the pooling regions
and sizes of the pooling regions 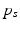 . Our CNN also comprises two fully connected layers (FC) and a terminal classification layer (CL). The outputs of both stacks are connected densely with all neurons of the first fully-connected layer. The location parameters are fed jointly with the activations of the second fully-connected layer into the classification layer.
. Our CNN also comprises two fully connected layers (FC) and a terminal classification layer (CL). The outputs of both stacks are connected densely with all neurons of the first fully-connected layer. The location parameters are fed jointly with the activations of the second fully-connected layer into the classification layer.2.1 Representing Inputs and Targets
The overall data comprises M tuples of medical imaging data, corresponding clinical reports and voxel-wise ground-truth class labels 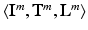 , with
, with 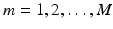 , where
, where 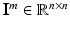 is an intensity image (e.g., a slice of an SD-OCT volume scan of the retina) of size
is an intensity image (e.g., a slice of an SD-OCT volume scan of the retina) of size 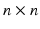 ,
, 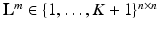 is an array of the same size containing the corresponding ground-truth class labels and
is an array of the same size containing the corresponding ground-truth class labels and 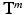 is the corresponding textual report. During training we are only given
is the corresponding textual report. During training we are only given 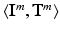 and train a classifier to predict
and train a classifier to predict 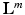 from
from 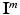 on new testing data. In this paper we propose a weakly supervised learning approach using semantic descriptions, where the voxel-level ground-truth class labels
on new testing data. In this paper we propose a weakly supervised learning approach using semantic descriptions, where the voxel-level ground-truth class labels 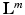 are not used for training but only for evaluation of the voxel-wise prediction accuracy.
are not used for training but only for evaluation of the voxel-wise prediction accuracy.
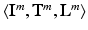 , with
, with 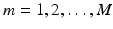 , where
, where 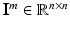 is an intensity image (e.g., a slice of an SD-OCT volume scan of the retina) of size
is an intensity image (e.g., a slice of an SD-OCT volume scan of the retina) of size 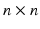 ,
, 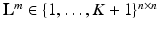 is an array of the same size containing the corresponding ground-truth class labels and
is an array of the same size containing the corresponding ground-truth class labels and 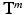 is the corresponding textual report. During training we are only given
is the corresponding textual report. During training we are only given 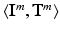 and train a classifier to predict
and train a classifier to predict 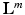 from
from 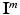 on new testing data. In this paper we propose a weakly supervised learning approach using semantic descriptions, where the voxel-level ground-truth class labels
on new testing data. In this paper we propose a weakly supervised learning approach using semantic descriptions, where the voxel-level ground-truth class labels 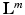 are not used for training but only for evaluation of the voxel-wise prediction accuracy.
are not used for training but only for evaluation of the voxel-wise prediction accuracy.Visual and Coordinate Input Information. To capture visual information at different levels of detail we extract small square-shaped image patches 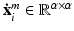 of size
of size 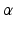 and larger square-shaped image patches
and larger square-shaped image patches 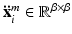 of size
of size 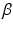 with
with 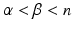 centered at the same spatial position
centered at the same spatial position 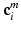 in volume
in volume 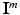 , where i is the index of the centroid of the image patch. For each image patch, we provide two additional quantitative location parameters to the network: (i) the 3D spatial coordinates
, where i is the index of the centroid of the image patch. For each image patch, we provide two additional quantitative location parameters to the network: (i) the 3D spatial coordinates 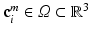 of the centroid i of the image patches and (ii) the Euclidean distance
of the centroid i of the image patches and (ii) the Euclidean distance 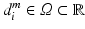 of the patch center i to a given reference structure (in our case: fovea) within the volume. We do not need to integrate these location parameters in the deep feature representation computation but inject them below the classification layer by concatenating the location parameters and activations of the fully-connected layer representing visual information (see Fig. 1). The same input information is provided for all experiments.
of the patch center i to a given reference structure (in our case: fovea) within the volume. We do not need to integrate these location parameters in the deep feature representation computation but inject them below the classification layer by concatenating the location parameters and activations of the fully-connected layer representing visual information (see Fig. 1). The same input information is provided for all experiments.
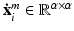 of size
of size 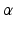 and larger square-shaped image patches
and larger square-shaped image patches 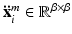 of size
of size 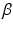 with
with 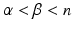 centered at the same spatial position
centered at the same spatial position 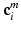 in volume
in volume 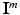 , where i is the index of the centroid of the image patch. For each image patch, we provide two additional quantitative location parameters to the network: (i) the 3D spatial coordinates
, where i is the index of the centroid of the image patch. For each image patch, we provide two additional quantitative location parameters to the network: (i) the 3D spatial coordinates 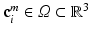 of the centroid i of the image patches and (ii) the Euclidean distance
of the centroid i of the image patches and (ii) the Euclidean distance 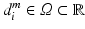 of the patch center i to a given reference structure (in our case: fovea) within the volume. We do not need to integrate these location parameters in the deep feature representation computation but inject them below the classification layer by concatenating the location parameters and activations of the fully-connected layer representing visual information (see Fig. 1). The same input information is provided for all experiments.
of the patch center i to a given reference structure (in our case: fovea) within the volume. We do not need to integrate these location parameters in the deep feature representation computation but inject them below the classification layer by concatenating the location parameters and activations of the fully-connected layer representing visual information (see Fig. 1). The same input information is provided for all experiments.Semantic Target Labels. We assume that objects (e.g. pathology) are reported together with a textual description of their approximate spatial location. Thus a report 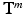 consists of K pairs of text snippets
consists of K pairs of text snippets 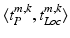 , with
, with 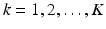 , where
, where 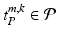 describes the occurrence of a specific object class term and
describes the occurrence of a specific object class term and 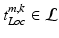 represents the semantic description of its spatial locations. These spatial locations can be both abstract subregions (e.g., centrally located) of the volume or concrete anatomical structures. Note that
represents the semantic description of its spatial locations. These spatial locations can be both abstract subregions (e.g., centrally located) of the volume or concrete anatomical structures. Note that 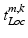 does not contain quantitative values, and we do not know the link between these descriptions and image coordinate information. This semantic information can come in
does not contain quantitative values, and we do not know the link between these descriptions and image coordinate information. This semantic information can come in 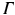 orthogonal semantic groups (e.g., in (1) the lowest layer and (2) close to the fovea). That is, different groups represent different location concepts found in clinical reports. The extraction of these pairs from the textual document is based on semantic parsing [15] and is not subject of this paper. We decompose the textual report
orthogonal semantic groups (e.g., in (1) the lowest layer and (2) close to the fovea). That is, different groups represent different location concepts found in clinical reports. The extraction of these pairs from the textual document is based on semantic parsing [15] and is not subject of this paper. We decompose the textual report 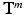 into the corresponding semantic target label
into the corresponding semantic target label 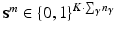 , with
, with 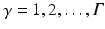 , where K is the number of different object classes which should be classified (e.g. cyst), and
, where K is the number of different object classes which should be classified (e.g. cyst), and 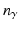 is the number of nominal region classes in one semantic group
is the number of nominal region classes in one semantic group 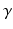 of descriptions (e.g.,
of descriptions (e.g., 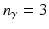 for upper vs. central vs. lower layer,
for upper vs. central vs. lower layer, 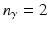 for close vs. far from reference structure). I.e., lets assume we have two groups, then
for close vs. far from reference structure). I.e., lets assume we have two groups, then 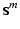 is a K-fold concatenation of pairs of a binary layer group
is a K-fold concatenation of pairs of a binary layer group 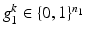 with
with 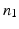 bits representing different layer classes and a binary reference location group
bits representing different layer classes and a binary reference location group 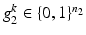 with
with 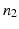 bits representing relative locations to a reference structure. For all object classes, all bits of the layer group, and all bits of the reference location group are set to 1, if they are mentioned mutually with the respective object class in the textual report. All bits of the corresponding layer group and all bits of the corresponding reference location group are set to 0, where the respective object class is not mentioned in the report. The vector
bits representing relative locations to a reference structure. For all object classes, all bits of the layer group, and all bits of the reference location group are set to 1, if they are mentioned mutually with the respective object class in the textual report. All bits of the corresponding layer group and all bits of the corresponding reference location group are set to 0, where the respective object class is not mentioned in the report. The vector 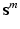 of semantic target labels is assigned to all input tuples
of semantic target labels is assigned to all input tuples 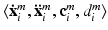 extracted from the corresponding volume
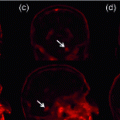
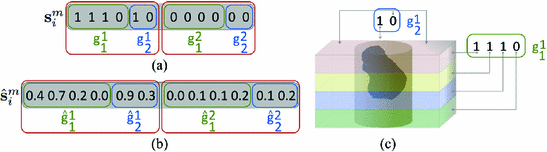
extracted from the corresponding volume  . Figure 2a shows an example of a semantic target label representation comprising two object classes. According to this binary representation the first object is mentioned mutually with layer classes 1, 2 and 3 and with reference location class 1 in the textual report. Figure 2c shows the corresponding volume information.
. Figure 2a shows an example of a semantic target label representation comprising two object classes. According to this binary representation the first object is mentioned mutually with layer classes 1, 2 and 3 and with reference location class 1 in the textual report. Figure 2c shows the corresponding volume information.
 consists of K pairs of text snippets
consists of K pairs of text snippets  , with
, with 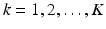 , where
, where 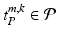 describes the occurrence of a specific object class term and
describes the occurrence of a specific object class term and 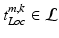 represents the semantic description of its spatial locations. These spatial locations can be both abstract subregions (e.g., centrally located) of the volume or concrete anatomical structures. Note that
represents the semantic description of its spatial locations. These spatial locations can be both abstract subregions (e.g., centrally located) of the volume or concrete anatomical structures. Note that 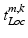 does not contain quantitative values, and we do not know the link between these descriptions and image coordinate information. This semantic information can come in
does not contain quantitative values, and we do not know the link between these descriptions and image coordinate information. This semantic information can come in 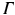 orthogonal semantic groups (e.g., in (1) the lowest layer and (2) close to the fovea). That is, different groups represent different location concepts found in clinical reports. The extraction of these pairs from the textual document is based on semantic parsing [15] and is not subject of this paper. We decompose the textual report
orthogonal semantic groups (e.g., in (1) the lowest layer and (2) close to the fovea). That is, different groups represent different location concepts found in clinical reports. The extraction of these pairs from the textual document is based on semantic parsing [15] and is not subject of this paper. We decompose the textual report 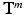 into the corresponding semantic target label
into the corresponding semantic target label 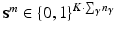 , with
, with 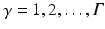 , where K is the number of different object classes which should be classified (e.g. cyst), and
, where K is the number of different object classes which should be classified (e.g. cyst), and 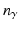 is the number of nominal region classes in one semantic group
is the number of nominal region classes in one semantic group 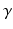 of descriptions (e.g.,
of descriptions (e.g., 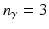 for upper vs. central vs. lower layer,
for upper vs. central vs. lower layer, 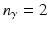 for close vs. far from reference structure). I.e., lets assume we have two groups, then
for close vs. far from reference structure). I.e., lets assume we have two groups, then 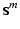 is a K-fold concatenation of pairs of a binary layer group
is a K-fold concatenation of pairs of a binary layer group 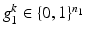 with
with 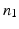 bits representing different layer classes and a binary reference location group
bits representing different layer classes and a binary reference location group 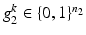 with
with 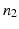 bits representing relative locations to a reference structure. For all object classes, all bits of the layer group, and all bits of the reference location group are set to 1, if they are mentioned mutually with the respective object class in the textual report. All bits of the corresponding layer group and all bits of the corresponding reference location group are set to 0, where the respective object class is not mentioned in the report. The vector
bits representing relative locations to a reference structure. For all object classes, all bits of the layer group, and all bits of the reference location group are set to 1, if they are mentioned mutually with the respective object class in the textual report. All bits of the corresponding layer group and all bits of the corresponding reference location group are set to 0, where the respective object class is not mentioned in the report. The vector 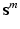 of semantic target labels is assigned to all input tuples
of semantic target labels is assigned to all input tuples 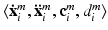 extracted from the corresponding volume
extracted from the corresponding volume 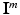 . Figure 2a shows an example of a semantic target label representation comprising two object classes. According to this binary representation the first object is mentioned mutually with layer classes 1, 2 and 3 and with reference location class 1 in the textual report. Figure 2c shows the corresponding volume information.
. Figure 2a shows an example of a semantic target label representation comprising two object classes. According to this binary representation the first object is mentioned mutually with layer classes 1, 2 and 3 and with reference location class 1 in the textual report. Figure 2c shows the corresponding volume information.
Fig. 2.
(a) Example of a semantic target label comprising two object classes (K = 2). Each of which comprises a layer group 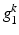 with 4 bits (layer 1,2,3, or 4) and a reference location group
with 4 bits (layer 1,2,3, or 4) and a reference location group 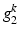 with 2 bits (close or distant). (b) Prediction of a semantic description
with 2 bits (close or distant). (b) Prediction of a semantic description 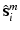 that would lead to a corresponding object class label prediction
that would lead to a corresponding object class label prediction 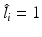 . (c) Visualization of the volume information which could lead to the given semantic target label shown in (a). (Best viewed in color) (Colour figure online)
. (c) Visualization of the volume information which could lead to the given semantic target label shown in (a). (Best viewed in color) (Colour figure online)
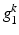 with 4 bits (layer 1,2,3, or 4) and a reference location group
with 4 bits (layer 1,2,3, or 4) and a reference location group 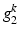 with 2 bits (close or distant). (b) Prediction of a semantic description
with 2 bits (close or distant). (b) Prediction of a semantic description 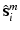 that would lead to a corresponding object class label prediction
that would lead to a corresponding object class label prediction 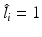 . (c) Visualization of the volume information which could lead to the given semantic target label shown in (a). (Best viewed in color) (Colour figure online)
. (c) Visualization of the volume information which could lead to the given semantic target label shown in (a). (Best viewed in color) (Colour figure online)Voxel-wise Ground Truth Labels. To evaluate the algorithm, we use the ground-truth class label 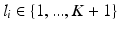 from
from 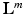 at the center position
at the center position 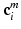 of the patches for every multi-scale image patch pair
of the patches for every multi-scale image patch pair 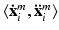 . Labels include the reported observations
. Labels include the reported observations 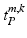 and a healthy background label.
and a healthy background label. 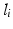 is assigned to the whole multi-scale image patch pair
is assigned to the whole multi-scale image patch pair 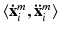 centered at voxel position i.
centered at voxel position i.
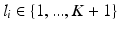 from
from 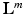 at the center position
at the center position 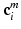 of the patches for every multi-scale image patch pair
of the patches for every multi-scale image patch pair 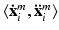 . Labels include the reported observations
. Labels include the reported observations 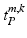 and a healthy background label.
and a healthy background label. 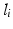 is assigned to the whole multi-scale image patch pair
is assigned to the whole multi-scale image patch pair 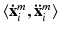 centered at voxel position i.
centered at voxel position i.2.2 Training to Predict Semantic Descriptors
We train a CNN to predict the semantic description from the imaging data and the corresponding location information provided for the patch center voxels. We use tuples 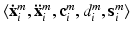 for weakly supervised training of our model. The training objective is to learn the mapping
for weakly supervised training of our model. The training objective is to learn the mapping
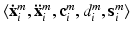 for weakly supervised training of our model. The training objective is to learn the mapping
for weakly supervised training of our model. The training objective is to learn the mapping