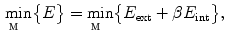contain three-dimensional (3D) images of the thoracolumbar spine, where each image is assigned a series of binary masks representing reference segmentations of each individual thoracolumbar vertebra from level T1 to L5, and let each vertebral level be represented by a 3D face-vertex mesh 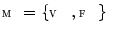 of
of 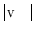 vertices and
vertices and 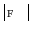 faces (i.e. triangles). A chain of mean vertebra shape models represents the mean shape model of the whole thoracolumbar spine used for spine detection, while the mean shape models of individual vertebrae are used for vertebra detection and segmentation in an unknown 3D image
faces (i.e. triangles). A chain of mean vertebra shape models represents the mean shape model of the whole thoracolumbar spine used for spine detection, while the mean shape models of individual vertebrae are used for vertebra detection and segmentation in an unknown 3D image 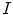 .
.
1.1 Vertebra Detection
The detection of vertebrae in an unknown 3D image 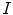 was performed by a novel optimization scheme based on interpolation theory [3], which consists of three steps: spine detection, vertebra detection and vertebra alignment. To detect the spine in image
was performed by a novel optimization scheme based on interpolation theory [3], which consists of three steps: spine detection, vertebra detection and vertebra alignment. To detect the spine in image 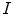 , the pose of the mean shape model of the thoracolumbar spine
, the pose of the mean shape model of the thoracolumbar spine 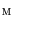 is optimized against three translations (i.e. coordinates
is optimized against three translations (i.e. coordinates 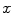 ,
, 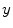 and
and 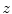 representing sagittal, coronal and axial anatomical directions, respectively), and the resulting global maximum represents the location of the spine in the 3D image, which is further used to initialize the vertebra detection. To detect each vertebra, the pose of the corresponding mean vertebra shape model
representing sagittal, coronal and axial anatomical directions, respectively), and the resulting global maximum represents the location of the spine in the 3D image, which is further used to initialize the vertebra detection. To detect each vertebra, the pose of the corresponding mean vertebra shape model 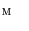 is optimized against three translations, however, in this case all local maxima of the resulting interpolation are extracted, corresponding to locations of the observed and neighboring vertebrae. The correct location of each vertebra is determined by the optimal path that passes through a set of locations, where each location corresponds to a local maximum at a different vertebral level. Finally, a more accurate alignment of the mean vertebra shape model is performed by optimizing the pose of each model against three translations, one scaling (i.e. factor
is optimized against three translations, however, in this case all local maxima of the resulting interpolation are extracted, corresponding to locations of the observed and neighboring vertebrae. The correct location of each vertebra is determined by the optimal path that passes through a set of locations, where each location corresponds to a local maximum at a different vertebral level. Finally, a more accurate alignment of the mean vertebra shape model is performed by optimizing the pose of each model against three translations, one scaling (i.e. factor 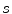 ) and three rotations (i.e. angles
) and three rotations (i.e. angles 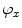 ,
, 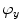 and
and 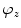 about coordinate axes
about coordinate axes 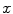 ,
, 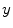 and
and 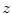 , respectively). The resulting alignment represents the final vertebra detection result.
, respectively). The resulting alignment represents the final vertebra detection result.
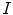 was performed by a novel optimization scheme based on interpolation theory [3], which consists of three steps: spine detection, vertebra detection and vertebra alignment. To detect the spine in image
was performed by a novel optimization scheme based on interpolation theory [3], which consists of three steps: spine detection, vertebra detection and vertebra alignment. To detect the spine in image 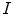 , the pose of the mean shape model of the thoracolumbar spine
, the pose of the mean shape model of the thoracolumbar spine 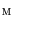 is optimized against three translations (i.e. coordinates
is optimized against three translations (i.e. coordinates 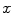 ,
, 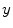 and
and 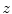 representing sagittal, coronal and axial anatomical directions, respectively), and the resulting global maximum represents the location of the spine in the 3D image, which is further used to initialize the vertebra detection. To detect each vertebra, the pose of the corresponding mean vertebra shape model
representing sagittal, coronal and axial anatomical directions, respectively), and the resulting global maximum represents the location of the spine in the 3D image, which is further used to initialize the vertebra detection. To detect each vertebra, the pose of the corresponding mean vertebra shape model 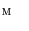 is optimized against three translations, however, in this case all local maxima of the resulting interpolation are extracted, corresponding to locations of the observed and neighboring vertebrae. The correct location of each vertebra is determined by the optimal path that passes through a set of locations, where each location corresponds to a local maximum at a different vertebral level. Finally, a more accurate alignment of the mean vertebra shape model is performed by optimizing the pose of each model against three translations, one scaling (i.e. factor
is optimized against three translations, however, in this case all local maxima of the resulting interpolation are extracted, corresponding to locations of the observed and neighboring vertebrae. The correct location of each vertebra is determined by the optimal path that passes through a set of locations, where each location corresponds to a local maximum at a different vertebral level. Finally, a more accurate alignment of the mean vertebra shape model is performed by optimizing the pose of each model against three translations, one scaling (i.e. factor 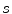 ) and three rotations (i.e. angles
) and three rotations (i.e. angles 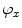 ,
, 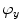 and
and 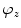 about coordinate axes
about coordinate axes 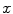 ,
, 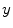 and
and 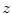 , respectively). The resulting alignment represents the final vertebra detection result.
, respectively). The resulting alignment represents the final vertebra detection result.1.2 Vertebra Segmentation
After the interpolation-based alignment [3], segmentation of each vertebra in the unknown image 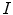 is performed by an improved mesh deformation technique [5] that moves mesh vertices to their optimal locations while preserving the underlying vertebral shape [4, 6]. In this iterative procedure, the image object detection for mesh face centroids that are represented by the centers of mass for mesh faces
is performed by an improved mesh deformation technique [5] that moves mesh vertices to their optimal locations while preserving the underlying vertebral shape [4, 6]. In this iterative procedure, the image object detection for mesh face centroids that are represented by the centers of mass for mesh faces 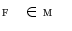 and reconfiguration of mesh vertices
and reconfiguration of mesh vertices 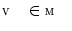 are executed in each iteration.
are executed in each iteration.
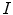 is performed by an improved mesh deformation technique [5] that moves mesh vertices to their optimal locations while preserving the underlying vertebral shape [4, 6]. In this iterative procedure, the image object detection for mesh face centroids that are represented by the centers of mass for mesh faces
is performed by an improved mesh deformation technique [5] that moves mesh vertices to their optimal locations while preserving the underlying vertebral shape [4, 6]. In this iterative procedure, the image object detection for mesh face centroids that are represented by the centers of mass for mesh faces 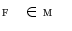 and reconfiguration of mesh vertices
and reconfiguration of mesh vertices 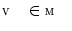 are executed in each iteration.
are executed in each iteration.1.2.1 Object Detection
By displacing each mesh face centroid 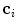 ;
; 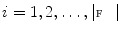 along its corresponding mesh face normal
along its corresponding mesh face normal 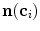 , a new candidate mesh face centroid
, a new candidate mesh face centroid 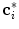 is found in each
is found in each 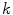 -th iteration:
-th iteration:
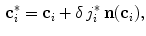
where 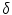 is the length of the unit displacement, and
is the length of the unit displacement, and 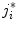 is an element from set
is an element from set 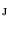 ;
; 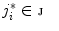 . Set
. Set 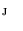 represents the search profile along
represents the search profile along 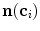 , called the sampling parcel:
, called the sampling parcel:
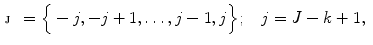
which is of size 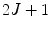 at initial iteration
at initial iteration 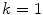 and
and 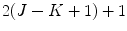 at final iteration
at final iteration 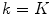 . The element
. The element 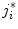 that defines the location of
that defines the location of 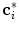 is determined by detecting vertebra boundaries:
is determined by detecting vertebra boundaries:
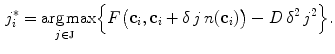
where 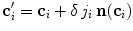 is the candidate location for
is the candidate location for 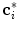 (Eq. 1), and parameter
(Eq. 1), and parameter 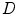 controls the tradeoff between the distance from
controls the tradeoff between the distance from 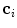 to
to 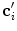 and the response of the boundary detection operator
and the response of the boundary detection operator 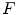 :
:
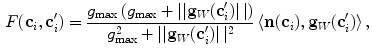
where 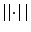 denotes the vector norm,
denotes the vector norm, 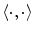 denotes the dot product,
denotes the dot product,  is the estimated mean amplitude of intensity gradients at vertebra boundaries that is used to suppresses the weighted gradients, which may occur if the gradient magnitude at the boundary of the object of interest is considerably smaller than of another object in its neighborhood (e.g. pedicle screws), and
is the estimated mean amplitude of intensity gradients at vertebra boundaries that is used to suppresses the weighted gradients, which may occur if the gradient magnitude at the boundary of the object of interest is considerably smaller than of another object in its neighborhood (e.g. pedicle screws), and  is the image apperance operator at candidate mesh centroid location
is the image apperance operator at candidate mesh centroid location 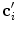 :
:
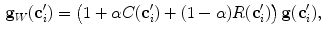
where ![$$C(\mathbf {c}_i')\in [0, 1]$$](/wp-content/uploads/2016/10/A331518_1_En_21_Chapter_IEq51.gif) is the response to the Canny edge operator,
is the response to the Canny edge operator, ![$$R(\mathbf {c}_i')\in [-1,1]$$](/wp-content/uploads/2016/10/A331518_1_En_21_Chapter_IEq52.gif) is a random forest [1] regression model build upon an intensity-based descriptor and
is a random forest [1] regression model build upon an intensity-based descriptor and 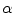 is the weighting parameter.
is the weighting parameter.
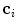 ;
; 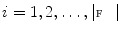 along its corresponding mesh face normal
along its corresponding mesh face normal 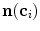 , a new candidate mesh face centroid
, a new candidate mesh face centroid 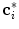 is found in each
is found in each 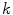 -th iteration:
-th iteration: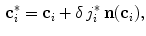
(1)
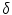 is the length of the unit displacement, and
is the length of the unit displacement, and 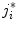 is an element from set
is an element from set 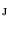 ;
; 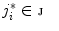 . Set
. Set 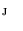 represents the search profile along
represents the search profile along 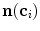 , called the sampling parcel:
, called the sampling parcel: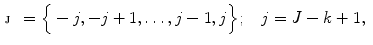
(2)
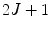 at initial iteration
at initial iteration 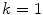 and
and 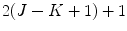 at final iteration
at final iteration 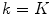 . The element
. The element 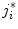 that defines the location of
that defines the location of 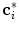 is determined by detecting vertebra boundaries:
is determined by detecting vertebra boundaries: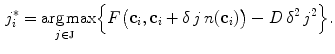
(3)
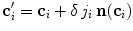 is the candidate location for
is the candidate location for 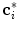 (Eq. 1), and parameter
(Eq. 1), and parameter 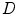 controls the tradeoff between the distance from
controls the tradeoff between the distance from 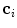 to
to 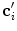 and the response of the boundary detection operator
and the response of the boundary detection operator 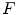 :
: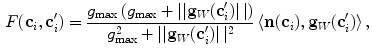
(4)
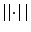 denotes the vector norm,
denotes the vector norm, 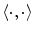 denotes the dot product,
denotes the dot product, 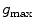 is the estimated mean amplitude of intensity gradients at vertebra boundaries that is used to suppresses the weighted gradients, which may occur if the gradient magnitude at the boundary of the object of interest is considerably smaller than of another object in its neighborhood (e.g. pedicle screws), and
is the estimated mean amplitude of intensity gradients at vertebra boundaries that is used to suppresses the weighted gradients, which may occur if the gradient magnitude at the boundary of the object of interest is considerably smaller than of another object in its neighborhood (e.g. pedicle screws), and 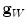 is the image apperance operator at candidate mesh centroid location
is the image apperance operator at candidate mesh centroid location 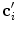 :
: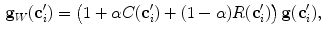
(5)
![$$C(\mathbf {c}_i')\in [0, 1]$$](/wp-content/uploads/2016/10/A331518_1_En_21_Chapter_IEq51.gif) is the response to the Canny edge operator,
is the response to the Canny edge operator, ![$$R(\mathbf {c}_i')\in [-1,1]$$](/wp-content/uploads/2016/10/A331518_1_En_21_Chapter_IEq52.gif) is a random forest [1] regression model build upon an intensity-based descriptor and
is a random forest [1] regression model build upon an intensity-based descriptor and 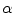 is the weighting parameter.
is the weighting parameter.1.2.2 Mesh Reconfiguration
Once the new candidate mesh face centroids 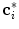 are detected, mesh
are detected, mesh 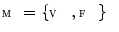 is reconfigured in each
is reconfigured in each 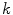 -th iteration by minimizing the weighted sum
-th iteration by minimizing the weighted sum 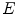 of energy terms:
of energy terms:
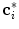 are detected, mesh
are detected, mesh 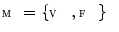 is reconfigured in each
is reconfigured in each 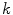 -th iteration by minimizing the weighted sum
-th iteration by minimizing the weighted sum 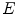 of energy terms:
of energy terms: