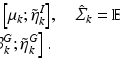Fig. 1.
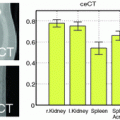
3D SD-OCT reconstruction of a (a) healthy retina with the foveal pit in the center, and (b) a retina with edema, where the swelling of the retina is caused by cystic and subretinal fluid (c).
Contribution. In this paper we propose a method to predict treatment outcome based on observations made during early stages of treatment. We identify interpretable biomarkers in longitudinal imaging data for prediction. To compare features through follow-up examinations, and across patients, we obtain a joint coordinate reference space from retinal OCT images by intra-patient and inter-patient registration using fundus and OCT image landmarks. From pixel-wise features extracted from the initial three months within the reference frame coordinate system we predict the treatment response of recurrence vs. non-recurrence of macular edema in a 12 month follow-up using elastic net regularized generalized linear models. Furthermore, we predict the time-point of the first recurrence of edema. Cross-validation experiments demonstrate that the proposed method yields good prediction accuracy and interpretable results. Furthermore, we show that longitudinal features together with time-to-event survival statistics in the Cox proportional hazard model increase time-to-recurrence prediction accuracy.
Related Work. We pose the prediction of treatment response as a multi-variate regression problem. In the following, we briefly review relevant related approaches. By treating each pixel/voxel or small groups of pixels as a single feature we are operating in a high-dimension-low-sample-size setting, where the feature dimension size p is several orders of magnitude larger than the number of patients n (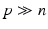 ). Multivariate sparse linear regression methods, for instance Lasso [3] or elastic net [4] as well as non-linear regression methods such as Random Forests [5] are able to provide a prediction in such a setting [6, 7]. In addition, they compute measures of feature-importance enabling insight into disease mechanisms. Such feature selection methods are used for instance in gene expression studies [8], fMRI network analysis [9] or predictions in structural neuroimages [10]. Most of these studies focus on prediction of the present condition from images, not dealing with the prediction of the future.
). Multivariate sparse linear regression methods, for instance Lasso [3] or elastic net [4] as well as non-linear regression methods such as Random Forests [5] are able to provide a prediction in such a setting [6, 7]. In addition, they compute measures of feature-importance enabling insight into disease mechanisms. Such feature selection methods are used for instance in gene expression studies [8], fMRI network analysis [9] or predictions in structural neuroimages [10]. Most of these studies focus on prediction of the present condition from images, not dealing with the prediction of the future.
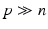 ). Multivariate sparse linear regression methods, for instance Lasso [3] or elastic net [4] as well as non-linear regression methods such as Random Forests [5] are able to provide a prediction in such a setting [6, 7]. In addition, they compute measures of feature-importance enabling insight into disease mechanisms. Such feature selection methods are used for instance in gene expression studies [8], fMRI network analysis [9] or predictions in structural neuroimages [10]. Most of these studies focus on prediction of the present condition from images, not dealing with the prediction of the future.
). Multivariate sparse linear regression methods, for instance Lasso [3] or elastic net [4] as well as non-linear regression methods such as Random Forests [5] are able to provide a prediction in such a setting [6, 7]. In addition, they compute measures of feature-importance enabling insight into disease mechanisms. Such feature selection methods are used for instance in gene expression studies [8], fMRI network analysis [9] or predictions in structural neuroimages [10]. Most of these studies focus on prediction of the present condition from images, not dealing with the prediction of the future.Sabuncu [11] proposed a sparse Bayesian multivariate prediction model combined with a survival model for studying longitudinal follow-up data. He demonstrated that an image based time-to-event prediction improves the result compared to a binary classification of converter/non-converter. Bogunović et al. [12] proposed a machine learning approach to predict the treatment response from retinal OCT in patients with age-related macular degeneration by classifying quantitative features extracted from the fovea center aligned image data.
To compensate for the anatomical variation in imaging studies the individual data is usually mapped to a common coordinate system or atlas [13]. Spatial variations in retinal images arise from different scanning positions and the varying anatomy of the retina across subjects. To ensure spatial consistency across the retinal data Abràmoff et al. [14] described a method to normalize eye fundus images by using visible landmarks such as the optic disc center, the fovea, and the main vessel arcades. Due to the smaller field of view of clinical OCT images compared to fundus images not all of these landmarks are available in OCT.
2 Spatio-Temporal Features in a Joint Reference Space
We normalize the retinal OCT images by transforming the data into a joint reference coordinate system using intra-patient follow-up registration based on the vessel structure, and inter-patient alignment via landmarks visible in OCT and fundus images.
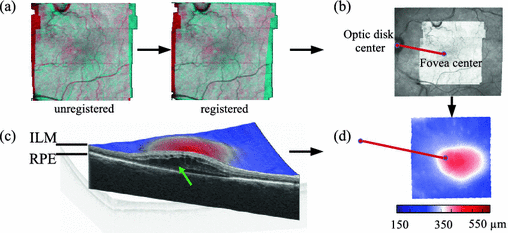

Fig. 2.
Steps to get spatio-temporal signatures in a joint reference space: (a) Intra-patient registration via vessel structure. For illustration purpose 2D projections from OCTs of two time-points are overlayed and colored blue resp. red. The steps in the projections come from the motion-correction. (b) Inter-patient alignment via fovea center and optic disk center. (c) Disease features as total retinal thickness maps are obtained by measuring the distance between the ILM layer and RPE layer. The cut through the retina reveals the pathological cystic structure causing edema (green arrow). (d) Transformation of the thickness maps into the reference frame (Color figure online).
First, we reduce motion artefacts introduced by patient movement during acquisition by the method described in [15]. To obtain landmarks for the intra-patient follow-up registration, automatic vessel segmentation is performed on the OCT images. Parameters for the affine registration are generated by applying Coherent Point Drift [16] to the segmented retinal vessel point sets, as described in [17] (Fig. 2a). The inter-patient affine registration is performed by aligning the fovea center and the optic disk center within patients (Fig. 2b). Due to the limited field of view of the macular centered OCT the optic disk is only visible in the corresponding fundus image. Hence, a registration of the fundus image to OCT is performed using the projection of the OCT image, registered rigidly to the fundus image by minimizing the normalized cross-correlation of the intensity values. The foveal center landmark (center of the foveal pit) (Fig. 1a), was set manually by expert readers. The optic disk center was identified by applying circular Hough transformation with varying radii on the binary threshold fundus image, and picking the circle showing the highest response. The optic disk center position is the center of the circle. Since the quality of the fundus images obtained by the OCT-scanner varies substantially, and the fovea center is sometimes hard to identify in cases with heavy pathology, we chose as reference scan the time-point at which the foveal center as well as the optic disc center could be accurately determined. All other scans in the time-series were transformed to the selected one, and the reference scan was aligned with the other patients. Scans from the right eye were mirrored, in order to align their anatomy with scans from the left eye.
Spatio-temporal Signature of Disease. Total retinal thickness maps 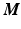 are computed as the distance between the inner limiting membrane (ILM) surface, which is the boundary between the retina and the vitreous body, and the retinal pigment epithelium (RPE), which is the border between the retina and the choroid (Fig. 2c). These layers are identified using a graph-based surface segmentation algorithm [18]. These maps are transformed into the reference space using the obtained affine transformation (Fig. 2d).
are computed as the distance between the inner limiting membrane (ILM) surface, which is the boundary between the retina and the vitreous body, and the retinal pigment epithelium (RPE), which is the border between the retina and the choroid (Fig. 2c). These layers are identified using a graph-based surface segmentation algorithm [18]. These maps are transformed into the reference space using the obtained affine transformation (Fig. 2d).
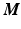 are computed as the distance between the inner limiting membrane (ILM) surface, which is the boundary between the retina and the vitreous body, and the retinal pigment epithelium (RPE), which is the border between the retina and the choroid (Fig. 2c). These layers are identified using a graph-based surface segmentation algorithm [18]. These maps are transformed into the reference space using the obtained affine transformation (Fig. 2d).
are computed as the distance between the inner limiting membrane (ILM) surface, which is the boundary between the retina and the vitreous body, and the retinal pigment epithelium (RPE), which is the border between the retina and the choroid (Fig. 2c). These layers are identified using a graph-based surface segmentation algorithm [18]. These maps are transformed into the reference space using the obtained affine transformation (Fig. 2d).Let 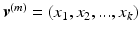 be the vectorized pixel values from the transformed thickness map
be the vectorized pixel values from the transformed thickness map 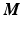 for the month m. By concatenating the thickness map vectors and the change of thickness over time up to month m, a spatio-temporal signature vector is obtained for each individual:
for the month m. By concatenating the thickness map vectors and the change of thickness over time up to month m, a spatio-temporal signature vector is obtained for each individual: 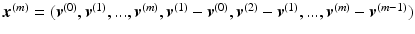 . These signatures are pooled in a matrix
. These signatures are pooled in a matrix 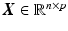 , where each row represents a signature vector of a subject and each column is a distinct spatio-temporal anatomical position in the retina.
, where each row represents a signature vector of a subject and each column is a distinct spatio-temporal anatomical position in the retina. 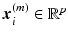 is the signature vector for subject i.
is the signature vector for subject i.
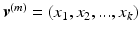 be the vectorized pixel values from the transformed thickness map
be the vectorized pixel values from the transformed thickness map 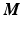 for the month m. By concatenating the thickness map vectors and the change of thickness over time up to month m, a spatio-temporal signature vector is obtained for each individual:
for the month m. By concatenating the thickness map vectors and the change of thickness over time up to month m, a spatio-temporal signature vector is obtained for each individual: 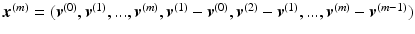 . These signatures are pooled in a matrix
. These signatures are pooled in a matrix 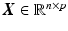 , where each row represents a signature vector of a subject and each column is a distinct spatio-temporal anatomical position in the retina.
, where each row represents a signature vector of a subject and each column is a distinct spatio-temporal anatomical position in the retina. 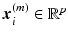 is the signature vector for subject i.
is the signature vector for subject i.3 Prediction of Recurrence
We predict the treatment response based on data up to the initial loading phase of three monthly injections. Specifically, we predict for an individual based on the corresponding spatio-temporal signature 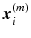 covering the three month loading phase, if a treated edema will recur in the future. In a second task we predict at which time-point the first recurrence happens for patients with recurring edema. For notational clarity, we drop the time-index
covering the three month loading phase, if a treated edema will recur in the future. In a second task we predict at which time-point the first recurrence happens for patients with recurring edema. For notational clarity, we drop the time-index 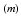 in the following explanation.
in the following explanation.
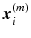 covering the three month loading phase, if a treated edema will recur in the future. In a second task we predict at which time-point the first recurrence happens for patients with recurring edema. For notational clarity, we drop the time-index
covering the three month loading phase, if a treated edema will recur in the future. In a second task we predict at which time-point the first recurrence happens for patients with recurring edema. For notational clarity, we drop the time-index 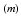 in the following explanation.
in the following explanation.3.1 Prediction by Sparse Linear Regression
We assume that the continuous response variable 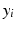 for an individual i is a weighted linear combination of the input variables
for an individual i is a weighted linear combination of the input variables 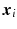 :
: 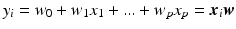 . The coefficients (or weights)
. The coefficients (or weights) 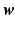 are estimated for a training-set
are estimated for a training-set 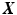 in a regularized way by minimizing the following objective function:
in a regularized way by minimizing the following objective function:
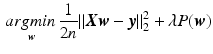
Since in our case the system is strongly underdetermined (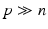 ), a regularization function P is necessary, where
), a regularization function P is necessary, where 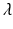 controls the amount of regularization. Recently, sparsity has been proposed as property of the coefficients [3, 8], where only a few but relevant coefficients
controls the amount of regularization. Recently, sparsity has been proposed as property of the coefficients [3, 8], where only a few but relevant coefficients 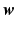 are non-zero, highlighting predictive anatomical regions and time-points. Sparsity can be obtained by applying the
are non-zero, highlighting predictive anatomical regions and time-points. Sparsity can be obtained by applying the 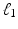 norm on
norm on 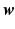 , known as Lasso regularization [3]. When features are strongly correlated, Lasso tends to pick only one of these features at random. Thus, Zou and Hastie proposed elastic net regularization [4] to overcome the limitation of Lasso regularization, by combining the
, known as Lasso regularization [3]. When features are strongly correlated, Lasso tends to pick only one of these features at random. Thus, Zou and Hastie proposed elastic net regularization [4] to overcome the limitation of Lasso regularization, by combining the 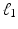 norm with a ridge regularization (
norm with a ridge regularization (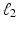 norm):
norm):
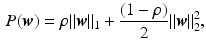
where 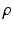 defines the ratio of the convex combination of
defines the ratio of the convex combination of 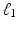 and
and 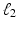 regularization.
regularization.
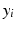 for an individual i is a weighted linear combination of the input variables
for an individual i is a weighted linear combination of the input variables 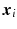 :
: 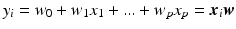 . The coefficients (or weights)
. The coefficients (or weights) 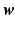 are estimated for a training-set
are estimated for a training-set 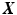 in a regularized way by minimizing the following objective function:
in a regularized way by minimizing the following objective function: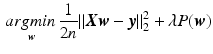
(1)
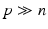 ), a regularization function P is necessary, where
), a regularization function P is necessary, where 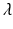 controls the amount of regularization. Recently, sparsity has been proposed as property of the coefficients [3, 8], where only a few but relevant coefficients
controls the amount of regularization. Recently, sparsity has been proposed as property of the coefficients [3, 8], where only a few but relevant coefficients 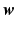 are non-zero, highlighting predictive anatomical regions and time-points. Sparsity can be obtained by applying the
are non-zero, highlighting predictive anatomical regions and time-points. Sparsity can be obtained by applying the 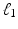 norm on
norm on 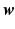 , known as Lasso regularization [3]. When features are strongly correlated, Lasso tends to pick only one of these features at random. Thus, Zou and Hastie proposed elastic net regularization [4] to overcome the limitation of Lasso regularization, by combining the
, known as Lasso regularization [3]. When features are strongly correlated, Lasso tends to pick only one of these features at random. Thus, Zou and Hastie proposed elastic net regularization [4] to overcome the limitation of Lasso regularization, by combining the 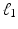 norm with a ridge regularization (
norm with a ridge regularization (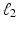 norm):
norm):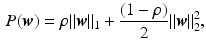
(2)
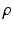 defines the ratio of the convex combination of
defines the ratio of the convex combination of 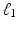 and
and 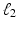 regularization.
regularization.The features 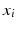 with non-zero coefficients
with non-zero coefficients 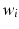 represent anatomical locations and time-points whose characteristics are informative for the prediction. They enable interpretation by ophthalmologists.
represent anatomical locations and time-points whose characteristics are informative for the prediction. They enable interpretation by ophthalmologists.
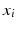 with non-zero coefficients
with non-zero coefficients 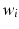 represent anatomical locations and time-points whose characteristics are informative for the prediction. They enable interpretation by ophthalmologists.
represent anatomical locations and time-points whose characteristics are informative for the prediction. They enable interpretation by ophthalmologists.3.2 Categorical Variable Prediction
Using a generalized version of the sparse linear regression, where the outcome variable y is replaced by a function, categorical variables can be predicted using logistic regression. The probabilities of the binary outcomes are modeled as logit function (log of the odds): 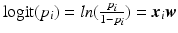 , where
, where 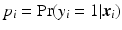 . To obtain the coefficients Eq. 1 is modified such that:
. To obtain the coefficients Eq. 1 is modified such that:
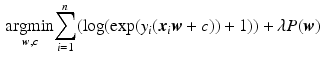
The class probability 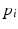 for a new case with covariates
for a new case with covariates 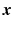 can be predicted from the trained weights via the inverse logit:
can be predicted from the trained weights via the inverse logit: 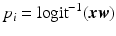 .
.
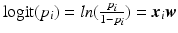 , where
, where 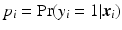 . To obtain the coefficients Eq. 1 is modified such that:
. To obtain the coefficients Eq. 1 is modified such that: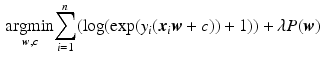
(3)
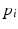 for a new case with covariates
for a new case with covariates 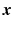 can be predicted from the trained weights via the inverse logit:
can be predicted from the trained weights via the inverse logit: 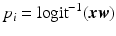 .
.We compute the coefficients 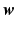 by training an elastic net regularized logistic regression model using the spatio-temporal signature matrix
by training an elastic net regularized logistic regression model using the spatio-temporal signature matrix 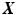 and the binary outcome labels
and the binary outcome labels 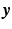 of non-recurring/recurring edema within 12 months. By applying the trained model on an unseen case we obtain the probability of recurrence
of non-recurring/recurring edema within 12 months. By applying the trained model on an unseen case we obtain the probability of recurrence 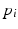 . Finally, we threshold the probability in order to obtain a binary outcome.
. Finally, we threshold the probability in order to obtain a binary outcome.
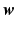 by training an elastic net regularized logistic regression model using the spatio-temporal signature matrix
by training an elastic net regularized logistic regression model using the spatio-temporal signature matrix 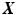 and the binary outcome labels
and the binary outcome labels 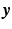 of non-recurring/recurring edema within 12 months. By applying the trained model on an unseen case we obtain the probability of recurrence
of non-recurring/recurring edema within 12 months. By applying the trained model on an unseen case we obtain the probability of recurrence 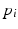 . Finally, we threshold the probability in order to obtain a binary outcome.
. Finally, we threshold the probability in order to obtain a binary outcome.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree