Simplistic Theory of the Functions of the Ensemble of the Electrons, Atoms, Molecules, Nuclei, in the Brain

and Rakhi Kaila²

(1)

School of Physics, University of New South Wales, Sydney, NSW, Australia

(2)

School of Medicine, University of New South Wales, Sydney, NSW, Australia

Abstract

One should realize that the quantum science is not as much a common knowledge as the Newtonian Science is. It thus becomes a formidable task, to propagate further about the new developments in the brain science. The neuroscience audience who this work should attract the most would normally have little and basically no exposure to the basics of the quantum physic so deeply rooted in the dynamics of the atoms, molecules, tissues, etc., in the brain. However an effort at grass roots level is made in this work in that direction. To keep it simple explanation is made by reference to diagrams drawn. It is a rough spin model picture of the brain MRI that is exposed here. It is as if it were a collection of ordered spins in an ensemble of molecules in the direction of the static magnetic field naturally present around the nucleus. Spins in molecules are surrounded by smeared out orbital electron cloud of the molecules, fluids, tissue, etc. There are as many electrons in the orbital state as there are the protons in the nuclei in a small region consisting of several molecules.

2.1 Simple Macroscopic Brain Model

An approximate spin model picture is illustrated here globally (Fig. 2.1) over the brain. The brain on the whole is electrically neutral as if it were a single atom. From this rudimentary equivalent over simplified picture to progress further towards reality one has to add regional perturbations in space and time. These are due to the local fine structure of individual atoms, molecules, tissues, fluids, etc., and the functions they perform. Then it will take the knowledge about brain science a step closer to the otherwise a very complex picture. In the regional areas there are various forces e.g. coulomb, nuclear, quantum, etc., which control the regional behavior in carrying out moment to moment brain functions. In a broad sense there is an overall system within the brain that looks after the intricate and wider functions of the brain. Figure 2.1 is a broad pictorial representation of the spin model of the brain. This is as if the orbiting electrons in molecules are circulating in copper coils and influence neighbors through self and mutual electrical induction.

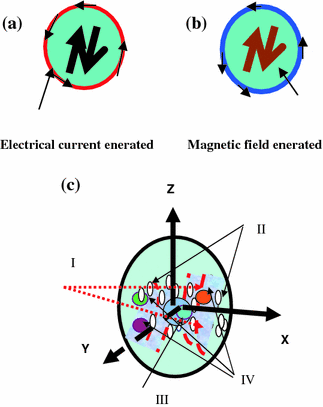
Fig. 2.1

a Electric current generated around the copper coil due to alternating magnetic field at the centre. b Alternating magnetic field generated at the centre of the coil due to alternating current flowing around the copper coil. a–c In this Figure is shown a pictorial depiction of an over simplified model of the brain. One can visualize a group of molecules (or macromolecules) in the brain under RF radiation behaving like copper coils carrying oscillating electrical current. This will lead to a generation of oscillating magnetic field through and around the molecules. The electromagnetic field created due to the RF radiation excitation encourages interaction between molecular dipole magnets. a, b Simple analogy to an experiment which can be conducted in a laboratory. It is a rough picture of a representation of the famous more than a century old copper coil experiment, by Hertz, the physicist, after whose name the unit of frequency of radiation Hz was adopted. c An approximate picture of a regional local order assumed present in pockets, in the brain, created by the internal magnetic field of around 1 Tesla, due to a group of nuclei, at a point. Small elliptical spots shown are examples of the several local micro-order regions in space. There is also an order on the global scale but is a weak one

The order can be regional as well as long range one. In the long (but on macro-molecular scale) range orbiting electrons are shown as a smeared out cloud as if they were a part of single giant molecule with single giant nucleus. But on this order is superimposed a regional (and long range) quantum-order due to quantum correlations between atoms and molecules. This order can be measured through multi-quantum coherence imaging from small voxels of 1 micron³ to 1 mm³ size. One can also mathematically model and get computational results and compare it with experiment. Both approaches where they will meet ultimately, to an agreement, will lead to the understanding of, the real, the unknown brain science. Thus there are four parts of the model of the brain as follows. I The effective internal surrounding magnetic field lines of force are imagined as if the whole brain were made of several macromolecular dipole magnet grouped with N–S poles. They interact quantum mechanically to produce long range orders. II The electrons as if belonging to a group of molecules as a unit surrounding the central positive nuclear charge of protons. III The filled ellipses represent sort of scattered short range ordered macromolecules submerged in the surrounding electron cloud depicted by unfilled circles. IV The giant nucleus of a local order is as if belonging to a group of macro-molecules as a unit in a local volume say a voxel.

The spatial density, ρ(x, y, z) variation of the spins can be worked out from the measured k space (k_x, k_y, k_z) intensity distribution in the MRI. The wave number in k-space, is given as, k = 1/λ, λ being the wavelength of the RF radiation. The measured k-space intensity variation (converted into the x-y-z space picture produced) has one to one correspondence to the spatial variation of spins density in the real (x, y, z) space in the brain. The density of spins (their number per unit volume) is related to the magnetic moment per unit volume created by the spins at a point. Due to the multinuclear structure of the brain the spin density sharply varies from point to point. The procedure of the transformation of the data form the k-space to the real space is a standard procedure well established in the conventional MRI. It is called as Fourier Transform Technique (FTT). It is a simple physics principle in electricity that an alternating current through a copper coil (Fig. 2.1a) induces an alternating magnetic field at the centre of the coil. This alternating magnetic field at the centre also influences a current in the same coil. This is called as the self induction. Similarly in a reverse manner an alternating magnetic field at the centre of a coil generates an alternating current through the coil and the generated current influences the magnetic field at the centre. Also a current in one coil induces a current in the neighboring coil which also generates a magnetic field at the centre of the second coil. This is called as the mutual induction. Atoms and molecules in our brain are a sort of copper coils with circulating electrons around the nucleus. The atomic orbits act like copper coils. The single electron in the outermost orbit of an atom is called as the valence electron. It has an intrinsic magnetic moment called as spin Sz = ± 1/2ђ. This is added to the atomic magnetic moment produced by the circulating electron in the orbit of an atom. One should remember that it is the valence electron in an atom that is the reactive one and creates interaction with its neighbors through its charge and spin. The Na–K pump which is the source of life in our brain is typical example of interest in this book. On the long range the influence on the neighbors in the short range is smeared out. This is what we get in conventional MRI. In the short range the quantum nature of the atom and the molecules can be seen. This is what QMRI is about.

In the real situation like the human brain in a small region of it referred to as a voxel the atoms and molecules overlap and the electron cloud charge spreads over a smeared out region. The shared electrons in a voxel represent signatures of the local interactions between the molecules, atoms, nuclei, as if there were a single large molecule and many electrons were bound to it due to the coupling between the electron spins. The overlapping electrons become a sort of shadow of the chemical structure in the local region. In the small region which may be spherically symmetric in regard to the distribution of spins the spin effects over-all cancel out. Thus there is no structural abnormality shown in the image of the region. The brain is thus a normal healthy one. If there is an asymmetry at a point due to say a tumor the symmetry is broken down and the spins appear as an outstanding spot in the MRI scan of the brain. This would be the most rudimentary form of image and is called as the chemical shift imaging (CSI). In this conventional MRI an RF pulse is applied along the X and Y directions perpendicular to the applied static magnetic field which is in the Z direction. A macroscopic average three dimensional spin asymmetry of the region can be projected as a planar asymmetry on the X–Y plane. In this plane the atomic spins evolve in time by interactions among themselves and the environment. The dynamics of the spins can be mapped in macro space and time to produce images of the local molecular events. One can venture now with the multi-quantum coherence technology newly emerging to explore spin dynamics in a multi-quantum regime. It is possible to look for quantum correlations among spins as a source of imaging rather than just be satisfied with the conventional topological echo planar imaging (EPI).

2.2 The Relationship Between the Angular Momentum L of the Orbiting Electron Around the Nucleus and the Associated Magnetic Moment μ_L

2.2.1 The Induced Electrical Signals Created by the Incident RF Radiation

An electron spins around its axis and thus has an intrinsic angular momentum referred to by symbol S. But the electron also orbits around the nucleus and thus there is an orbital momentum for the electron associated with the atom. It is referred to by the symbol L. Normally in an ensemble like human brain the intrinsic electron and atomic angular momentum are randomly oriented in space. They cancel themselves on a macroscopic scale. But on a microscopic scale the internal magnetic field of a group of nuclei makes the two types of angular momentum add up to produces a resultant J = L + S. It is called as the spin-orbit interaction. This is the result referring to a single electron and an atom in isolation with no atom to atom interactions (correlations). But in an ensemble like the brain there are around 10²³ (Avogadro number) nuclei including different species in a mole of the soft matter. Most of the spins in the absence of an applied (or internal) magnetic field cancel out in a small region say a voxel used for examination. In the presence of a magnetic field the spins have all their L′(multi-particle) and S′(multi-particle)s added up to produce a resultant J′ = L′ + S′.

Since an electron is a charged particle its rotation produces an electric current over the nano size area traced by it. This orbital motion of an electron in an orbit in the atom makes an atom a nano-magnet. There is an intrinsic relationship between angular momentum and the tiny magnet generated due to it. The product of the electric current i generated by the electron and the area of the orbit traced A is called as the magnetic dipole moment μ_l (=iA). In a very small volume of the order of tens and hundreds of nano meter³ the local nuclear magnetic field induces a resultant orientational force on magnetic moment μ_J as if trying to align the tiny magnet, along its own direction. The situation however enhances in the presence of an external applied magnetic field Hz₀.

In an externally applied field all the spins order themselves with their resultant magnetic moment tending to be pointing in the Hz₀ direction. The disturbance due to the local environment in which the spins are present however tend to disorient spins from the externally applied field direction and try to return them to their natural random behavior. The result is a compromise i.e. μ_J (the resultant magnetic moment corresponding to the total angular momentum J) rotates around the static magnetic field. The spin vector corresponding to it moves in a cone around the field. A single rotating vector around the static magnetic field Hz₀ is a representative of many spins grouped together as a bunch. Individual spins corresponding to different species of nuclei will rotate at different flip angles. But it is very hard to observe them on individual basis experimentally. It is the group effect that is observed.

One chooses to use a band of frequency of RF radiation to observe a small group of spins at a time. The tip of the spin (of a group corresponding to say a macromolecule) may be located anywhere at any moment in space and time. The angular momentum controls the position of the magnetic moment at any time. The angular momentum however can not be measured in a laboratory. The magnetic moment as a group representation can however be measured. On the scale of micrometer to mm to cm a large electrical signal is generated by the RF radiation. This signal created by the application of RF (radio frequency) radiation due to the magnetic spins vibration produces an electrical signal. An average magnetic moment per unit volume over a region is called as the magnetization of the soft matter. It is not constant over different points in space and its susceptibility to external RF radiation also varies in space and time. In fact this is what provides the secrets of the human brain science.

2.2.2 The Magnitude and the Quantum Nature of the Atomic Magnetic Moment

The angular momentum and the associated magnetic moment of the electrons and atoms are quantized. This means they can only occupy fixed quantum energy levels. In the process of transition above and down in the energy levels the energy is absorbed and re-radiated in quantum jumps, ΔJ = 0, ±1, ±2, …The angular momentum J and the magnetic moment μ_J are oppositely directed for an electron in an atom. Application at an angle θ of the RF pulse to the static field produces a rotation of spins by an angle θ from the static field. Normally θ = 90^° is used to rotate spin from Z-direction to say X or Y direction. These pulses are called as 90^° pulses. The static field exerts a torque τ on the spins. The torque is on the plane of an atomic orbit and it tries to orient the plane perpendicular to the static field and consequently keeps the spins in its own direction. RF pulse oscillations make the spins vibrate. Their vibration produces an electrical signal which is measured. By choosing suitable magnitude direction and frequency of the RF radiation applied the study of the quantum nature of the spins helps bring out the quantum secrets of the brain from the real time quantum images produced. Figure 2.2 is an approximate pictorial depiction of the macroscopic relationship between L and μ_L, in the presence of on externally applied magnetic field applied in the Z-direction.

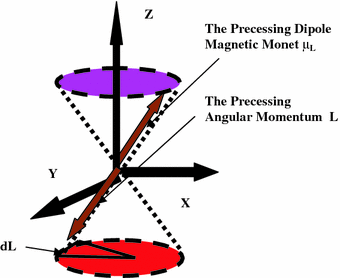
Fig. 2.2

The static magnetic field H₀ is applied along the Z-direction through the skull of the brain under scan. An electron being a charged particle produces an electric current in the orbit around the atom. This electric current say i when multiplied by the area A generated by the orbit is equal to the term called as the orbital dipole magnetic, μ_L = iA, of the atom. Normally μ_L is randomly oriented at any point in space and time in the absence of the field H_o. So the resultant effect overall is zero. H_o is perpendicular to the X–Y plane of the orbit and remains situated at the centre of the orbit

The angular momentum vector L of the orbiting electron that produces the magnetic moment is not static in space along the Z-direction. It is under precession at an angle θ to the static magnetic field. This happens because though the spins are under force to remain oriented in the Z-direction the local activities, e.g. metabolism, neurotransmission, etc., try to keep the spins oriented, away from the Z-axis. This results in an equilibrium i.e. the precession of the spins at an angle θ to the Z-axis. The length of the vector of the angular momentum L i.e. its magnitude remains fixed for a particular frequency of resonance and amplitude of the RF radiation. However as a result of the precession in space its direction is changing at the rate of a fixed angular frequency. Due to the quantum nature of the angular momentum a fixed quantum of energy is supplied by H₀, i.e. E = μ_L H₀ cosθ. Here θ is the angle between μ_L and H₀. L remains quantized in space. But it rotates around H₀ in random fashion i.e. it can be anywhere in X–Y plane at any time. It can change its values up and down in quantum jumps. The magnitude of the jump is L_z = ћm_z, where m_z is the magnetic quantum number with values, ± (0, 1, 2, …) and ћ is the angular Planck constant. The tip of L moves in a circle generating a cone around H₀. This angular momentum cone generated is shown in the lower part of the diagram (Fig. 2.2). Since the magnetic moment is oppositely directed to the angular momentum due to the negative charge of the electron the corresponding cone generated by the magnetic moment is shown in the upper part of the diagram (Fig. 2.2).

The rotation of the angular momentum L in a circle is due to the precession of the magnetic moment μ_l. The precession frequency is referred to by the symbol Ω. The orbital magnetic moment of the electron is given as μ_l = g_l (μ_bL/ђ). It is coupled to the angular momentum and rotates at the same frequency. The precessional frequency Ω of the spin magnetic moment μ_l is given as Ω = g_l (μ_bH₀/ђ). g_l = orbital spectroscopy splitting factor. μ_b = (eђ/2m_e) = 0.927 × 10⁻²³ amp-m² (or Joules/Tesla) is the fundamental unit of the dipole magnetic moment μ_l, m_e being the mass of the electron and e its charge. In a multi-particle system one deals with total spectroscopy splitting factor g_J. An electron in an atomic orbit is also rotating around its own axis. It is called as the intrinsic angular momentum (spin) of the electron S. In the presence of the field H₀ there is the resultant angular momentum J = L + S of the atom which one need to consider. The brain ensemble is a hetero-nuclear one. In a small volume one need to take some kind of an average of the magnetic moments and also in regard to the resultant angular momentum J. The ratio of the magnetic moment to the angular momentum is called as the gyro-magnetic ration GMR. The GMR = (μ_J/J) = g_J (μ_b/ħ). Here μ_b is the fundamental unit of the magnetic moment and ħ provides the fundamental unit of energy (has units of joules second) and is called as the Planck’s constant of the RF radiation, g_l is the resultant spectroscopic splitting factor. This ratio has very important place in the MRI literature. There are many species (hetero-nuclear situation) of nuclei in a small selected volume in the brain. For examination one needs to take into account the resultant effect of all the local interactions among the nuclei. It is a common practice now to take spectroscopy of a small region of say mm³ – cm³ dimension as part of MRI. This small volume is referred to as a voxel in the medical MRI literature.

Spectroscopy is very helpful in determination of the distribution in space of the relative and absolute metabolic concentration in the brain. The spectroscopy also helps in the diagnostics of the brain tumors. The precessional frequency of the magnetic spins around H₀ is Ω = g_J (μ_bH₀/ђ). Here g_J is the spectroscopy splitting factor that determines the splitting of the energy levels in a voxel and is a measure of the distribution of the metabolite concentrations. In Fig. 2.2 there is only a rough depiction of the precession of the diamagnetic dipole moment. The μ_l shown is representative of a single electron or a proton. In fact it can very well be the resultant of several neighboring electrons and protons. Furthermore in a small selected region i.e. a voxel in the brain for imaging the outer orbital electrons in the neighboring molecules and the protons in the nuclei will all couple together to produces a resultant angular momentum J = L + S. Here L precisely could be the resultant of angular momentum of atomic angular momentum and that of the nuclear one. The over all S would be the intrinsic angular momentum of outermost orbital electrons in the neighboring molecules. In larger size voxels diffusion dynamics of the molecules modulates the received signal.

It is part of the space and time functional dependence of the fluids e.g. blood circulation on the angular momentum J. A typical example where the spin dynamics can be seen in action is the BOLD (blood oxygen level dependent)-MRI. One should always remember that it is not the angular momentum J that is a measurable quantity. Instead it is the changes associated with the precession frequency of the magnetic moment and the phase (time of arrival of signals) due to varying angles between spins created by the RF radiation that is measured. Finally the received modulated radiation is the consequence of the variations of the magnetic dipole moment which oscillates because of the precession of the angular momentum J. According to the simple physics principles of dynamic electricity an oscillating magnet in space produces electrical signals around it. Its space and time variation detected by the sensor forms the image.

Only gold members can continue reading. Log In or Register to continue