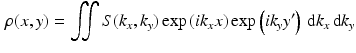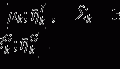field inhomogeneities and the uneven magnetisation of the brain due to its magnetic susceptibility can lead to spatial displacements of several pixels. This prevents comparison between these images and others that do not contain these artefacts, such as T1- and T2-weighted images. Some artefacts lead to spatial offsets between the DW-MR images in a dataset, which compromises their anatomical correspondence and undermines the estimates of microstructure obtained from them. For example, motion can lead to rigid offsets between images, and eddy currents lead to a shear, scaling and translation of the image in the phase encoding (PE) direction that varies according to the amount of diffusion sensitisation used (typically summarised by the b-value) and the direction it is applied in.
Techniques for dealing with these artefacts can broadly be divided into those implemented at acquisition time, involving either some modification to the acquisition process or the collection of supplementary data, and post-processing methods implemented after acquisition time. Post-processing techniques are the most widely used, as they have several advantages: they can be applied retrospectively to already acquired data, a user can revert to the original data if the technique does not work as hoped, and they don’t require additional scan-time, which is often expensive.
The literature contains a vast body of post-processing techniques and software packages for correcting artefacts in DW-MRI [
4–
6]. Ideally their corrections would be validated by comparison to the ground truth, i.e. a map of the spatial deformations caused by the artefacts, but these cannot be obtained for real data. As a result the literature relies on either qualitative visual assessments of image alignment [
7], or quantitative assessments of surrogate measures of alignment that have questionable validity, such as tract length [
8], or reduced residuals from fits to microstructural models [
9]. The lack of an objective ground truth means existing techniques cannot be systematically assessed, preventing end-users from making an informed choice. The development of new methods is also hindered, as any improvements over existing ones are difficult to demonstrate.
Simulation could provide us with a ground truth that would enable us to assess methods objectively, allowing researchers to make informed decisions when selecting post-processing methods. Simulation systems exist for MRI [
10,
11] but there is nothing satisfactory for DW-MRI. Several systems are designed to simulate DWIs of white matter bundles [
12] but these are unable to generate the full brain images required for the assessment of post-processing methods. Methods that do attempt to simulate full-brain DWIs exhibit at least one of two serious limitations. The first is the failure to model the full process of image acquisition [
13], i.e. the recording of a signal in frequency space which is Fourier transformed to generate a spatial image, which precludes the inclusion of realistic artefacts. The second is the use of a heavily simplified model to create the DW contrast, which means the simulations do not capture some of the features of DWIs that makes their processing uniquely challenging, such as the variation of contrast with the direction of diffusion weighting [
14].
In this work we introduce a simulation framework that allows for realistic DW-MR images to be generated, enabling the effectiveness of correction techniques to be assessed objectively and directly. The framework simulates the physics of MRI acquisition by solving Bloch’s and Maxwell’s equations, which ensures the images and their artefacts capture the key features of their real-world counterparts. The complexity of diffusion contrast is captured using a model-based approach. The framework is flexible, and allows for a range of artefacts to be modelled including EC, motion, B
inhomogeneities and magnetic susceptibility. We demonstrate an application of this framework to EC artefacts, by providing a quantitative assessment of the most commonly used correction technique, registration of all DWIs to b = 0.
2 Methods
In this section we describe our simulation framework for producing realistic DW-MR images, and discuss its application to validating eddy-current correction schemes. An overview of the framework is discussed in Sect.
2.1, our implementation of it in Sect.
2.2 and its application in Sect.
2.3.
2.1 Simulation Framework
The framework (Fig.
1) combines a physics-based approach to the MR image acquisition process with a model-based representation of diffusion in order to simulate realistic DW-MR datasets. To provide a meaningful validation a simulation must capture the key characteristics of DW-MR images and their artefacts. Many of the artefacts are introduced during the acquisition of the MR signal in k-space, so it is necessary to reproduce this process for a faithful simulation.
The framework takes four main inputs. The first is a geometric object that specifies the proton density and location of white matter (WM), grey matter (GM) and cerebrospinal fluid (CSF) along with their T1 and T2 values. The second is a representation of diffusion-weighting. These two inputs are combined to produce a geometric object with its proton density reduced by an attenuation factor determined by the diffusion model. The third input is a pulse sequence, detailing the RF pulses and gradients. The fourth are details of any artefacts to be included, e.g. motion. The effects of eddy currents are included in the pulse sequence. The MR simulator takes the attenuated object, pulse sequence and artefacts and solves Bloch’s and Maxwell’s equations at each point in the object, summing the resultant signal in order to generate the k-space measurements. This is Fourier transformed to produce the output DWI.
2.2 Implementation
A full-brain segmentation was used as the geometric object input. It was created with T1- and T2-weighted images from a single subject from the WU-Minn HCP dataset [
15], using FSL’s FAST [
16]. Diffusion weighting was achieved using the diffusion tensor (DT) [
17]. Although the DT can not faithfully represent complex WM anatomy, such as crossing fibres, empirically we find it adequate for capturing the main features that make the processing of DWIs particularly challenging: the contrast between WM, GM and CSF, as well as the variation of signal with both the direction and strength of diffusion weighting (see Fig.
3). To account for the departure from Gaussian diffusion at higher
b-values, separate tensors were fit to the b = 1000 s mm
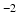
and b = 2000 s mm
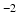
DWIs in the HCP dataset using FSL’s DTIFIT. The tensor from the b = 1000 s mm
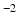
shell was used to predict attenuation for simulated DWIs with
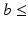
1000 s mm
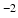
, and the tensor from the b = 2000 s mm
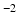
shell was used for simulations with
b-values above this.
Eddy currents were added to the pulse sequence using the method in [
14], by superposing a sum of decaying exponentials on each gradient field:
where
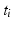
corresponds to the time each diffusion gradient is turned on or off,
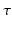
is the decay time,
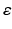
is a constant determining the relationship between the strength of eddy and diffusion gradients and a + or – is selected depending on whether the gradient is being turned on or off. We performed simulations with
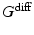
= 40 m T m
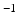
, and selected
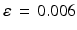
and
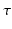
= 100 ms to represent typical values found in a clinical scanner [
9].
We used POSSUM [
11] to simulate the physics of MR acquisition. POSSUM allows for the creation of pulse sequences, signal generation and image reconstruction. By solving for the magnetization vectors over time at every voxel in the object it allows for effects such as spin history, motion during pulse readout and B
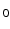
inhomogeneities to be accounted for. By default, POSSUM simulates gradient-echo echo-planar imaging (EPI) sequences. To simulate the spin-echo EPI sequences typically used for DWI acquisition, we replace the default tissue-specific T
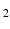
* values with their corresponding T
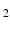
values.
2.3 Application to Eddy-Current Artefacts
To demonstrate the application of our framework we use it to assess one of the most routinely employed methods for EC correction, registration of all DWIs to b = 0, by comparing evaluated and ground truth displacement fields.
Comparison of spatial displacement fields is the most direct way to evaluate post-processing methods. For the case of EC distortions, we obtain a mapping from distorted to undistorted space from an analysis of how the influence of eddy currents on k-space translates into geometric distortions in image space. The relationship between k-space and image space is expressed as a Fourier transform:
where
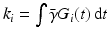
,
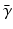
is the gyromagnetic ratio,
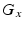
and
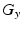
are the imaging gradients applied,
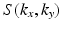
is the MR signal in k-space, and
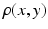
is the image in real space. In the presence of eddy currents, our imaging gradients are modified by additional gradients
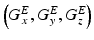
and a spatially invariant term
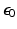
, causing our phase term to become modified. Assuming the phase-encoding (PE) direction is aligned with the
y-axis, our signal equation becomes [
9]:
Get Clinical Tree app for offline access

 inhomogeneities and magnetic susceptibility. We demonstrate an application of this framework to EC artefacts, by providing a quantitative assessment of the most commonly used correction technique, registration of all DWIs to b = 0.
inhomogeneities and magnetic susceptibility. We demonstrate an application of this framework to EC artefacts, by providing a quantitative assessment of the most commonly used correction technique, registration of all DWIs to b = 0.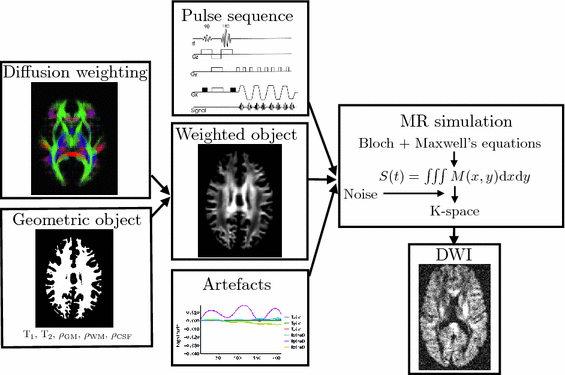
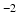 and b = 2000 s mm
and b = 2000 s mm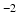 DWIs in the HCP dataset using FSL’s DTIFIT. The tensor from the b = 1000 s mm
DWIs in the HCP dataset using FSL’s DTIFIT. The tensor from the b = 1000 s mm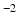 shell was used to predict attenuation for simulated DWIs with
shell was used to predict attenuation for simulated DWIs with 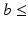 1000 s mm
1000 s mm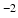 , and the tensor from the b = 2000 s mm
, and the tensor from the b = 2000 s mm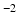 shell was used for simulations with b-values above this.
shell was used for simulations with b-values above this.![$$\begin{aligned} G_{x,y,z}^{\mathrm {E}}=\sum _{i}^{} \pm \varepsilon \, G^{\mathrm {diff}}_{x,y,z}\exp \left[ {-(t-t_i)/ \tau }\right] \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_50_Chapter_Equ1.gif)
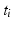 corresponds to the time each diffusion gradient is turned on or off,
corresponds to the time each diffusion gradient is turned on or off, 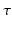 is the decay time,
is the decay time, 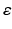 is a constant determining the relationship between the strength of eddy and diffusion gradients and a + or – is selected depending on whether the gradient is being turned on or off. We performed simulations with
is a constant determining the relationship between the strength of eddy and diffusion gradients and a + or – is selected depending on whether the gradient is being turned on or off. We performed simulations with 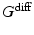 = 40 m T m
= 40 m T m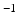 , and selected
, and selected 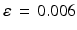 and
and 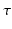 = 100 ms to represent typical values found in a clinical scanner [9].
= 100 ms to represent typical values found in a clinical scanner [9]. inhomogeneities to be accounted for. By default, POSSUM simulates gradient-echo echo-planar imaging (EPI) sequences. To simulate the spin-echo EPI sequences typically used for DWI acquisition, we replace the default tissue-specific T
inhomogeneities to be accounted for. By default, POSSUM simulates gradient-echo echo-planar imaging (EPI) sequences. To simulate the spin-echo EPI sequences typically used for DWI acquisition, we replace the default tissue-specific T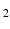 * values with their corresponding T
* values with their corresponding T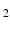 values.
values.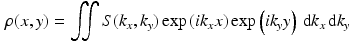
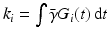 ,
, 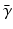 is the gyromagnetic ratio,
is the gyromagnetic ratio, 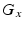 and
and 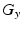 are the imaging gradients applied,
are the imaging gradients applied, 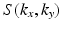 is the MR signal in k-space, and
is the MR signal in k-space, and 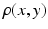 is the image in real space. In the presence of eddy currents, our imaging gradients are modified by additional gradients
is the image in real space. In the presence of eddy currents, our imaging gradients are modified by additional gradients 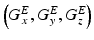 and a spatially invariant term
and a spatially invariant term 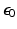 , causing our phase term to become modified. Assuming the phase-encoding (PE) direction is aligned with the y-axis, our signal equation becomes [9]:
, causing our phase term to become modified. Assuming the phase-encoding (PE) direction is aligned with the y-axis, our signal equation becomes [9]: