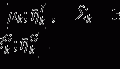better reproducibility compared to existing approaches. We also report that our group-wise parcellations are functionally more consistent, thus, can be reliably used to represent the population in network analyses.
1 Introduction
The human cerebral cortex is assembled into subregions that interact with each other in order to coordinate the neural system. Identification of these subregions is critical for a better understanding of the functional organization of the human brain and to reveal the connections of underlying subsystems [19]. Functional connectivity studies have identified several subsystems, each of which is spanned across different cortical areas and associated with a specific functional ability [16]. This has further advanced the analysis of the functional architecture of the brain by constructing graphical models of the connections within individual subsystems and their interactions with each other at different levels of detail [14, 25]. Analysis of these networks is also important for deriving biomarkers of neurological disorders such as Alzheimer’s disease [20] and schizophrenia [1].
In this paper, our main motivation is to identify functionally homogeneous and spatially continuous cortical subregions which can be used as the network nodes for a whole-brain connectivity analysis. In a typical network analysis, nodes are usually represented by the average signal within each cortical subregion, which is further beneficial to improve the SNR [9]. A good parcellation framework should be capable of grouping cortical regions with similar functional patterns together, thus the average signal can effectively represent each part of the subregion. It is also highly critical to generate a reliable group-wise representation that reflects the common functional characteristics of the community, yet is tolerant to changes in the functional organization at the single-subject level that may emerge due to functional and anatomical differences across subjects.
Our proposed method is based on connectivity patterns captured from resting-state functional magnetic resonance imaging (rs-fMRI) data. Rs-fMRI records neurocognitive activity by measuring the fluctuations in the blood oxygen level signals (BOLD) in the brain while the subject is at wakeful rest. Since the brain is still active in the absence of external stimuli, these fluctuations can be used to identify the cerebral functional connections [4]. On the other hand, task-based fMRI parcellations driven by neuropsychological studies, e.g. language task [12], target specific subregions in the cortex in order to investigate their functional organization, but ignores the activation from the non-target areas, which makes them incapable for the whole-brain network analyses. Similarly, anatomical parcellations generated from cytoarchitectonic atlases [22] are not able to capture the functional organization of the brain. This can be attributed to the fact that cytoarchitecture of the cerebral cortex does not necessarily require to be consistent with the functional connectivity patterns [12, 21] and arbitrary parts of the same cytoarchitectonic region can exhibit structural and functional variability [6]. Nevertheless, parcellating the cerebral cortex based on resting-state correlations can potentially identify functional organization of the cerebral cortex without the knowledge of the cytoarchitecture and an external stimulus or a cognitive process [18].
The rs-fMRI-based cortical parcellation literature consists of methods that subdivide the cerebral cortex into different number of subregions according to the requirements of the applications and topological network features across the cerebral cortex [15]. These methods are based on but not limited to independent component analysis (ICA) [2], region growing [5, 24], spectral graph theory [6, 14, 17], boundary mapping [9], k-means clustering [3, 8] and hierarchical clustering [11, 23]. Some of these techniques [2, 3, 14, 25] parcellate the cortex at a very coarse level (less than hundred subregions), with the aim of identifying resting-state networks spanning across the cortex or some fractions of it. Because of the aforementioned risks of having non-uniform functional patterns within subregions, these parcellations cannot be reliably used for network node identification. Other methods typically generate a few hundred clusters without losing the ability of representing the functional organization of the cortex. The most critical issue that is not addressed by these techniques is the adaptability of group representation to individual single subjects. The group-wise parcellations generated from a set of subjects are generally assumed to represent the whole group. However, due to functional and structural variations at the single-subject level, it is very unlikely that a group parcellation would highly match with single-level parcellations [9].
We address this problem and introduce a new parcellation framework which is capable of both generating group-wise and single-level parcellations from a joint graphical model. To this end, we make use of spectral graph decomposition techniques and represent the population in a multi-layer graph which effectively captures the fundamental properties of the whole group as well as preserves individual subject characteristics. We show that the parcellations obtained in this setting are (a) more reproducible across different groups of subjects and (b) better reflect functional and topological features shared by multiple subjects in the group compared to other parcellation methods. These aspects of the proposed method differentiate it from the previous parcellation algorithms and constitute our main contributions in this paper. Finally, our framework can be used to generate parcellations with different number of subregions, allowing users to conduct a network analysis at different levels of detail.
2 Methodology
2.1 Data Acquisition and Preprocessing
We evaluate our algorithm using data from the WU-Minn Human Connectome Project (HCP). We conducted our experiments on the rs-fMRI datasets, containing scans from 40 different unrelated subjects (22 female, 18 male healthy adults, ages 22–35). The data for each subject was acquired in two sessions, divided into four runs of approximately 15 min each. During the scans, subjects were presented a fixation crosshair, projected against a dark background, which prevented them from falling asleep. The dataset was preprocessed and denoised by the HCP structural and functional minimal preprocessing pipelines [7]. The final result of the pipeline is a standard set of cortical time courses which have been registered across subjects to establish correspondences. This was achieved by mapping the cortical gray matter voxels to the native cortical surface and registering them onto the 32k standard triangulated mesh. Following the preprocessing step, each time course was temporally normalized to zero-mean and unit-variance. We concatenated the time courses of each scan, obtaining an almost 60-minute rs-fMRI data for each of the 40 subjects and used them to evaluate our approach.
2.2 Joint Spectral Decomposition
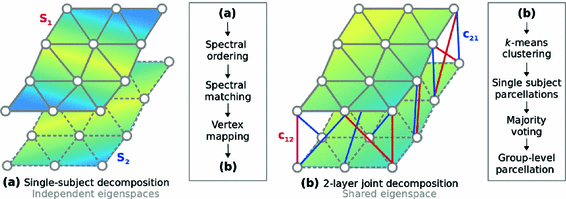
We propose a clustering approach based on spectral decomposition to identify whole-cortex parcellations that can effectively capture the functional associations across multiple subjects. At the single-subject level, the cerebral cortex is represented as an adjacency matrix, in which the functional correlations are encoded as edge weights. Each adjacency matrix is transformed to the spectral domain via an eigenspace decomposition. The corresponding eigenvectors are combined into a multi-layer graph, which is capable of representing the fundamental properties of the underlying functional organization of individual subjects. Similar to the single-level graph decomposition, this joint multi-layer graph can then be decomposed into its eigenvectors, creating a feature matrix in the spectral domain that can be fed into a clustering algorithm, e.g. k-means, for grouping each vertex into a subregion, hence producing the final parcellations. A visual summary of the approach is given in Fig. 1.
Sparse Adjacency Matrix. The cerebral cortex of the brain is represented as a smooth, triangulated mesh with no topological defects. We model the mesh vertices and their associations as a weighted graph 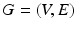 , where V is the set of vertices (nodes) and E is the set of edges connecting them. Here we enforce a spatial constraint and construct an edge between two vertices if and only if they are adjacent to each other. This spatial constraint results in a sparse adjacency matrix with two benefits: (a) it ensures that resulting clusters are spatially continuous and (b) it reduces the computational overhead during the spectral decomposition of the graph. Finally, the edge weights between the adjacent vertices are set to the Pearson product-moment correlation coefficients of their rs-fMRI time courses (after discarding negative correlations and applying Fisher’s z-transformation) and represented as an
, where V is the set of vertices (nodes) and E is the set of edges connecting them. Here we enforce a spatial constraint and construct an edge between two vertices if and only if they are adjacent to each other. This spatial constraint results in a sparse adjacency matrix with two benefits: (a) it ensures that resulting clusters are spatially continuous and (b) it reduces the computational overhead during the spectral decomposition of the graph. Finally, the edge weights between the adjacent vertices are set to the Pearson product-moment correlation coefficients of their rs-fMRI time courses (after discarding negative correlations and applying Fisher’s z-transformation) and represented as an 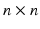 weighted adjacency matrix W, where n is the number of vertices on the cortex.
weighted adjacency matrix W, where n is the number of vertices on the cortex.
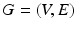 , where V is the set of vertices (nodes) and E is the set of edges connecting them. Here we enforce a spatial constraint and construct an edge between two vertices if and only if they are adjacent to each other. This spatial constraint results in a sparse adjacency matrix with two benefits: (a) it ensures that resulting clusters are spatially continuous and (b) it reduces the computational overhead during the spectral decomposition of the graph. Finally, the edge weights between the adjacent vertices are set to the Pearson product-moment correlation coefficients of their rs-fMRI time courses (after discarding negative correlations and applying Fisher’s z-transformation) and represented as an
, where V is the set of vertices (nodes) and E is the set of edges connecting them. Here we enforce a spatial constraint and construct an edge between two vertices if and only if they are adjacent to each other. This spatial constraint results in a sparse adjacency matrix with two benefits: (a) it ensures that resulting clusters are spatially continuous and (b) it reduces the computational overhead during the spectral decomposition of the graph. Finally, the edge weights between the adjacent vertices are set to the Pearson product-moment correlation coefficients of their rs-fMRI time courses (after discarding negative correlations and applying Fisher’s z-transformation) and represented as an 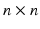 weighted adjacency matrix W, where n is the number of vertices on the cortex.
weighted adjacency matrix W, where n is the number of vertices on the cortex.Spectral Decomposition. Given the adjacency matrix W, the graph Laplacian can be computed as 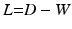 , where
, where 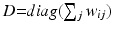 is the degree matrix of W. L is a diagonalizable matrix which can be factorized as
is the degree matrix of W. L is a diagonalizable matrix which can be factorized as 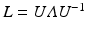 , where
, where 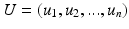 is the eigensystem, with
is the eigensystem, with 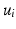 representing each eigenvector and
representing each eigenvector and 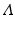 is a diagonal matrix that contains the eigenvalues, represented as
is a diagonal matrix that contains the eigenvalues, represented as 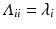 . Eigenvectors are powerful tools in terms of encapsulating valuable information extracted from the decomposed matrix in a lower dimension. In particular, after sorting the eigenvalues as
. Eigenvectors are powerful tools in terms of encapsulating valuable information extracted from the decomposed matrix in a lower dimension. In particular, after sorting the eigenvalues as 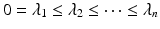 and organizing the corresponding eigenvectors accordingly, the first k eigenvectors denoted as the spectral feature matrix
and organizing the corresponding eigenvectors accordingly, the first k eigenvectors denoted as the spectral feature matrix 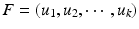 are capable of representing the most important characteristics of the decomposed matrix. Thus, each vertex on the cortical surface can be represented by its corresponding row in F, without losing any critical information.
are capable of representing the most important characteristics of the decomposed matrix. Thus, each vertex on the cortical surface can be represented by its corresponding row in F, without losing any critical information.
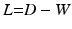 , where
, where 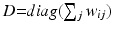 is the degree matrix of W. L is a diagonalizable matrix which can be factorized as
is the degree matrix of W. L is a diagonalizable matrix which can be factorized as 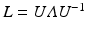 , where
, where 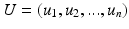 is the eigensystem, with
is the eigensystem, with 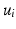 representing each eigenvector and
representing each eigenvector and 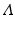 is a diagonal matrix that contains the eigenvalues, represented as
is a diagonal matrix that contains the eigenvalues, represented as 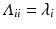 . Eigenvectors are powerful tools in terms of encapsulating valuable information extracted from the decomposed matrix in a lower dimension. In particular, after sorting the eigenvalues as
. Eigenvectors are powerful tools in terms of encapsulating valuable information extracted from the decomposed matrix in a lower dimension. In particular, after sorting the eigenvalues as 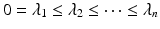 and organizing the corresponding eigenvectors accordingly, the first k eigenvectors denoted as the spectral feature matrix
and organizing the corresponding eigenvectors accordingly, the first k eigenvectors denoted as the spectral feature matrix 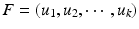 are capable of representing the most important characteristics of the decomposed matrix. Thus, each vertex on the cortical surface can be represented by its corresponding row in F, without losing any critical information.
are capable of representing the most important characteristics of the decomposed matrix. Thus, each vertex on the cortical surface can be represented by its corresponding row in F, without losing any critical information.
Fig. 1.
Visual representation of the parcellation pipelines with an emphasis on (a) single-subject and (b) joint spectral decomposition, illustrated on the patches cropped from the cortical surfaces 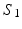 and
and 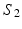 . The red and blue edges correspond to the mappings
. The red and blue edges correspond to the mappings 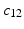 and
and 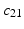 , obtained by matching the closest vertices in
, obtained by matching the closest vertices in 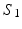 and
and 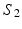 , respectively (Color figure online).
, respectively (Color figure online).
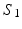 and
and 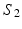 . The red and blue edges correspond to the mappings
. The red and blue edges correspond to the mappings 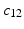 and
and 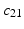 , obtained by matching the closest vertices in
, obtained by matching the closest vertices in 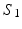 and
and 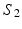 , respectively (Color figure online).
, respectively (Color figure online).Spectral Matching. The idea of spectral matching is finding the closest vertex pairs in two eigensystems by comparing their eigenvectors in the spectral feature matrices [13]. The observations on the cortical surfaces transformed to the spectral domain revealed that eigenvectors show very similar characteristics across subjects. This attribute can be utilized to obtain a common eigensystem that reflects structural and functional features shared by the subjects in the group, while also preserving individual subject characteristics.
Notably, the same cortical information represented with the eigenvector 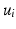 in
in 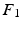 can be decoded in the eigenvector
can be decoded in the eigenvector 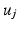 in
in 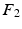 , without the necessity of being in the same order or having the same sign. Therefore, an additional correction must be carried out in order to find the corresponding eigenvectors on both cortical surfaces before applying spectral matching. To this end, we make use of a simple spectral ordering technique, where for each eigenvector
, without the necessity of being in the same order or having the same sign. Therefore, an additional correction must be carried out in order to find the corresponding eigenvectors on both cortical surfaces before applying spectral matching. To this end, we make use of a simple spectral ordering technique, where for each eigenvector 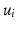 in
in 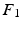 we compute its closest eigenvector
we compute its closest eigenvector 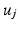 in
in 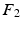 using Euclidean distance and if
using Euclidean distance and if 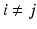 we mark
we mark 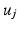 for re-ordering. We then take another iteration and repeat the same process after flipping the signs of each eigenvector in
for re-ordering. We then take another iteration and repeat the same process after flipping the signs of each eigenvector in 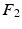 and if a closer match is found, the new eigenvector is marked and its new sign is preserved throughout the sequential processes. Finally, the marked eigenvectors in
and if a closer match is found, the new eigenvector is marked and its new sign is preserved throughout the sequential processes. Finally, the marked eigenvectors in 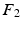 are re-ordered accordingly.
are re-ordered accordingly.
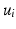 in
in 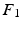 can be decoded in the eigenvector
can be decoded in the eigenvector 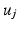 in
in 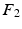 , without the necessity of being in the same order or having the same sign. Therefore, an additional correction must be carried out in order to find the corresponding eigenvectors on both cortical surfaces before applying spectral matching. To this end, we make use of a simple spectral ordering technique, where for each eigenvector
, without the necessity of being in the same order or having the same sign. Therefore, an additional correction must be carried out in order to find the corresponding eigenvectors on both cortical surfaces before applying spectral matching. To this end, we make use of a simple spectral ordering technique, where for each eigenvector 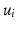 in
in 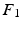 we compute its closest eigenvector
we compute its closest eigenvector 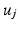 in
in 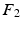 using Euclidean distance and if
using Euclidean distance and if 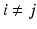 we mark
we mark 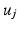 for re-ordering. We then take another iteration and repeat the same process after flipping the signs of each eigenvector in
for re-ordering. We then take another iteration and repeat the same process after flipping the signs of each eigenvector in 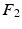 and if a closer match is found, the new eigenvector is marked and its new sign is preserved throughout the sequential processes. Finally, the marked eigenvectors in
and if a closer match is found, the new eigenvector is marked and its new sign is preserved throughout the sequential processes. Finally, the marked eigenvectors in 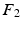 are re-ordered accordingly.
are re-ordered accordingly.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree