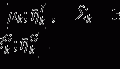(1)
where ◦ denotes element-wise multiplication. (1) has been shown to provide local maxima of the following non-convex optimization problem [17]:
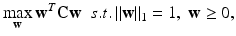
(2)
2.2 Coupled Replicator Dynamics
Separating C into d × d genotype fitness matrices F for females and M for males to model sex differences, the survival probabilities of the alleles in the female gene pool, p(k), and in male gene pool, q(k), based on natural selection can be estimated using the following multiplicative updates [14]:
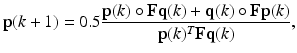
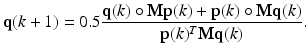
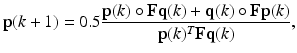
(3)
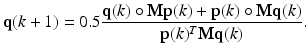
(4)
Analogous to RD, F and M are assumed to be real, symmetric, and non-negative. The non-negativity constraint enforces p( k) and q(k) to be ≥ 0. Also, Σ j p j (k) = 1 since 0.5∙Σ j (p j (k)(Fq(k)) j + q j (k)(Fp(k)) j ) = 0.5(p(k)T Fq(k) + q(k)T Fp(k)) = 0.5(p(k)T Fq(k) + p(k)T Fq(k)) = p(k)T Fq(k), where we have exerted the property that a scalar and its transpose are equal, i.e. q(k)T Fp(k) = p(k)T Fq(k). Similarly, Σ j q j (k) = 1. Thus, by matching the denominator of (3) and (4) with that of (1), one can see that (3) and (4) together form a local maximizer of the following optimization problem:
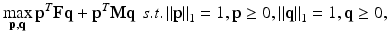
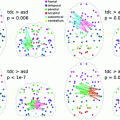
where the l 1 constraint on p and q enforces sparsity. Since p is multiplied to both F and M in (5), the optimal p would jointly account for the genotype fitness of both sexes, and the same goes for q. This coupling property of CRD can be more clearly seen by examining (3) and (4). Specifically, information in M is propagated to p through q, and vice versa. We note that CRD also uses mutual similarity as the criterion for grouping nodes, which can be proved in a similar manner as in the case of RD. Further, we highlight that the sparsity patterns of p and q tend to perfectly match upon convergence for dense graphs. Specifically, assume p i (k) = 0 upon convergence. Based on (3), this implies p i (k)∘Fq i (k) + q i (k)∘Fp i (k) = 0. p i (k)∘Fq i (k) must equal 0 since p i (k) = 0, thus q i (k)∘Fp i (k) must also equal 0. This condition is satisfied only if q i (k) = 0 or Fp i (k) = 0. Fp i (k) = 0 requires F ij to be exactly zero for each surviving allele j. In both our synthetic and real data, F is never sparse enough to warrant this condition. Hence, q i (k)◦Fp i (k) = 0 can only arise by having q i (k) = 0, which enforces p and q to have the same sparsity patterns. The nodes in the identified subnetwork are thus given by the nonzero elements of either p or q. Again, other subnetworks can be found by reapplying (3) and (4) after removing the nodes of the identified subnetworks from the graphs. However, this strategy modifies the original graph structure, thereby affecting the remaining local maxima. We describe a more principled way of identifying the other subnetworks that permits subnetwork overlaps and preserves the location of the remaining local maxima in Sect. 2.4.
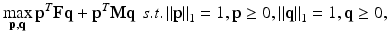
(5)
2.3 Coupled Stable Replicator Dynamics
Graph Incrementation. Sparsity of the subnetworks identified by CRD is intrinsically determined based on the mutual similarity among nodes. This property is desirable under the ideal case of noiseless graphs. In practice, such a strict criterion for grouping nodes could easily result in a subnetwork being falsely split into components [19], since even small perturbations to F and M would render certain nodes non-mutually connected. To reduce this effect, one strategy is to add a constant, η, to the off-diagonal elements of F and M [15]. This strategy artificially increases the mutual similarity among all nodes and swamps the differences between elements of F (and M) that are considerably smaller than η. We can hence adjust the sparsity level of the identified subnetworks by changing η. Choosing the optimal η is non-trivial. Also, noise in F and M could result in false nodes being included in the subnetworks. To jointly deal with these problems, we present next a procedure for integrating stability selection into CRD.
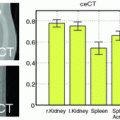
Stability Selection. The idea behind stability selection is that if we bootstrap the data many times and perform subnetwork identification on each bootstrap sample, nodes that truly belong to the same subnetwork are likely to be jointly selected over a large fraction of bootstrap samples, whereas false nodes are unlikely to be persistently selected [16]. To incorporate stability selection in refining each subnetwork identified by CRD, we first generate a set of matrices {F η } by adding η to the off-diagonal elements of F. A range of η from 0 to d∙max ij |F ij | at a step size of κ is used, where κ is chosen small enough to ensure that no more than one node is added to a subnetwork at each increment of η. The same procedure is applied to M to generate {M η }.We then apply CRD to each (F η , M η ) pair with p(0) and q(0) set to the CRD solution of the previous η increment (with 1/d added to all elements and renormalized to sum to 1), which enforces CRD to converge to a local maximum in the vicinity of the previous η increment for retaining subnetwork correspondence. We note that adding 1/d is critical since zeros in p(k) and q(k) remain as zeros as (3) and (4) are iterated, which prohibits new nodes from being added. We discard subnetworks that contain more than 10 % of the nodes assuming a subnetwork would not span more than 10 % of the brain. Next, we generate 100 bootstrap samples of F and M (as explained in Sect. 2.5), and compute 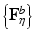 and
and 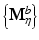 from each bootstrap sample F b and M b . We then apply CRD on each
from each bootstrap sample F b and M b . We then apply CRD on each 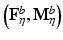 pair. For each η, we estimate the selection probability of each node as the proportion of bootstrap samples in which the given node attains a nonzero weight [16]. This estimation can be done based on either p or q since their sparsity patterns perfectly match. Finally, we threshold the selection probabilities to identify nodes that belong to the same subnetwork. A threshold τ that bounds the expected number of false nodes in a subnetwork, E, is given by [16]:
pair. For each η, we estimate the selection probability of each node as the proportion of bootstrap samples in which the given node attains a nonzero weight [16]. This estimation can be done based on either p or q since their sparsity patterns perfectly match. Finally, we threshold the selection probabilities to identify nodes that belong to the same subnetwork. A threshold τ that bounds the expected number of false nodes in a subnetwork, E, is given by [16]:
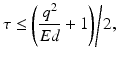
where q is the average number of nodes per subnetwork, which can be estimated as the sum of selection probabilities of all nodes averaged over η. We set E to 1 so that the average number of false nodes included in a subnetwork is statistically controlled to be less than or equal to 1. We declare the set of nodes with selection probabilities higher than the resulting τ for any η to be a subnetwork [16]. We note that each subnetwork identified by CRD is refined independently using the above procedure.
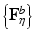 and
and 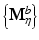 from each bootstrap sample F b and M b . We then apply CRD on each
from each bootstrap sample F b and M b . We then apply CRD on each 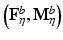 pair. For each η, we estimate the selection probability of each node as the proportion of bootstrap samples in which the given node attains a nonzero weight [16]. This estimation can be done based on either p or q since their sparsity patterns perfectly match. Finally, we threshold the selection probabilities to identify nodes that belong to the same subnetwork. A threshold τ that bounds the expected number of false nodes in a subnetwork, E, is given by [16]:
pair. For each η, we estimate the selection probability of each node as the proportion of bootstrap samples in which the given node attains a nonzero weight [16]. This estimation can be done based on either p or q since their sparsity patterns perfectly match. Finally, we threshold the selection probabilities to identify nodes that belong to the same subnetwork. A threshold τ that bounds the expected number of false nodes in a subnetwork, E, is given by [16]: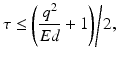
(6)
2.4 Coupled Stable Overlapping Replicator Dynamics
Since CRD is deterministic, reapplying it with the same initialization will converge to the same local maximum. Here, we adopt a graph augmentation strategy that enables destabilization of previously-found local maxima without altering the location of the others [12]. Reapplying CRD on this augmented graph would thus converge to one of the remaining local maxima. The required graph augmentation is as follows [20]:
![$$ {\mathbf{F}}_{ij}^{aug} = \left\{ {\begin{array}{*{20}l} {{\mathbf{F}}_{ij} } \hfill & {{\text{if }}i,j \le d} \hfill \\ \alpha \hfill & {{\text{if }}j > d\;{\text{and}}\;i \notin S_{j – d} } \hfill \\ \beta \hfill & {{\text{if }}i,j > d\;{\text{and}}\;i = j} \hfill \\ {\gamma_{ij} } \hfill & {{\text{if }}i > d\;{\text{and}}\;j \in S_{i – d} } \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right., $$” src=”/wp-content/uploads/2016/09/A339424_1_En_61_Chapter_Equ7.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(7)</DIV></DIV><br />
<DIV id=Equa class=Equation><br />
<DIV class=EquationContent><br />
<DIV class=MediaObject><IMG alt=]() 1, $$” src=”/wp-content/uploads/2016/09/A339424_1_En_61_Chapter_Equa.gif”>
1, $$” src=”/wp-content/uploads/2016/09/A339424_1_En_61_Chapter_Equa.gif”>




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree