Structure of Matter
1.1. THE ATOM
All matter is composed of individual entities called elements. Each element is distinguishable from the others by the physical and chemical properties of its basic component—the atom. Originally thought to be the “smallest” and “indivisible” particle of matter, the atom is now known to have a substructure and can be “divided” into smaller components. Each atom consists of a small central core, the nucleus, where most of the atomic mass is located and a surrounding “cloud” of electrons moving in orbits around the nucleus. Whereas the radius of the atom (radius of the electronic orbits) is approximately 10-10 m, the nucleus has a much smaller radius, namely, about 10-15 m. Thus, for a high-energy electron, photon, or a particle of size comparable to nuclear dimensions, it will be quite possible to penetrate several atoms of matter before a collision happens. As will be pointed out in the chapters ahead, it is important to keep track of those particles or photons that have not interacted with the atoms and those that have suffered collisions.
1.2. THE NUCLEUS
The properties of atoms are derived from the constitution of their nuclei and the number and the organization of the orbital electrons.
The nucleus contains two kinds of fundamental particles: protons and neutrons. Whereas protons are positively charged, neutrons have no charge. Because the electron has a negative unit charge (1.602 × 10-19 C) and the proton has a positive unit charge, the number of protons in the nucleus is equal to the number of electrons outside the nucleus of an electrically neutral atom.
An atom is completely specified by the formula 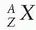 , where X is the chemical symbol for the element; A is the mass number, defined as the number of nucleons (neutrons and protons in the nucleus); and Z is the atomic number, denoting the number of protons in the nucleus (or the number of electrons outside the nucleus). An atom represented in such a manner is also called a nuclide. For example,
, where X is the chemical symbol for the element; A is the mass number, defined as the number of nucleons (neutrons and protons in the nucleus); and Z is the atomic number, denoting the number of protons in the nucleus (or the number of electrons outside the nucleus). An atom represented in such a manner is also called a nuclide. For example,  and
and 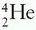 represent atoms or nuclei or nuclides of hydrogen and helium, respectively.
represent atoms or nuclei or nuclides of hydrogen and helium, respectively.
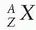 , where X is the chemical symbol for the element; A is the mass number, defined as the number of nucleons (neutrons and protons in the nucleus); and Z is the atomic number, denoting the number of protons in the nucleus (or the number of electrons outside the nucleus). An atom represented in such a manner is also called a nuclide. For example,
, where X is the chemical symbol for the element; A is the mass number, defined as the number of nucleons (neutrons and protons in the nucleus); and Z is the atomic number, denoting the number of protons in the nucleus (or the number of electrons outside the nucleus). An atom represented in such a manner is also called a nuclide. For example,  and
and 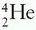 represent atoms or nuclei or nuclides of hydrogen and helium, respectively.
represent atoms or nuclei or nuclides of hydrogen and helium, respectively.On the basis of different proportions of neutrons and protons in the nuclei, atoms have been classified into the following categories: isotopes, atoms having nuclei with the same number of protons but different number of neutrons; isotones, atoms having the same number of neutrons but different number of protons; isobars, atoms with the same number of nucleons but different number of protons; and isomers, atoms containing the same number of protons as well as neutrons. The last category, namely isomers, represents identical atoms except that they differ in their nuclear energy states. For example, 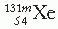 (m stands for metastable state) is an isomer of
(m stands for metastable state) is an isomer of 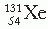 .
.
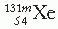 (m stands for metastable state) is an isomer of
(m stands for metastable state) is an isomer of 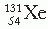 .
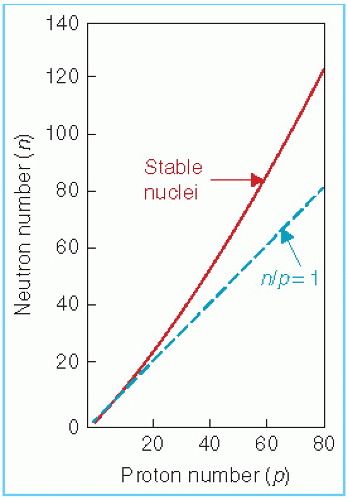
.Certain combinations of neutrons and protons result in stable (nonradioactive) nuclides than others. For instance, stable elements in the low atomic number range have an almost equal number of neutrons, N, and protons, Z. However, as Z increases beyond about 20, the neutron-to-proton ratio for stable nuclei becomes greater than 1 and increases with Z. This is evident in Figure 1.1, which shows a plot of the number of neutrons versus protons in stable nuclei.
Nuclear stability has also been analyzed in terms of even and odd numbers of neutrons and protons. Of about 300 different stable isotopes, more than half have even numbers of protons and neutrons and are known as even-even nuclei. This suggests that nuclei gain stability when neutrons and protons are mutually paired. On the other hand, only four stable nuclei exist that have both odd Z and odd N, namely 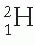 ,
, 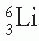 ,
, 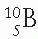 , and
, and 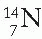 . About 20% of the stable nuclei have even Z and odd N and about the same proportion have odd Z and even N.
. About 20% of the stable nuclei have even Z and odd N and about the same proportion have odd Z and even N.
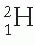 ,
, 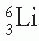 ,
, 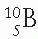 , and
, and 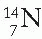 . About 20% of the stable nuclei have even Z and odd N and about the same proportion have odd Z and even N.
. About 20% of the stable nuclei have even Z and odd N and about the same proportion have odd Z and even N.1.3. ATOMIC MASS AND ENERGY UNITS
Masses of atoms and atomic particles are conveniently given in terms of atomic mass unit (amu). An amu is defined as 1/12 of the mass of a 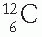 atom. Thus, the
atom. Thus, the 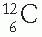 atom is arbitrarily assigned the mass equal to 12 amu. In basic units of mass,
atom is arbitrarily assigned the mass equal to 12 amu. In basic units of mass,
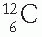 atom. Thus, the
atom. Thus, the 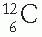 atom is arbitrarily assigned the mass equal to 12 amu. In basic units of mass,
atom is arbitrarily assigned the mass equal to 12 amu. In basic units of mass,1 amu = 1.66 × 10−27 kg
The mass of an atom expressed in terms of amu is known as atomic mass or atomic weight. Another useful term is gram atomic weight, which is defined as the mass in grams numerically equal to the atomic weight. According to Avogadro’s law, every gram atomic weight of a substance contains the same number of atoms. The number, referred to as Avogadro number or Avogadro constant (NA), has been measured by many investigators, and its currently accepted value is 6.0221 × 1023 atoms per gram atomic weight (or mole).
From the previous definitions, one can calculate other quantities of interest such as the number of atoms per gram, grams per atom, and electrons per gram. Considering helium as an example, its atomic weight (AW) is equal to 4.0026.
Therefore,
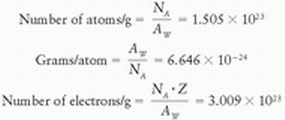
The masses of atomic particles, according to the amu, are electron = 0.000548 amu, proton = 1.00727 amu, and neutron = 1.00866 amu.
Because the mass of an electron is much smaller than that of a proton or neutron and protons and neutrons have nearly the same mass, equal to approximately 1 amu, all the atomic masses in units of amu are very nearly equal to the mass number. However, it is important to point out that the mass of an atom is not exactly equal to the sum of the masses of constituent particles.
The reason for this is that, when the nucleus is formed, a certain mass is destroyed and converted into energy that acts as a “glue” to keep the nucleons together. This mass difference is called the mass defect. Looking at it from a different perspective, an amount of energy equal to the mass defect must be supplied to separate the nucleus into individual nucleons. Therefore, this energy is also called the binding energy of the nucleus.
The reason for this is that, when the nucleus is formed, a certain mass is destroyed and converted into energy that acts as a “glue” to keep the nucleons together. This mass difference is called the mass defect. Looking at it from a different perspective, an amount of energy equal to the mass defect must be supplied to separate the nucleus into individual nucleons. Therefore, this energy is also called the binding energy of the nucleus.
The basic unit of energy is joule (J) and is equal to the work done when a force of 1 newton acts through a distance of 1 m. The newton, in turn, is a unit of force given by the product of mass (1 kg) and acceleration (1 m/s2). However, a more convenient energy unit in atomic and nuclear physics is electron volt (eV), defined as the kinetic energy acquired by an electron in passing through a potential difference of 1 V. It can be shown that the work done in this case is given by the product of potential difference and the charge on the electron. Therefore, we have
1 eV = 1 V × 1.602 × 10-19 C = 1.602 × 10-19 J
Multiples of this unit are
keV = 1,000 eV
3c1 million eV (MeV) = 1,000,000 eV
According to Einstein’s principle of equivalence of mass and energy, a mass m is equivalent to energy E and the relationship is given by
where c is the velocity of light (3 × 108 m/s). For example, a mass of 1 kg, if converted to energy, is equivalent to
E = 1 kg × (3 × 108 m/s)2 = 9 × 1016 J = 5.62 × 1029 MeV
The mass of an electron at rest is sometimes expressed in terms of its energy equivalent (E0). Because its mass is 9.1 × 10-31 kg, we have from Equation 1.1:
E0 = 0.511 MeV
Another useful conversion is that of amu to energy. It can be shown that
1 amu = 931.5 MeV
From Equation 1.1, we can see that the equivalent mass of any particle of total energy E (kinetic plus rest mass energy) is given by E/c2. Accordingly, masses of particles may also be expressed in units of GeV/c2. It can be shown that
1 GeV/c2 = 1.0723 amu
In the above examples, we have not considered the effect of particle velocity on its mass. Experiments with high-speed particles have shown that the mass of a particle depends on its velocity and that it increases with velocity. The relationship between mass and velocity can be derived from Einstein’s theory of relativity. If m is the mass of a particle moving with velocity υ and m0 is its rest mass, then

The kinetic energy (Ek) is given by

It should be noted that the relativistic effect of velocity on mass becomes important when a particle travels with a velocity comparable to that of light.
1.4. DISTRIBUTION OF ORBITAL ELECTRONS
According to the model proposed by Niels Bohr in 1913, the electrons revolve around the nucleus in specific orbits and are prevented from leaving the atom by the centripetal force of attraction between the positively charged nucleus and the negatively charged electron.
On the basis of classical physics, an accelerating or revolving electron must radiate energy. This would result in a continuous decrease of the radius of the orbit with the electron eventually spiraling into the nucleus. However, the data on the emission or absorption of radiation by
elements reveal that the change of energy is not continuous but discrete. To explain the observed line spectrum of hydrogen, Bohr theorized that the sharp lines of the spectrum represented electron jumps from one orbit down to another with the emission of light of a particular frequency or a quantum of energy. He proposed two fundamental postulates: (a) electrons can exist only in those orbits for which the angular momentum of the electron is an integral multiple of h/2π, where h is the Planck’s constant (6.626 × 10-34 J-sec); and (b) no energy is gained or lost while the electron remains in any one of the permissible orbits.
elements reveal that the change of energy is not continuous but discrete. To explain the observed line spectrum of hydrogen, Bohr theorized that the sharp lines of the spectrum represented electron jumps from one orbit down to another with the emission of light of a particular frequency or a quantum of energy. He proposed two fundamental postulates: (a) electrons can exist only in those orbits for which the angular momentum of the electron is an integral multiple of h/2π, where h is the Planck’s constant (6.626 × 10-34 J-sec); and (b) no energy is gained or lost while the electron remains in any one of the permissible orbits.
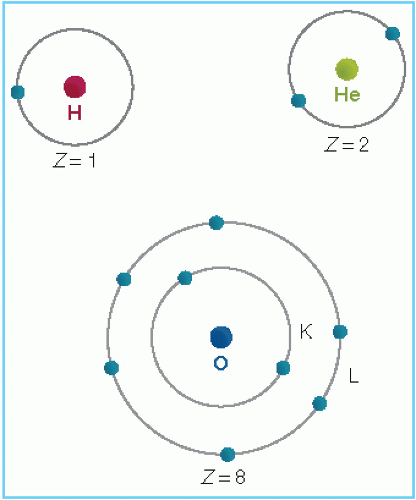
The arrangement of electrons outside the nucleus is governed by the rules of quantum mechanics and the Pauli exclusion principle (not discussed here). Although the actual configuration of electrons is rather complex and dynamic, one may simplify the concept by assigning electrons to specific orbits. The innermost orbit or shell is called the K shell. The next shells are L, M, N, and O. The maximum number of electrons in an orbit is given by 2n2, where n is the orbit number. For example, a maximum of 2 electrons can exist in the first orbit, 8 in the second, and 18 in the third. Figure 1.2 shows the electron orbits of hydrogen, helium, and oxygen atoms.
A shell need not be completely filled before the electrons begin to fill the next shell.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree