1,500 ms, echo time (TE)  147 ms, flip angle
147 ms, flip angle  150 and number of averages
150 and number of averages 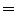 2, having a resolution of
2, having a resolution of 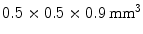 have been utilized for testing and validating the segmentation approach.
have been utilized for testing and validating the segmentation approach.
Five herniated discs has been manually segmented under expert [12] supervision to be used for quantitative evaluation of the proposed semi-supervised automatic segmentation framework, with results discussed in the Sect. 4.
3.2 Image Preprocessing
An anisotropic diffusion [13] filter (conductance 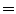 0.8, timestep
0.8, timestep 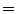 0.5, iterations
0.5, iterations 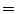 50) has been applied to the volumetric images to reduce image noise within the structures while preserving image boundaries. The filter mitigates image intensity inhomogeneity located around the disc due to overlapping image intensities of the herniated disc boundary and the surrounding posterior ligament [14]. The Insight Segmentation and Registration Toolkit (ITK) [15] has been utilized for applying image preprocessing filters.
50) has been applied to the volumetric images to reduce image noise within the structures while preserving image boundaries. The filter mitigates image intensity inhomogeneity located around the disc due to overlapping image intensities of the herniated disc boundary and the surrounding posterior ligament [14]. The Insight Segmentation and Registration Toolkit (ITK) [15] has been utilized for applying image preprocessing filters.
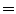 0.8, timestep
0.8, timestep 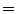 0.5, iterations
0.5, iterations 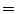 50) has been applied to the volumetric images to reduce image noise within the structures while preserving image boundaries. The filter mitigates image intensity inhomogeneity located around the disc due to overlapping image intensities of the herniated disc boundary and the surrounding posterior ligament [14]. The Insight Segmentation and Registration Toolkit (ITK) [15] has been utilized for applying image preprocessing filters.
50) has been applied to the volumetric images to reduce image noise within the structures while preserving image boundaries. The filter mitigates image intensity inhomogeneity located around the disc due to overlapping image intensities of the herniated disc boundary and the surrounding posterior ligament [14]. The Insight Segmentation and Registration Toolkit (ITK) [15] has been utilized for applying image preprocessing filters.3.3 Model Initialization Through Landmark-Based Affine Registration
An ellipsoidal template mesh is initialized within the herniated disc image volume for simplex mesh deformation. Arbitrary translation, rotation and scaling effects need to be captured between the template mesh and MRI image. Six landmarks are manually placed on the ellipsoidal template mesh corresponding to landmarks within the herniated disc image boundary to initialize the template within the herniated disc image through affine registration. These landmarks are placed at the center, as well as the superior, inferior, anterior and posterior points of the disc, as well as one at the center of the superior disc surface to characterize rotation. The initialized template mesh is then allowed to automatically deform using a multi-resolution surface model, as described in Sect. 3.4.
3.4 Automatic Multi-resolution Simplex Deformation
This research exploits simplex mesh discrete deformable models for segmentation of intervertebral discs. Introduced by Delingette [16] for 3D shape reconstruction and segmentation, a 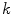 -simplex mesh is a
-simplex mesh is a 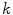 -manifold discrete mesh with exactly
-manifold discrete mesh with exactly 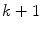 distinct neighbors [27]. A simplex mesh has the property of constant vertex connectivity. Simplex meshes can represent various objects depending on the connectivity
distinct neighbors [27]. A simplex mesh has the property of constant vertex connectivity. Simplex meshes can represent various objects depending on the connectivity 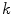 , where 1-simplex represents a curve, a 2-simplex represents a surface, and a 3-simplex represents a volume. Our research is focused on surface representation for image segmentation using 2-simplex meshes with constant 3-vertex connectivity.
, where 1-simplex represents a curve, a 2-simplex represents a surface, and a 3-simplex represents a volume. Our research is focused on surface representation for image segmentation using 2-simplex meshes with constant 3-vertex connectivity.
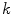 -simplex mesh is a
-simplex mesh is a 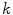 -manifold discrete mesh with exactly
-manifold discrete mesh with exactly 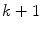 distinct neighbors [27]. A simplex mesh has the property of constant vertex connectivity. Simplex meshes can represent various objects depending on the connectivity
distinct neighbors [27]. A simplex mesh has the property of constant vertex connectivity. Simplex meshes can represent various objects depending on the connectivity 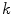 , where 1-simplex represents a curve, a 2-simplex represents a surface, and a 3-simplex represents a volume. Our research is focused on surface representation for image segmentation using 2-simplex meshes with constant 3-vertex connectivity.
, where 1-simplex represents a curve, a 2-simplex represents a surface, and a 3-simplex represents a volume. Our research is focused on surface representation for image segmentation using 2-simplex meshes with constant 3-vertex connectivity.The constant connectivity of the 2-simplex mesh leads to three simplex parameters corresponding to a vertex with a mass and its three neighboring vertices that are invariant under similarity transformations [16]. These independent simplex parameters can be utilized to represent the geometric constraints enforced upon a vertex with respect to its three neighbor vertices. The dynamics of each vertex 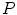 are governed by a Newtonian law of motion represented by the equation
are governed by a Newtonian law of motion represented by the equation
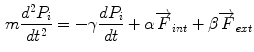
where 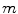 is the vertex mass,
is the vertex mass, 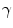 is the damping force and
is the damping force and 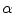 and
and 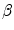 are the weight factors of the internal and external forces respectively.
are the weight factors of the internal and external forces respectively. 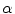 has an average value of
has an average value of 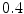 and
and 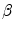 has an average value of
has an average value of 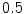 in our approach. Appropriate values of
in our approach. Appropriate values of 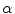 and
and 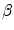 are selected prior to segmentation and are consistent across a dataset.
are selected prior to segmentation and are consistent across a dataset. 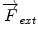 is the sum of external forces governed by image edge information and gradient intensity values that minimize the distance between a vertex
is the sum of external forces governed by image edge information and gradient intensity values that minimize the distance between a vertex 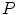 and maximum gradient intensity in the neighborhood of
and maximum gradient intensity in the neighborhood of 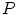 along the normal direction.
along the normal direction. 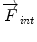 is the sum of internal forces represented by an elastic force that enforces smoothness and weak shape-based constraints. This physically-based deformable model is governed by forces to maintain internal stabilization through
is the sum of internal forces represented by an elastic force that enforces smoothness and weak shape-based constraints. This physically-based deformable model is governed by forces to maintain internal stabilization through 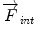 . Weak shape memory is enforced by constraining the internal forces along the normal direction of vertex
. Weak shape memory is enforced by constraining the internal forces along the normal direction of vertex 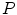 . This is implemented by constraining the mean curvature at vertex
. This is implemented by constraining the mean curvature at vertex 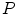 governed by the simplex angle
governed by the simplex angle 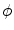 by setting
by setting 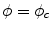 , where
, where 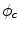 is a constant [16].
is a constant [16].
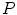 are governed by a Newtonian law of motion represented by the equation
are governed by a Newtonian law of motion represented by the equation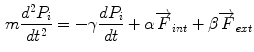
(1)
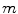 is the vertex mass,
is the vertex mass, 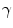 is the damping force and
is the damping force and 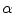 and
and 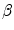 are the weight factors of the internal and external forces respectively.
are the weight factors of the internal and external forces respectively. 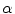 has an average value of
has an average value of 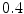 and
and 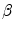 has an average value of
has an average value of 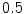 in our approach. Appropriate values of
in our approach. Appropriate values of 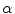 and
and 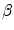 are selected prior to segmentation and are consistent across a dataset.
are selected prior to segmentation and are consistent across a dataset. 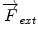 is the sum of external forces governed by image edge information and gradient intensity values that minimize the distance between a vertex
is the sum of external forces governed by image edge information and gradient intensity values that minimize the distance between a vertex 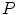 and maximum gradient intensity in the neighborhood of
and maximum gradient intensity in the neighborhood of 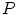 along the normal direction.
along the normal direction. 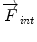 is the sum of internal forces represented by an elastic force that enforces smoothness and weak shape-based constraints. This physically-based deformable model is governed by forces to maintain internal stabilization through
is the sum of internal forces represented by an elastic force that enforces smoothness and weak shape-based constraints. This physically-based deformable model is governed by forces to maintain internal stabilization through 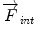 . Weak shape memory is enforced by constraining the internal forces along the normal direction of vertex
. Weak shape memory is enforced by constraining the internal forces along the normal direction of vertex 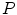 . This is implemented by constraining the mean curvature at vertex
. This is implemented by constraining the mean curvature at vertex 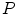 governed by the simplex angle
governed by the simplex angle 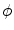 by setting
by setting 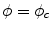 , where
, where 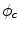 is a constant [16].
is a constant [16].3.5 Multi-resolution Simplex Model Creation
Delingette [16] proposed four topological operators for transformation of a k-simplex mesh, which were refined by Gilles et al. [17] to optimize the simplex mesh quality by applying quality constraints. These operators yield regular mesh faces with desired edge length, leading to high quality multi-resolution meshes.
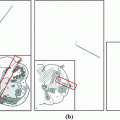
The global mesh resolution is adapted to the complexity of the anatomical shape being segmented in a coarse-to-fine segmentation approach. Thus, various simplex mesh resolutions of a disc and toroidal shape have been generated through a multi-resolution scheme without loss of vertex connectivity for segmentation refinement, as demonstrated in Fig. 1.


Fig. 1
Multi-resolution segmentation refinement herniated disc model
Template mesh deformation is guided by the presence of MR image gradient forces, resulting in 3–6 min of segmentation time per disc or vertebra. The resulting simplex mesh is converted to a dual triangulated surface mesh with resolution control, which in turn is directly input to a tetrahedralization of similar resolution for simulation, as discussed in Sect. 3.7.
3.6 User-Guided Pathology Segmentation
In the event that the internal simplex shape memory influence hinders detection of pathology, as detected via visual inspection, user input is allowed to locally turn off the shape feature and assist model deformation. This assistance is implemented by placing 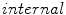 and
and 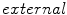 constraint points on the volumetric image that gracefully constrain the deformation to correct under-and over-segmentation. Constraint point forces are enforced as an addition to the total external force. The number of constraint points applied to the images typically range between 37 and 60, while requiring 5–7 min, depending on the shape of the pathology that the automatic Simplex model deformation may fail to capture.
constraint points on the volumetric image that gracefully constrain the deformation to correct under-and over-segmentation. Constraint point forces are enforced as an addition to the total external force. The number of constraint points applied to the images typically range between 37 and 60, while requiring 5–7 min, depending on the shape of the pathology that the automatic Simplex model deformation may fail to capture.
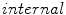 and
and 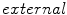 constraint points on the volumetric image that gracefully constrain the deformation to correct under-and over-segmentation. Constraint point forces are enforced as an addition to the total external force. The number of constraint points applied to the images typically range between 37 and 60, while requiring 5–7 min, depending on the shape of the pathology that the automatic Simplex model deformation may fail to capture.
constraint points on the volumetric image that gracefully constrain the deformation to correct under-and over-segmentation. Constraint point forces are enforced as an addition to the total external force. The number of constraint points applied to the images typically range between 37 and 60, while requiring 5–7 min, depending on the shape of the pathology that the automatic Simplex model deformation may fail to capture.This semi-supervised segmentation method has also been utilized for manual correction of healthy intervertebral disc segmentation, which serves as ground truth for validation of our healthy disc segmentation results. Similar segmentation evaluation techniques have been employed in literature using manually corrected active shape models for segmentation of anatomical structures [8, 18]. Manual segmentation is a labor intensive process; each MRI volume consists of about 85–90 image slices in the sagittal plane, with an average segmentation time of approximately 7 h of manual segmentation time per disc. An anatomist performed manual and semi-supervised segmentation for generation of ground truth verified by a neuroradiologist.
3.7 Intervertebral Disc Simulation Model
Simulation Open Framework Architecture (SOFA) [19] is an open-source object-oriented software toolkit that is targeted towards real-time interactive medical simulations. Several components of a model can be combined in hierarchies through an easy-to-use scene file format to represent various model parameters such as material properties, deformable behavior, constraints and boundary conditions, which makes SOFA a very powerful and efficient prototyping tool. The following section describes two SOFA applications using the disc surface mesh: a deformation based on an FEM model and cutting based on an enriched Meshless Mechanics (MM)-based model.
3.7.1 Healthy Disc Compression Simulation
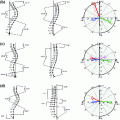
A healthy lumbar intervertebral disc has been modeled using SOFA to simulate the biomechanical and physiological changes of the disc under compression [19]. The tetrahedral mesh of the healthy L2–L3 disc has been generated from the segmented surface mesh using the isosurface stuffing method [20]. This volumetric mesh has been used to define the tetrahedral corotational finite element model of the disc, depicted in Fig. 2a, which corresponds to the Behavior Model 1 of the deformable object. The boundary conditions and external compression forces have been defined through the segmented surface mesh, which is linked to the underlying Behavior Model of the deformable object (Fig. 2b). Following the actual anatomy of the simulated intervertebral disc, the bottom nodes that are in direct contact with the below rigid vertebral body have been constrained to be fixed to their initial locations, and a prescribed vertical pressure of 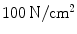 has been applied to the top surface of the disc using SOFA’s TrianglePressureForceField2 component.
has been applied to the top surface of the disc using SOFA’s TrianglePressureForceField2 component.

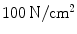 has been applied to the top surface of the disc using SOFA’s TrianglePressureForceField2 component.
has been applied to the top surface of the disc using SOFA’s TrianglePressureForceField2 component.
Fig. 2




3D simulation of a healthy intervertebral disc under pressure. a Tetrahedral FEM. b Behavioral Model: The bottom nodes (red) are constrained to be fixed and the Neumann boundary condition is applied to the top surface (green) of the disc model. c Visual Model: Comparison of the disc model at rest (red) and deformed (green) configurations (Color figure online)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree