1.
Color based segmentation: Color is an effective cue in computer vision for identifying regions of interest/objects in the image. For example, skin color segmentation is one of the most widely used techniques in various vision applications due to the perceptual importance of skin color in human visual system. Most of existing skin color segmentation methods are derived from an assumption that the skin colors of different subjects form a small cluster in colorspace provided that the images are captured under controlled lighting setup [46]. In real-world scene, where illumination condition varies substantially depending on the prevailing illuminant, color constancy algorithm can be applied prior to executing segmentation solution to maintain stable performance [48].
2.
Face recognition: Since faces play a crucial role in human social interaction, facial analysis is one of the most active areas of research in digital imaging. A key challenge in automatic face recognition technology lies in achieving high identification accuracy under uncontrolled imaging conditions. To this end, extraction of highly discriminative features which are invariant to illumination and sensor characteristic can significantly improve the machine recognition of faces [2].
3.
Novel consumer imaging devices: With the rapid advancement of the consumer electronics, customers have higher requirements for the quality of the products. In digital photography, the visual quality of the captured image is a key criterion to judge the performance of the digital cameras. Many digital cameras provide the auto white balance (AWB) functionality, which helps less-experienced users to take a high quality photo under an unknown illumination condition that has the same chromatic representation as the ones taken under sunlight.
2 Color Image Formation in Digital Imaging Devices
2.1 Physical Reflection Model
There are three main factors that are closely related in the process of color image generation in imaging devices: (i) the underlying physical properties of the imaged surfaces (object), (ii) the nature of the light source incident upon those surfaces, (iii) the characteristics of the imaging system. A fundamental question related to stable color representation in digital image data is “how to derive the process of color image formulation in image acquisition devices using the physical laws of light?”. Especially we are interested in color images recorded in RGB system due to its dominant usage in digital imaging technology. Shafer has created a simple physical model of the reflection process, called the dichromatic reflection model (DRM) [61], to capture an important relationship between light sources, surface reflectances, and imaging devices. This model has become the foundation of various color constancy and color invariance methods.
According to the DRM, inhomogeneous dielectric material2 consists of a clear substrate with embedded colorant particles. The model states that the light reflected from an object is caused by two types of reflections.
Thus, reflection of inhomogeneous objects can be modeled as a linear combination of diffuse and specular reflections (Fig. 2):
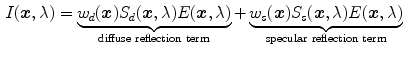
where 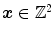 is the two-dimensional spatial position of a surface point, and
is the two-dimensional spatial position of a surface point, and 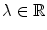 is wavelength,
is wavelength, 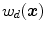 and
and 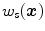 are the geometrical parameters for diffuse and specular reflection, respectively, whose values are depending on the geometric structure at location
are the geometrical parameters for diffuse and specular reflection, respectively, whose values are depending on the geometric structure at location 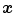 (e.g. the viewing angle, light source direction, and surface orientation).
(e.g. the viewing angle, light source direction, and surface orientation). 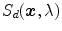 is the diffuse spectral reflectance function,
is the diffuse spectral reflectance function, 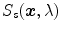 is the specular spectral reflectance function, and
is the specular spectral reflectance function, and 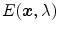 is the spectral power distribution (SPD) function of the illumination. According to well-known Neutral Interface Reflection (NIR) assumption, for many dielectric inhomogeneous objects the index of refraction does not change significantly over the visible spectrum, thus it can be assume to be constant (i.e.
is the spectral power distribution (SPD) function of the illumination. According to well-known Neutral Interface Reflection (NIR) assumption, for many dielectric inhomogeneous objects the index of refraction does not change significantly over the visible spectrum, thus it can be assume to be constant (i.e. 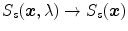 ) [51]. As a result, (1) becomes:
) [51]. As a result, (1) becomes:
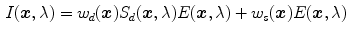
where 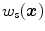 now contains both the geometry dependent parameter and the constant reflectance of specular term.
now contains both the geometry dependent parameter and the constant reflectance of specular term.
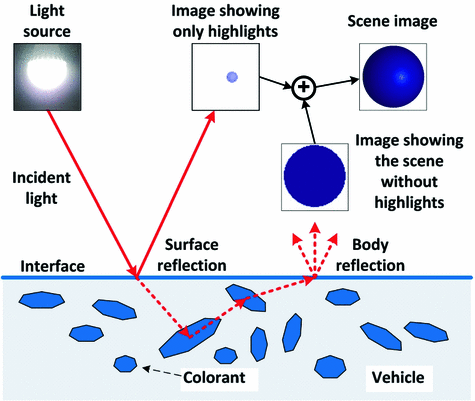
Body (diffuse) reflection: The incident light enters the object surface where it is selectively absorbed and emitted by colorant particles within the material body. Afterwards, the light is reflected back into the air through the surface. Diffuse component of the incident light is spectrally altered depending on properties of the surface. The body reflection component is almost random in its direction.
Surface (specular) reflection: The surface of an object acts like a mirror by simply reflecting any light which is incident upon it. For many inhomogeneous materials, specular component of the reflected light is spectrally similar to the incident light, as the light does not interact with the surface. Generally, surface reflection component is more directional than body component.
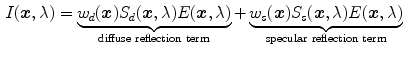
(1)
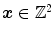 is the two-dimensional spatial position of a surface point, and
is the two-dimensional spatial position of a surface point, and 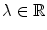 is wavelength,
is wavelength, 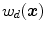 and
and 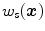 are the geometrical parameters for diffuse and specular reflection, respectively, whose values are depending on the geometric structure at location
are the geometrical parameters for diffuse and specular reflection, respectively, whose values are depending on the geometric structure at location 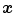 (e.g. the viewing angle, light source direction, and surface orientation).
(e.g. the viewing angle, light source direction, and surface orientation). 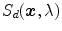 is the diffuse spectral reflectance function,
is the diffuse spectral reflectance function, 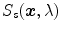 is the specular spectral reflectance function, and
is the specular spectral reflectance function, and 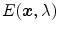 is the spectral power distribution (SPD) function of the illumination. According to well-known Neutral Interface Reflection (NIR) assumption, for many dielectric inhomogeneous objects the index of refraction does not change significantly over the visible spectrum, thus it can be assume to be constant (i.e.
is the spectral power distribution (SPD) function of the illumination. According to well-known Neutral Interface Reflection (NIR) assumption, for many dielectric inhomogeneous objects the index of refraction does not change significantly over the visible spectrum, thus it can be assume to be constant (i.e. 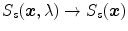 ) [51]. As a result, (1) becomes:
) [51]. As a result, (1) becomes: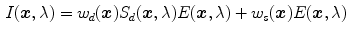
(2)
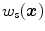 now contains both the geometry dependent parameter and the constant reflectance of specular term.
now contains both the geometry dependent parameter and the constant reflectance of specular term.
Fig. 2
The dichromatic reflection model of inhomogeneous dielectric material
In (2), light reflections are described using continuous spectra. However, digital cameras typically use 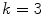 samples to describe the light spectrum. Sample measurements are obtained by filtering the input light spectrum and integrating over filtered spectrum. According to the DRM, an image taken by a digital color camera can be expressed as:
samples to describe the light spectrum. Sample measurements are obtained by filtering the input light spectrum and integrating over filtered spectrum. According to the DRM, an image taken by a digital color camera can be expressed as:
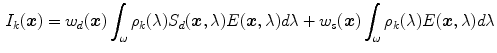
where 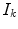 is the sensor response (RGB pixel values) of
is the sensor response (RGB pixel values) of 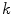 color channel (
color channel (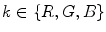 ), and
), and 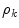 is the sensor spectral sensitivity of
is the sensor spectral sensitivity of 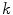 color channel. The integration is done over the visible spectrum
color channel. The integration is done over the visible spectrum 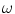 . It should be noted that camera noise and gain are ignored in this formulation for simplicity.
. It should be noted that camera noise and gain are ignored in this formulation for simplicity.
 samples to describe the light spectrum. Sample measurements are obtained by filtering the input light spectrum and integrating over filtered spectrum. According to the DRM, an image taken by a digital color camera can be expressed as:
samples to describe the light spectrum. Sample measurements are obtained by filtering the input light spectrum and integrating over filtered spectrum. According to the DRM, an image taken by a digital color camera can be expressed as: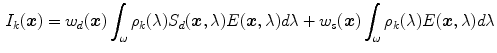
(3)
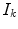 is the sensor response (RGB pixel values) of
is the sensor response (RGB pixel values) of 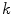 color channel (
color channel (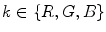 ), and
), and 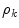 is the sensor spectral sensitivity of
is the sensor spectral sensitivity of 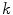 color channel. The integration is done over the visible spectrum
color channel. The integration is done over the visible spectrum 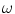 . It should be noted that camera noise and gain are ignored in this formulation for simplicity.
. It should be noted that camera noise and gain are ignored in this formulation for simplicity.To simplify the problem, many researchers [12, 25, 49, 69] have considered a simplified scene in which all objects are flat, matte, Lambertian surfaces.3 In this simplified imaging condition, the specular reflection term in (3) can be discarded and the Lambertian reflection model is obtained as follows:
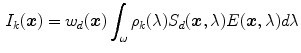
Note that for many materials the Lambertian model does not hold in the strict sense. For example, materials with glossy surfaces often cause specularities at some spots on the material where omission of specular reflection term can be problematic. However, the Lambertian model is a good approximation since often the specularities only occupy a small part of the objects, and therefore, widely used in design of tractable color constancy and invariance solutions.
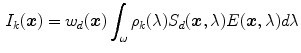
(4)
2.2 Linear and Non-linear RGB Representation
In the research of stable color representation, it is important to discriminate between linear and non-linear RGB representation, since unacceptable results may be obtained when they are used without caution. Linear RGB values are proportional to the intensity of the physical power radiated from an object around 700, 550, and 440 nm bands of the visible spectrum, respectively. Thus, RGB responses estimated by (4) is considered as the linear RGB. In practical image acquisition systems (e.g. digital cameras), the device RGB responses are often not linearly related to the values suggested by (4), but rather they are transformed to non-linear RGB signals through the gamma correction. Several gamma correction functions exist depending on applications, and the one that mostly related to our discussion is defined in International Electrotechinical Commission (IEC) sRGB gamma transfer function (gamma correction used in most cameras, PCs, and printers):
![$$\begin{aligned} I_k^{\prime } = {\left\{ \begin{array}{ll} 12.92I_k, &{} \mathrm{if }\, I_k \le 0.0031308 \\ 1.055I_k^{1/2.4} - 0.055, &{} \mathrm{otherwise } \end{array}\right. }, (I_k \in [0,1]) \end{aligned}$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_Equ5.gif)
where 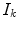 is the intensity of linear RGB,
is the intensity of linear RGB, 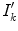 is the intensity of nonlinear RGB (
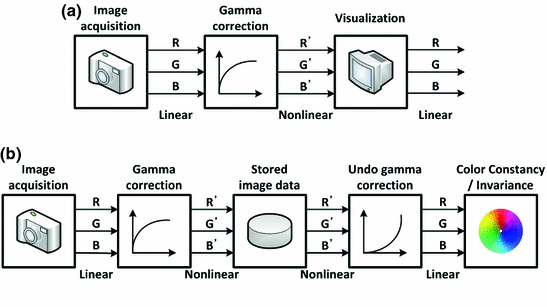
is the intensity of nonlinear RGB (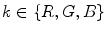 ). It is worthwhile to note that even though the sRGB standard uses a power function with an exponent of 2.4, the transfer curve is better represented as a power function with an exponent of 2.2 [56]. The gamma correction is applied to correct a nonlinear characteristic of the cathode ray tube (CRT) display devices. The CRT display is nonlinear in a sense that the intensity of light reproduced at the screen is a nonlinear function of the input voltage. Thus, compensation for this nonlinearity is a main objective of the gamma correction process. For color images, the linear RGB values are converted into nonlinear voltages R’ G’ B’ through the gamma correction and the CRT monitor will then convert corrected R’ G’ B’ values into linear RGB values to reproduce the original color (See Fig. 3a). The transformation from gamma corrected R’ G’ B’ to linear RGB values can be formulated as:
). It is worthwhile to note that even though the sRGB standard uses a power function with an exponent of 2.4, the transfer curve is better represented as a power function with an exponent of 2.2 [56]. The gamma correction is applied to correct a nonlinear characteristic of the cathode ray tube (CRT) display devices. The CRT display is nonlinear in a sense that the intensity of light reproduced at the screen is a nonlinear function of the input voltage. Thus, compensation for this nonlinearity is a main objective of the gamma correction process. For color images, the linear RGB values are converted into nonlinear voltages R’ G’ B’ through the gamma correction and the CRT monitor will then convert corrected R’ G’ B’ values into linear RGB values to reproduce the original color (See Fig. 3a). The transformation from gamma corrected R’ G’ B’ to linear RGB values can be formulated as:
![$$\begin{aligned} I_k = {\left\{ \begin{array}{ll} \dfrac{I_k^{\prime }}{12.92}, &{} \mathrm{if }\, I_k^{\prime } \le 0.03928 \\ \left( \dfrac{I_k^{\prime }+0.055}{1.055}\right) ^{2.4}, &{} \mathrm{otherwise } \end{array}\right. } ,(I_k^{\prime } \in [0,1]) \end{aligned}$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_Equ6.gif)
Computer images are often stored with a gamma corrected value (e.g. stored images in JPG or TIFF file format). When we process stored nonlinear image signal, we need to linearize the intensity values by undoing gamma correction, since underlying physical reflectance models (e.g. (3) and (4)) for color constancy/invariance algorithms are derived using linear RGB values (See Fig. 3b).
![$$\begin{aligned} I_k^{\prime } = {\left\{ \begin{array}{ll} 12.92I_k, &{} \mathrm{if }\, I_k \le 0.0031308 \\ 1.055I_k^{1/2.4} - 0.055, &{} \mathrm{otherwise } \end{array}\right. }, (I_k \in [0,1]) \end{aligned}$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_Equ5.gif)
(5)
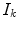 is the intensity of linear RGB,
is the intensity of linear RGB, 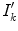 is the intensity of nonlinear RGB (
is the intensity of nonlinear RGB (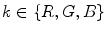 ). It is worthwhile to note that even though the sRGB standard uses a power function with an exponent of 2.4, the transfer curve is better represented as a power function with an exponent of 2.2 [56]. The gamma correction is applied to correct a nonlinear characteristic of the cathode ray tube (CRT) display devices. The CRT display is nonlinear in a sense that the intensity of light reproduced at the screen is a nonlinear function of the input voltage. Thus, compensation for this nonlinearity is a main objective of the gamma correction process. For color images, the linear RGB values are converted into nonlinear voltages R’ G’ B’ through the gamma correction and the CRT monitor will then convert corrected R’ G’ B’ values into linear RGB values to reproduce the original color (See Fig. 3a). The transformation from gamma corrected R’ G’ B’ to linear RGB values can be formulated as:
). It is worthwhile to note that even though the sRGB standard uses a power function with an exponent of 2.4, the transfer curve is better represented as a power function with an exponent of 2.2 [56]. The gamma correction is applied to correct a nonlinear characteristic of the cathode ray tube (CRT) display devices. The CRT display is nonlinear in a sense that the intensity of light reproduced at the screen is a nonlinear function of the input voltage. Thus, compensation for this nonlinearity is a main objective of the gamma correction process. For color images, the linear RGB values are converted into nonlinear voltages R’ G’ B’ through the gamma correction and the CRT monitor will then convert corrected R’ G’ B’ values into linear RGB values to reproduce the original color (See Fig. 3a). The transformation from gamma corrected R’ G’ B’ to linear RGB values can be formulated as:![$$\begin{aligned} I_k = {\left\{ \begin{array}{ll} \dfrac{I_k^{\prime }}{12.92}, &{} \mathrm{if }\, I_k^{\prime } \le 0.03928 \\ \left( \dfrac{I_k^{\prime }+0.055}{1.055}\right) ^{2.4}, &{} \mathrm{otherwise } \end{array}\right. } ,(I_k^{\prime } \in [0,1]) \end{aligned}$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_Equ6.gif)
(6)

Fig. 3
Color image processing pipeline in general digital imaging devices. a General display pipeline. b General color processing pipeline
3 Color Constancy
3.1 General Formulation of Color Constancy
Essentially, the color constancy problem can be posed as estimating SPD of the scene illuminant 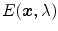 from a given image, and then use this knowledge to recover an image which is independent of the scene illuminant. It is often unnecessary to recover the full spectra of illuminant, rather it is sufficient to represent it by the projection of
from a given image, and then use this knowledge to recover an image which is independent of the scene illuminant. It is often unnecessary to recover the full spectra of illuminant, rather it is sufficient to represent it by the projection of 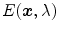 on RGB domain, i.e.
on RGB domain, i.e. ![$$\varvec{e}(\varvec{x}) = [e_R(\varvec{x}), e_G(\varvec{x}), e_B(\varvec{x})]^T$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_IEq28.gif) , where:
, where:
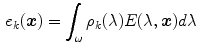
Without prior knowledge, the estimation of 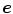 is an under-constrained problem. In practice, color constancy algorithms rely on various assumptions on statistical properties of the illuminant, and surface reflectance properties to estimate
is an under-constrained problem. In practice, color constancy algorithms rely on various assumptions on statistical properties of the illuminant, and surface reflectance properties to estimate 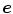 . One of the widely used assumptions is that the scene illumination is constant over the entire image and thus
. One of the widely used assumptions is that the scene illumination is constant over the entire image and thus 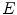 is simply a function of wavelength
is simply a function of wavelength 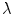 (i.e.
(i.e. 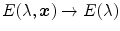 ).
).
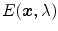 from a given image, and then use this knowledge to recover an image which is independent of the scene illuminant. It is often unnecessary to recover the full spectra of illuminant, rather it is sufficient to represent it by the projection of
from a given image, and then use this knowledge to recover an image which is independent of the scene illuminant. It is often unnecessary to recover the full spectra of illuminant, rather it is sufficient to represent it by the projection of 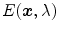 on RGB domain, i.e.
on RGB domain, i.e. ![$$\varvec{e}(\varvec{x}) = [e_R(\varvec{x}), e_G(\varvec{x}), e_B(\varvec{x})]^T$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_IEq28.gif) , where:
, where: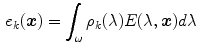
(7)
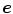 is an under-constrained problem. In practice, color constancy algorithms rely on various assumptions on statistical properties of the illuminant, and surface reflectance properties to estimate
is an under-constrained problem. In practice, color constancy algorithms rely on various assumptions on statistical properties of the illuminant, and surface reflectance properties to estimate 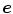 . One of the widely used assumptions is that the scene illumination is constant over the entire image and thus
. One of the widely used assumptions is that the scene illumination is constant over the entire image and thus 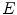 is simply a function of wavelength
is simply a function of wavelength 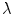 (i.e.
(i.e. 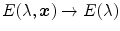 ).
).Once the illuminant 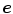 is estimated, then each RGB pixel value of the input image
is estimated, then each RGB pixel value of the input image ![$$\varvec{I}^i = [I_R^i,I_G^i,I_B^i]^T$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_IEq35.gif) is mapped to the corresponding pixel of the output image
is mapped to the corresponding pixel of the output image ![$$\varvec{I}^o = [I_R^o,I_G^o,I_B^o]^T$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_IEq36.gif) (under the canonical illuminant) by a transform matrix,
(under the canonical illuminant) by a transform matrix, 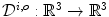 :
:
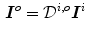
Further simplification can be done by restricting the transform matrix to a diagonal matrix. Assuming narrow-shaped sensor sensitivity functions (implying that sensor is sensitive only at a single wavelength, i.e. 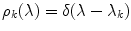 ), the RGB sensor response can be represented by
), the RGB sensor response can be represented by 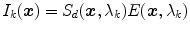 under Lambertian reflection model in (4). Let
under Lambertian reflection model in (4). Let 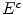 and
and 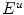 denote the canonical and the unknown illuminants, respectively, then the relationship between the RGB responses of two illuminants is:
denote the canonical and the unknown illuminants, respectively, then the relationship between the RGB responses of two illuminants is:
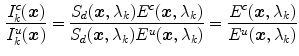
Consequently, the diagonal model maps the image taken under an unknown illuminant to the canonical counterpart simply by treating each channel independently:
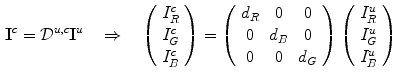
This model is closely related to the Von Kries hypothesis [53] which states that human color constancy is an independent gain regulation of the three cone photoreceptor signals through three different gain coefficients. Although (10) is derived for sensors with narrow spectral sensitivity function, it is a reasonably accurate model for general image sensors, and hence, this diagonal model is widely used in computational color constancy algorithms [41, 44].
 is estimated, then each RGB pixel value of the input image
is estimated, then each RGB pixel value of the input image ![$$\varvec{I}^i = [I_R^i,I_G^i,I_B^i]^T$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_IEq35.gif) is mapped to the corresponding pixel of the output image
is mapped to the corresponding pixel of the output image ![$$\varvec{I}^o = [I_R^o,I_G^o,I_B^o]^T$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_IEq36.gif) (under the canonical illuminant) by a transform matrix,
(under the canonical illuminant) by a transform matrix, 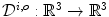 :
: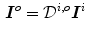
(8)
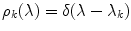 ), the RGB sensor response can be represented by
), the RGB sensor response can be represented by 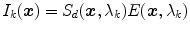 under Lambertian reflection model in (4). Let
under Lambertian reflection model in (4). Let 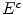 and
and 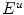 denote the canonical and the unknown illuminants, respectively, then the relationship between the RGB responses of two illuminants is:
denote the canonical and the unknown illuminants, respectively, then the relationship between the RGB responses of two illuminants is: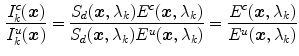
(9)
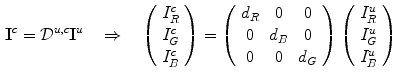
(10)
3.2 Existing Color Constancy Solutions
As mentioned earlier, color constancy is an under-constrained problem that scene illuminant (i.e. color of the light) cannot be estimated without any assumptions. Over the last several decades, a plethora of methods have been proposed with different underlying assumptions and implementation details. Comprehensive overviews are provided by Agarwal et al. [1], Gijsenij et al. [41], and Hordley [44]. Generally, prior art solutions can be divided into two classes (Table 1): (i) static approach, (ii) learning-based approach. Static approaches predict the illumination information solely based on the content in a single image with certain assumptions about the general nature of color images, while learning-based approach requires training data in order to build a statistical model prior to estimation of illumination.
Table 1
Summary of representative color constancy algorithms
Group | Subcategory | Methods |
|---|---|---|
Static approach | DRM based method | |
Low-level statistics based method | ||
Learning based approach | Probabilistic method | |
Gamut mapping method | Gamut mapping (Forsyth [28]), Improved gamut mapping (Barnard [3]), 2D chromaticity gamut mapping (Finlayson and Hordley [22]), Diagonal offset model gamut mapping (Finlayson et al. [21]), Color in perspective (Finlayson [19]), Edge based gamut mapping (Gijsenij et al. [40]), Gamut mapping using skin color (Bianco and Schettini [6]) | |
Fusion and selection based method | Combined physical and statistical (Schaefer et al. [60]), Committee-based (Cardei and Funt [13]), Consensus-based framework (Bianco et al. [8]), Natural image statistics (Gijsenij and Gevers [38]), Texture similarity (Bing et al. [52]), Indoor/outdoor classification (Bianco et al. [7]), Category correlation (Vazquez-Corral et al. [65]), Low-level feature combination (Bianco et al. [9]) |
3.2.1 Static Approaches
The static approaches can be further divided into two subclasses: (i) DRM based method, (ii) Lambertian model based method (low-level statistics method).
DRM Based Methods
DRM based method exploits physical knowledge of image formation to estimate the color of the scene illuminant. Commonly shared assumption by these methods is that RGB sensor values measured from different points on an inhomogeneous material (uniformly colored surface) will fall on a plane in RGB colorspace. In other words, the DRM in (3) can be restated as follows:
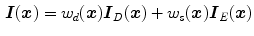
where ![$$\varvec{I}_D(\varvec{x}) = [I_{R,D}(\varvec{x}),I_{G,D}(\varvec{x}),I_{B,D}(\varvec{x})]^T$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_IEq42.gif) is the RGB response corresponding to diffuse reflection and
is the RGB response corresponding to diffuse reflection and ![$$\varvec{I}_E(\varvec{x}) = [I_{R,E}(\varvec{x}),I_{G,E}(\varvec{x}),I_{B,E}(\varvec{x})]^T$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_IEq43.gif) is the one corresponding to scene illuminant.4 According to (11), the RGB responses for a given surface reflectance and illuminant lie on a 2D plane (called a dichromatic plane), spanned by the two vectors
is the one corresponding to scene illuminant.4 According to (11), the RGB responses for a given surface reflectance and illuminant lie on a 2D plane (called a dichromatic plane), spanned by the two vectors 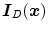 and
and 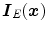 . If there are two distinct objects within the scene of constant illumination, two of such dichromatic planes can be obtained. Therefore, the vector representing the color of the illuminant can be estimated by intersecting two of these planes.
. If there are two distinct objects within the scene of constant illumination, two of such dichromatic planes can be obtained. Therefore, the vector representing the color of the illuminant can be estimated by intersecting two of these planes.
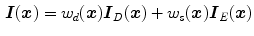
(11)
![$$\varvec{I}_D(\varvec{x}) = [I_{R,D}(\varvec{x}),I_{G,D}(\varvec{x}),I_{B,D}(\varvec{x})]^T$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_IEq42.gif) is the RGB response corresponding to diffuse reflection and
is the RGB response corresponding to diffuse reflection and ![$$\varvec{I}_E(\varvec{x}) = [I_{R,E}(\varvec{x}),I_{G,E}(\varvec{x}),I_{B,E}(\varvec{x})]^T$$](/wp-content/uploads/2016/03/A308467_1_En_3_Chapter_IEq43.gif) is the one corresponding to scene illuminant.4 According to (11), the RGB responses for a given surface reflectance and illuminant lie on a 2D plane (called a dichromatic plane), spanned by the two vectors
is the one corresponding to scene illuminant.4 According to (11), the RGB responses for a given surface reflectance and illuminant lie on a 2D plane (called a dichromatic plane), spanned by the two vectors 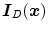 and
and 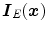 . If there are two distinct objects within the scene of constant illumination, two of such dichromatic planes can be obtained. Therefore, the vector representing the color of the illuminant can be estimated by intersecting two of these planes.
. If there are two distinct objects within the scene of constant illumination, two of such dichromatic planes can be obtained. Therefore, the vector representing the color of the illuminant can be estimated by intersecting two of these planes.Lee [50] proposed a simple DRM based method to compute the illuminant chromaticity by exploiting specular highlights of multiple surfaces in the scene (Identification of highlights in the scene is important since highlight areas exhibit significant contribution of surface reflection component). Instead of using RGB domain, the author identified pixels corresponds to highlight regions by projecting them into chromaticity space. From identified highlight pixels of more than two different colored surfaces (where each of pixel groups from a uniform surface yields a line segment in chromaticity space), the intersection point of the line segments is computed, which becomes the final estimate of the scene illuminant chromaticity. Similar approach is proposed by Tominaga and Wandell [64], where they exploited the singular-value decomposition (SVD) to determine a dichromatic plane from the spectral power distribution of inhomogeneous material. Although aforementioned methods provide simple solutions for characterizing the scene illuminant, they often yield suboptimal performance since the presence of small image noise dramatically affects the computation of the intersection in colorspace.
Finlayson and Schaefer [24] extended DRM based method by imposing a constraint on the colors of illumination. This method essentially adopts statistical knowledge that almost all natural and man-made illuminants fall close to the Planckian locus of black-body radiators in chromaticity space. Initially, highlight pixels are located from a uniformly colored surface to obtain a chromatic line segment in chromaticity space. Subsequently, the illuminant estimate is obtained by intersecting the dichromatic line with the Planckian locus. This method is beneficial over aforementioned methods since: (i) it present a novel scheme by combining physical model of image formation and statistical knowledge of plausible illuminants, (ii) the scene illuminant can be estimated even from a single surface, whereas aforementioned approaches requires at least two distinct surfaces.
Tan et al. [63] introduced the concept of inverse-intensity chromaticity (IIC) space for reliable estimation of scene illuminant chromaticity. Authors indicated that there is a linear relationship between the image chromaticity 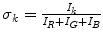 and the inverse-intensity
and the inverse-intensity 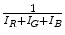 (
(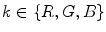 ), if pixels are taken from a uniformly colored surface. Based on this linear correlation, a novel color constancy method exploiting IIC space is presented. Similar to other DRM based methods, highlight pixels are initially identified from the input image and projected into IIC space. In IIC space,5 highlight pixels extracted from a uniformly colored object forms a line segment, and chromaticity of the scene illuminant can be estimated by finding the point where the line intersect with vertical axis of the IIC. One clear advantage of this method is that it is capable of handling both uniform and nonuniform surface color object in a single framework, without imposing strong constraints on illumination.
), if pixels are taken from a uniformly colored surface. Based on this linear correlation, a novel color constancy method exploiting IIC space is presented. Similar to other DRM based methods, highlight pixels are initially identified from the input image and projected into IIC space. In IIC space,5 highlight pixels extracted from a uniformly colored object forms a line segment, and chromaticity of the scene illuminant can be estimated by finding the point where the line intersect with vertical axis of the IIC. One clear advantage of this method is that it is capable of handling both uniform and nonuniform surface color object in a single framework, without imposing strong constraints on illumination.
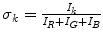 and the inverse-intensity
and the inverse-intensity 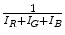 (
(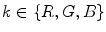 ), if pixels are taken from a uniformly colored surface. Based on this linear correlation, a novel color constancy method exploiting IIC space is presented. Similar to other DRM based methods, highlight pixels are initially identified from the input image and projected into IIC space. In IIC space,5 highlight pixels extracted from a uniformly colored object forms a line segment, and chromaticity of the scene illuminant can be estimated by finding the point where the line intersect with vertical axis of the IIC. One clear advantage of this method is that it is capable of handling both uniform and nonuniform surface color object in a single framework, without imposing strong constraints on illumination.
), if pixels are taken from a uniformly colored surface. Based on this linear correlation, a novel color constancy method exploiting IIC space is presented. Similar to other DRM based methods, highlight pixels are initially identified from the input image and projected into IIC space. In IIC space,5 highlight pixels extracted from a uniformly colored object forms a line segment, and chromaticity of the scene illuminant can be estimated by finding the point where the line intersect with vertical axis of the IIC. One clear advantage of this method is that it is capable of handling both uniform and nonuniform surface color object in a single framework, without imposing strong constraints on illumination.In general, DRM based solutions are advantageous since they are theoretically strong and require relatively fewer surfaces (i.e. reflectance statistics) than other methods to identify the scene illuminant. However, their performance typically depends on nontrivial preprocessing steps, such as identification of highlight pixels or segmentation, which are another challenging research questions. Moreover, pixel intensity of specular highlight content is often clipped due to limited dynamic range of sensor, turning it into an unreliable indicator of the scene illuminant. For these reasons, most of early works in this category focused on high-quality images of simple objects (i.e. no texture) taken under well-controlled laboratory conditions and rarely dealt with real world datasets of images [41, 44]. Recently, Drew et al. [16] presented a novel DRM based method which yields promising performance on real world datasets. Authors introduced the planar constraint that log-relative-chromaticity values6 for highlight pixels are orthogonal to the light chromaticity. This constraint indicates that the geometric mean of the pixels in highlight region is an important indicator for the scene illuminant. Authors claimed that this method yields comparable performance with other training based methods on both laboratory and real world data sets (e.g. Ciurea’s grayball dataset [14] and Gehler’s color checker dataset [32]).
Low-level Statistics Methods
On the other hand, low-level statistics methods, which are based on Lambertian reflection model, provide more practical means to deal with general web contents type of input. Buchsbaum [12] proposed the Grayworld (GW) algorithm which assumes that the spatial average of surface reflectances in a scene is achromatic (i.e. gray) under the canonical illuminant. The underlying logic behind GW algorithm is that since the surface color is random and independent, it is reasonable to assume that given a sufficient large number of samples, the average surface color should converge to gray. Thus, any deviation from achromaticity in the average scene color is caused by the effect of the scene illuminant. The GW is one of the most popular algorithms for color constancy due to its simplicity. Another popular color constancy method in this category is the White Patch (WP) algorithm (also known as max RGB) [30, 49] which assumes that the scene contains a surface with perfect reflectance property. Since a surface with this property reflects the full range of light, the color of the illuminant can be estimated by identifying a perfect reflectance surface. WP algorithm estimates the scene illuminant by computing the maximum intensity of each color channel.
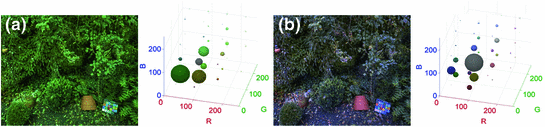
Although both GW and WP are well-known tractable solutions, their performances significantly deteriorate when the underlying assumptions are violated. The GW algorithm fails when the image contains large regions of uniform colors since it is unable to distinguish whether the dominant color in a scene is a superimposed cast due to the illuminant or an intrinsic color of the scene. For example, the average color of an image which contains an object in front of the dominant green background will be biased towards green rather than gray, even if it is taken under the canonical illuminant (Fig. 4). For such images, the dominant colors in a scene contribute to the shifted average color and GW algorithm will produce sub-optimal results (i.e. results in under or over-compensated output). Weijer et al. [70] proposed an extended GW hypothesis to address such issue: the average reflectance of semantic classes (such as sky, grass, road, and building) in an image is equal to the average reflectance color of that sematic class in the training dataset. Basically, this new hypothesis analyzes the input scene to assign a semantic class to it, and then, adaptively adjusts the target average color of the scene depending on the inferred semantic class. The drawback of WP algorithm is that a single maximum value may not be a reliable estimate of the scene illuminant, since the value can be contaminated by noise due to highlight. Instead of selecting the highest intensity directly, the stability of WP algorithm can be enhanced by choosing the intensity 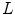 such that all pixels containing intensity higher than the selected one account for specific percentage of total number of pixels in the scene (e.g. the number of pixels with higher intensity than
such that all pixels containing intensity higher than the selected one account for specific percentage of total number of pixels in the scene (e.g. the number of pixels with higher intensity than 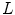 are less than
are less than 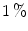 of total pixels) [17]. Another well-known cause for the failure of WP is a potential clipping issue of maximum intensity due to limited dynamic range of image acquisition devices. Funt and Shi [31] investigated this issue by evaluating WP algorithm on 105 high dynamic range (HDR) images generated by standard multiple exposure approach. Authors demonstrated that WP algorithm yields comparable performance to other advanced methods, e.g. Gray Edge [69], provided that image data preserve full dynamic range of the original scene and they are properly preprocessed (either by a media filtering or bicubic interpolation).
of total pixels) [17]. Another well-known cause for the failure of WP is a potential clipping issue of maximum intensity due to limited dynamic range of image acquisition devices. Funt and Shi [31] investigated this issue by evaluating WP algorithm on 105 high dynamic range (HDR) images generated by standard multiple exposure approach. Authors demonstrated that WP algorithm yields comparable performance to other advanced methods, e.g. Gray Edge [69], provided that image data preserve full dynamic range of the original scene and they are properly preprocessed (either by a media filtering or bicubic interpolation).
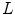 such that all pixels containing intensity higher than the selected one account for specific percentage of total number of pixels in the scene (e.g. the number of pixels with higher intensity than
such that all pixels containing intensity higher than the selected one account for specific percentage of total number of pixels in the scene (e.g. the number of pixels with higher intensity than 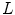 are less than
are less than 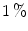 of total pixels) [17]. Another well-known cause for the failure of WP is a potential clipping issue of maximum intensity due to limited dynamic range of image acquisition devices. Funt and Shi [31] investigated this issue by evaluating WP algorithm on 105 high dynamic range (HDR) images generated by standard multiple exposure approach. Authors demonstrated that WP algorithm yields comparable performance to other advanced methods, e.g. Gray Edge [69], provided that image data preserve full dynamic range of the original scene and they are properly preprocessed (either by a media filtering or bicubic interpolation).
of total pixels) [17]. Another well-known cause for the failure of WP is a potential clipping issue of maximum intensity due to limited dynamic range of image acquisition devices. Funt and Shi [31] investigated this issue by evaluating WP algorithm on 105 high dynamic range (HDR) images generated by standard multiple exposure approach. Authors demonstrated that WP algorithm yields comparable performance to other advanced methods, e.g. Gray Edge [69], provided that image data preserve full dynamic range of the original scene and they are properly preprocessed (either by a media filtering or bicubic interpolation).
Fig. 4
An example illustrating the failure of Grayworld color constancy solution (sample image is taken from [32]). 3D RGB histograms are presented to demonstrate the distribution of color values. a Original image. b Image corrected by Grayworld
Recently, several attempts have been made to generalize color constancy algorithms under a unified framework, such as Shades of Gray (SoG) [25] and Gray Edge (GE) [69]. Especially, GE algorithm by Weijer et al. [69] not only generalizes existing works but also extends color constancy methods to incorporate derivative information, i.e. edges and higher order statistics (Recall that aforementioned GW and WP algorithms use pixel intensity values to estimate the scene illuminant). GE is based on the hypothesis that the average of the reflectance differences in a scene is achromatic. This hypothesis is originated from the observation that the color derivative of images under white light sources are relatively densely distributed along with the axis coincides with the white light axis [68].
Under GE assumption, Weijer et al. [69] presented a single combined framework of color constancy technique to estimate the color of light source 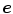 based on both RGB pixel value and low-level image features (i.e. derivatives) as follows:
based on both RGB pixel value and low-level image features (i.e. derivatives) as follows:
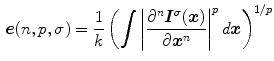
where 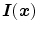 is the RGB sensor response of two-dimensional spatial coordinates
is the RGB sensor response of two-dimensional spatial coordinates 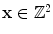 , and
, and 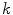 is a constant so that the
is a constant so that the 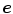 has a unit length. The framework of (12) covers a wide range of color constancy algorithms using three variables
has a unit length. The framework of (12) covers a wide range of color constancy algorithms using three variables 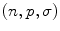 in Table 2. Selection of proper parameter values for Gray Edge framework is highly important to yield good color constancy accuracy (See Sect. 5.1 for further detail).
in Table 2. Selection of proper parameter values for Gray Edge framework is highly important to yield good color constancy accuracy (See Sect. 5.1 for further detail).
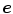 based on both RGB pixel value and low-level image features (i.e. derivatives) as follows:
based on both RGB pixel value and low-level image features (i.e. derivatives) as follows: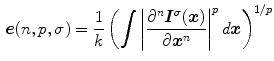
(12)
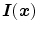 is the RGB sensor response of two-dimensional spatial coordinates
is the RGB sensor response of two-dimensional spatial coordinates 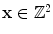 , and
, and 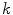 is a constant so that the
is a constant so that the 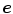 has a unit length. The framework of (12) covers a wide range of color constancy algorithms using three variables
has a unit length. The framework of (12) covers a wide range of color constancy algorithms using three variables 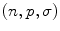 in Table 2. Selection of proper parameter values for Gray Edge framework is highly important to yield good color constancy accuracy (See Sect. 5.1 for further detail).
in Table 2. Selection of proper parameter values for Gray Edge framework is highly important to yield good color constancy accuracy (See Sect. 5.1 for further detail).Parameters | Description |
|---|---|
Order of structure 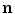 | Defines if the method is based on the pixel intensity or based on the spatial derivatives of order 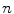 . For example, . For example, 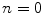 is for pixel based methods (e.g. GW and WP), while is for pixel based methods (e.g. GW and WP), while 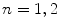 is for 1st/2nd order GE methods is for 1st/2nd order GE methods |
Minkowski norm 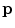 | Determines the relative weights of the multiple measurements from which the final illuminant color is estimated. For example, 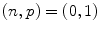 is GW, is GW, 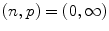 is WP, and is WP, and 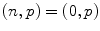 is SoG is SoG |
Local averaging scale 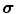 | Applying local averaging prior to illuminant estimation allows for the reduction of noise effect in illuminant estimation [37]. 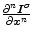 is equal to is equal to 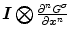 , where , where 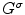 is a Gaussian filter with the standard deviation is a Gaussian filter with the standard deviation 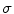 |
In general, low-level statistics based methods are known to yield acceptable performance (inferior to methods based on extensive training data or complex assumptions) at low computational cost, and thus are suitable for practical applications dealing with real-world images.
3.2.2 Learning Based Approaches
The second type of color constancy algorithms estimate the scene illuminant using a model that is learned on training data. Three main subcategories include: (i) gamut mapping method, (ii) probabilistic method, (iii) fusion and selection based method.
Gamut Mapping Methods
The gamut mapping color constancy algorithms, introduced by Forsyth [28], rely on an assumption that the range of color measurements in real-world images are restricted on a given illuminant. The limited set of colors that can occur under a given illuminant is called the canonical gamut 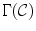 which can be estimated by collecting a large selection of objects with different reflectances illuminated with one known light source (i.e canonical illuminant).
which can be estimated by collecting a large selection of objects with different reflectances illuminated with one known light source (i.e canonical illuminant).
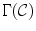 which can be estimated by collecting a large selection of objects with different reflectances illuminated with one known light source (i.e canonical illuminant).
which can be estimated by collecting a large selection of objects with different reflectances illuminated with one known light source (i.e canonical illuminant).
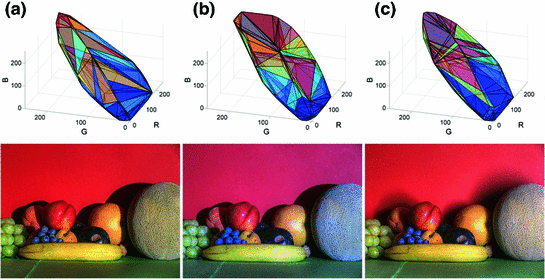
Fig. 5
Variations of RGB image gamut of the sample scene [5] under three different illuminants. a Solux 3500 (spectra similar to daylight of 3500 K). b Sylvania 50MR16Q  blue filter (incandescent light). c Sylvania cool white (fluorescent light)
blue filter (incandescent light). c Sylvania cool white (fluorescent light)
 blue filter (incandescent light). c Sylvania cool white (fluorescent light)
blue filter (incandescent light). c Sylvania cool white (fluorescent light)A key component of gamut mapping algorithm is the definition of a canonical gamut 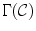 , which denotes the convex set of RGB sensor responses
, which denotes the convex set of RGB sensor responses 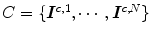 to
to 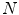 surface reflectances under a canonical illuminant
surface reflectances under a canonical illuminant 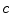 :
:
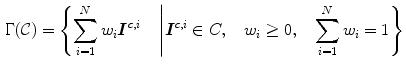
The image gamut 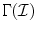 is defined in a similar way from the set of RGB values from input image. If
is defined in a similar way from the set of RGB values from input image. If 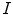 is the set of RGB responses recorded under the unknown illumination, then all convex combinations of
is the set of RGB responses recorded under the unknown illumination, then all convex combinations of 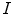 denoted
denoted 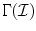 could occur under the unknown illuminant. Because only a limited number of surfaces is observed within a single image, the unknown gamut can only be approximated by the observed image gamut (Fig. 5). The next stage of gamut mapping is to find all transform matrices
could occur under the unknown illuminant. Because only a limited number of surfaces is observed within a single image, the unknown gamut can only be approximated by the observed image gamut (Fig. 5). The next stage of gamut mapping is to find all transform matrices 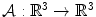 such that:
such that:
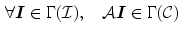
where 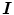 is a tri-vector RGB responses. A transform matrix
is a tri-vector RGB responses. A transform matrix 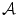 (as shown in (10), a diagonal matrix is assumed) is a possible solution to 14 if it maps the
(as shown in (10), a diagonal matrix is assumed) is a possible solution to 14 if it maps the 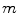 -th point in the image gamut
-th point in the image gamut 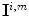 to any point within the canonical gamut. For individual point on the convex hull of the image gamut, there exists a set of mappings taking this point to a point on the convex hull of the canonical gamut, denoted as
to any point within the canonical gamut. For individual point on the convex hull of the image gamut, there exists a set of mappings taking this point to a point on the convex hull of the canonical gamut, denoted as 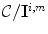 . Then the set of all convex combinations of
. Then the set of all convex combinations of 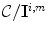 , denoted
, denoted 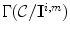 , can be defined as the set of all mappings taking
, can be defined as the set of all mappings taking 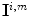 into point within the canonical gamut. A point in this set represents the diagonal components of a diagonal matrix
into point within the canonical gamut. A point in this set represents the diagonal components of a diagonal matrix 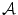 , mapping
, mapping 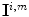 to a point
to a point 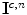 in the canonical gamut:
in the canonical gamut:
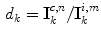
where 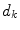 represents the diagonal components of a diagonal matrix
represents the diagonal components of a diagonal matrix 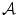 (See (10)
(See (10) 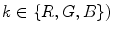 . For each point in the image gamut, there is a corresponding set of diagonal mappings representing possible illuminants under which this surface could have been viewed. Therefore, the intersection of all these mapping sets, denoted
. For each point in the image gamut, there is a corresponding set of diagonal mappings representing possible illuminants under which this surface could have been viewed. Therefore, the intersection of all these mapping sets, denoted 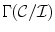 , is the set of mappings corresponds to a possible illuminant:
, is the set of mappings corresponds to a possible illuminant:
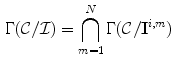
Once set of all possible mapping from 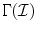 to
to 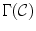 is calculated then the mapping that transforms the given image gamut to a maximally large gamut (in volume) within the canonical gamut is selected as the final solution. Alternative approach is proposed in [3] by using the weighted average of the feasible set. A limitation of the original gamut mapping method is that it may produce an empty set of feasible mapping
is calculated then the mapping that transforms the given image gamut to a maximally large gamut (in volume) within the canonical gamut is selected as the final solution. Alternative approach is proposed in [3] by using the weighted average of the feasible set. A limitation of the original gamut mapping method is that it may produce an empty set of feasible mapping 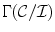 under certain conditions. Finlayson et al. [21
under certain conditions. Finlayson et al. [21




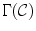 , which denotes the convex set of RGB sensor responses
, which denotes the convex set of RGB sensor responses 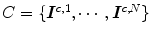 to
to 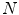 surface reflectances under a canonical illuminant
surface reflectances under a canonical illuminant 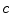 :
: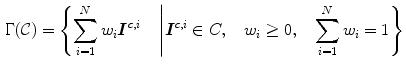
(13)
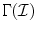 is defined in a similar way from the set of RGB values from input image. If
is defined in a similar way from the set of RGB values from input image. If 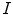 is the set of RGB responses recorded under the unknown illumination, then all convex combinations of
is the set of RGB responses recorded under the unknown illumination, then all convex combinations of 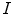 denoted
denoted 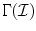 could occur under the unknown illuminant. Because only a limited number of surfaces is observed within a single image, the unknown gamut can only be approximated by the observed image gamut (Fig. 5). The next stage of gamut mapping is to find all transform matrices
could occur under the unknown illuminant. Because only a limited number of surfaces is observed within a single image, the unknown gamut can only be approximated by the observed image gamut (Fig. 5). The next stage of gamut mapping is to find all transform matrices 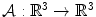 such that:
such that: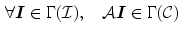
(14)
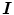 is a tri-vector RGB responses. A transform matrix
is a tri-vector RGB responses. A transform matrix 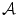 (as shown in (10), a diagonal matrix is assumed) is a possible solution to 14 if it maps the
(as shown in (10), a diagonal matrix is assumed) is a possible solution to 14 if it maps the 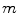 -th point in the image gamut
-th point in the image gamut 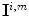 to any point within the canonical gamut. For individual point on the convex hull of the image gamut, there exists a set of mappings taking this point to a point on the convex hull of the canonical gamut, denoted as
to any point within the canonical gamut. For individual point on the convex hull of the image gamut, there exists a set of mappings taking this point to a point on the convex hull of the canonical gamut, denoted as 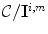 . Then the set of all convex combinations of
. Then the set of all convex combinations of 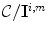 , denoted
, denoted 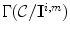 , can be defined as the set of all mappings taking
, can be defined as the set of all mappings taking 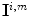 into point within the canonical gamut. A point in this set represents the diagonal components of a diagonal matrix
into point within the canonical gamut. A point in this set represents the diagonal components of a diagonal matrix 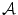 , mapping
, mapping 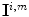 to a point
to a point 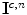 in the canonical gamut:
in the canonical gamut: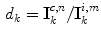
(15)
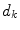 represents the diagonal components of a diagonal matrix
represents the diagonal components of a diagonal matrix 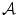 (See (10)
(See (10) 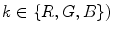 . For each point in the image gamut, there is a corresponding set of diagonal mappings representing possible illuminants under which this surface could have been viewed. Therefore, the intersection of all these mapping sets, denoted
. For each point in the image gamut, there is a corresponding set of diagonal mappings representing possible illuminants under which this surface could have been viewed. Therefore, the intersection of all these mapping sets, denoted 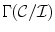 , is the set of mappings corresponds to a possible illuminant:
, is the set of mappings corresponds to a possible illuminant: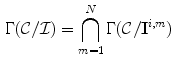
(16)
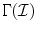 to
to 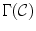 is calculated then the mapping that transforms the given image gamut to a maximally large gamut (in volume) within the canonical gamut is selected as the final solution. Alternative approach is proposed in [3] by using the weighted average of the feasible set. A limitation of the original gamut mapping method is that it may produce an empty set of feasible mapping
is calculated then the mapping that transforms the given image gamut to a maximally large gamut (in volume) within the canonical gamut is selected as the final solution. Alternative approach is proposed in [3] by using the weighted average of the feasible set. A limitation of the original gamut mapping method is that it may produce an empty set of feasible mapping 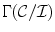 under certain conditions. Finlayson et al. [21
under certain conditions. Finlayson et al. [21
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree




