be an Euclidean or digital space (i.e. 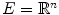 or
or 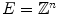 with
with 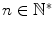 ). Let
). Let 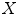 be a subset of
be a subset of 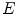 . Let
. Let 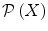 denote the class of all subsets of
denote the class of all subsets of 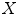 :
: 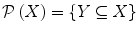 . Let
. Let 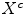 denote the complement of
denote the complement of 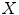 , i.e. the set of all points of
, i.e. the set of all points of 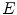 that do not belong to
that do not belong to 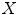 :
: 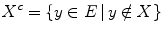 . Let
. Let 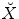 denote the reflection of
denote the reflection of 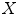 , i.e. the set
, i.e. the set 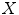 transformed by a central symmetry:
transformed by a central symmetry: 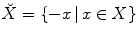 . Finally, we will denote by
. Finally, we will denote by 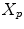 the translate of
the translate of 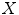 by
by 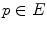 defined by
defined by 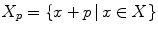 .
.
The basic operators of erosion and dilation of 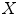 by the Structuring Element (SE)
by the Structuring Element (SE) 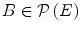 are written respectively
are written respectively 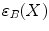 and
and 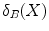 . They are defined using the Minkowski subtraction (
. They are defined using the Minkowski subtraction ( ) and addition (
) and addition ( ):
):
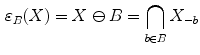
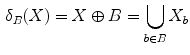
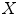 by the Structuring Element (SE)
by the Structuring Element (SE) 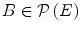 are written respectively
are written respectively 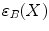 and
and 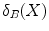 . They are defined using the Minkowski subtraction (
. They are defined using the Minkowski subtraction ( ) and addition (
) and addition (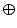 ):
):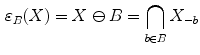
(1)
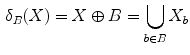
(2)
2.2 Binary HMT
Being given a subset 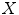 of
of 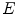 , the principle of the HMT is to look for all positions
, the principle of the HMT is to look for all positions 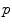 in
in 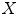 where a structuring element
where a structuring element 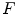 called the foreground fits in the shape (
called the foreground fits in the shape (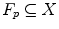 ) while another structuring element
) while another structuring element 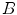 called the background fits in the complement of
called the background fits in the complement of 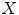 (
(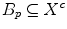 ). The HMT of
). The HMT of 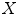 by the structuring elements
by the structuring elements 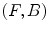 , noted
, noted 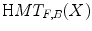 , can be defined in terms of Minkowski subtraction and addition (structuring erosion and dilation):
, can be defined in terms of Minkowski subtraction and addition (structuring erosion and dilation):
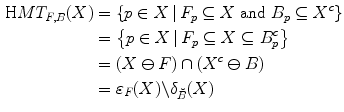
A direct consequence of this definition is that if 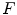 and
and 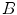 have a non-empty intersection, then
have a non-empty intersection, then 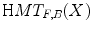 is empty for all
is empty for all 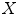 in
in 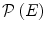 (a given pixel cannot simultaneously belongs to the foreground and to the background). One can also note that: first, the second formulation of (Eq. 3) is known as the interval operator from [15] and second, the complementation does not appear in the last formulation which allows to naturally extend the HMT to gray-level images where complementation is not defined.
(a given pixel cannot simultaneously belongs to the foreground and to the background). One can also note that: first, the second formulation of (Eq. 3) is known as the interval operator from [15] and second, the complementation does not appear in the last formulation which allows to naturally extend the HMT to gray-level images where complementation is not defined.
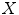 of
of 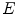 , the principle of the HMT is to look for all positions
, the principle of the HMT is to look for all positions 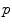 in
in 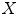 where a structuring element
where a structuring element 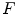 called the foreground fits in the shape (
called the foreground fits in the shape (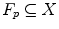 ) while another structuring element
) while another structuring element 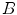 called the background fits in the complement of
called the background fits in the complement of 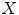 (
(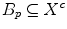 ). The HMT of
). The HMT of 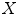 by the structuring elements
by the structuring elements 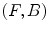 , noted
, noted 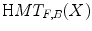 , can be defined in terms of Minkowski subtraction and addition (structuring erosion and dilation):
, can be defined in terms of Minkowski subtraction and addition (structuring erosion and dilation):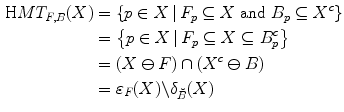
(3)
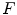 and
and 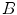 have a non-empty intersection, then
have a non-empty intersection, then 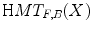 is empty for all
is empty for all 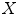 in
in 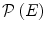 (a given pixel cannot simultaneously belongs to the foreground and to the background). One can also note that: first, the second formulation of (Eq. 3) is known as the interval operator from [15] and second, the complementation does not appear in the last formulation which allows to naturally extend the HMT to gray-level images where complementation is not defined.
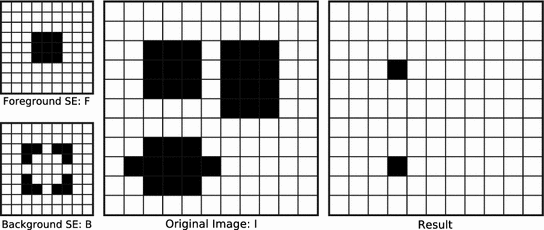
(a given pixel cannot simultaneously belongs to the foreground and to the background). One can also note that: first, the second formulation of (Eq. 3) is known as the interval operator from [15] and second, the complementation does not appear in the last formulation which allows to naturally extend the HMT to gray-level images where complementation is not defined.Figure 1 illustrates the application of the hit-or-miss transform on a binary image. Our goal here is to detect 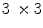 squares with possible extensions along edges. It is noteworthy that the two structuring elements do not need to cover the whole neighborhood of a pixel and some pixels, as the middle of the edges of the square, can be excluded from the decision process by neither putting them in
squares with possible extensions along edges. It is noteworthy that the two structuring elements do not need to cover the whole neighborhood of a pixel and some pixels, as the middle of the edges of the square, can be excluded from the decision process by neither putting them in 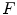 nor in
nor in 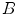 . This is a first attempt to ensure robustness to uncertainty or noise. Some more advanced solutions, not specific to binary images will be reviewed in Sec. 5.
. This is a first attempt to ensure robustness to uncertainty or noise. Some more advanced solutions, not specific to binary images will be reviewed in Sec. 5.
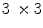 squares with possible extensions along edges. It is noteworthy that the two structuring elements do not need to cover the whole neighborhood of a pixel and some pixels, as the middle of the edges of the square, can be excluded from the decision process by neither putting them in
squares with possible extensions along edges. It is noteworthy that the two structuring elements do not need to cover the whole neighborhood of a pixel and some pixels, as the middle of the edges of the square, can be excluded from the decision process by neither putting them in 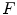 nor in
nor in 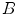 . This is a first attempt to ensure robustness to uncertainty or noise. Some more advanced solutions, not specific to binary images will be reviewed in Sec. 5.
. This is a first attempt to ensure robustness to uncertainty or noise. Some more advanced solutions, not specific to binary images will be reviewed in Sec. 5.
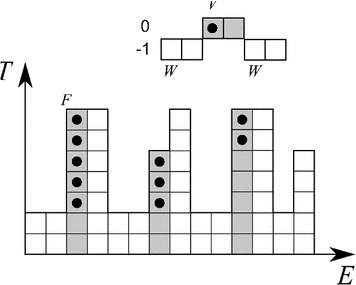
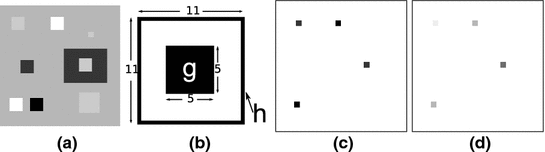
Fig. 1
Example of application of binary HMT to detect 3 x 3 squares with possible extensions along edges [27]. The pixels belonging to the images are in black while those belonging to the complement are in white. The top left image represents the foreground SE: 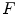 , origin of the image is at the centre of the square. The bottom left image is the background SE
, origin of the image is at the centre of the square. The bottom left image is the background SE 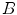 , with same origin as
, with same origin as 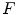 . The middle image is the original image
. The middle image is the original image 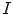 . And the right image is the result of the HMT applied on
. And the right image is the result of the HMT applied on 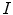 with SEs
with SEs 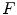 and
and 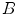
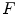 , origin of the image is at the centre of the square. The bottom left image is the background SE
, origin of the image is at the centre of the square. The bottom left image is the background SE 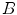 , with same origin as
, with same origin as 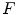 . The middle image is the original image
. The middle image is the original image 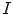 . And the right image is the result of the HMT applied on
. And the right image is the result of the HMT applied on 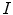 with SEs
with SEs 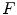 and
and 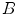
3 Template Matching in Grayscale Images
We recall here basics of Mathematical Morphology in the grayscale case, with adequate definitions and notations. The various definitions of the HMT on grayscale images (e.g.,[8, 23, 31, 34]) will then be presented and discussed, with comprehensive examples.
3.1 Grayscale Mathematical Morphology
We now consider the case of grayscale images, i.e.of mappings from 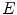 to the set of values
to the set of values 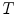 (
( ). Moreover, we assume that
). Moreover, we assume that 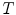 is a complete lattice, i.e. a non empty set equipped with a partial ordering
is a complete lattice, i.e. a non empty set equipped with a partial ordering 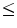 , an infimum
, an infimum 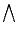 and a supremum
and a supremum 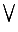 such that the infimum and supremum of any non empty subset of
such that the infimum and supremum of any non empty subset of 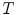 belongs to
belongs to 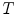 (for all
(for all  ,
,  and
and 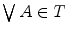 ). The lattice
). The lattice 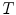 is thus bounded by its least element
is thus bounded by its least element 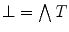 and its greatest element
and its greatest element 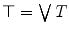 . For grayscale images we usually take
. For grayscale images we usually take 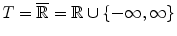 or
or 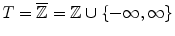 . The notion of structuring element naturally extends to the one of structuring function (SF) which is simply an element of
. The notion of structuring element naturally extends to the one of structuring function (SF) which is simply an element of 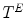 .
.
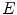 to the set of values
to the set of values 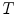 (
(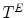 ). Moreover, we assume that
). Moreover, we assume that 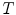 is a complete lattice, i.e. a non empty set equipped with a partial ordering
is a complete lattice, i.e. a non empty set equipped with a partial ordering 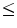 , an infimum
, an infimum 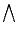 and a supremum
and a supremum 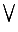 such that the infimum and supremum of any non empty subset of
such that the infimum and supremum of any non empty subset of  belongs to
belongs to  (for all
(for all 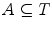 ,
, 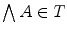 and
and 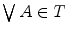 ). The lattice
). The lattice 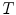 is thus bounded by its least element
is thus bounded by its least element 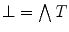 and its greatest element
and its greatest element 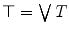 . For grayscale images we usually take
. For grayscale images we usually take 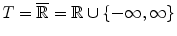 or
or 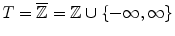 . The notion of structuring element naturally extends to the one of structuring function (SF) which is simply an element of
. The notion of structuring element naturally extends to the one of structuring function (SF) which is simply an element of 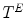 .
.The definitions of the binary erosion (Eq. 1) and binary dilation (Eq. 2) then naturally extend to grayscale images. Let 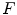 in
in 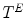 be a grayscale image and
be a grayscale image and 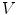 in
in 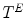 be a structuring function. The grayscale erosion
be a structuring function. The grayscale erosion 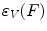 and dilation
and dilation 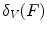 of
of 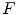 by
by 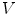 are then defined for all
are then defined for all 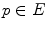 by:
by:
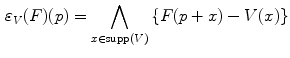
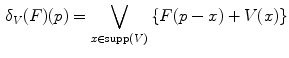
where 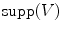 is the support of
is the support of 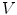 , i.e.the set of points of
, i.e.the set of points of 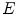 where
where 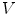 is greater than the least element
is greater than the least element 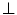 :
: 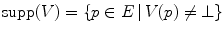 . These formulas can lead to disinclination like
. These formulas can lead to disinclination like 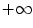 plus
plus 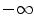 . To keep consistency
. To keep consistency 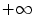 plus
plus 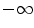 must be valued as
must be valued as 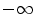 in Eq. 5 and as
in Eq. 5 and as 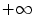 in Eq. 4.
in Eq. 4.
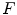 in
in 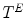 be a grayscale image and
be a grayscale image and 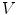 in
in 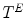 be a structuring function. The grayscale erosion
be a structuring function. The grayscale erosion 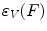 and dilation
and dilation 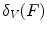 of
of 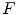 by
by 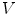 are then defined for all
are then defined for all 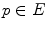 by:
by: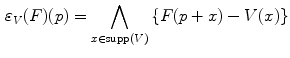
(4)
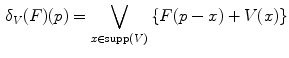
(5)
 is the support of
is the support of 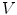 , i.e.the set of points of
, i.e.the set of points of 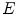 where
where 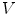 is greater than the least element
is greater than the least element 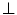 :
: 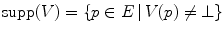 . These formulas can lead to disinclination like
. These formulas can lead to disinclination like 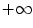 plus
plus 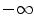 . To keep consistency
. To keep consistency 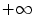 plus
plus 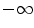 must be valued as
must be valued as 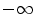 in Eq. 5 and as
in Eq. 5 and as 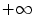 in Eq. 4.
in Eq. 4.3.2 Grayscale HMT
The binary HMT was first extended to grayscale images by Ronse [31] and then many other definitions followed: by Shaefer [32], Khosravi [18], Raducanu [29], Soille [36], Barat [7], Perret [27]. A recent survey on grayscale HMT is given in [22]. These various definitions have been recently unified into a common theoretical framework for graylevel interval operators [23]. In the binary case, the interval operator (second line of Eq. 3) looks for each translation 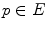 if the image fits between the background SE translated at
if the image fits between the background SE translated at 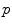 and the complement of the background SE also translated at
and the complement of the background SE also translated at 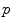 . In the grayscale case, the sought template is translated not only horizontally (by a point
. In the grayscale case, the sought template is translated not only horizontally (by a point 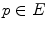 ), but vertically as well (by a finite graylevel
), but vertically as well (by a finite graylevel 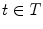 ) in an attempt to detect the positions where it fits (Fig. 2). Specifically, we will note
) in an attempt to detect the positions where it fits (Fig. 2). Specifically, we will note 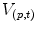 the translation of
the translation of 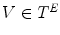 by a couple
by a couple 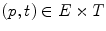 : for all
: for all 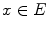 ,
, 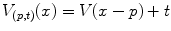 .
.
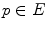 if the image fits between the background SE translated at
if the image fits between the background SE translated at 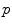 and the complement of the background SE also translated at
and the complement of the background SE also translated at 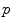 . In the grayscale case, the sought template is translated not only horizontally (by a point
. In the grayscale case, the sought template is translated not only horizontally (by a point 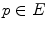 ), but vertically as well (by a finite graylevel
), but vertically as well (by a finite graylevel 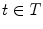 ) in an attempt to detect the positions where it fits (Fig. 2). Specifically, we will note
) in an attempt to detect the positions where it fits (Fig. 2). Specifically, we will note 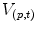 the translation of
the translation of 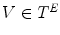 by a couple
by a couple 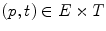 : for all
: for all 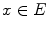 ,
, 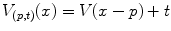 .
.According to the unified theory for grayscale HMT [23], a grayscale HMT is decomposed into two stages:
Let us observe that in the binary case, the fitted pixels are the ones retained by the HMT, and their valuation is simply equal to one (or foreground).
the fitting, where the locations fitting the given structuring functions, describing the sought template, are computed,
and valuation, where the resulting image containing the previously detected locations is constructed.
3.2.1 Fitting
We first describe the different fittings. Let 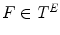 be a grayscale image and
be a grayscale image and 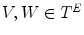 be a couple of structuring functions describing the sought template such that
be a couple of structuring functions describing the sought template such that 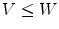 . Formally a fitting is a mapping from
. Formally a fitting is a mapping from 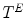 into
into 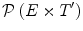 where
where 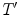 can be a subset of
can be a subset of 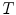 or any set of values. A first fitting involved in Ronse’s HMT is given by:
or any set of values. A first fitting involved in Ronse’s HMT is given by:
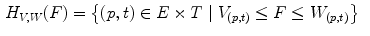
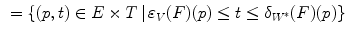
where 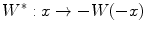 , is the dual of
, is the dual of 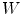 .
. 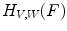 is thus the set of all translations where the image lies between both structuring functions (Fig. 3).
is thus the set of all translations where the image lies between both structuring functions (Fig. 3).
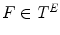 be a grayscale image and
be a grayscale image and 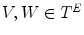 be a couple of structuring functions describing the sought template such that
be a couple of structuring functions describing the sought template such that 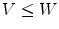 . Formally a fitting is a mapping from
. Formally a fitting is a mapping from 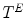 into
into 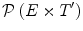 where
where  can be a subset of
can be a subset of  or any set of values. A first fitting involved in Ronse’s HMT is given by:
or any set of values. A first fitting involved in Ronse’s HMT is given by: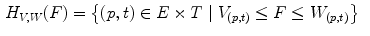
(6)
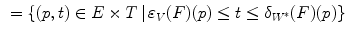
(7)
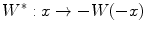 , is the dual of
, is the dual of 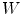 .
. 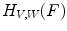 is thus the set of all translations where the image lies between both structuring functions (Fig. 3).
is thus the set of all translations where the image lies between both structuring functions (Fig. 3).
Fig. 3
Illustration of 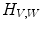 (Eq. (6)). We consider a function
(Eq. (6)). We consider a function  from
from 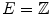 into
into 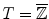 and the two structuring functions
and the two structuring functions 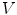 and
and 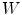 (the origin is on the left pixel of
(the origin is on the left pixel of 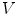 ). The result of
). The result of 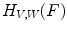 is the set of points of
is the set of points of 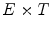 marked by a black circle inside
marked by a black circle inside 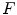 . We also give the result of the application of the supremal valuation (Eq. (12)) of
. We also give the result of the application of the supremal valuation (Eq. (12)) of 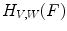 in gray, i.e. the result of
in gray, i.e. the result of 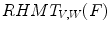 (Eq. (14)).
(Eq. (14)).
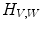 (Eq. (6)). We consider a function
(Eq. (6)). We consider a function  from
from 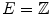 into
into 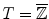 and the two structuring functions
and the two structuring functions 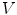 and
and 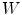 (the origin is on the left pixel of
(the origin is on the left pixel of 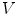 ). The result of
). The result of 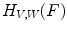 is the set of points of
is the set of points of 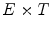 marked by a black circle inside
marked by a black circle inside 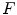 . We also give the result of the application of the supremal valuation (Eq. (12)) of
. We also give the result of the application of the supremal valuation (Eq. (12)) of 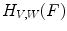 in gray, i.e. the result of
in gray, i.e. the result of 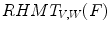 (Eq. (14)).
(Eq. (14)).A second fitting, involved in Soille’s and Barat’s HMT is:
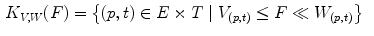
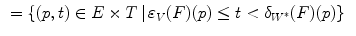
where 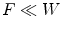 means that there is some
means that there is some 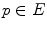 we have
we have 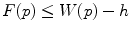 .
. 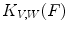 is thus the set of all translations where the image lies between both structuring functions and does not touch
is thus the set of all translations where the image lies between both structuring functions and does not touch 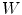 (Fig. 4).
(Fig. 4).
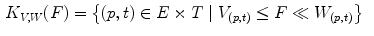
(8)
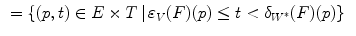
(9)
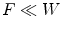 means that there is some
means that there is some 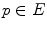 we have
we have 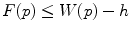 .
. 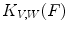 is thus the set of all translations where the image lies between both structuring functions and does not touch
is thus the set of all translations where the image lies between both structuring functions and does not touch 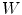 (Fig. 4).
(Fig. 4).
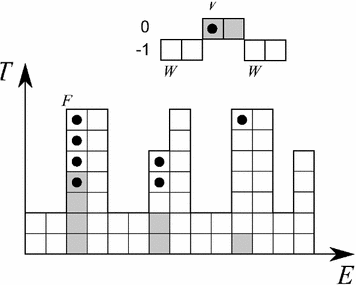
Fig. 4
Illustration of 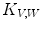 (Eq. 8). We consider a function
(Eq. 8). We consider a function 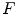 from
from 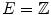 into
into 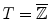 and the two structuring functions
and the two structuring functions 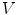 and
and 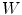 (the origin is on the left pixel of
(the origin is on the left pixel of 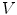 ). The result of
). The result of 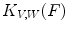 is the set of points of
is the set of points of 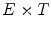 marked by a black circle inside
marked by a black circle inside 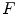 . We also give the result of the application of the integral valuation (Eq. 13) of
. We also give the result of the application of the integral valuation (Eq. 13) of 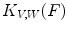 in gray, i.e. the result of
in gray, i.e. the result of 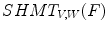 (Eq. 15)
(Eq. 15)
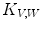 (Eq. 8). We consider a function
(Eq. 8). We consider a function  from
from 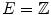 into
into 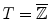 and the two structuring functions
and the two structuring functions 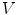 and
and 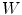 (the origin is on the left pixel of
(the origin is on the left pixel of 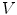 ). The result of
). The result of 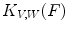 is the set of points of
is the set of points of 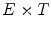 marked by a black circle inside
marked by a black circle inside 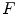 . We also give the result of the application of the integral valuation (Eq. 13) of
. We also give the result of the application of the integral valuation (Eq. 13) of 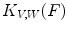 in gray, i.e. the result of
in gray, i.e. the result of 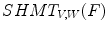 (Eq. 15)
(Eq. 15)
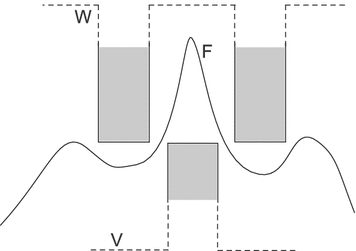
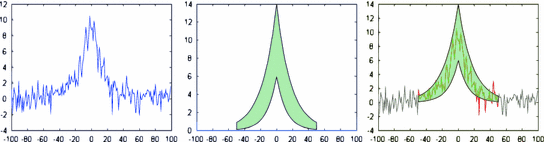
Fig. 5
Example of application of the 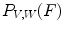 (Eq. 10) to detect an exponential profile with Gaussian noise [27]. The first image represents a 1D noisy signal. The second image represents the uncertainty area defined by the 2 SFs
(Eq. 10) to detect an exponential profile with Gaussian noise [27]. The first image represents a 1D noisy signal. The second image represents the uncertainty area defined by the 2 SFs 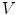 (lower function) and
(lower function) and 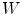 (upper function). The third image shows how well the pattern can fit the signal
(upper function). The third image shows how well the pattern can fit the signal
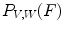 (Eq. 10) to detect an exponential profile with Gaussian noise [27]. The first image represents a 1D noisy signal. The second image represents the uncertainty area defined by the 2 SFs
(Eq. 10) to detect an exponential profile with Gaussian noise [27]. The first image represents a 1D noisy signal. The second image represents the uncertainty area defined by the 2 SFs 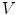 (lower function) and
(lower function) and 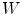 (upper function). The third image shows how well the pattern can fit the signal
(upper function). The third image shows how well the pattern can fit the signalFinally, a third fitting involved in Perret’s HMT is given by:
![$$\begin{aligned} P_{V,W}(F) = \left\{ \left( p,\textstyle {\frac{ |\left\{ q \in S \, | \, V(q)+t\le F(p+q)\le W(q)+t\right\} | }{|S|}}\right) \in E \times \left[ 0,1\right] ~\big |~ t\in T\right\} \end{aligned}$$](/wp-content/uploads/2016/03/A308467_1_En_8_Chapter_Equ10.gif)
where 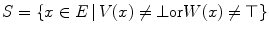 and
and 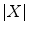 is the cardinal of the set
is the cardinal of the set 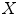 . Hence,
. Hence, 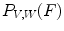 does not look for locations where both structuring functions completely fit the image. Instead, it measures at each location how well both structuring functions fit the image by counting, among the points of the image that lies in the support of one of the SF, the ratio of points that fits between both SF (Fig. 5).
does not look for locations where both structuring functions completely fit the image. Instead, it measures at each location how well both structuring functions fit the image by counting, among the points of the image that lies in the support of one of the SF, the ratio of points that fits between both SF (Fig. 5).
![$$\begin{aligned} P_{V,W}(F) = \left\{ \left( p,\textstyle {\frac{ |\left\{ q \in S \, | \, V(q)+t\le F(p+q)\le W(q)+t\right\} | }{|S|}}\right) \in E \times \left[ 0,1\right] ~\big |~ t\in T\right\} \end{aligned}$$](/wp-content/uploads/2016/03/A308467_1_En_8_Chapter_Equ10.gif)
(10)
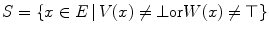 and
and 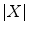 is the cardinal of the set
is the cardinal of the set 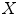 . Hence,
. Hence, 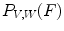 does not look for locations where both structuring functions completely fit the image. Instead, it measures at each location how well both structuring functions fit the image by counting, among the points of the image that lies in the support of one of the SF, the ratio of points that fits between both SF (Fig. 5).
does not look for locations where both structuring functions completely fit the image. Instead, it measures at each location how well both structuring functions fit the image by counting, among the points of the image that lies in the support of one of the SF, the ratio of points that fits between both SF (Fig. 5).3.2.2 Valuation
Likewise, there are several types of valuations. Formally, a valuation 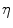 is a mapping that associates a (grayscale) image (
is a mapping that associates a (grayscale) image (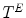 ) to any result of a fitting
) to any result of a fitting 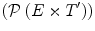 . Let
. Let 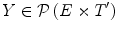 , the simplest valuation
, the simplest valuation 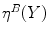 , the binary valuation, consists in taking the set of points
, the binary valuation, consists in taking the set of points 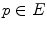 for which there is at least one
for which there is at least one 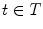 such that
such that 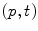 belongs to
belongs to 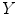 .
.
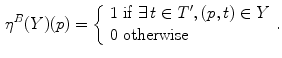
Another valuation is the supremal valuation 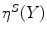 , which for every point
, which for every point 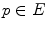 of fit couples
of fit couples 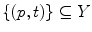 , takes the supremum of
, takes the supremum of 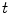 (Fig. 3):
(Fig. 3):
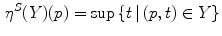
Finally there is the integral valuation 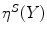 which instead for every point
which instead for every point 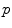 of fit couples
of fit couples 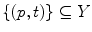 , uses the length of the interval of
, uses the length of the interval of 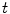 for which the couples
for which the couples 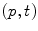 fit (Fig. 4).
fit (Fig. 4).
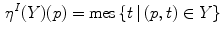
where 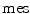 is an appropriate measure of intervals in
is an appropriate measure of intervals in 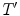 (simply the Lebesgue measure if
(simply the Lebesgue measure if 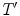 is an interval of
is an interval of 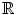 or
or 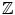 ).
).
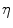 is a mapping that associates a (grayscale) image (
is a mapping that associates a (grayscale) image (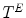 ) to any result of a fitting
) to any result of a fitting 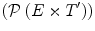 . Let
. Let 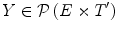 , the simplest valuation
, the simplest valuation 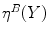 , the binary valuation, consists in taking the set of points
, the binary valuation, consists in taking the set of points 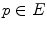 for which there is at least one
for which there is at least one 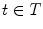 such that
such that 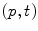 belongs to
belongs to 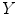 .
.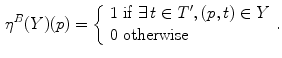
(11)
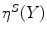 , which for every point
, which for every point 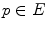 of fit couples
of fit couples 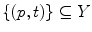 , takes the supremum of
, takes the supremum of 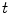 (Fig. 3):
(Fig. 3):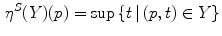
(12)
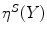 which instead for every point
which instead for every point 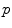 of fit couples
of fit couples 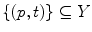 , uses the length of the interval of
, uses the length of the interval of 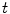 for which the couples
for which the couples 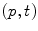 fit (Fig. 4).
fit (Fig. 4).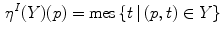
(13)
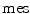 is an appropriate measure of intervals in
is an appropriate measure of intervals in 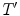 (simply the Lebesgue measure if
(simply the Lebesgue measure if  is an interval of
is an interval of 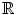 or
or 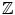 ).
).3.3 HMT Definitions
The different combinations of fittings and valuations allow to recover the different definitions of HMT. Let 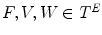 with
with 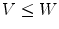 and
and 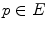 , among others, we mention:
, among others, we mention:
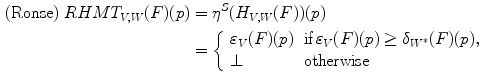
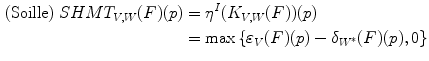
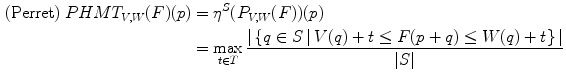
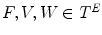 with
with  and
and  , among others, we mention:
, among others, we mention: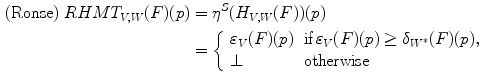
(14)
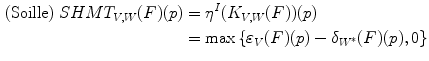
(15)
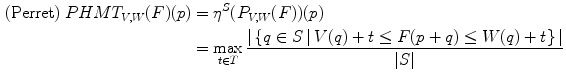
(16)

Fig. 6
Grayscale HMT : a original image ( pixels); b couple of structuring functions used within the HMT; c result with Ronse’s, d and Soille’s definition (results are displayed in inverse gray levels and for the sake of clarity,
pixels); b couple of structuring functions used within the HMT; c result with Ronse’s, d and Soille’s definition (results are displayed in inverse gray levels and for the sake of clarity, 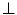 value was replaced with
value was replaced with 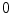 ) [39]
) [39]
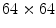 pixels); b couple of structuring functions used within the HMT; c result with Ronse’s, d and Soille’s definition (results are displayed in inverse gray levels and for the sake of clarity,
pixels); b couple of structuring functions used within the HMT; c result with Ronse’s, d and Soille’s definition (results are displayed in inverse gray levels and for the sake of clarity, 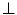 value was replaced with
value was replaced with 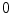 ) [39]
) [39]4 Template Matching in Color and Multivariate Images
The extension of the HMT to color and more generally to multivariate images such as multi- and hyper-spectral data, can amplify the application potential of the operator at a significant level. Of particular importance in this context are applications regarding color object detection from color data, target detection from remote sensing data, as well as the detection of challenging celestial objects from astronomical imaging sources.
However, given the multitude of existing approaches for the definition of the grayscale HMT, it is no surprise that the situation is no less clearer with multivariate images. In fact, conversely to grayscale morphological image processing, there is not even a generally accepted color mathematical morphology framework, let alone a standardized multivariate HMT. Nevertheless, the increasingly widespread availability of multivariate images, especially in the context of remote sensing, as well as recent advances in color morphology, have provided the missing impetus that has led to the intensification of the research work on extending the HMT to color, multi- and hyper-spectral data.
We will start this section by first recalling the basic theoretical implications of using multivariate images to the mathematical morphology theory, and elaborate on the difficulties of its extension to this type of images. Then, we will present the different methods that have been developed especially in the past few years for applying the HMT to multivariate images.
4.1 Multivariate Mathematical Morphology
According to the lattice based approach to mathematical morphology [30], digital images are represented as mappings 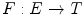 between the discrete coordinate grid
between the discrete coordinate grid 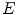 and the set of pixel values
and the set of pixel values 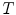 , with
, with 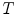 being a complete lattice. More precisely, imposing a complete lattice structure on an arbitrary set of pixel values
being a complete lattice. More precisely, imposing a complete lattice structure on an arbitrary set of pixel values 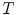 is possible, if
is possible, if 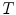 is equipped with at least a partial ordering relation which enables the computation of the infimum and supremum of any non-empty subset of
is equipped with at least a partial ordering relation which enables the computation of the infimum and supremum of any non-empty subset of 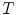 . Consequently, the morphological operators can be in fact applied to any type of image data, as long as the set of pixel values
. Consequently, the morphological operators can be in fact applied to any type of image data, as long as the set of pixel values 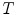 possesses a complete lattice structure. For a detailed account of multivariate morphology the reader is referred to Refs. [14, 33].
possesses a complete lattice structure. For a detailed account of multivariate morphology the reader is referred to Refs. [14, 33].
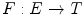 between the discrete coordinate grid
between the discrete coordinate grid 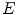 and the set of pixel values
and the set of pixel values 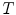 , with
, with 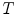 being a complete lattice. More precisely, imposing a complete lattice structure on an arbitrary set of pixel values
being a complete lattice. More precisely, imposing a complete lattice structure on an arbitrary set of pixel values 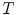 is possible, if
is possible, if 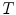 is equipped with at least a partial ordering relation which enables the computation of the infimum and supremum of any non-empty subset of
is equipped with at least a partial ordering relation which enables the computation of the infimum and supremum of any non-empty subset of 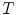 . Consequently, the morphological operators can be in fact applied to any type of image data, as long as the set of pixel values
. Consequently, the morphological operators can be in fact applied to any type of image data, as long as the set of pixel values 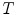 possesses a complete lattice structure. For a detailed account of multivariate morphology the reader is referred to Refs. [14, 33].
possesses a complete lattice structure. For a detailed account of multivariate morphology the reader is referred to Refs. [14, 33].For instance, in the case of continuous multidimensional grayscale images where 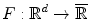 , it suffices to employ the usual comparison operator
, it suffices to employ the usual comparison operator 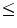 , in order to induce a complete lattice structure on
, in order to induce a complete lattice structure on 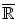 . Likewise, the inclusion operator
. Likewise, the inclusion operator 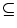 can be used with binary images
can be used with binary images 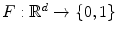 . However, if we now consider multivariate images
. However, if we now consider multivariate images 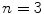 for the specific case of color images, it becomes problematic to find an ordering relation for the vectors of
for the specific case of color images, it becomes problematic to find an ordering relation for the vectors of 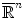 , due to the fact that there is no universal method for ordering multivariate data. As a result, in the last 15 years several ordering approaches have been explored with the end of extending mathematical morphology to multivariate images, for a detailed survey of which the reader is referred to Ref. [2].
, due to the fact that there is no universal method for ordering multivariate data. As a result, in the last 15 years several ordering approaches have been explored with the end of extending mathematical morphology to multivariate images, for a detailed survey of which the reader is referred to Ref. [2].
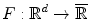 , it suffices to employ the usual comparison operator
, it suffices to employ the usual comparison operator 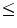 , in order to induce a complete lattice structure on
, in order to induce a complete lattice structure on 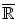 . Likewise, the inclusion operator
. Likewise, the inclusion operator 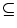 can be used with binary images
can be used with binary images 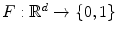 . However, if we now consider multivariate images
. However, if we now consider multivariate images 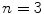 for the specific case of color images, it becomes problematic to find an ordering relation for the vectors of
for the specific case of color images, it becomes problematic to find an ordering relation for the vectors of 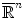 , due to the fact that there is no universal method for ordering multivariate data. As a result, in the last 15 years several ordering approaches have been explored with the end of extending mathematical morphology to multivariate images, for a detailed survey of which the reader is referred to Ref. [2].
, due to the fact that there is no universal method for ordering multivariate data. As a result, in the last 15 years several ordering approaches have been explored with the end of extending mathematical morphology to multivariate images, for a detailed survey of which the reader is referred to Ref. [2].We briefly recall the main properties of an ordering, i.e.a binary relation 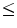 on a set
on a set 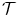 being reflexive (
being reflexive (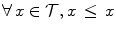 ), anti-symmetric (
), anti-symmetric (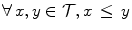 and
and 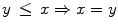 ), and transitive (
), and transitive (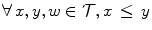 and
and 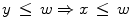 ). An ordering is total if the totality statement (
). An ordering is total if the totality statement (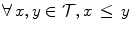 or
or 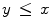 ) holds, partial otherwise. It is a pre-ordering if the anti-symmetry statement does not hold.
) holds, partial otherwise. It is a pre-ordering if the anti-symmetry statement does not hold.
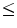 on a set
on a set 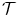 being reflexive (
being reflexive (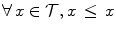 ), anti-symmetric (
), anti-symmetric (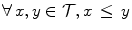 and
and 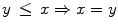 ), and transitive (
), and transitive (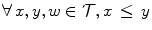 and
and 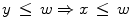 ). An ordering is total if the totality statement (
). An ordering is total if the totality statement (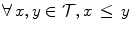 or
or 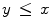 ) holds, partial otherwise. It is a pre-ordering if the anti-symmetry statement does not hold.
) holds, partial otherwise. It is a pre-ordering if the anti-symmetry statement does not hold.Hence, the HMT being a morphological tool, its extension to multivariate images also requires the implication of a vector ordering. We will now proceed to examine various solutions developed for applying the HMT to color or to multivariate data in general.
4.2 HMT Based on a Vector Ordering
Aptoula et al. [6] provide the first study on the theoretical requirements of a vector HMT (VHMT). In detail, the initial step for extending the HMT to multivariate data, consists in defining the erosion and dilation operators for multivariate images in combination with multivariate structuring functions (SF). More precisely, these operators are based on horizontal translations (by a point 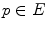 ) as well as on vertical ones (by a finite pixel value
) as well as on vertical ones (by a finite pixel value 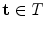 ) as in the grayscale case, the difference is however that pixel values are now multi-dimensional; in particular, given a multivariate image
) as in the grayscale case, the difference is however that pixel values are now multi-dimensional; in particular, given a multivariate image 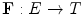 :
:
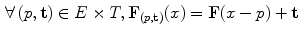
Furthermore, according to the fundamental Refs. [16, 17] of Heijmans and Ronse, translations need to be complete lattice automorphisms (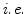 bijections
bijections 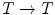 that preserve order, and whose inverse also preserve order). Consequently, the vector ordering
that preserve order, and whose inverse also preserve order). Consequently, the vector ordering 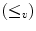 from which the complete lattice is derived, must be translation invariant. In other words:
from which the complete lattice is derived, must be translation invariant. In other words:
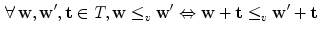
Thus one can give the definition of the erosion and dilation respectively of a multivariate image F by a multivariate SF B:
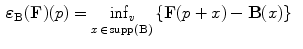




 ) as well as on vertical ones (by a finite pixel value
) as well as on vertical ones (by a finite pixel value  ) as in the grayscale case, the difference is however that pixel values are now multi-dimensional; in particular, given a multivariate image
) as in the grayscale case, the difference is however that pixel values are now multi-dimensional; in particular, given a multivariate image 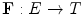 :
: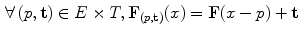
(17)
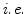 bijections
bijections 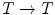 that preserve order, and whose inverse also preserve order). Consequently, the vector ordering
that preserve order, and whose inverse also preserve order). Consequently, the vector ordering 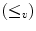 from which the complete lattice is derived, must be translation invariant. In other words:
from which the complete lattice is derived, must be translation invariant. In other words: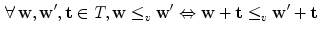
(18)
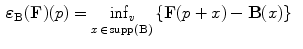
(19)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree