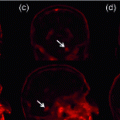
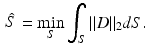Fig. 1.
Dictionary-based appearance learning and segmentation of post-surgical cortical brain surface in CT images for direct non-rigid registration of with pre-surgical MRI. We use a training set of post-implantation CT image to learn two models of image appearance, one inside the cortical surface and one outside. We then use these models to segment the cortical surface from test CT images. Using the extracted post-op surface, we perform surface-based registration with the pre-op MRI in order to co-visualize post-implantation electrodes with pre-op imaging data.
2 Methods
From a clinical database of 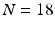 epilepsy patients at our institution, we have a set of images
epilepsy patients at our institution, we have a set of images 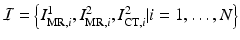 , where
, where 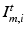 denotes pre-op images acquired at time
denotes pre-op images acquired at time 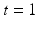 and post-op images acquired at time
and post-op images acquired at time 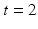 using imaging modality m for patient i. Following the current practice, for each patient we (i) create pre-op and post-op brain surfaces
using imaging modality m for patient i. Following the current practice, for each patient we (i) create pre-op and post-op brain surfaces 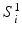 and
and 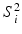 from the MR images by extracting isosurfaces of the brain masks generated by using the Brain Extraction Tool (BET) [14], (ii) rigidly register
from the MR images by extracting isosurfaces of the brain masks generated by using the Brain Extraction Tool (BET) [14], (ii) rigidly register 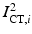 to
to 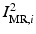 to produce the transformation
to produce the transformation 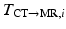 by maximizing the normalized mutual information (NMI) similarity metric [16], and (iii) non-rigidly register
by maximizing the normalized mutual information (NMI) similarity metric [16], and (iii) non-rigidly register 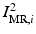 to
to 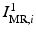 using a free-form deformation (FFD) [13] with 30 mm B-spline control point spacing and maximizing their NMI to produce the transformation
using a free-form deformation (FFD) [13] with 30 mm B-spline control point spacing and maximizing their NMI to produce the transformation 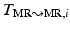 . We make use of this data to train our model of brain surface appearance in post-surgical CT images.
. We make use of this data to train our model of brain surface appearance in post-surgical CT images.
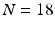 epilepsy patients at our institution, we have a set of images
epilepsy patients at our institution, we have a set of images 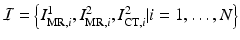 , where
, where 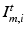 denotes pre-op images acquired at time
denotes pre-op images acquired at time 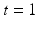 and post-op images acquired at time
and post-op images acquired at time 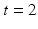 using imaging modality m for patient i. Following the current practice, for each patient we (i) create pre-op and post-op brain surfaces
using imaging modality m for patient i. Following the current practice, for each patient we (i) create pre-op and post-op brain surfaces 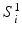 and
and 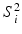 from the MR images by extracting isosurfaces of the brain masks generated by using the Brain Extraction Tool (BET) [14], (ii) rigidly register
from the MR images by extracting isosurfaces of the brain masks generated by using the Brain Extraction Tool (BET) [14], (ii) rigidly register 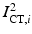 to
to 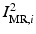 to produce the transformation
to produce the transformation 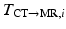 by maximizing the normalized mutual information (NMI) similarity metric [16], and (iii) non-rigidly register
by maximizing the normalized mutual information (NMI) similarity metric [16], and (iii) non-rigidly register 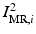 to
to 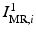 using a free-form deformation (FFD) [13] with 30 mm B-spline control point spacing and maximizing their NMI to produce the transformation
using a free-form deformation (FFD) [13] with 30 mm B-spline control point spacing and maximizing their NMI to produce the transformation 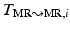 . We make use of this data to train our model of brain surface appearance in post-surgical CT images.
. We make use of this data to train our model of brain surface appearance in post-surgical CT images.2.1 Oriented Local Image Appearance
Let 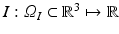 be the 3D image that maps points from the spatial domain
be the 3D image that maps points from the spatial domain 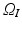 to image intensity values. We define the set of intensities in an orientable local image patch
to image intensity values. We define the set of intensities in an orientable local image patch 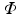 centered about
centered about 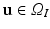 :
:
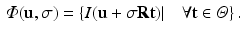
Here, 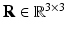 is a rotation matrix consisting of a set of orthonormal basis vectors and
is a rotation matrix consisting of a set of orthonormal basis vectors and 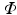 is a set of d image intensity values sampled at patch template points
is a set of d image intensity values sampled at patch template points 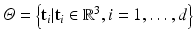 , whose physical size is controlled by a scale term
, whose physical size is controlled by a scale term 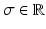 . Typically, standard image patches are aligned with the image axes such that
. Typically, standard image patches are aligned with the image axes such that 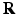 uses the standard basis
uses the standard basis 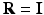 , the identity matrix, and
, the identity matrix, and 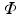 consists of an isotropic grid of sample points centered about the patch origin. For example, a
consists of an isotropic grid of sample points centered about the patch origin. For example, a 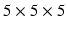 isotropic image patch
isotropic image patch 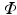 consists of
consists of 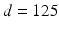 sample points
sample points 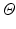 arranged in a grid about the patch origin.
arranged in a grid about the patch origin.
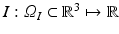 be the 3D image that maps points from the spatial domain
be the 3D image that maps points from the spatial domain 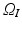 to image intensity values. We define the set of intensities in an orientable local image patch
to image intensity values. We define the set of intensities in an orientable local image patch 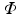 centered about
centered about 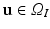 :
: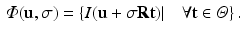
(1)
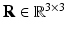 is a rotation matrix consisting of a set of orthonormal basis vectors and
is a rotation matrix consisting of a set of orthonormal basis vectors and 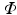 is a set of d image intensity values sampled at patch template points
is a set of d image intensity values sampled at patch template points 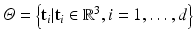 , whose physical size is controlled by a scale term
, whose physical size is controlled by a scale term 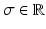 . Typically, standard image patches are aligned with the image axes such that
. Typically, standard image patches are aligned with the image axes such that 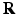 uses the standard basis
uses the standard basis 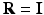 , the identity matrix, and
, the identity matrix, and 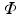 consists of an isotropic grid of sample points centered about the patch origin. For example, a
consists of an isotropic grid of sample points centered about the patch origin. For example, a 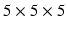 isotropic image patch
isotropic image patch 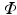 consists of
consists of 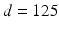 sample points
sample points  arranged in a grid about the patch origin.
arranged in a grid about the patch origin.In this work, we use oriented image patches, where the orientation of the patch 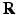 is determined by the data. Since we are interested in building a model of image appearance both inside and outside the brain surface, we orient image patches according to local surface geometry. For each point on the surface of interest
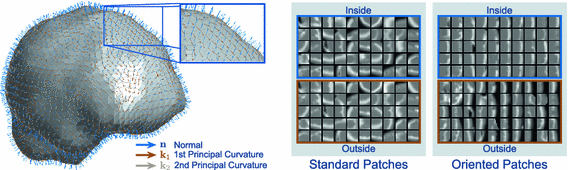
is determined by the data. Since we are interested in building a model of image appearance both inside and outside the brain surface, we orient image patches according to local surface geometry. For each point on the surface of interest 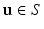 , we compute the local surface normal
, we compute the local surface normal 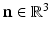 and the directions of principal curvature
and the directions of principal curvature 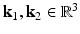 [6]. These normalized vectors form an orthonormal basis
[6]. These normalized vectors form an orthonormal basis ![$$\mathbf{R}=\left[ \mathbf{n}|\mathbf{k}_1 |\mathbf{k}_2 \right] $$](/wp-content/uploads/2016/09/A339424_1_En_52_Chapter_IEq33.gif) with which we orient the patch
with which we orient the patch 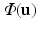 in (1). Figure 2 provides an illustrative comparison between standard and oriented patches at corresponding points along a surface
in (1). Figure 2 provides an illustrative comparison between standard and oriented patches at corresponding points along a surface  . By orienting the patches in this manner, the texture patterns in our patches exhibit greater invariance to changes in location along the surface S.
. By orienting the patches in this manner, the texture patterns in our patches exhibit greater invariance to changes in location along the surface S.
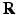 is determined by the data. Since we are interested in building a model of image appearance both inside and outside the brain surface, we orient image patches according to local surface geometry. For each point on the surface of interest
is determined by the data. Since we are interested in building a model of image appearance both inside and outside the brain surface, we orient image patches according to local surface geometry. For each point on the surface of interest 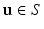 , we compute the local surface normal
, we compute the local surface normal 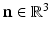 and the directions of principal curvature
and the directions of principal curvature 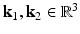 [6]. These normalized vectors form an orthonormal basis
[6]. These normalized vectors form an orthonormal basis ![$$\mathbf{R}=\left[ \mathbf{n}|\mathbf{k}_1 |\mathbf{k}_2 \right] $$](/wp-content/uploads/2016/09/A339424_1_En_52_Chapter_IEq33.gif) with which we orient the patch
with which we orient the patch 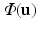 in (1). Figure 2 provides an illustrative comparison between standard and oriented patches at corresponding points along a surface
in (1). Figure 2 provides an illustrative comparison between standard and oriented patches at corresponding points along a surface 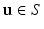 . By orienting the patches in this manner, the texture patterns in our patches exhibit greater invariance to changes in location along the surface S.
. By orienting the patches in this manner, the texture patterns in our patches exhibit greater invariance to changes in location along the surface S.
Fig. 2.
Examples of local oriented image patches compared to their corresponding standard local image patches oriented along the image axes. For the surface S, the local surface normal 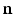 and directions of principal curvature
and directions of principal curvature 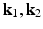 define a local orthonormal basis by which we orient the image patches. We show patch examples from both inside and outside the cortical surface.
define a local orthonormal basis by which we orient the image patches. We show patch examples from both inside and outside the cortical surface.
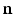 and directions of principal curvature
and directions of principal curvature 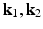 define a local orthonormal basis by which we orient the image patches. We show patch examples from both inside and outside the cortical surface.
define a local orthonormal basis by which we orient the image patches. We show patch examples from both inside and outside the cortical surface.2.2 Training the Cortical Surface Appearance Model
To learn our model of brain boundary appearance, we first map the segmented post-op brain surface to the post-op CT image space, 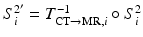 , where
, where 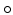 is the transformation operator. We then create a sparse representation model
is the transformation operator. We then create a sparse representation model 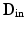 (dictionary) of the intensities inside of the brain and a model
(dictionary) of the intensities inside of the brain and a model 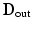 of the region just outside the brain [9]. These dictionaries will capture the varieties of textural appearance found near the brain surface boundary. We create these models by extracting a training set of overlapping local image patches inside,
of the region just outside the brain [9]. These dictionaries will capture the varieties of textural appearance found near the brain surface boundary. We create these models by extracting a training set of overlapping local image patches inside, 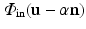 , and outside,
, and outside, 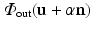 , points on the surface
, points on the surface 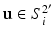 , where
, where 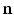 is the outward facing local surface normal and
is the outward facing local surface normal and 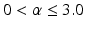 mm defines a narrow band region. As in Sect. 2.1, we use the local surface geometry at
mm defines a narrow band region. As in Sect. 2.1, we use the local surface geometry at 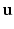 to orient the image patches.
to orient the image patches.
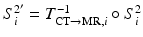 , where
, where  is the transformation operator. We then create a sparse representation model
is the transformation operator. We then create a sparse representation model 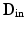 (dictionary) of the intensities inside of the brain and a model
(dictionary) of the intensities inside of the brain and a model 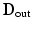 of the region just outside the brain [9]. These dictionaries will capture the varieties of textural appearance found near the brain surface boundary. We create these models by extracting a training set of overlapping local image patches inside,
of the region just outside the brain [9]. These dictionaries will capture the varieties of textural appearance found near the brain surface boundary. We create these models by extracting a training set of overlapping local image patches inside, 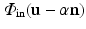 , and outside,
, and outside, 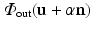 , points on the surface
, points on the surface 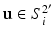 , where
, where 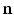 is the outward facing local surface normal and
is the outward facing local surface normal and 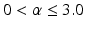 mm defines a narrow band region. As in Sect. 2.1, we use the local surface geometry at
mm defines a narrow band region. As in Sect. 2.1, we use the local surface geometry at 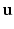 to orient the image patches.
to orient the image patches.For each appearance class 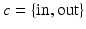 , we create appearance vectors
, we create appearance vectors 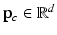 for each image patch by concatenating the patch values from the set
for each image patch by concatenating the patch values from the set 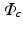 , where d is the sample dimensionality determined by the chosen patch sampling template
, where d is the sample dimensionality determined by the chosen patch sampling template  in Sect. 2.1, and normalize
in Sect. 2.1, and normalize 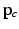 to have unit length. Then, we model the distribution of
to have unit length. Then, we model the distribution of 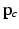 ’s from all N training images using an overcomplete dictionary
’s from all N training images using an overcomplete dictionary 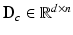 such that
such that 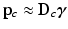 [1]. Here, n is the number of dictionary atoms and
[1]. Here, n is the number of dictionary atoms and 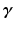 is the sparse dictionary weighting coefficients. To reconstruct a given appearance sample
is the sparse dictionary weighting coefficients. To reconstruct a given appearance sample 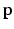 (normalized to have unit length) from the dictionary with a given target sparsity constraint
(normalized to have unit length) from the dictionary with a given target sparsity constraint 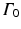 , we solve the sparse coding problem
, we solve the sparse coding problem
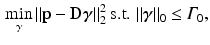
using an orthogonal matching pursuit (OMP) algorithm [12]. Next, we define the residual error
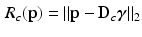
for both the inside and outside region classes. Using normalized appearance vectors, 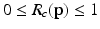 , where values of 0 correspond to perfect signal reconstruction (strong membership to class c) and values of 1 indicate
, where values of 0 correspond to perfect signal reconstruction (strong membership to class c) and values of 1 indicate 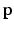 could not be reconstructed by
could not be reconstructed by 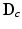 (poor membership to class c). Intuitively,
(poor membership to class c). Intuitively, 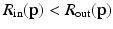 for points inside the cortical surface boundary. In contrast to Huang et al. [9]’s multi-scale modeling where multi-scale data is concatenated into appearance vectors, we perform this sampling and training procedure individually for each level
for points inside the cortical surface boundary. In contrast to Huang et al. [9]’s multi-scale modeling where multi-scale data is concatenated into appearance vectors, we perform this sampling and training procedure individually for each level 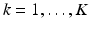 in a multi-resolution Gaussian image pyramid, which means that we train K dictionary pairs
in a multi-resolution Gaussian image pyramid, which means that we train K dictionary pairs 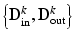 .
.
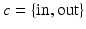 , we create appearance vectors
, we create appearance vectors 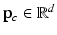 for each image patch by concatenating the patch values from the set
for each image patch by concatenating the patch values from the set 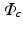 , where d is the sample dimensionality determined by the chosen patch sampling template
, where d is the sample dimensionality determined by the chosen patch sampling template 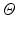 in Sect. 2.1, and normalize
in Sect. 2.1, and normalize 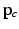 to have unit length. Then, we model the distribution of
to have unit length. Then, we model the distribution of 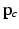 ’s from all N training images using an overcomplete dictionary
’s from all N training images using an overcomplete dictionary 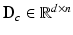 such that
such that 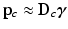 [1]. Here, n is the number of dictionary atoms and
[1]. Here, n is the number of dictionary atoms and 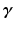 is the sparse dictionary weighting coefficients. To reconstruct a given appearance sample
is the sparse dictionary weighting coefficients. To reconstruct a given appearance sample 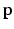 (normalized to have unit length) from the dictionary with a given target sparsity constraint
(normalized to have unit length) from the dictionary with a given target sparsity constraint 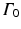 , we solve the sparse coding problem
, we solve the sparse coding problem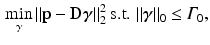
(2)
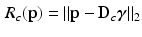
(3)
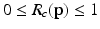 , where values of 0 correspond to perfect signal reconstruction (strong membership to class c) and values of 1 indicate
, where values of 0 correspond to perfect signal reconstruction (strong membership to class c) and values of 1 indicate 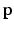 could not be reconstructed by
could not be reconstructed by 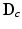 (poor membership to class c). Intuitively,
(poor membership to class c). Intuitively, 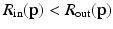 for points inside the cortical surface boundary. In contrast to Huang et al. [9]’s multi-scale modeling where multi-scale data is concatenated into appearance vectors, we perform this sampling and training procedure individually for each level
for points inside the cortical surface boundary. In contrast to Huang et al. [9]’s multi-scale modeling where multi-scale data is concatenated into appearance vectors, we perform this sampling and training procedure individually for each level 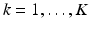 in a multi-resolution Gaussian image pyramid, which means that we train K dictionary pairs
in a multi-resolution Gaussian image pyramid, which means that we train K dictionary pairs 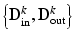 .
.2.3 Segmenting the Cortical Surface in Post-implantation CT Images
Given a new pair of pre-implantation MRI and post-implantation CT test images not in the training set  , we perform an initial brain surface segmentation estimate
, we perform an initial brain surface segmentation estimate 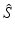 using an intensity-based rigid registration of
using an intensity-based rigid registration of 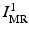 and
and 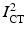 and transforming the segmented MR surface
and transforming the segmented MR surface 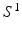 to post-op imaging space, i.e.
to post-op imaging space, i.e. 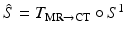 . For a point on the estimated surface
. For a point on the estimated surface 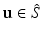 , we extract the oriented local image patch
, we extract the oriented local image patch 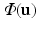 to create the appearance vector
to create the appearance vector 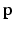 , and then compute the difference of the appearance model residuals from (3) such that
, and then compute the difference of the appearance model residuals from (3) such that
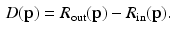
Intuitively, if 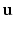 lies within the true boundary of the cortical surface in the CT image then
lies within the true boundary of the cortical surface in the CT image then ![$$D(\mathbf{p})>0$$” src=”/wp-content/uploads/2016/09/A339424_1_En_52_Chapter_IEq75.gif”></SPAN>, and if <SPAN id=IEq76 class=InlineEquation><IMG alt=$$\mathbf{u}$$ src=]() is outside the true boundary then
is outside the true boundary then 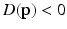 . Thus, the cortical surface boundary is located at the point
. Thus, the cortical surface boundary is located at the point 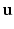 where
where 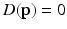 . We therefore seek the surface that minimizes the objective function
. We therefore seek the surface that minimizes the objective function
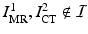 , we perform an initial brain surface segmentation estimate
, we perform an initial brain surface segmentation estimate 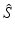 using an intensity-based rigid registration of
using an intensity-based rigid registration of 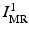 and
and 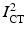 and transforming the segmented MR surface
and transforming the segmented MR surface 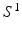 to post-op imaging space, i.e.
to post-op imaging space, i.e. 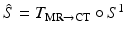 . For a point on the estimated surface
. For a point on the estimated surface 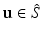 , we extract the oriented local image patch
, we extract the oriented local image patch 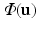 to create the appearance vector
to create the appearance vector 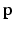 , and then compute the difference of the appearance model residuals from (3) such that
, and then compute the difference of the appearance model residuals from (3) such that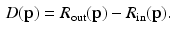
(4)
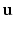 lies within the true boundary of the cortical surface in the CT image then
lies within the true boundary of the cortical surface in the CT image then 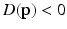 . Thus, the cortical surface boundary is located at the point
. Thus, the cortical surface boundary is located at the point 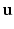 where
where 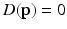 . We therefore seek the surface that minimizes the objective function
. We therefore seek the surface that minimizes the objective function