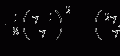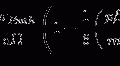(1)
Amersham, Buckinghamshire, UK
Abstract
The Gaussian and asymmetric collision energy loss pdfs that are derived in the following chapter arise from solutions to the two equations derived here. The form of the Chapman–Kolmogorov equation derived here is an integro-differential equation in the collision energy loss pdf 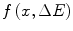 where
where 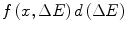 is the probability that a charged particle has lost kinetic energy between
is the probability that a charged particle has lost kinetic energy between 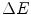 and
and 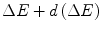 after penetrating to a depth x in a medium. The Bothe–Landau equation, also derived in this chapter, is a solution of the Chapman–Kolmogorov equation, and we will see in the following chapter how it can yield a Gaussian pdf of collision energy loss, provided a number of important assumptions are held. The asymmetric collision energy loss pdfs of Vavilov and Landau can be derived directly from the Chapman–Kolmogorov equation.
after penetrating to a depth x in a medium. The Bothe–Landau equation, also derived in this chapter, is a solution of the Chapman–Kolmogorov equation, and we will see in the following chapter how it can yield a Gaussian pdf of collision energy loss, provided a number of important assumptions are held. The asymmetric collision energy loss pdfs of Vavilov and Landau can be derived directly from the Chapman–Kolmogorov equation.
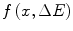 where
where 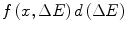 is the probability that a charged particle has lost kinetic energy between
is the probability that a charged particle has lost kinetic energy between 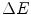 and
and 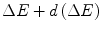 after penetrating to a depth x in a medium. The Bothe–Landau equation, also derived in this chapter, is a solution of the Chapman–Kolmogorov equation, and we will see in the following chapter how it can yield a Gaussian pdf of collision energy loss, provided a number of important assumptions are held. The asymmetric collision energy loss pdfs of Vavilov and Landau can be derived directly from the Chapman–Kolmogorov equation.
after penetrating to a depth x in a medium. The Bothe–Landau equation, also derived in this chapter, is a solution of the Chapman–Kolmogorov equation, and we will see in the following chapter how it can yield a Gaussian pdf of collision energy loss, provided a number of important assumptions are held. The asymmetric collision energy loss pdfs of Vavilov and Landau can be derived directly from the Chapman–Kolmogorov equation.17.1 Introductory Comments
In the last chapter, we began our study of energy loss straggling by deriving a simple descriptive numerical quantity, the straggling parameter, which is proportional to the variance of the energy loss pdf and the second moment of energy loss. Prior to that, in Part III, we derived the mean energy loss, through the collision stopping power, and which has been recast in the form of the stopping cross section throughout Part III and is also the first moment of energy loss.1 These two metrics are insufficient to fully characterise the pdf. In particular, the pdf does not necessarily have to be symmetric; in which case, the mean and most probable energy losses will not be equal. Hence, we must be capable of deriving the full pdf of energy loss which not only provides the mean and most probable energy losses and the variance of the distribution but also provides a complete description of the morphology of the pdf in a graphical representation as a function of ΔE.
Calculations of various energy loss pdfs describing the stochastic behaviour of collision energy loss are provided in the next chapter. The purpose of this chapter is to develop two tools that will prove useful, as will their variants, in the following chapter to derive charged particle energy loss pdfs. The loss of kinetic energy as a beam of charged particles penetrates into a medium is readily considered in terms of a continuity equation. The development of this provides us with the Chapman–Kolmogorov equation which is an integro-differential equation in the energy loss pdf 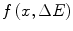 , where
, where 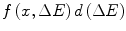 is the probability that a charged particle has lost kinetic energy between
is the probability that a charged particle has lost kinetic energy between 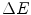 and
and 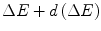 after penetrating to a depth x in a medium, and is based upon stochastic energy loss during penetration being a Markov process. This equation is derived here.
after penetrating to a depth x in a medium, and is based upon stochastic energy loss during penetration being a Markov process. This equation is derived here.
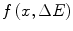 , where
, where 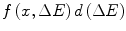 is the probability that a charged particle has lost kinetic energy between
is the probability that a charged particle has lost kinetic energy between 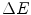 and
and 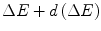 after penetrating to a depth x in a medium, and is based upon stochastic energy loss during penetration being a Markov process. This equation is derived here.
after penetrating to a depth x in a medium, and is based upon stochastic energy loss during penetration being a Markov process. This equation is derived here.Solutions to the Chapman–Kolmogorov equation are provided by the Bothe–Landau equation and its variants. Employing a number of simplifications, one converts the integro-differential form of the Chapman–Kolmogorov to a partial differential equation which can be solved using the Fourier or Laplace transform approaches. In this chapter, we derive a form of the Bothe–Landau equation (Bothe 1921; Landau 1944) using the Fourier transform (which will be shown in the next chapter to yield a Gaussian energy loss pdf provided certain assumptions are satisfied). Landau (1944) and Vavilov (1957) provided solutions to the Chapman–Kolmogorov equation, but discussion of these is deferred to that chapter.
17.2 Markov Process
A Markov process is a sequence of n statistically independent indexed events occurring such that the conditional probability of the random variable x n+1 being equal to the value j is dependent only upon the nth event. That is, the conditional probability of a future state given the current state is independent of any knowledge of all states prior to the nth event:
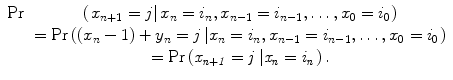
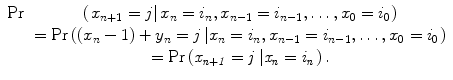
(17.1)
The process is a representation of the sequential energy losses that occur through uncorrelated projectile–atom collisions.
A practical example of a Markov process is that of standing in the rank at the airport awaiting a taxi. Assume that a taxi arrives at the stand once every a specified time interval. Let x n be the number of people awaiting a taxi at the start of the nth time interval and let y n be the number of people who join the queue at the taxi rank during the interval. Further, let us assume that the arrival of these customers occurs randomly with time. Hence,
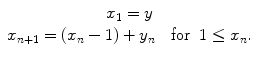
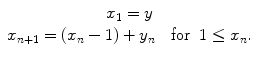
(17.2)
In addition, the number of people in the queue during the nth time interval is taken to be 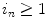 . Then, the conditional probability for the number of j people in the queue during the (n + 1)th time interval is
. Then, the conditional probability for the number of j people in the queue during the (n + 1)th time interval is
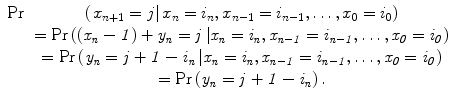
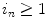 . Then, the conditional probability for the number of j people in the queue during the (n + 1)th time interval is
. Then, the conditional probability for the number of j people in the queue during the (n + 1)th time interval is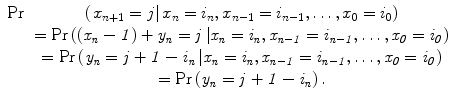
(17.3)
That is, the probability of y n being the number of people in the queue during the nth time interval is independent of the probabilities of the numbers of people being in the (n − 1)th time intervals and earlier. Hence, there is no dependence upon time or prior sequence. The Markov series in this context is considered as being time homogeneous. A compilation of a Markov series can be written in the form of an 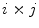 transition probability matrix:
transition probability matrix:
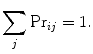
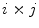 transition probability matrix:
transition probability matrix: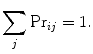
(17.5)
It subsequently follows that it is required that the sum of the matrix elements along each row be equal to the sum of total probabilities or
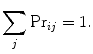
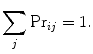
(17.6)
Now consider a chain of n statistically independent events which gives
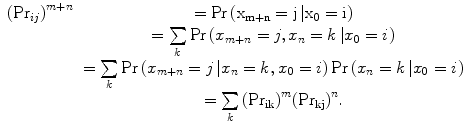
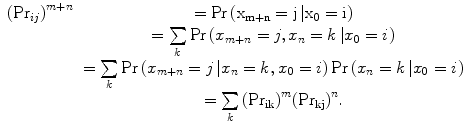
(17.7)
17.3 Chapman–Kolmogorov Equation
17.3.1 Definition
The Chapman–Kolmogorov equation relates joint probability distributions. On the basis of the above discussion of the Markov process, this equation follows in the discrete form:
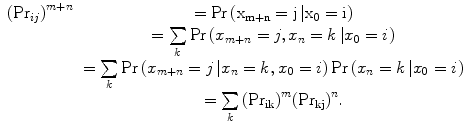
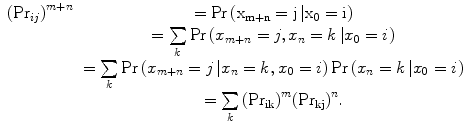
(17.8)
In a continuous form, if we define 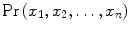 as the joint probability distribution of a collection of random variables
as the joint probability distribution of a collection of random variables 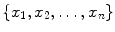 , the Chapman–Kolmogorov equation is
, the Chapman–Kolmogorov equation is
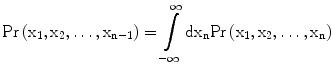
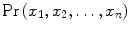 as the joint probability distribution of a collection of random variables
as the joint probability distribution of a collection of random variables 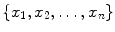 , the Chapman–Kolmogorov equation is
, the Chapman–Kolmogorov equation is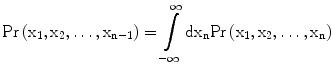
(17.9)
For example, from the Markov process of Sect. 17.2




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree