One naturally asks a question what is this density matrix and why do we need it. The answer is that the density matrix (DM) is a physical representation of an ensemble of atoms, molecules in a matrix format, whose elements tell us at any point in space and time what is the status of the spins and the spin system as a whole. In the absence of any external field the spins distribute themselves in a random manner in the brain. The net magnetism is thus zero. The magnitude of the magnetization (magnetic moment per unit volume) at any point in space and time is not constant in an ensemble like the brain. It is measured through the number of spins per unit volume N₀. One basically measures the susceptibility variation which is the same thing as the magnetization variation in space and time in the MRI mapping of the brain. The spin distribution overall can be assumed to be in equilibrium (though not uniform in space) in an ensemble like our brain. The equilibrium is due to the internal fields e.g. the magnetic fields of the nuclei, various metabolic activities etc.

In order to find about the behavior of the equilibrium and the associated activities (which basically what the MRI does) we first create a superficial equilibrium of our own by orienting all the spins (free and bound) along z-direction by a static magnetic field H_z. Then one uses RF radiation to interact with the ensemble i.e. the brain. In an ideal situation one would expect half of the population of spins would be along +z and the other half along –z direction. In a sense it is quite like tossing a coin and expecting that it would either be head or tail, since the probability for either (head or tail) is 1/2. But the real situation is quite different. There are many disturbances. We have temperature variations, spin interactions between electrons, atoms, etc., all over the brain. If you take a mole of the brain there are ~10²³ spins. But only a small fraction, p, of the 10²³ spins will be oriented along the field. Let us say there is a uniform background distribution of spin density (the number of spins per unit volume) over the brain. For simplicity it is convenient to call uniform density the background of spins as N ₀ and call the z-oriented ordered fractional concentration as p.

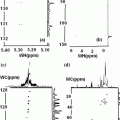
One can write the value of the ordered population at a temperature T as, p = N ₀ (ħγH _Z I _z )/(kT). Here γ is the overall average gyromagnetic ratio (note there are many species of nuclei, n_i, in the brain; one should take into account some kind of average of γ as γ = Σ_iγ_i/n_i). The other parameters in p are, ħ = the Planck’s constant, H_Z the static magnetic field, k = the Boltzmann constant and T = the temperature of the ensemble. It is more convenient to normalize p as a fraction between 0 and 1. So we take N₀ = 1 and remember that in the final result we have to multiply the result of p with N ₀ to get the absolute value of p. The p thus just represents a fractional number i.e. the ratio of the magnetic spin energy (ħγH_zI_z) with respect to the thermal energy kT. One can say p is the fraction of the spins contributing finally to the signal collected. I_z is the z-component of the spin with values (1/2)ħ and (−1/2)ħ. The reason why the matrix of the spin ensemble is called as the density matrix is clear now.

It gives the density of the population of spins in the various energy states and their evolution in time. It is possible to separate spins into sub-systems (groups) of 1-spin, 2-spin etc., by using magnetic field gradients in space and time in the brain. The density matrix of an ensemble is an arrangement of coefficients (representing fractions of spins) as elements in the matrix structure format. In its the simplest form a single-type spin ensemble (identical spins) is represented by a 2 × 2 density matrix. In the next level up i.e. in a 2-spin system by a 4 × 4 density matrix and so on. The density matrix has information about the time evolution of the spins and can be broken down into components along the y-axis along which direction the signal is measured. Without the application of the z-field the diagonal elements of the matrix under equilibrium (static magnetic field) have a uniform population density representation in up and down states of the spins. The net magnetization is thus zero.