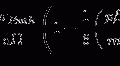(1)
Amersham, Buckinghamshire, UK
10.1.1 Organisation of Chapter
10.2.1 Massive Projectiles (m ≫ me)
10.5.1 Introductory Comments
10.5.2 Ionisation Energy Balance
10.5.3 Fowler Equation for W
10.5.4 Spencer–Fano Equation for W
Abstract
This chapter combines the soft- and hard-collision stopping powers derived in the two previous chapters to yield the total collision stopping power (but still not accounting for the higher-order effects to be studied in Chap. 12). For electron projectiles, we consider the restricted hard-collision stopping power derived in Chap. 9 to provide the restricted stopping power for electrons, a quantity of importance in practical radiation dosimetry evaluations. The main part of this chapter is, however, assigned to the theoretical investigation of the mean energy required to create an ion pair. This is a fundamental quantity not only to practical radiation dosimetry but also to our understanding of the ionisation resulting from the interaction of radiation with matter. We develop the generalised Fowler equation, which is essentially a transport equation, to yield the number of ion pairs created per unit energy transfer.
10.1 Introductory Comments
10.1.1 Organisation of Chapter
In this chapter, we cover three endpoints of much of our discussions of the soft- and hard-collision stopping powers in Chaps. 8 and 9. Further refinements remain and these are discussed in Chaps. 11, 12 and 14. The first is the combination of these to yield expressions for the complete collision stopping power. We then further discuss the practical matters of the stopping powers which are restricted in terms of kinetic energy transfer – a consideration of essential necessity in practical medical dosimetry. Finally, we consider the required energy expended to generate ionisation and how theory can guide us in its exploration.
Each component of this chapter is now introduced individually and in detail.
10.1.2 Total Collision Stopping Power
The total collision stopping power is, as expected, the summation of the soft-collision stopping power, which reflects energy transfer to the atom as a whole and investigated in Chap. 8, and the hard-collision stopping power, which is a result of the interaction between the projectile and an individual atomic electron. In Chap. 8, we explored the soft-collision stopping power in both classical (Bohr) and quantum (Bethe) theories. The former was based upon the use of the spatial impact parameter as the metric dividing between the regimes of soft and hard collisions. Contrary to this, the latter based the differentiation between soft and hard collisions upon momentum or energy transfer (i.e. 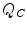 ) from the projectile to the atom. The latter is compatible with our approach of Chap. 9 in which hard collisions were considered solely through quantum-mechanical models. Hence, in this chapter, we will combine the foundation of the total collision stopping power through the summation of the Bethe soft-collision stopping power and the quantum-mechanical representations of the hard-collision stopping powers of Chap. 9.
) from the projectile to the atom. The latter is compatible with our approach of Chap. 9 in which hard collisions were considered solely through quantum-mechanical models. Hence, in this chapter, we will combine the foundation of the total collision stopping power through the summation of the Bethe soft-collision stopping power and the quantum-mechanical representations of the hard-collision stopping powers of Chap. 9.
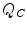 ) from the projectile to the atom. The latter is compatible with our approach of Chap. 9 in which hard collisions were considered solely through quantum-mechanical models. Hence, in this chapter, we will combine the foundation of the total collision stopping power through the summation of the Bethe soft-collision stopping power and the quantum-mechanical representations of the hard-collision stopping powers of Chap. 9.
) from the projectile to the atom. The latter is compatible with our approach of Chap. 9 in which hard collisions were considered solely through quantum-mechanical models. Hence, in this chapter, we will combine the foundation of the total collision stopping power through the summation of the Bethe soft-collision stopping power and the quantum-mechanical representations of the hard-collision stopping powers of Chap. 9.10.1.3 Restricted Collision Stopping Power
The absorbed dose is the ratio of the energy deposited by a charged particle within a volume within the medium to that volume (ICRU 1980). That energy frequently leads to ionisation, as will be discussed quantitatively in this chapter. The ionisation results in the generation of secondary electrons, i.e. atomic electrons ejected with kinetic energy and referred to as δ-rays. As these carry energy away from the interaction site, these do not contribute to the absorbed dose at the interaction site. Hence, for radiation dosimetry calculations, it is necessary to use the restricted collision stopping power which excludes those interactions that result in energy being transported at a distance from the interaction site. In this chapter, we will consider the restricted collision stopping power for electrons only.
10.1.4 Mean Energy Expended to Create an Ion Pair, W
The transfer of kinetic energy from a decelerating charged particle to atoms in the medium results in excitation and ionisation of the medium. Ionisation within tissue leads to disruptions in the cellular DNA which culminates in biological damage. Hence, the ability to calculate the ionisation yield for a given irradiation condition in order to estimate such effects is desirable. A metric for calculating this yield on the basis of energy lost by a charged particle is the mean energy expended to create an ion pair and which is denoted by W.
An important application of W results from the fact that absorbed dose calibrations in the clinical radiation setting are generally derived from measurements of the amount of ions (either in the form of collected charge or electric current) produced within a gas cavity within a medium. Consider, for example, a small volume of gas contained within an irradiated medium. Electrons traversing the medium create an absorbed dose, and the electron fluence traversing the cavity will create ionisations within the gas. Bragg–Gray cavity theory enables the determination of the absorbed dose from a measurement the collected electric charge in the gas,
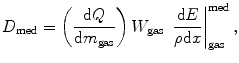
where 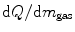 is the electric charge released through ionisations per unit mass within the cavity,1 W gas is the mean energy expended that for the gas and
is the electric charge released through ionisations per unit mass within the cavity,1 W gas is the mean energy expended that for the gas and 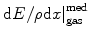 is the ratio of the mass collision stopping power of the medium for electrons to that of the gas.
is the ratio of the mass collision stopping power of the medium for electrons to that of the gas.
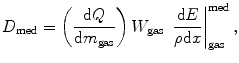
(10.1)
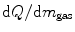 is the electric charge released through ionisations per unit mass within the cavity,1 W gas is the mean energy expended that for the gas and
is the electric charge released through ionisations per unit mass within the cavity,1 W gas is the mean energy expended that for the gas and 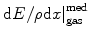 is the ratio of the mass collision stopping power of the medium for electrons to that of the gas.
is the ratio of the mass collision stopping power of the medium for electrons to that of the gas.10.2 Total Collision Stopping Power
10.2.1 Massive Projectiles (m ≫ me)
Neglecting spin, the Bethe total mass collision stopping power is given by the sum of the Bethe soft mass collision power expression of (8.344) and the hard mass collision stopping power of a massive spin-0 projectile from (9.7):
![$$ \begin{array}{cclclclcllc} \frac{{{\rm d}E}}{{\rho {\rm d}x}}&= {{\left. {\frac{{{\rm d}E}}{{\rho {\rm d}x}}} \right|}_S}+{{\left. {\frac{{{\rm d}E}}{{\rho {\rm d}x}}} \right|}_H} \\&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{Q_{\rm C}}}}{{{{\bar{I}}^2}}}{\beta^2}} \right)-\ln \left( {1-{\beta^2}} \right)-{\beta^2}+\ln \left( {\frac{{{Q_{\max }}}}{{{Q_C}}}} \right)-{\beta^2}} \right] \\&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{Q_{\max }}}}{{{{\bar{I}}^2}}}{\beta^2}} \right)-\ln \left( {1-{\beta^2}} \right)-2{\beta^2}} \right].\end{array} $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00102.gif)
![$$ \begin{array}{cclclclcllc} \frac{{{\rm d}E}}{{\rho {\rm d}x}}&= {{\left. {\frac{{{\rm d}E}}{{\rho {\rm d}x}}} \right|}_S}+{{\left. {\frac{{{\rm d}E}}{{\rho {\rm d}x}}} \right|}_H} \\&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{Q_{\rm C}}}}{{{{\bar{I}}^2}}}{\beta^2}} \right)-\ln \left( {1-{\beta^2}} \right)-{\beta^2}+\ln \left( {\frac{{{Q_{\max }}}}{{{Q_C}}}} \right)-{\beta^2}} \right] \\&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{Q_{\max }}}}{{{{\bar{I}}^2}}}{\beta^2}} \right)-\ln \left( {1-{\beta^2}} \right)-2{\beta^2}} \right].\end{array} $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00102.gif)
(10.2)
As desired, the Q C factors in the logarithmic terms of the soft- and hard-collision stopping powers cancel. As noted before, the maximum energy transfer to an electron for the case of a heavy projectile (i.e. one with mass 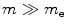 ) is
) is 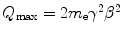 . Inserting this gives the complete mass collision stopping power for a massive spin-0 projectile:
. Inserting this gives the complete mass collision stopping power for a massive spin-0 projectile:
![$$ \begin{array}{cclclclcllc} \frac{{{\rm d}E}}{{\rho { d}x}}&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{Q_{\max }}}}{{{{\bar{I}}^2}}}{\beta^2}} \right)-\ln \left( {1-{\beta^2}} \right)-2{\beta^2}} \right] \\&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{4m_{\mathrm{ e}}^2}}{{{{\bar{I}}^2}}}{\beta^2}} \right)-2\ln \left( {1-{\beta^2}} \right)-2{\beta^2}} \right] \\&= 2C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}}}{\bar{I}}\beta } \right)-\ln \left( {1-{\beta^2}} \right)-{\beta^2}} \right] \\& \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \mathrm{ Spin}\text{--}0\end{array} $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00103.gif)
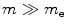 ) is
) is 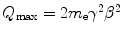 . Inserting this gives the complete mass collision stopping power for a massive spin-0 projectile:
. Inserting this gives the complete mass collision stopping power for a massive spin-0 projectile:![$$ \begin{array}{cclclclcllc} \frac{{{\rm d}E}}{{\rho { d}x}}&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{Q_{\max }}}}{{{{\bar{I}}^2}}}{\beta^2}} \right)-\ln \left( {1-{\beta^2}} \right)-2{\beta^2}} \right] \\&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{4m_{\mathrm{ e}}^2}}{{{{\bar{I}}^2}}}{\beta^2}} \right)-2\ln \left( {1-{\beta^2}} \right)-2{\beta^2}} \right] \\&= 2C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}}}{\bar{I}}\beta } \right)-\ln \left( {1-{\beta^2}} \right)-{\beta^2}} \right] \\& \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \mathrm{ Spin}\text{--}0\end{array} $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00103.gif)
(10.3)
Similarly, the total mass collision stopping power or a massive spin-½ projectile is given by the sum of (8.344) and (9.2):
![$$ \begin{array}{cclclclcllc} \frac{{{ d}E}}{{\rho { d}x}}&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{Q_{\rm C}}}}{{{{\bar{I}}^2}}}{\beta^2}} \right)-\ln \left( {1-{\beta^2}} \right)-{\beta^2}} \right. \\& \;\quad+\left. {\ln \left( {\frac{{{Q_{\max }}}}{{{Q_{\rm C}}}}} \right)-{\beta^2}+{{{\left( {\frac{{{Q_{\max }}}}{{2\left( {E+m} \right)}}} \right)}}{^2}}} \right] \\&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left( {\ln \left( {\frac{{4m_{\mathrm{ e}}^2}}{{{{\bar{I}}^2}}}{\beta^2}} \right)-2\ln \left( {1-{\beta^2}} \right)-2{\beta^2}+{{{\left( {\frac{{{Q_{\max }}}}{{2\left( {E+m} \right)}}} \right)}}{^2}}} \right) \\&= 2C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left( {\ln \left( {\frac{{2{m_{\mathrm{ e}}}}}{\bar{I}}\beta } \right)-\ln \left( {1-{\beta^2}} \right)-{\beta^2}+\frac{1}{8}{{{\left( {\frac{{{Q_{\max }}}}{{\left( {E+m} \right)}}} \right)}}{^2}}} \right) \\&= 2C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left( {\ln \left( {\frac{{2{m_{\mathrm{ e}}}}}{\bar{I}}\beta } \right)-\ln \left( {1-{\beta^2}} \right)-{\beta^2}+\frac{1}{2}{{{\left( {\frac{{{m_{\mathrm{ e}}}}}{{\left( {E+m} \right)}}\frac{{{\beta^2}}}{{\left( {1-{\beta^2}} \right)}}} \right)}}{^2}}} \;\right). \\& \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \mathrm{ Spin}{1} {2}\end{array} $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00104.gif)
![$$ \begin{array}{cclclclcllc} \frac{{{ d}E}}{{\rho { d}x}}&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{Q_{\rm C}}}}{{{{\bar{I}}^2}}}{\beta^2}} \right)-\ln \left( {1-{\beta^2}} \right)-{\beta^2}} \right. \\& \;\quad+\left. {\ln \left( {\frac{{{Q_{\max }}}}{{{Q_{\rm C}}}}} \right)-{\beta^2}+{{{\left( {\frac{{{Q_{\max }}}}{{2\left( {E+m} \right)}}} \right)}}{^2}}} \right] \\&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left( {\ln \left( {\frac{{4m_{\mathrm{ e}}^2}}{{{{\bar{I}}^2}}}{\beta^2}} \right)-2\ln \left( {1-{\beta^2}} \right)-2{\beta^2}+{{{\left( {\frac{{{Q_{\max }}}}{{2\left( {E+m} \right)}}} \right)}}{^2}}} \right) \\&= 2C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left( {\ln \left( {\frac{{2{m_{\mathrm{ e}}}}}{\bar{I}}\beta } \right)-\ln \left( {1-{\beta^2}} \right)-{\beta^2}+\frac{1}{8}{{{\left( {\frac{{{Q_{\max }}}}{{\left( {E+m} \right)}}} \right)}}{^2}}} \right) \\&= 2C\left( {\frac{Z}{A}} \right){{\left( {\frac{z}{\beta }} \right)}^2}\left( {\ln \left( {\frac{{2{m_{\mathrm{ e}}}}}{\bar{I}}\beta } \right)-\ln \left( {1-{\beta^2}} \right)-{\beta^2}+\frac{1}{2}{{{\left( {\frac{{{m_{\mathrm{ e}}}}}{{\left( {E+m} \right)}}\frac{{{\beta^2}}}{{\left( {1-{\beta^2}} \right)}}} \right)}}{^2}}} \;\right). \\& \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \mathrm{ Spin}{1} {2}\end{array} $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00104.gif)
(10.4)
As m ≫ m e, it is clear that the mass collision stopping power for a massive spin-½ projectile rapidly reduces to that for a spin-0 projectile at low kinetic energies (i.e.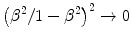 ).
).
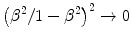 ).
).For the following quantitative consideration of the total collision stopping power, we will replace our usual high-Z elemental medium of calcium with that of lead. The reason for doing so shall become apparent. Figure 10.1 shows the mass collision stopping power calculated for a proton in carbon and lead as a function of the proton’s kinetic energy. The two extremes in terms of atomic number are deliberately selected for a reason to be demonstrated shortly. Both curves of 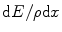 exhibit the same characteristic behaviour of a decrease with increasing kinetic energy, due to the
exhibit the same characteristic behaviour of a decrease with increasing kinetic energy, due to the 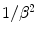 factor, to a broad minimum of about 1–2 MeV cm2/g which occurs at a particle kinetic energy equal to about three times its rest mass. This is referred to as the minimally ionising region. With increasing kinetic energy, the mass collision stopping power increases logarithmically at large β due to the
factor, to a broad minimum of about 1–2 MeV cm2/g which occurs at a particle kinetic energy equal to about three times its rest mass. This is referred to as the minimally ionising region. With increasing kinetic energy, the mass collision stopping power increases logarithmically at large β due to the 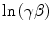 term. This increase could be quenched, however, in condensed media due to polarisation, as discussed in Chap. 12. It will be noted from Fig. 10.1 that for a given projectile kinetic energy, the mass collision stopping power for carbon (Z = 6) is greater than that for lead (Z = 82). This is a result of the combined facts of the energy loss being dominated by interactions with atomic electrons over those with the nucleus and the electron density being proportional to
term. This increase could be quenched, however, in condensed media due to polarisation, as discussed in Chap. 12. It will be noted from Fig. 10.1 that for a given projectile kinetic energy, the mass collision stopping power for carbon (Z = 6) is greater than that for lead (Z = 82). This is a result of the combined facts of the energy loss being dominated by interactions with atomic electrons over those with the nucleus and the electron density being proportional to 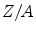 . As a result, the ratio of the carbon to lead mass collision stopping powers is (excluding the effect of the mean excitation energy which is limited due to its placement within the logarithm)
. As a result, the ratio of the carbon to lead mass collision stopping powers is (excluding the effect of the mean excitation energy which is limited due to its placement within the logarithm)
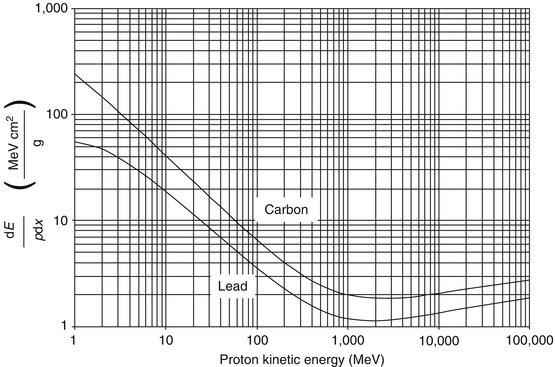
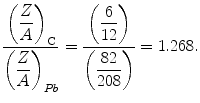
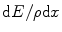 exhibit the same characteristic behaviour of a decrease with increasing kinetic energy, due to the
exhibit the same characteristic behaviour of a decrease with increasing kinetic energy, due to the 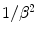 factor, to a broad minimum of about 1–2 MeV cm2/g which occurs at a particle kinetic energy equal to about three times its rest mass. This is referred to as the minimally ionising region. With increasing kinetic energy, the mass collision stopping power increases logarithmically at large β due to the
factor, to a broad minimum of about 1–2 MeV cm2/g which occurs at a particle kinetic energy equal to about three times its rest mass. This is referred to as the minimally ionising region. With increasing kinetic energy, the mass collision stopping power increases logarithmically at large β due to the 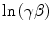 term. This increase could be quenched, however, in condensed media due to polarisation, as discussed in Chap. 12. It will be noted from Fig. 10.1 that for a given projectile kinetic energy, the mass collision stopping power for carbon (Z = 6) is greater than that for lead (Z = 82). This is a result of the combined facts of the energy loss being dominated by interactions with atomic electrons over those with the nucleus and the electron density being proportional to
term. This increase could be quenched, however, in condensed media due to polarisation, as discussed in Chap. 12. It will be noted from Fig. 10.1 that for a given projectile kinetic energy, the mass collision stopping power for carbon (Z = 6) is greater than that for lead (Z = 82). This is a result of the combined facts of the energy loss being dominated by interactions with atomic electrons over those with the nucleus and the electron density being proportional to 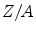 . As a result, the ratio of the carbon to lead mass collision stopping powers is (excluding the effect of the mean excitation energy which is limited due to its placement within the logarithm)
. As a result, the ratio of the carbon to lead mass collision stopping powers is (excluding the effect of the mean excitation energy which is limited due to its placement within the logarithm)
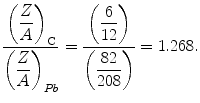
In other words, the mass collision stopping power for carbon is greater than that for lead due to the greater number of electrons per unit mass.
10.2.2 Electron and Positron Projectiles
To obtain the unrestricted mass collision stopping power of an electron projectile, we sum the Bethe mass soft-collision stopping power (8.344) and the Møller mass hard-collision stopping power (9.10):
![$$ \begin{array}{cclclclcllc} {{\left. {\frac{{{\rm d}E}}{{\rho { d}x}}} \right|}_{{{e^{-}}}}}&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{1}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{Q_{\rm C}}}}{{{{\bar{I}}^2}}}{\gamma^2}{\beta^2}} \right)-{\beta^2}+\ln \left( {\frac{E}{{4{Q_{\rm C}}}}} \right)} \right. \\&\quad\; \left. {+1+\frac{1}{8}{{{\left( {\frac{{\gamma -1}}{\gamma }} \right)}}^2}-\left( {\frac{{2\gamma -1}}{{{\gamma^2}}}} \right)\ln 2} \right] \\&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{1}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{{m_{\mathrm{ e}}}E}}{{2{{\bar{I}}^2}}}{\gamma^2}{\beta^2}} \right)+{f^{-}}\left( \gamma \right)} \right]\end{array} $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00105.gif)
where E is the electron kinetic energy and the parameter
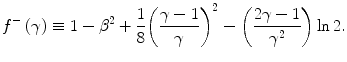
![$$ \begin{array}{cclclclcllc} {{\left. {\frac{{{\rm d}E}}{{\rho { d}x}}} \right|}_{{{e^{-}}}}}&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{1}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{Q_{\rm C}}}}{{{{\bar{I}}^2}}}{\gamma^2}{\beta^2}} \right)-{\beta^2}+\ln \left( {\frac{E}{{4{Q_{\rm C}}}}} \right)} \right. \\&\quad\; \left. {+1+\frac{1}{8}{{{\left( {\frac{{\gamma -1}}{\gamma }} \right)}}^2}-\left( {\frac{{2\gamma -1}}{{{\gamma^2}}}} \right)\ln 2} \right] \\&= C\left( {\frac{Z}{A}} \right){{\left( {\frac{1}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{{m_{\mathrm{ e}}}E}}{{2{{\bar{I}}^2}}}{\gamma^2}{\beta^2}} \right)+{f^{-}}\left( \gamma \right)} \right]\end{array} $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00105.gif)
(10.5)
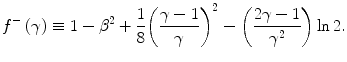
(10.6)
By using the relativistic relationship,
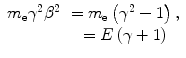 the (unrestricted) electron mass hard-collision stopping power is simplified to
the (unrestricted) electron mass hard-collision stopping power is simplified to
![$$ {{\left. {\frac{{{\rm d}E}}{{\rho { d}x}}} \right|}_{{{e^{-}}}}}=C\left( {\frac{Z}{A}} \right){{\left( {\frac{1}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{{E^2}\left( {\gamma +1} \right)}}{{2{{\bar{I}}^2}}}} \right)+{f^{-}}\left( \gamma \right)} \right]. $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00107.gif)
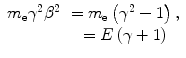
![$$ {{\left. {\frac{{{\rm d}E}}{{\rho { d}x}}} \right|}_{{{e^{-}}}}}=C\left( {\frac{Z}{A}} \right){{\left( {\frac{1}{\beta }} \right)}^2}\left[ {\ln \left( {\frac{{{E^2}\left( {\gamma +1} \right)}}{{2{{\bar{I}}^2}}}} \right)+{f^{-}}\left( \gamma \right)} \right]. $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00107.gif)
(10.7)
Similarly, to obtain the positron complete collision stopping power, we add the Bethe mass soft- and the Bhabha mass hard-collision stopping powers:
![$$ {{\left. {\frac{{{\rm d}E}}{{\rho { d}x}}} \right|}_{{{e^{+}}}}}=C\left( {\frac{Z}{A}} \right)\frac{1}{{{\beta^2}}}\left[ {\ln \left( {\frac{{{E^2}\left( {\gamma +1} \right)}}{{2{{\bar{I}}^2}}}} \right)+{f^{+}}\left( \gamma \right)} \right] $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00108.gif)
where
![$$ {f^{+}}\left( \gamma \right)=2\ln 2-\frac{{{\beta^2}}}{12}\left[ {23+\frac{14 }{{\left( {\gamma +1} \right)}}+\frac{10 }{{{{{\left( {\gamma +1} \right)}}^2}}}+\frac{4}{{{{{\left( {\gamma +1} \right)}}^3}}}} \right]. $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00109.gif)
![$$ {{\left. {\frac{{{\rm d}E}}{{\rho { d}x}}} \right|}_{{{e^{+}}}}}=C\left( {\frac{Z}{A}} \right)\frac{1}{{{\beta^2}}}\left[ {\ln \left( {\frac{{{E^2}\left( {\gamma +1} \right)}}{{2{{\bar{I}}^2}}}} \right)+{f^{+}}\left( \gamma \right)} \right] $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00108.gif)
(10.8)
![$$ {f^{+}}\left( \gamma \right)=2\ln 2-\frac{{{\beta^2}}}{12}\left[ {23+\frac{14 }{{\left( {\gamma +1} \right)}}+\frac{10 }{{{{{\left( {\gamma +1} \right)}}^2}}}+\frac{4}{{{{{\left( {\gamma +1} \right)}}^3}}}} \right]. $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ00109.gif)
(10.9)
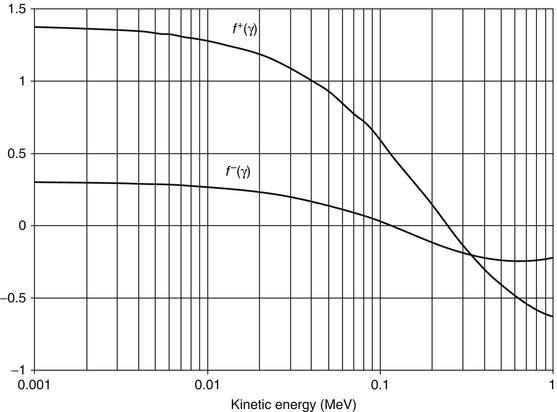
A comparison of these electron and positron mass collision stopping powers shows that the difference between the electron and positron mass collisions stopping powers resides within the difference between 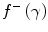 and
and 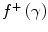 . These two terms are plotted in Fig. 10.2 as functions of the kinetic energy of the incident electron/positron (only the unrestricted version of
. These two terms are plotted in Fig. 10.2 as functions of the kinetic energy of the incident electron/positron (only the unrestricted version of 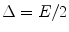 is used for the electron term). At low energies,
is used for the electron term). At low energies, 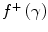 exceeds
exceeds 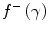 by about a factor of 3 and decreases with positron kinetic energy to equal
by about a factor of 3 and decreases with positron kinetic energy to equal 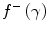 at about 0.32 MeV. Note that both
at about 0.32 MeV. Note that both 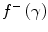 and
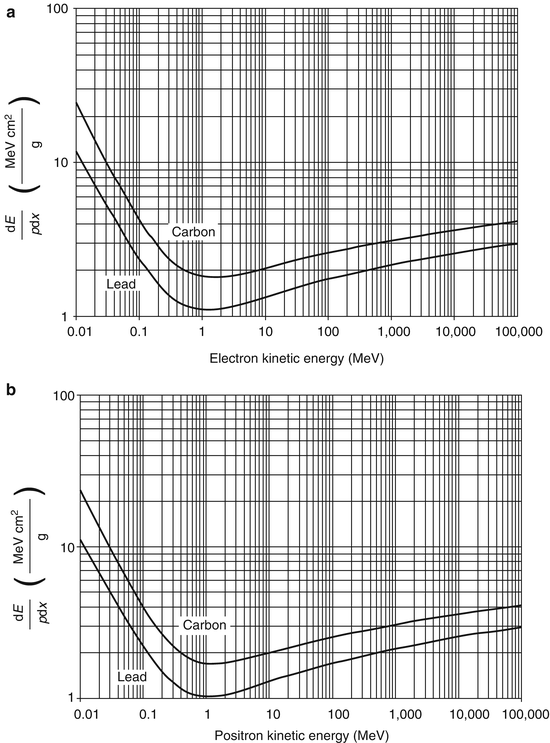
and 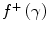 become negative with increasing kinetic energy. However, when we compare the electron and positron unrestricted mass collision stopping powers for carbon and lead shown in Fig. 10.3, we see that there is little difference between the two which reflects the dominance of the logarithmic term in the collision stopping power expression over the magnitudes of
become negative with increasing kinetic energy. However, when we compare the electron and positron unrestricted mass collision stopping powers for carbon and lead shown in Fig. 10.3, we see that there is little difference between the two which reflects the dominance of the logarithmic term in the collision stopping power expression over the magnitudes of 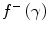 and
and 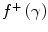 . The mass collision stopping power curves exhibit the same characteristics as those derived earlier for the proton. A clear comparison of the curves shows that while the mass collision stopping power of protons, electrons and positrons are roughly equal in the minimally ionising region, the kinetic energy at which this region occurs is equal to roughly equal to three times the particle rest mass (3 GeV for protons and 1.5 MeV for electrons and positrons) or for a speed of the order of β ≈ 0.8.
. The mass collision stopping power curves exhibit the same characteristics as those derived earlier for the proton. A clear comparison of the curves shows that while the mass collision stopping power of protons, electrons and positrons are roughly equal in the minimally ionising region, the kinetic energy at which this region occurs is equal to roughly equal to three times the particle rest mass (3 GeV for protons and 1.5 MeV for electrons and positrons) or for a speed of the order of β ≈ 0.8.
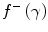 and
and 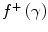 . These two terms are plotted in Fig. 10.2 as functions of the kinetic energy of the incident electron/positron (only the unrestricted version of
. These two terms are plotted in Fig. 10.2 as functions of the kinetic energy of the incident electron/positron (only the unrestricted version of 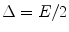 is used for the electron term). At low energies,
is used for the electron term). At low energies, 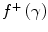 exceeds
exceeds 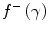 by about a factor of 3 and decreases with positron kinetic energy to equal
by about a factor of 3 and decreases with positron kinetic energy to equal 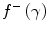 at about 0.32 MeV. Note that both
at about 0.32 MeV. Note that both 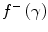 and
and 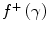 become negative with increasing kinetic energy. However, when we compare the electron and positron unrestricted mass collision stopping powers for carbon and lead shown in Fig. 10.3, we see that there is little difference between the two which reflects the dominance of the logarithmic term in the collision stopping power expression over the magnitudes of
become negative with increasing kinetic energy. However, when we compare the electron and positron unrestricted mass collision stopping powers for carbon and lead shown in Fig. 10.3, we see that there is little difference between the two which reflects the dominance of the logarithmic term in the collision stopping power expression over the magnitudes of 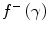 and
and 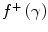 . The mass collision stopping power curves exhibit the same characteristics as those derived earlier for the proton. A clear comparison of the curves shows that while the mass collision stopping power of protons, electrons and positrons are roughly equal in the minimally ionising region, the kinetic energy at which this region occurs is equal to roughly equal to three times the particle rest mass (3 GeV for protons and 1.5 MeV for electrons and positrons) or for a speed of the order of β ≈ 0.8.
. The mass collision stopping power curves exhibit the same characteristics as those derived earlier for the proton. A clear comparison of the curves shows that while the mass collision stopping power of protons, electrons and positrons are roughly equal in the minimally ionising region, the kinetic energy at which this region occurs is equal to roughly equal to three times the particle rest mass (3 GeV for protons and 1.5 MeV for electrons and positrons) or for a speed of the order of β ≈ 0.8.
Fig. 10.2
The functions f –(γ) and f +(γ) of the mass collision stopping powers of electrons and positrons, respectively, as a function of the kinetic energy of the electron or positron
10.3 Restricted Collision Stopping Power
An important refinement in the definition of the collision stopping power is the introduction of the restricted collision stopping power. Recall that the collision stopping power describes the mean rate of energy transfer from the charged projectile to the medium through both soft and hard collisions. This energy transfer can ionise an atom with the result that the ejected electron can carry considerable kinetic energy away a significant distance from the interaction site. The calculation of the energy deposition in a small volume using the mass collision stopping power will thus overestimate the amount of energy deposited within that. To correct for this, the restricted stopping power contains the sum of the soft-collision energy transfers and the energy transferred in hard collisions which result in δ-rays with kinetic energies which are less than a specified cut-off energy, Δ.
For example, the electron-restricted mass collision stopping power is
![$$ \begin{array}{cclclclcllc} {{\left. {\frac{{{\rm d}E}}{{\rho { d}x}}} \right|}_{{\Delta, {{\mathrm{ e}}^{-}}}}}&={{\left. {\frac{{{\rm d}E}}{{\rho { d}x}}} \right|}_{{S,{{\mathrm{ e}}^{-}}}}}+{{\left. {\frac{{{\rm d}E}}{{\rho { d}x}}} \right|}_{{H,\Delta, {{\mathrm{ e}}^{-}}}}} \\&=\displaystyle C\left( {\frac{Z}{A}} \right){{{\left( {\frac{1}{\beta }} \right)}}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{Q_{\rm C}}}}{{{{\bar{I}}^2}}}{\gamma^2}{\beta^2}} \right)-{\beta^2}+\ln \left( {\frac{{\Delta \left( {1-\displaystyle\frac{\Delta}{E}} \right)}}{{{Q_C}}}} \right)} \right. \\ {\left. { \displaystyle +\left( {\frac{1}{{1-\left( {\frac{\Delta}{E}} \right)}}-1} \right)+{{{\left( {\frac{{\gamma -1}}{\gamma }} \right)}}^2}\frac{{{\Delta^2}}}{{2{E^2}}}+\left( {\frac{{2\gamma -1}}{\gamma }} \right)\ln \left( {1-\frac{\Delta}{E}} \right)} \right]} \\& =C\left( {\frac{Z}{A}} \right){{\left( {\frac{1}{\beta }} \right)}^2}\left( {\ln \left( {\frac{{2\Delta \left( {E-\Delta} \right)}}{{{{\overline{I}}^2}}}\left( {\gamma +1} \right)} \right)+{f^{-}}\left( {\gamma, \Delta} \right)} \right)\end{array} $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ001010.gif)
where
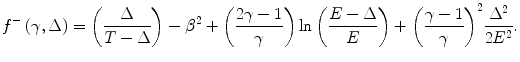
![$$ \begin{array}{cclclclcllc} {{\left. {\frac{{{\rm d}E}}{{\rho { d}x}}} \right|}_{{\Delta, {{\mathrm{ e}}^{-}}}}}&={{\left. {\frac{{{\rm d}E}}{{\rho { d}x}}} \right|}_{{S,{{\mathrm{ e}}^{-}}}}}+{{\left. {\frac{{{\rm d}E}}{{\rho { d}x}}} \right|}_{{H,\Delta, {{\mathrm{ e}}^{-}}}}} \\&=\displaystyle C\left( {\frac{Z}{A}} \right){{{\left( {\frac{1}{\beta }} \right)}}^2}\left[ {\ln \left( {\frac{{2{m_{\mathrm{ e}}}{Q_{\rm C}}}}{{{{\bar{I}}^2}}}{\gamma^2}{\beta^2}} \right)-{\beta^2}+\ln \left( {\frac{{\Delta \left( {1-\displaystyle\frac{\Delta}{E}} \right)}}{{{Q_C}}}} \right)} \right. \\ {\left. { \displaystyle +\left( {\frac{1}{{1-\left( {\frac{\Delta}{E}} \right)}}-1} \right)+{{{\left( {\frac{{\gamma -1}}{\gamma }} \right)}}^2}\frac{{{\Delta^2}}}{{2{E^2}}}+\left( {\frac{{2\gamma -1}}{\gamma }} \right)\ln \left( {1-\frac{\Delta}{E}} \right)} \right]} \\& =C\left( {\frac{Z}{A}} \right){{\left( {\frac{1}{\beta }} \right)}^2}\left( {\ln \left( {\frac{{2\Delta \left( {E-\Delta} \right)}}{{{{\overline{I}}^2}}}\left( {\gamma +1} \right)} \right)+{f^{-}}\left( {\gamma, \Delta} \right)} \right)\end{array} $$](/wp-content/uploads/2016/04/A306762_1_En_10_Chapter_Equ001010.gif)
(10.10)
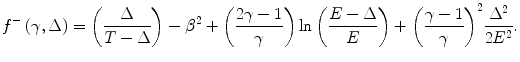
(10.11)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree