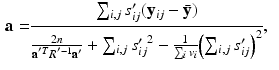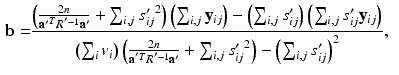Trajectory and Progression Score Estimation from Voxelwise Longitudinal Imaging Measures: Application to Amyloid Imaging

-amyloid deposition begins in Alzheimer’s disease (AD) years before the onset of any clinical symptoms. It is therefore important to determine the temporal trajectories of amyloid deposition in these earliest stages in order to better understand their associations with progression to AD. A method for estimating the temporal trajectories of voxelwise amyloid as measured using longitudinal positron emission tomography (PET) imaging is presented. The method involves the estimation of a score for each subject visit based on the PET data that reflects their amyloid progression. This amyloid progression score allows subjects with similar progressions to be aligned and analyzed together. The estimation of the progression scores and the amyloid trajectory parameters are performed using an expectation-maximization algorithm. The correlations among the voxel measures of amyloid are modeled to reflect the spatial nature of PET images. Simulation results show that model parameters are captured well at a variety of noise and spatial correlation levels. The method is applied to longitudinal amyloid imaging data considering each cerebral hemisphere separately. The results are consistent across the hemispheres and agree with a global index of brain amyloid known as mean cortical DVR. Unlike mean cortical DVR, which depends on a priori defined regions, the progression score extracted by the method is data-driven and does not make assumptions about regional longitudinal changes. Compared to regressing on age at each voxel, the longitudinal trajectory slopes estimated using the proposed method show better localized longitudinal changes.

Keywords

Progression scoreAmyloidPittsburgh compound BPiBLongitudinal image analysis

1 Introduction

Cortical $\beta$ -amyloid deposition is a neuropathological hallmark associated with Alzheimer’s disease (AD), and begins years before any cognitive symptoms of AD are evident [8]. Studying within-subject longitudinal changes is limited by the number of follow-up visits. The relatively short span of longitudinal positron emission tomograpy (PET) studies of amyloid deposition compared to its hypothesized timeline makes it difficult to extensively study the longitudinal brain amyloid changes that occur in the preclinical stages of AD.

It is possible to “stitch” data across subjects in order to obtain temporal biomarker trajectories that fit an underlying model. This is the premise of the Disease Progression Score method, which has been applied to studying changes in cognitive and biological markers related to Alzheimer’s disease [3, 9]. It is assumed that there is an underlying progression score (PS) for each subject visit that is a linear transform of the subject’s age, and given this PS, it is possible to place biomarker measurements across a group of subjects onto a common timeline. The linear transformation of age removes across-subject variability in baseline biomarker measures as well as in their rates of longitudinal progression. Each biomarker is associated with a parametric trajectory as a function of PS, whose parameters are estimated along with the PS for each subject.

Other methods for analyzing trajectories of biomarkers have been proposed. One approach involves fitting a piecewise linear model to longitudinal data assuming that each biomarker becomes abnormal a certain number of years before clinical diagnosis, and this duration is estimated for each biomarker to yield the longitudinal trajectories as a function of time to diagnosis [13]. In another approach, an event-based probabilistic framework is used to determine the ordering of changes in longitudinal biomarker measures as well as the appropriate thresholds for separating normal from abnormal measures [14]. The second method is agnostic to clinical diagnosis, but does not allow for the characterization of longitudinal biomarker trajectories except for determining the ordering of the change points. The first method does delineate the longitudinal trajectories for each biomarker, but requires knowledge of clinical diagnosis and therefore is not suitable for studying the earliest changes in healthy individuals.

Here, we adopt the disease progression score principle, but make two substantial innovations. First, the voxelwise PET measures constitute the biomarkers in the model. Since voxelwise PET measures have an underlying spatial correlation, we incorporate the modeling of the spatial correlations among the biomarker error terms and estimate the spatial correlations along with the subject and trajectory parameters. Modeling spatial correlations makes the inference of the subject-specific progression scores less susceptible to the inherent correlations among the voxels. Second, instead of using an alternating least-squares approach for parameter estimation, we formulate the model fitting as an expectation-maximization (EM) algorithm, which guarantees optimality and convergence. In experiments using this approach, we first show using simulated data that the model parameters are estimated accurately, then apply the method to each cerebral hemisphere separately using distribution volume ratio (DVR) images derived from Pittsburgh compound B (PiB) PET imaging, which show the distribution of amyloid. Models fitted using data for 75 participants with a total of 271 visits reveal that the precuneus and frontal lobes show the greatest longitudinal increases in amyloid, with smaller increases in lateral temporal and temporoparietal regions, and minimal increases in the occipital lobe and the sensorimotor strip. Results are consistent across the two hemispheres, and the estimated PS agrees with a widely used global index of brain amyloid known as mean cortical DVR.

2 Method

2.1 Model

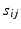The progression score $s_{ij}$ for subject i at visit j is assumed to be a linear transformation of age $t_{ij}$ :

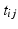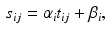
$\begin{aligned} s_{ij} = \alpha _i t_{ij} + \beta _i, \end{aligned}$

(1)

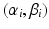where $(\alpha _i, \beta _i)$ are assumed to be uniformly distributed random variables on a fixed and large domain 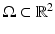$\Omega \subset \mathbb {R}^2$ . The collection of K biomarker measurements (the intensities at each PiB-PET DVR voxel reflecting amyloid levels) make up the 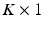$K \times 1$ vector 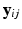$\mathbf {y}_{ij}$ . The longitudinal trajectories associated with these biomarkers are assumed have a linear form parameterized by 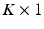$K \times 1$ vectors $\mathbf {a} = [a_1, a_2, \ldots , a_K]^T$ and $\mathbf {b} = [b_1, \ldots , b_K]^T$ :

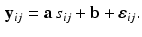
$\begin{aligned} \mathbf {y}_{ij} = \mathbf {a} \, s_{ij} + \mathbf {b} + \varvec{\varepsilon }_{ij}. \end{aligned}$

(2)

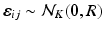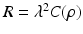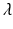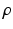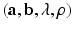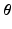Here, $\varvec{\varepsilon }_{ij} \sim \mathcal {N}_K(\mathbf {0},R)$ is the observation noise. The covariance matrix R is assumed to be of the form $R = \lambda ^2 C(\rho )$ , where $\lambda$ is a positive scalar and C is a correlation matrix parameterized by $\rho$ . The parameters $(\mathbf {a}, \mathbf {b}, \lambda , \rho )$ make up $\varvec{\theta }$ .

2.2 Log-Likelihood Function

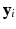Let $\mathbf {y}_i$ be the vector consisting of all biomarker measurements stacked across all visits of subject i and let $\mathbf {u}_i = [\alpha _i, \beta _i]^T$ . We then define $\mathbf {y} = \left[ \mathbf {y}^T_1, \mathbf {y}^T_2, \ldots , \mathbf {y}^T_n\right] ^T$ and $\mathbf {u} = \left[ \mathbf {u}^T_1, \mathbf {u}^T_2, \ldots , \mathbf {u}^T_n\right] ^T$ , where n is the number of subjects. 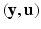The pair $(\mathbf {y}, \mathbf {u})$ is the complete data. The complete log-likelihood for the model, ignoring the constants, is given by

$\begin{aligned} \ell (\mathbf {y}, \mathbf {u} \mid \varvec{\theta })= & {} -\sum _{i,j} \left[ \log (\det \, R ) + \left( \mathbf {y}_{ij} - Z_{ij} \mathbf {u}_i - \mathbf {b} \right) ^T R^{-1} \left( \mathbf {y}_{ij} - Z_{ij} \mathbf {u}_i - \mathbf {b} \right) \right] , \; \; \; \; \end{aligned}$

(3)

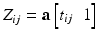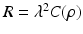where $Z_{ij} = \mathbf {a} \begin{bmatrix} t_{ij}&1 \end{bmatrix}$ and $R = \lambda ^2 C(\rho )$ .

2.3 EM Algorithm Derivation

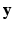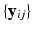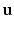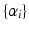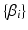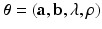The observations $\mathbf {y}$ include biomarker measurements $\{\mathbf {y}_{ij}\}$ at each visit. The hidden variables $\mathbf {u}$ are the subject-specific parameters $\{\alpha _i\}$ and $\{\beta _i\}$ . The unknown parameters are $\varvec{\theta }= (\mathbf {a}, \mathbf {b}, \lambda , \rho )$ .

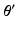E-Step: Let $\varvec{\theta }'$ be the previous estimate of the parameters. The expectation step involves evaluating an expression for

$\begin{aligned} E \left[ \ell \left( \mathbf {y}, \mathbf {u} \mid \varvec{\theta } \right) \mid \mathbf {y}, \varvec{\theta }' \right]= & {} \sum _i \int f(\tilde{\mathbf {u}}_i \mid \mathbf {y}_i, \varvec{\theta }') \ell \left( \mathbf {y}_i, \tilde{\mathbf {u}}_i \mid \varvec{\theta }\right) d\tilde{\mathbf {u}}_i. \end{aligned}$

(4)

Note that

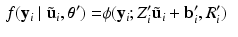
$\begin{aligned} f(\mathbf {y}_i \mid \tilde{\mathbf {u}}_i, \varvec{\theta }')= & {} \phi (\mathbf {y}_i; Z_i' \tilde{\mathbf {u}}_i + \mathbf {b}'_i, R'_i) \end{aligned}$

(5)

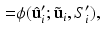
$\begin{aligned}= & {} \phi (\hat{\mathbf {u}}'_i; \tilde{\mathbf {u}}_i, S'_i), \end{aligned}$

(6)

where

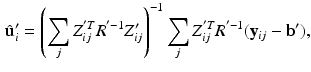
$\begin{aligned} \hat{\mathbf {u}}'_i = \left( \sum _{j} {Z^{'T}_{ij}} R^{'-1}Z'_{ij} \right) ^{-1} \sum _{j} {Z^{'T}_{ij}} R^{'-1}(\mathbf {y}_{ij} - \mathbf {b}'), \end{aligned}$

(7)

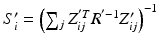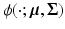$S'_i = \left( \sum _j {Z^{'T}_{ij}} R^{'-1} Z'_{ij} \right) ^{-1}$ , and $\phi (\cdot ; \varvec{\mu }, \varvec{\Sigma })$ is a multivariate Gaussian density with mean 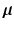$\varvec{\mu }$ and covariance 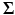$\varvec{\Sigma }$ . For ease of notation, we have used 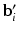$\mathbf {b}'_i$ to denote 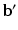$\mathbf {b}'$ stacked across the visits of subject i and $$R'_i$$

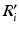to denote diagonally stacked $$R'$$

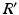matrices across the visits of subject i. $$Z'_i$$

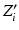is obtained by diagonally stacking 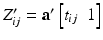$Z'_{ij}= \mathbf {a}' \begin{bmatrix} t_{ij}&1 \end{bmatrix}$ across the visits of subject i.

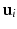The uniform prior assumption on $\mathbf {u}_i$ allows us to write 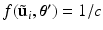$f(\tilde{\mathbf {u}}_i, \varvec{\theta }') = 1/c$ , where c is a constant. Rewriting the expectation using Bayes’ rule and plugging in the result from (6) yields

$\begin{aligned} E \left[ \ell \left( \mathbf {y}, \mathbf {u} \mid \varvec{\theta }\right) \mid \mathbf {y}, \varvec{\theta }' \right]\propto & {} \sum _i \int _\Omega \frac{\phi (\hat{\mathbf {u}}'_i; \tilde{\mathbf {u}}_i, S'_i)}{f(\mathbf {y}_i,\varvec{\theta }')} \ell \left( \mathbf {y}_i, \tilde{\mathbf {u}}_i \mid \varvec{\theta }\right) d\tilde{\mathbf {u}}_i. \end{aligned}$

(8)

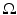If $\Omega$ is large enough, we can approximate the expectation as an infinite domain integration over 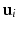$\mathbf {u}_i$ to obtain

$\begin{aligned} E \left[ \ell \left( \mathbf {y}, \mathbf {u} \mid \varvec{\theta }\right) \mid \mathbf {y}, \varvec{\theta }' \right]\propto & {} \sum _i \int \phi (\hat{\mathbf {u}}'_i; \tilde{\mathbf {u}}_i, S'_i) \ell \left( \mathbf {y}_i, \tilde{\mathbf {u}}_i \mid \varvec{\theta }\right) d\tilde{\mathbf {u}}_i \\\propto & {} -\sum _{i,j} \log [\det R] -\sum _{i,j} (\mathbf {y}_{ij} - \mathbf {b})^T R^{-1} (\mathbf {y}_{ij} - \mathbf {b}) \nonumber \\&+ 2 \left( \sum _{i,j} s'_{ij} \mathbf {y}_{ij} - \mathbf {b} \sum _{i,j} s'_{ij} \right) ^T R^{-1} \mathbf {a} \nonumber \end{aligned}$

(9)

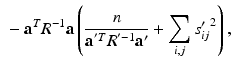
$\begin{aligned}&- \mathbf {a}^T R^{-1} \mathbf {a} \left( \frac{n}{\mathbf {a}^{'T} R^{'-1} \mathbf {a}'} + \sum _{i,j} {{s'_{ij}}^2} \right) , \end{aligned}$

(10)

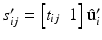where $s'_{ij} = \begin{bmatrix} t_{ij}&1 \end{bmatrix} \hat{\mathbf {u}}'_i$ .

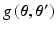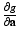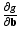M-Step: Let $g \left( \varvec{\theta }, \varvec{\theta }' \right)$ be the function obtained at the end of the E-step. We set the derivatives $\frac{\partial g}{\partial \mathbf {a}}$ and $\frac{\partial g}{\partial \mathbf {b}}$ equal to 0 and solve for the parameters to obtain

$\begin{aligned} \mathbf {a}= & {} \frac{\sum _{i,j} s'_{ij} (\mathbf {y}_{ij} - \bar{\mathbf {y}}) }{ \frac{2n}{\mathbf {a}^{'T} R^{'-1} \mathbf {a}'} + \sum _{i,j} {s'_{ij}}^2 - \frac{1}{\sum _i v_i} {\left( \sum _{i,j} s'_{ij} \right) }^2}, \end{aligned}$

(11)

$\begin{aligned} \mathbf {b}= & {} \frac{ \left( \frac{2n}{{\mathbf {a}'}^T R^{'-1} \mathbf {a}'} + \sum _{i,j} {s'_{ij}}^2 \right) \left( \sum _{i,j}\mathbf {y}_{ij} \right) - \left( \sum _{i,j} s'_{ij} \right) \left( \sum _{i,j} s'_{ij} \mathbf {y}_{ij} \right) }{ \left( \sum _i v_i \right) \left( \frac{2n}{\mathbf {a}^{'T} R^{'-1} \mathbf {a}'} + \sum _{i,j} {s'_{ij}}^2 \right) - \left( \sum _{i,j} s'_{ij} \right) ^2 }, \end{aligned}$