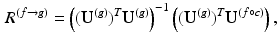Fig. 1.
Spectral Decomposition on Shapes – Any function f(x) on surface 1 (top row), or g(x) on surface 2 (bottom row) can be written as a sum of weighted harmonics (coloring is harmonic amplitude). Spectral weights, 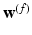 and
and 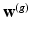 , are not directly transferable between surfaces since harmonics may change sign (bases 8), and not correspond (differences in black isolines, incompatible bases 80) (Color figure online).
, are not directly transferable between surfaces since harmonics may change sign (bases 8), and not correspond (differences in black isolines, incompatible bases 80) (Color figure online).
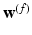 and
and 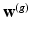 , are not directly transferable between surfaces since harmonics may change sign (bases 8), and not correspond (differences in black isolines, incompatible bases 80) (Color figure online).
, are not directly transferable between surfaces since harmonics may change sign (bases 8), and not correspond (differences in black isolines, incompatible bases 80) (Color figure online).Spectral graph theory [13] recently offers a fast alternative for matching high-resolution cortical surfaces within minutes on a conventional laptop computer [14, 15]. Spectral methods facilitate the correspondence problem by matching shapes in a spectral domain, rather than in the Euclidean space. Complex geometries, such as cortical surfaces, become reduced embeddings that are isometry-invariant, i.e., two shapes having the same intrinsic geometry, with identical geodesic distances between points, yield identical spectral embeddings, even if they have different extrinsic geometries. This is equivalent to comparing intrinsic vibration properties of shapes rather than their external configurations. However, a perturbation in shape isometry, such as expansion and compression of surfaces, changes the Laplacian eigenvectors in the spectral embeddings. This limited the use of spectral methods to coarse alignment [16] or global analysis [17, 18]. Attempts were made to correct the perturbed embeddings with rigid [19] and nonrigid transformations [14, 20], but all assume that Laplacian eigenvectors are compatible between shapes. These methods are in fact inherently flawed by the instability of the eigendecomposition. Eigenvectors can indeed change sign, orientation and shape, due to possible multiplicities of eigenvalues, to ambiguities in shape symmetry, and to numerical instabilities. For instance, the Laplacian eigenvectors of a sphere have ambiguous orientations. This makes spectral embeddings hardly comparable for near spherical shapes. The underlying graph metric may also be adapted by an expensive conformal metric correction [21]. Laplacian eigenvectors provide nonetheless a set of basis functions on complex geometries [22–24], and enable, therefore, any surface function to be represented as a linear combination of harmonics. This is for instance exploited in Laplacian smoothing [25, 26], where meshes are reconstructed with the coarser harmonics. The weights associated with each harmonic, capture intrinsic geometrical properties of the represented shape or function. These weights remain, however, incompatible between surfaces.


Fig. 2.
Spectral Transfer between Shapes – (a) Reconstruction of a function (here the point coordinates of mesh 1, 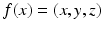 ), is correct when using the right eigenbasis of mesh 1. (b) Direct transfer of spectral weights,
), is correct when using the right eigenbasis of mesh 1. (b) Direct transfer of spectral weights, 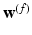 , onto mesh 2 yields a wrong reconstruction. (c) Transfer must account for an optimal spectral transformation R. Color represents sulcal depth on respective meshes. Transfer of
, onto mesh 2 yields a wrong reconstruction. (c) Transfer must account for an optimal spectral transformation R. Color represents sulcal depth on respective meshes. Transfer of 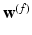 onto mesh 2 enables a direct comparison between depth maps (a,c) (Color figure online).
onto mesh 2 enables a direct comparison between depth maps (a,c) (Color figure online).
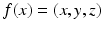 ), is correct when using the right eigenbasis of mesh 1. (b) Direct transfer of spectral weights,
), is correct when using the right eigenbasis of mesh 1. (b) Direct transfer of spectral weights, 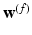 , onto mesh 2 yields a wrong reconstruction. (c) Transfer must account for an optimal spectral transformation R. Color represents sulcal depth on respective meshes. Transfer of
, onto mesh 2 yields a wrong reconstruction. (c) Transfer must account for an optimal spectral transformation R. Color represents sulcal depth on respective meshes. Transfer of 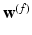 onto mesh 2 enables a direct comparison between depth maps (a,c) (Color figure online).
onto mesh 2 enables a direct comparison between depth maps (a,c) (Color figure online).This paper proposes to ameliorate spectral approaches by enabling a Spectral Transfer of such weights across interchangeable harmonic bases. Surface functions, such as point coordinates or activation maps, become transferable from one surface onto another via a spectral transformation of the harmonic weights. We indeed assume that if any function can be expressed using a surface basis, there exist a transformation allowing the harmonic weights on one surface to be transferred on another surface [23, 24]. In other words, a set of harmonic weights from one surface must be translated to the same language as on another surface. This requires the optimization of a spectral transformation matrix that combines both, a surface correspondence and a change of harmonic basis. Such spectral transfer provides a more robust formulation for spectral methods and handles naturally the sign changes as well as differences across Laplacian eigenvectors, including the mixing of eigenvectors in higher frequencies. In addition, this paper proposes Focused Harmonics in order to better capture geometrical properties within a region of interest. This is achieved by building a confidence map with a graph node weighting, which guides the spectral decomposition within regions of higher confidence. Localized functional maps, such as the visual area in the occipital lobe, can therefore be expressed with dedicated harmonics.
Our framework, Brain Transfer, enables the transfer of harmonic weights representing cortical shape and functional data across individuals. These harmonic weights capture intrinsic geometrical properties at multiscales, and can be linearly composed in order to reconstruct shapes and functions between subjects. We explore the parameter space of these harmonic weights via a principal component analysis over a dataset on retinotopy. Our results shows that our framework achieves similar accuracy in a fraction of the time as compared with conventional methods when matching cortical surfaces, and outperforms the state-of-the-art when matching functional data within the visual cortex.
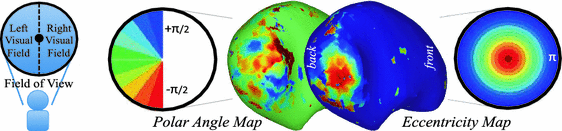

Fig. 3.
Retinotopy – fMRI activation maps of visual inputs over the visual field: (Left) Polar angle map, varying with ![$$[-\pi /2, +\pi /2]$$](/wp-content/uploads/2016/09/A339424_1_En_37_Chapter_IEq6.gif) (lower/upper field), (Right) Eccentricity map, varying with
(lower/upper field), (Right) Eccentricity map, varying with ![$$[0, \pi ]$$](/wp-content/uploads/2016/09/A339424_1_En_37_Chapter_IEq7.gif) (center/peripheral). Brain shows occipital lobe.
(center/peripheral). Brain shows occipital lobe.
![$$[-\pi /2, +\pi /2]$$](/wp-content/uploads/2016/09/A339424_1_En_37_Chapter_IEq6.gif) (lower/upper field), (Right) Eccentricity map, varying with
(lower/upper field), (Right) Eccentricity map, varying with ![$$[0, \pi ]$$](/wp-content/uploads/2016/09/A339424_1_En_37_Chapter_IEq7.gif) (center/peripheral). Brain shows occipital lobe.
(center/peripheral). Brain shows occipital lobe.2 Spectral Decomposition on Shapes
We begin by reviewing the fundamentals of spectral decomposition on shapes.
Surface Function Decomposition. Let us consider a compact manifold 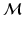 , and f(x) a smooth function on
, and f(x) a smooth function on 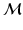 . The Laplace-Beltrami operator on f is defined as the divergence of the function gradient,
. The Laplace-Beltrami operator on f is defined as the divergence of the function gradient, 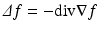 , and admits an eigendecomposition
, and admits an eigendecomposition 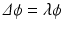 . This can be interpreted as finding the natural vibration amplitudes
. This can be interpreted as finding the natural vibration amplitudes 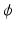 , at harmonic frequencies
, at harmonic frequencies 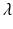 , of a membrane with shape
, of a membrane with shape  . Since
. Since 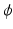 forms a basis on
forms a basis on 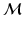 , any smooth function f can be represented as a linear combination
, any smooth function f can be represented as a linear combination 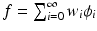 , where
, where 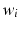 ’s are harmonic weights. On a discrete representation, e.g., a triangulated mesh of
’s are harmonic weights. On a discrete representation, e.g., a triangulated mesh of 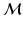 , the general Graph Laplacian is often used. Let us build the graph
, the general Graph Laplacian is often used. Let us build the graph 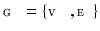 from the set of vertices, with positions
from the set of vertices, with positions 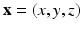 , and the set of edges. We define the
, and the set of edges. We define the 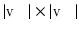 weighted adjacency matrix W in terms of node affinities, e.g.,
weighted adjacency matrix W in terms of node affinities, e.g., 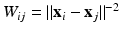 , and the diagonal degree matrix D as the sum
, and the diagonal degree matrix D as the sum 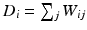 . The General Graph Laplacian is formulated as
. The General Graph Laplacian is formulated as 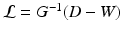 [27], where G is a general node weighting matrix, typically diagonal with
[27], where G is a general node weighting matrix, typically diagonal with 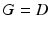 . The decomposition,
. The decomposition, 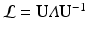 , provides the eigenvalues
, provides the eigenvalues 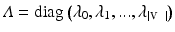 and its associated eigenfunctions
and its associated eigenfunctions 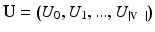 , that correspond respectively to the shape harmonic frequencies and bases on
, that correspond respectively to the shape harmonic frequencies and bases on 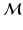 . Figure 1 shows how harmonics describe increasingly more complex geometrical properties as frequency augments. A surface function f is represented with:
. Figure 1 shows how harmonics describe increasingly more complex geometrical properties as frequency augments. A surface function f is represented with:
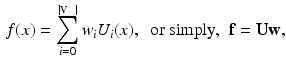
where 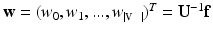 is a column vector of harmonic weights. When
is a column vector of harmonic weights. When 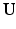 is truncated, we compute the first k coefficients with:
is truncated, we compute the first k coefficients with: 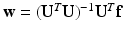 .
.
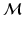 , and f(x) a smooth function on
, and f(x) a smooth function on 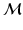 . The Laplace-Beltrami operator on f is defined as the divergence of the function gradient,
. The Laplace-Beltrami operator on f is defined as the divergence of the function gradient, 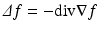 , and admits an eigendecomposition
, and admits an eigendecomposition 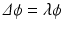 . This can be interpreted as finding the natural vibration amplitudes
. This can be interpreted as finding the natural vibration amplitudes 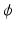 , at harmonic frequencies
, at harmonic frequencies 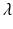 , of a membrane with shape
, of a membrane with shape 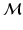 . Since
. Since 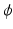 forms a basis on
forms a basis on 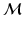 , any smooth function f can be represented as a linear combination
, any smooth function f can be represented as a linear combination 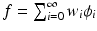 , where
, where 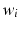 ’s are harmonic weights. On a discrete representation, e.g., a triangulated mesh of
’s are harmonic weights. On a discrete representation, e.g., a triangulated mesh of  , the general Graph Laplacian is often used. Let us build the graph
, the general Graph Laplacian is often used. Let us build the graph 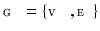 from the set of vertices, with positions
from the set of vertices, with positions 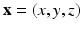 , and the set of edges. We define the
, and the set of edges. We define the 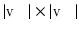 weighted adjacency matrix W in terms of node affinities, e.g.,
weighted adjacency matrix W in terms of node affinities, e.g., 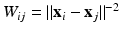 , and the diagonal degree matrix D as the sum
, and the diagonal degree matrix D as the sum 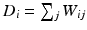 . The General Graph Laplacian is formulated as
. The General Graph Laplacian is formulated as 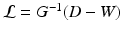 [27], where G is a general node weighting matrix, typically diagonal with
[27], where G is a general node weighting matrix, typically diagonal with 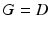 . The decomposition,
. The decomposition, 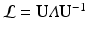 , provides the eigenvalues
, provides the eigenvalues 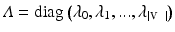 and its associated eigenfunctions
and its associated eigenfunctions 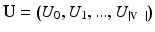 , that correspond respectively to the shape harmonic frequencies and bases on
, that correspond respectively to the shape harmonic frequencies and bases on 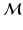 . Figure 1 shows how harmonics describe increasingly more complex geometrical properties as frequency augments. A surface function f is represented with:
. Figure 1 shows how harmonics describe increasingly more complex geometrical properties as frequency augments. A surface function f is represented with: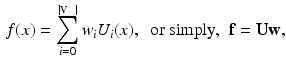
(1)
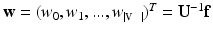 is a column vector of harmonic weights. When
is a column vector of harmonic weights. When  is truncated, we compute the first k coefficients with:
is truncated, we compute the first k coefficients with: 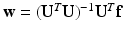 .
.Focused Decomposition. We propose a new focused spectral decomposition in a region of interest by exploiting a graph node weighting as a confidence map. This is of interest to fMRI, where signal is often localized in specific neural areas, such as in the visual cortex for retinotopy (Fig. 3). Node weighting is typically 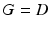 , which makes the Graph Laplacian a stochastic matrix. Each node has equal chances of occurring, i.e., row sum of
, which makes the Graph Laplacian a stochastic matrix. Each node has equal chances of occurring, i.e., row sum of 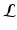 is 1. When a confidence map g(x) is used in place, the total node probability is changed with
is 1. When a confidence map g(x) is used in place, the total node probability is changed with 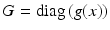 in
in 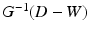 . Nodes are given importance with g(x), and stronger nodes become dominant in the Laplacian matrix. The spectral decomposition consequently becomes focused on these stronger graph nodes, yielding what we call Focused Harmonics (Fig. 4). In our experiment on functional data, the map is set as the signal difference in a common area between subjects, i.e., high signal difference between subjects indicates low confidence areas.
. Nodes are given importance with g(x), and stronger nodes become dominant in the Laplacian matrix. The spectral decomposition consequently becomes focused on these stronger graph nodes, yielding what we call Focused Harmonics (Fig. 4). In our experiment on functional data, the map is set as the signal difference in a common area between subjects, i.e., high signal difference between subjects indicates low confidence areas.

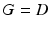 , which makes the Graph Laplacian a stochastic matrix. Each node has equal chances of occurring, i.e., row sum of
, which makes the Graph Laplacian a stochastic matrix. Each node has equal chances of occurring, i.e., row sum of 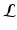 is 1. When a confidence map g(x) is used in place, the total node probability is changed with
is 1. When a confidence map g(x) is used in place, the total node probability is changed with 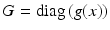 in
in 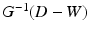 . Nodes are given importance with g(x), and stronger nodes become dominant in the Laplacian matrix. The spectral decomposition consequently becomes focused on these stronger graph nodes, yielding what we call Focused Harmonics (Fig. 4). In our experiment on functional data, the map is set as the signal difference in a common area between subjects, i.e., high signal difference between subjects indicates low confidence areas.
. Nodes are given importance with g(x), and stronger nodes become dominant in the Laplacian matrix. The spectral decomposition consequently becomes focused on these stronger graph nodes, yielding what we call Focused Harmonics (Fig. 4). In our experiment on functional data, the map is set as the signal difference in a common area between subjects, i.e., high signal difference between subjects indicates low confidence areas.
Fig. 4.
Focused Spectral Decomposition in Region of Interest – A confidence map indicates regions of confidence of a surface function. (Left) Higher confidence is given to the visual cortex, (Right) 1 to 10
to 10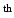 harmonics. Stronger graph node weights produce focused harmonics, with more description in ROI.
harmonics. Stronger graph node weights produce focused harmonics, with more description in ROI.
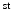 to 10
to 10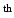 harmonics. Stronger graph node weights produce focused harmonics, with more description in ROI.
harmonics. Stronger graph node weights produce focused harmonics, with more description in ROI.Spectral Smoothing. Functions on surfaces can be represented with general, or focused harmonics, 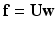 . One application is smoothing of meshes or surface functions. For instance, surface point coordinates
. One application is smoothing of meshes or surface functions. For instance, surface point coordinates 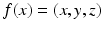 can be reconstructed using the first k low-frequency harmonics:
can be reconstructed using the first k low-frequency harmonics: 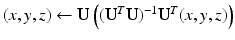 where the basis is truncated with
where the basis is truncated with 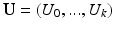 , and has size
, and has size 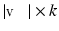 . Similarly, surface functions, such as retinotopy, can be smoothed on the surface by reconstructing the original maps with k harmonics. Figure 5 shows such reconstructions and illustrates how geometrical details appear with more harmonics.
. Similarly, surface functions, such as retinotopy, can be smoothed on the surface by reconstructing the original maps with k harmonics. Figure 5 shows such reconstructions and illustrates how geometrical details appear with more harmonics.
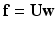 . One application is smoothing of meshes or surface functions. For instance, surface point coordinates
. One application is smoothing of meshes or surface functions. For instance, surface point coordinates 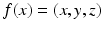 can be reconstructed using the first k low-frequency harmonics:
can be reconstructed using the first k low-frequency harmonics: 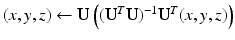 where the basis is truncated with
where the basis is truncated with 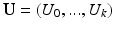 , and has size
, and has size 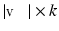 . Similarly, surface functions, such as retinotopy, can be smoothed on the surface by reconstructing the original maps with k harmonics. Figure 5 shows such reconstructions and illustrates how geometrical details appear with more harmonics.
. Similarly, surface functions, such as retinotopy, can be smoothed on the surface by reconstructing the original maps with k harmonics. Figure 5 shows such reconstructions and illustrates how geometrical details appear with more harmonics.3 Spectral Transfer
Let us now consider the functions 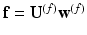 on a mesh
on a mesh 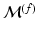 , and
, and 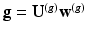 on a mesh
on a mesh 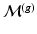 , and see how their intrinsic geometrical properties are transferred across meshes.
, and see how their intrinsic geometrical properties are transferred across meshes.
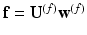 on a mesh
on a mesh 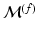 , and
, and 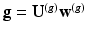 on a mesh
on a mesh 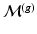 , and see how their intrinsic geometrical properties are transferred across meshes.
, and see how their intrinsic geometrical properties are transferred across meshes.Brain Matching. Conventional spectral matching methods rely on the principle that harmonic bases are compatible between meshes. A dense point matching is established via fast nearest-neighbor searches between spectral representations, typically 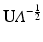 . However, this approach inherently suffers from the instability of eigenvectors, due to a sign or multiplicity ambiguity in a spectral decomposition. Eigenvectors may even be mixed in higher frequencies, which yield incompatible bases between meshes. Spectral methods typically compensate for these issues with a rigid or non-rigid transformation of spectral representations, but fail in addressing the fundamental incompatibility of harmonics between meshes. Recently, a double-layered spectral graph decomposition was proposed in [15], where the graph Laplacian is augmented by incorporating in the same Laplacian matrix, the two original meshes with a correspondence map between them. The decomposition of such joint graph Laplacian produces one unique set of harmonics, common to both surfaces. Correspondence links between such joint Harmonics may be interpreted as shortest random-walk distances between surfaces [15].
. However, this approach inherently suffers from the instability of eigenvectors, due to a sign or multiplicity ambiguity in a spectral decomposition. Eigenvectors may even be mixed in higher frequencies, which yield incompatible bases between meshes. Spectral methods typically compensate for these issues with a rigid or non-rigid transformation of spectral representations, but fail in addressing the fundamental incompatibility of harmonics between meshes. Recently, a double-layered spectral graph decomposition was proposed in [15], where the graph Laplacian is augmented by incorporating in the same Laplacian matrix, the two original meshes with a correspondence map between them. The decomposition of such joint graph Laplacian produces one unique set of harmonics, common to both surfaces. Correspondence links between such joint Harmonics may be interpreted as shortest random-walk distances between surfaces [15].
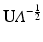 . However, this approach inherently suffers from the instability of eigenvectors, due to a sign or multiplicity ambiguity in a spectral decomposition. Eigenvectors may even be mixed in higher frequencies, which yield incompatible bases between meshes. Spectral methods typically compensate for these issues with a rigid or non-rigid transformation of spectral representations, but fail in addressing the fundamental incompatibility of harmonics between meshes. Recently, a double-layered spectral graph decomposition was proposed in [15], where the graph Laplacian is augmented by incorporating in the same Laplacian matrix, the two original meshes with a correspondence map between them. The decomposition of such joint graph Laplacian produces one unique set of harmonics, common to both surfaces. Correspondence links between such joint Harmonics may be interpreted as shortest random-walk distances between surfaces [15].
. However, this approach inherently suffers from the instability of eigenvectors, due to a sign or multiplicity ambiguity in a spectral decomposition. Eigenvectors may even be mixed in higher frequencies, which yield incompatible bases between meshes. Spectral methods typically compensate for these issues with a rigid or non-rigid transformation of spectral representations, but fail in addressing the fundamental incompatibility of harmonics between meshes. Recently, a double-layered spectral graph decomposition was proposed in [15], where the graph Laplacian is augmented by incorporating in the same Laplacian matrix, the two original meshes with a correspondence map between them. The decomposition of such joint graph Laplacian produces one unique set of harmonics, common to both surfaces. Correspondence links between such joint Harmonics may be interpreted as shortest random-walk distances between surfaces [15].
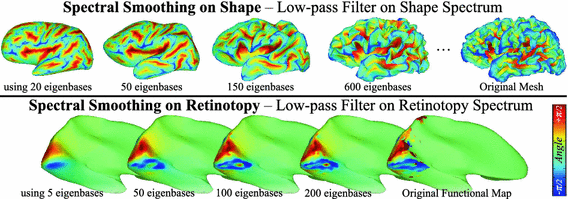
Fig. 5.
Spectral Smoothing – (Top) Reconstruction of a surface using 20 to 600 eigenbases. Note how the brain convolves with more eigenbases. (Bottom) Reconstruction of retinotopy (polar angle map) using 5 to 200 eigenbases. Few focused harmonics are sufficient to reconstruct the polar map.
Brain Transfer. We propose a new approach for brain matching, where intrinsic geometrical properties are transferred across brains instead of being matched. This transfer addresses the inherent issues on eigenvector incompatibility in spectral methods. It was shown earlier that intrinsic geometrical properties of shapes or functions are captured in harmonic weights, and that shapes and functions can be reconstructed using such weights. However, harmonic weights are not directly interchangeable between meshes. Figure 2-b shows an invalid direct transfer with 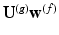 , which does not produce the excepted shape of
, which does not produce the excepted shape of 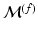 . Central to our method is the ability to transfer intrinsic geometrical information between brains, via an optimal spectral transformation of harmonic weights. We assume there exists a spectral transformation
. Central to our method is the ability to transfer intrinsic geometrical information between brains, via an optimal spectral transformation of harmonic weights. We assume there exists a spectral transformation 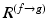 between
between 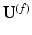 and
and 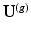 [22–24]. This corresponds to a change of basis
[22–24]. This corresponds to a change of basis 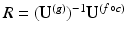 , where c is an unknown correspondence map that matches rows of
, where c is an unknown correspondence map that matches rows of 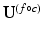 with equivalent rows of
with equivalent rows of 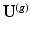 . Such transformation permits the spectral transfer of
. Such transformation permits the spectral transfer of 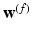 between meshes, such that
between meshes, such that 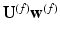 becomes equivalent to
becomes equivalent to 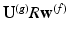 , which uses a different basis. In practice, only
, which uses a different basis. In practice, only 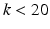 coefficients
coefficients 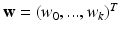 are required in brain matching. The
are required in brain matching. The 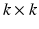 spectral transformation matrix from
spectral transformation matrix from 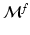 to
to 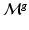 is computed with the truncated basis
is computed with the truncated basis 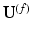 and
and 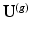 :
:
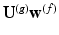 , which does not produce the excepted shape of
, which does not produce the excepted shape of 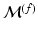 . Central to our method is the ability to transfer intrinsic geometrical information between brains, via an optimal spectral transformation of harmonic weights. We assume there exists a spectral transformation
. Central to our method is the ability to transfer intrinsic geometrical information between brains, via an optimal spectral transformation of harmonic weights. We assume there exists a spectral transformation 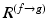 between
between 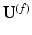 and
and 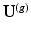 [22–24]. This corresponds to a change of basis
[22–24]. This corresponds to a change of basis 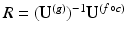 , where c is an unknown correspondence map that matches rows of
, where c is an unknown correspondence map that matches rows of 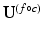 with equivalent rows of
with equivalent rows of 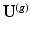 . Such transformation permits the spectral transfer of
. Such transformation permits the spectral transfer of 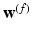 between meshes, such that
between meshes, such that 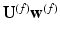 becomes equivalent to
becomes equivalent to 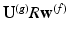 , which uses a different basis. In practice, only
, which uses a different basis. In practice, only 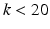 coefficients
coefficients 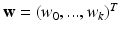 are required in brain matching. The
are required in brain matching. The 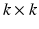 spectral transformation matrix from
spectral transformation matrix from 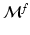 to
to 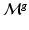 is computed with the truncated basis
is computed with the truncated basis 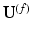 and
and 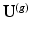 :
: