and diffusion coefficient 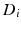 , and a hindered extracellular compartment with volume fraction
, and a hindered extracellular compartment with volume fraction 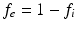 and diffusion coefficient
and diffusion coefficient 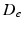 . The DW-MRI signal, S, is given by
. The DW-MRI signal, S, is given by
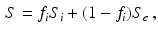
(1)
![$$\begin{aligned} \begin{aligned} S_i&= \text {exp}\left( -2\gamma ^2G^2\sum _{m=1}^\infty \frac{1}{\alpha _m^2(\alpha _m^2R^2 - 2)}\left[ \frac{2\delta }{\alpha _m^2D_i} \right. \right. \\&\quad \quad \left. \left. + \frac{2e^{-\alpha _m^2D_i\delta } + 2e^{-\alpha _m^2D_i\varDelta } - e^{-\alpha _m^2D_i(\varDelta -\delta )} - e^{-\alpha _m^2D_i(\varDelta +\delta )} -2}{\alpha _m^4D_i^2}\right] \right) , \end{aligned} \end{aligned}$$](/wp-content/uploads/2016/09/A339424_1_En_14_Chapter_Equ2.gif)
(2)
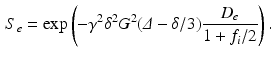
(3)
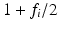 [20]. The
[20]. The 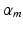 in (2) is obtained from the mth root of
in (2) is obtained from the mth root of 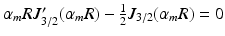 , where
, where 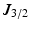 is the Bessel function of the first kind, order 3 / 2 [18, 19]. The signals calculated analytically from (1)–(3) were compared with synthetic signals generated from Monte Carlo diffusion simulations. The Camino toolkit [8] was used to perform random walk simulations in a 3D geometry of monodisperse, packed impermeable spheres. All simulations had spatial and temporal resolutions of 0.655
is the Bessel function of the first kind, order 3 / 2 [18, 19]. The signals calculated analytically from (1)–(3) were compared with synthetic signals generated from Monte Carlo diffusion simulations. The Camino toolkit [8] was used to perform random walk simulations in a 3D geometry of monodisperse, packed impermeable spheres. All simulations had spatial and temporal resolutions of 0.655 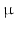 m and 0.0357 ms, respectively, used 195000 walkers and had intra- and extra-cellular diffusion coefficients set to
m and 0.0357 ms, respectively, used 195000 walkers and had intra- and extra-cellular diffusion coefficients set to 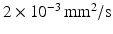 . Models with different cell sizes (
. Models with different cell sizes (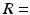 7–30
7–30 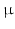 m) and intracellular volume fractions (
m) and intracellular volume fractions (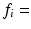 0.16–0.71) were used in separate simulations. For each combination of R and
0.16–0.71) were used in separate simulations. For each combination of R and 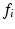 , synthetic signals were generated for PGSE sequences with a range of gradient strengths,
, synthetic signals were generated for PGSE sequences with a range of gradient strengths, 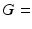 0–263 mT/m, and separations,
0–263 mT/m, and separations, 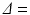 12–45 ms, with the gradient duration
12–45 ms, with the gradient duration 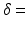 4 ms. These sequence parameters can be obtained on preclinical scanners, and match the range used in the phantom MR experiments (see below). Figure 1 shows an example of the geometry used in these simulations, and plots synthetic (circles) and analytic (dashed lines) signals as a function of G and
4 ms. These sequence parameters can be obtained on preclinical scanners, and match the range used in the phantom MR experiments (see below). Figure 1 shows an example of the geometry used in these simulations, and plots synthetic (circles) and analytic (dashed lines) signals as a function of G and 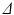 for different combinations of R and
for different combinations of R and 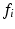 . In general, good agreement was found between the synthetic and analytic signals over a range of tissue properties and sequence parameters, with a maximum difference between simulated and analytic signals of 0.02. This suggests that (1)–(3) provide an accurate description of this simple tissue model.
. In general, good agreement was found between the synthetic and analytic signals over a range of tissue properties and sequence parameters, with a maximum difference between simulated and analytic signals of 0.02. This suggests that (1)–(3) provide an accurate description of this simple tissue model.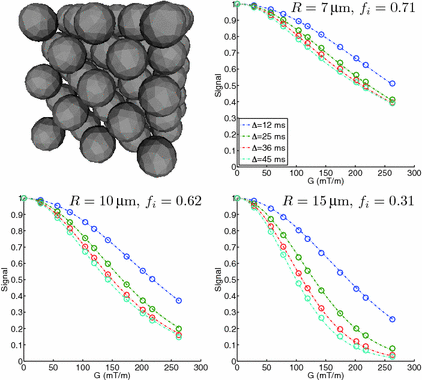
Fig. 1.
Spherical cell geometry used in the simulations, along with synthetic (circles) and analytic (dashed lines) signals plotted as a function of G and 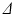 for different combinations of R and
for different combinations of R and 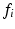 .
.
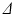 for different combinations of R and
for different combinations of R and 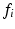 .
.3 Phantom Construction and Characterisation
Coaxial electrospraying was performed using polyethylene glycol (PEG) dissolved in chloroform for the core, and polycaprolactone (PCL) dissolved in chloroform for the shell. The PEG solution was injected into the inner needle of a coaxial spinneret at a flow rate of 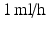 , while the PCL solution was injected into the outer needle at
, while the PCL solution was injected into the outer needle at 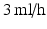 . A voltage of
. A voltage of 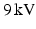 was applied between the spinneret and a ground electrode (a thin aluminium plate) placed
was applied between the spinneret and a ground electrode (a thin aluminium plate) placed 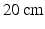 below. The core–shell spheres, which form as the liquid jet emerging from the spinneret breaks up, were collected on a copper wire placed on the ground electrode, forming a bulk sample over a period of
below. The core–shell spheres, which form as the liquid jet emerging from the spinneret breaks up, were collected on a copper wire placed on the ground electrode, forming a bulk sample over a period of 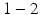 h. The wire was then removed, leaving a bulk sample structured as a hollow cylinder. Two parts of the bulk phantom were used for SEM and MR characterisation, respectively. For the MR experiments the phantom was placed in an NMR tube (
h. The wire was then removed, leaving a bulk sample structured as a hollow cylinder. Two parts of the bulk phantom were used for SEM and MR characterisation, respectively. For the MR experiments the phantom was placed in an NMR tube (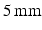 outer diameter), which was filled with cyclohexane approximately one week before scanning. Cyclohexane provides the MR signal in these experiments and was chosen instead of water as PCL is hydrophobic and therefore prevents water molecules reaching the intracellular space. The potential for using other polymers is currently being investigated, which may allow water to be used instead of cyclohexane.
outer diameter), which was filled with cyclohexane approximately one week before scanning. Cyclohexane provides the MR signal in these experiments and was chosen instead of water as PCL is hydrophobic and therefore prevents water molecules reaching the intracellular space. The potential for using other polymers is currently being investigated, which may allow water to be used instead of cyclohexane.
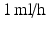 , while the PCL solution was injected into the outer needle at
, while the PCL solution was injected into the outer needle at 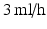 . A voltage of
. A voltage of 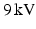 was applied between the spinneret and a ground electrode (a thin aluminium plate) placed
was applied between the spinneret and a ground electrode (a thin aluminium plate) placed 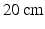 below. The core–shell spheres, which form as the liquid jet emerging from the spinneret breaks up, were collected on a copper wire placed on the ground electrode, forming a bulk sample over a period of
below. The core–shell spheres, which form as the liquid jet emerging from the spinneret breaks up, were collected on a copper wire placed on the ground electrode, forming a bulk sample over a period of 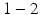 h. The wire was then removed, leaving a bulk sample structured as a hollow cylinder. Two parts of the bulk phantom were used for SEM and MR characterisation, respectively. For the MR experiments the phantom was placed in an NMR tube (
h. The wire was then removed, leaving a bulk sample structured as a hollow cylinder. Two parts of the bulk phantom were used for SEM and MR characterisation, respectively. For the MR experiments the phantom was placed in an NMR tube (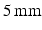 outer diameter), which was filled with cyclohexane approximately one week before scanning. Cyclohexane provides the MR signal in these experiments and was chosen instead of water as PCL is hydrophobic and therefore prevents water molecules reaching the intracellular space. The potential for using other polymers is currently being investigated, which may allow water to be used instead of cyclohexane.
outer diameter), which was filled with cyclohexane approximately one week before scanning. Cyclohexane provides the MR signal in these experiments and was chosen instead of water as PCL is hydrophobic and therefore prevents water molecules reaching the intracellular space. The potential for using other polymers is currently being investigated, which may allow water to be used instead of cyclohexane.From the part of the bulk sample set aside for SEM analysis, ten subsamples were taken and imaged with a Phenom G2 Pro desktop SEM. These ten SEM images were then used to estimate the size of the spheres. Analysis was carried out using ImageJ (National Institutes of Health, Bethesda, Maryland, USA, http://imagej.nih.gov/ij/), and began by selecting which spheres in each image would be measured. In order to avoid potential bias in choosing spheres manually, a grid was placed on each SEM image, and spheres which contained a grid intersection were chosen as potential candidates for measurement. Not all of these spheres could be measured, however, as spheres in the foreground could obstruct those behind. As such, candidate spheres were selected for measurement if two perpendicular lines could be drawn from one edge to another, approximately through the sphere centre, without other spheres occluding the edges. In some cases the edges merged with another sphere, making the boundary less well defined. In this way, two diameter measurements were made for each chosen sphere, with the final estimate taken as the mean of these two lengths. At least ten spheres per image were chosen for measurement, and the process was performed independently by two observers after deciding which spheres were to be analysed. The mean difference and limits of agreement were calculated to compare the two observers’ measurements [21]. For consistency with the MR analysis, the measurements are reported as sphere radii, as opposed to diameters. It should be noted that these measurements provide an estimate of the outer radius of the spheres, which is larger than the internal radius due to the non-zero thickness of the sphere walls.
4 MR Methods
4.1 MR Acquisition
MR experiments were carried out on a 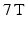 Bruker system (Bruker BioSpin, Ettlingen, Germany), using a transmit/receive volume coil. Data were acquired using four separate PGSE sequences, each with a different gradient separation:
Bruker system (Bruker BioSpin, Ettlingen, Germany), using a transmit/receive volume coil. Data were acquired using four separate PGSE sequences, each with a different gradient separation: 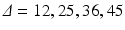 ms. For each
ms. For each 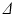 scan, images were acquired at seven gradient strengths: G = 0, 28.5, 78.1, 119, 147, 202, 263 mT/m;
scan, images were acquired at seven gradient strengths: G = 0, 28.5, 78.1, 119, 147, 202, 263 mT/m; 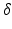 was fixed at 4 ms for each scan. In order to maximise signal to noise ratio (SNR), the lowest possible echo time (TE) was chosen for each
was fixed at 4 ms for each scan. In order to maximise signal to noise ratio (SNR), the lowest possible echo time (TE) was chosen for each 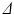 , giving TE = 21.2, 34.2, 45.2, 54.2 ms for
, giving TE = 21.2, 34.2, 45.2, 54.2 ms for 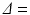 12, 25, 36, 45 ms, respectively. Each scan acquired images with three diffusion gradient directions, using a spin-echo readout with a
12, 25, 36, 45 ms, respectively. Each scan acquired images with three diffusion gradient directions, using a spin-echo readout with a 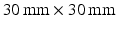 field of view,
field of view, 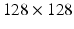 matrix,
matrix, 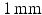 slice thickness and a
slice thickness and a 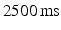 repetition time.
repetition time.
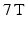 Bruker system (Bruker BioSpin, Ettlingen, Germany), using a transmit/receive volume coil. Data were acquired using four separate PGSE sequences, each with a different gradient separation:
Bruker system (Bruker BioSpin, Ettlingen, Germany), using a transmit/receive volume coil. Data were acquired using four separate PGSE sequences, each with a different gradient separation: 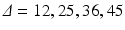 ms. For each
ms. For each 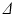 scan, images were acquired at seven gradient strengths: G = 0, 28.5, 78.1, 119, 147, 202, 263 mT/m;
scan, images were acquired at seven gradient strengths: G = 0, 28.5, 78.1, 119, 147, 202, 263 mT/m; 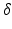 was fixed at 4 ms for each scan. In order to maximise signal to noise ratio (SNR), the lowest possible echo time (TE) was chosen for each
was fixed at 4 ms for each scan. In order to maximise signal to noise ratio (SNR), the lowest possible echo time (TE) was chosen for each 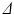 , giving TE = 21.2, 34.2, 45.2, 54.2 ms for
, giving TE = 21.2, 34.2, 45.2, 54.2 ms for 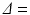 12, 25, 36, 45 ms, respectively. Each scan acquired images with three diffusion gradient directions, using a spin-echo readout with a
12, 25, 36, 45 ms, respectively. Each scan acquired images with three diffusion gradient directions, using a spin-echo readout with a 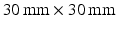 field of view,
field of view, 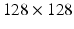 matrix,
matrix, 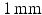 slice thickness and a
slice thickness and a 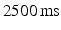 repetition time.
repetition time.4.2 MR Analysis
The phantom ROI was defined by thresholding the 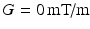 images to leave only the voxels within the phantom, excluding those containing the free cyclohexane. The equivalent voxels in each diffusion-weighted image were found, and the mean signal intensity taken for each G value to boost SNR. Repeating this for each
images to leave only the voxels within the phantom, excluding those containing the free cyclohexane. The equivalent voxels in each diffusion-weighted image were found, and the mean signal intensity taken for each G value to boost SNR. Repeating this for each 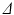 scan therefore gave ROI-averaged signal intensities as a function of G and
scan therefore gave ROI-averaged signal intensities as a function of G and 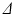 , which were then normalised to the unweighted signal for their respective
, which were then normalised to the unweighted signal for their respective 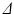 scans. The two-compartment analytic expression given by (1)–(3) was then fitted to these normalised signals. The free diffusivities in the intra- and extra-cellular spaces were assumed to be equal,
scans. The two-compartment analytic expression given by (1)–(3) was then fitted to these normalised signals. The free diffusivities in the intra- and extra-cellular spaces were assumed to be equal, 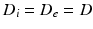 . Two methods of performing the fitting were investigated. First, the full four-parameter fit was carried out, yielding estimates of each model parameter (cell radius, R, intracellular volume fraction,
. Two methods of performing the fitting were investigated. First, the full four-parameter fit was carried out, yielding estimates of each model parameter (cell radius, R, intracellular volume fraction, 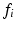 , free diffusivity, D, and unweighted signal,
, free diffusivity, D, and unweighted signal, 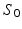 ) directly from the ROI-averaged phantom signals. Second, D was fixed during the optimisation, with the fit returning estimates of R,
) directly from the ROI-averaged phantom signals. Second, D was fixed during the optimisation, with the fit returning estimates of R, 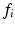 and
and 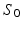 only. In this case, D was fixed at the value of the diffusion coefficient measured in the free cyclohexane, which serves as a ground truth measurement of the free diffusion coefficient. This value was obtained by averaging the median ADC values from a ROI in the free cyclohexane, over the different
only. In this case, D was fixed at the value of the diffusion coefficient measured in the free cyclohexane, which serves as a ground truth measurement of the free diffusion coefficient. This value was obtained by averaging the median ADC values from a ROI in the free cyclohexane, over the different 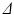 experiments and gradient directions. The ADC fits were performed on a voxel-wise basis using maximum likelihood (ML) fitting [22], with the full range of G for each
experiments and gradient directions. The ADC fits were performed on a voxel-wise basis using maximum likelihood (ML) fitting [22], with the full range of G for each 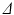 experiment. The ML method used a single Rician probability density function (PDF) in the objective function and was appropriate here as the signals used in the ADC fitting were not averaged [23].
experiment. The ML method used a single Rician probability density function (PDF) in the objective function and was appropriate here as the signals used in the ADC fitting were not averaged [23].
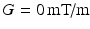 images to leave only the voxels within the phantom, excluding those containing the free cyclohexane. The equivalent voxels in each diffusion-weighted image were found, and the mean signal intensity taken for each G value to boost SNR. Repeating this for each
images to leave only the voxels within the phantom, excluding those containing the free cyclohexane. The equivalent voxels in each diffusion-weighted image were found, and the mean signal intensity taken for each G value to boost SNR. Repeating this for each 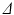 scan therefore gave ROI-averaged signal intensities as a function of G and
scan therefore gave ROI-averaged signal intensities as a function of G and 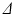 , which were then normalised to the unweighted signal for their respective
, which were then normalised to the unweighted signal for their respective 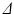 scans. The two-compartment analytic expression given by (1)–(3) was then fitted to these normalised signals. The free diffusivities in the intra- and extra-cellular spaces were assumed to be equal,
scans. The two-compartment analytic expression given by (1)–(3) was then fitted to these normalised signals. The free diffusivities in the intra- and extra-cellular spaces were assumed to be equal, 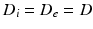 . Two methods of performing the fitting were investigated. First, the full four-parameter fit was carried out, yielding estimates of each model parameter (cell radius, R, intracellular volume fraction,
. Two methods of performing the fitting were investigated. First, the full four-parameter fit was carried out, yielding estimates of each model parameter (cell radius, R, intracellular volume fraction, 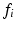 , free diffusivity, D, and unweighted signal,
, free diffusivity, D, and unweighted signal, 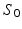 ) directly from the ROI-averaged phantom signals. Second, D was fixed during the optimisation, with the fit returning estimates of R,
) directly from the ROI-averaged phantom signals. Second, D was fixed during the optimisation, with the fit returning estimates of R, 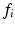 and
and 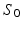 only. In this case, D was fixed at the value of the diffusion coefficient measured in the free cyclohexane, which serves as a ground truth measurement of the free diffusion coefficient. This value was obtained by averaging the median ADC values from a ROI in the free cyclohexane, over the different
only. In this case, D was fixed at the value of the diffusion coefficient measured in the free cyclohexane, which serves as a ground truth measurement of the free diffusion coefficient. This value was obtained by averaging the median ADC values from a ROI in the free cyclohexane, over the different 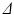 experiments and gradient directions. The ADC fits were performed on a voxel-wise basis using maximum likelihood (ML) fitting [22], with the full range of G for each
experiments and gradient directions. The ADC fits were performed on a voxel-wise basis using maximum likelihood (ML) fitting [22], with the full range of G for each 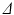 experiment. The ML method used a single Rician probability density function (PDF) in the objective function and was appropriate here as the signals used in the ADC fitting were not averaged [23].
experiment. The ML method used a single Rician probability density function (PDF) in the objective function and was appropriate here as the signals used in the ADC fitting were not averaged [23].For the microstructural estimates, the fitting procedure was repeated for a range of starting values, and the final result taken as the fit which gave the lowest value of the objective function. Three starting values were picked at random for each parameter, within a wide range of possible values: 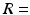 1–35
1–35 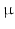 m,
m, 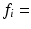 0–1,
0–1, 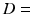 0.1–3.1
0.1–3.1 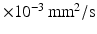 . The fitting was then repeated for each combination of these randomly chosen values, giving
. The fitting was then repeated for each combination of these randomly chosen values, giving 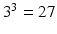 different fits; only one starting value was used for
different fits; only one starting value was used for 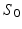 , which was 1. Picking 2, 3, 4, 5 or 6 starting values for each parameter (giving 8, 27, 64, 125 and 216 repeated fits, respectively) was observed to have negligible effect on the final results. Different random selections within the same range also had negligible effect on the results, suggesting that the values of the fitted parameters were not an artefact of the starting values. Apart from fixing D in the second fitting method, no constraints were applied to any of the fitted parameters. In contrast to the non-averaged signals used for the free cyclohexane ADC calculations, the fits to the two-compartment model used averaged signals, making the use of a single Rician PDF for ML fitting no longer appropriate [23]. As the PDF for averaged Rician-distributed signals has no closed-form expression, the ML method used above cannot be employed, and least squares (LS) fitting was used instead.
, which was 1. Picking 2, 3, 4, 5 or 6 starting values for each parameter (giving 8, 27, 64, 125 and 216 repeated fits, respectively) was observed to have negligible effect on the final results. Different random selections within the same range also had negligible effect on the results, suggesting that the values of the fitted parameters were not an artefact of the starting values. Apart from fixing D in the second fitting method, no constraints were applied to any of the fitted parameters. In contrast to the non-averaged signals used for the free cyclohexane ADC calculations, the fits to the two-compartment model used averaged signals, making the use of a single Rician PDF for ML fitting no longer appropriate [23]. As the PDF for averaged Rician-distributed signals has no closed-form expression, the ML method used above cannot be employed, and least squares (LS) fitting was used instead.
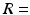 1–35
1–35 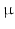 m,
m, 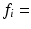 0–1,
0–1, 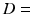 0.1–3.1
0.1–3.1 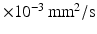 . The fitting was then repeated for each combination of these randomly chosen values, giving
. The fitting was then repeated for each combination of these randomly chosen values, giving 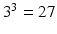 different fits; only one starting value was used for
different fits; only one starting value was used for 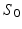 , which was 1. Picking 2, 3, 4, 5 or 6 starting values for each parameter (giving 8, 27, 64, 125 and 216 repeated fits, respectively) was observed to have negligible effect on the final results. Different random selections within the same range also had negligible effect on the results, suggesting that the values of the fitted parameters were not an artefact of the starting values. Apart from fixing D in the second fitting method, no constraints were applied to any of the fitted parameters. In contrast to the non-averaged signals used for the free cyclohexane ADC calculations, the fits to the two-compartment model used averaged signals, making the use of a single Rician PDF for ML fitting no longer appropriate [23]. As the PDF for averaged Rician-distributed signals has no closed-form expression, the ML method used above cannot be employed, and least squares (LS) fitting was used instead.
, which was 1. Picking 2, 3, 4, 5 or 6 starting values for each parameter (giving 8, 27, 64, 125 and 216 repeated fits, respectively) was observed to have negligible effect on the final results. Different random selections within the same range also had negligible effect on the results, suggesting that the values of the fitted parameters were not an artefact of the starting values. Apart from fixing D in the second fitting method, no constraints were applied to any of the fitted parameters. In contrast to the non-averaged signals used for the free cyclohexane ADC calculations, the fits to the two-compartment model used averaged signals, making the use of a single Rician PDF for ML fitting no longer appropriate [23]. As the PDF for averaged Rician-distributed signals has no closed-form expression, the ML method used above cannot be employed, and least squares (LS) fitting was used instead.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree




