3.5 %, 85.6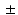 7.5 %, 87.4
7.5 %, 87.4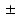 3.6 %, 9.7
3.6 %, 9.7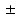 7.2 %, and 0.6
7.2 %, and 0.6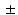 0.2 mm, respectively.
0.2 mm, respectively.
The rights of this work are transferred to the extent transferable according to title 17 U.S.C. 105.
1 Introduction
Pancreatic neuroendocrine tumors are abnormal growths of hormone-producing cells in the pancreas [4]. They are slow growing and usually not treated until reaching a certain size threshold. Similar to most tumors, pancreatic tumor growth is associated with cell invasion and mass effect [6]. In cell invasion, tumor cells migrate as a group and penetrate to the surrounding tissues. Mass effect is the result of expansive growth which increases the tumor volume, and the outward pushing may displace the tumor cells and surrounding tissues. Mass effect also contributes to and enhances cell invasion.
In image-based macroscopic tumor growth modeling, tumor cell invasion is mostly modeled through reaction-diffusion equations [3, 7, 9, 12, 18]. The differences among these models are usually the choices between isotropic and anisotropic diffusion, Gompertz and logistic cell proliferation, or with and without considering treatment effects. Because of the highly deformable nature of the pancreas, we concentrate on mass effect and tumor mechanical properties in this paper. Most works have modeled mass effect by explicitly enforcing tumor size change or by exerting tumor-density-induced forces to a mechanical model [3, 7, 13, 18]. In [3, 13], the mass effects of the brain glioma and its surrounding edema were modeled differently based on their physiological characteristics. In [3], the volume change of the bulk tumor core was modeled as an exponential function, and a penalty method was used to enforce the volume change via homogeneous pressure. For the edema, internal stresses proportional to the local tumor cell densities were introduced, thus the tumor and its surrounding structures are displaced by tumor-density-induced forces proportional to the negative gradients of the local tumor densities. In [13], the expansive force of the bulk tumor was approximated by constant outward pressure acting on the tumor boundary, and the growth of the edema was modeled as an isotropic expansive strain. In [7], using the edema model of [3], the tumor-density-induced forces were applied to the entire brain glioma. The forces were converted to velocities through a linear mechanical model, which were used in the advection term of a reaction-advection-diffusion equation to displace the tumor cell densities. In [18], the tumor-density-induced forces were adopted to model the mass effect of pancreatic tumor growth using finite element methods (FEM).
Despite the promising results, these models were mostly developed for brain tumors and may be inappropriate for pancreatic tumor growths. Different from the brain in the skull, the pancreas in the abdomen can be largely deformed by the body posture and its surrounding organs [5]. Therefore, the tumor shape difference observable from images is not only driven by the tumor growth, but also the motion of the pancreas. As images at different time points are used to infer the tumor growth properties during model personalization, the prediction accuracy may be reduced if such motion is not properly considered. For the approaches using tumor-density-induced forces [7, 18], the tumor volume change could not be explicitly modeled. These approaches, together with those converting the volume change into pressure [3, 13], modeled the tumor growth as stress-strain relation in continuum mechanics. First of all, this contradicts the nearly incompressible nature of most solid tumors, and thus the incompressibility of the mechanical model has to be compromised. Secondly, for the mechanical models with nonlinear constitutive laws, the tumor stiffness increases with its elastic volume change regardless of the underlying physiology, and this reduces the model accuracy.
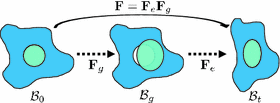
In view of these limitations, here we adopt the multiplicative growth decomposition for mass effect, which was initially introduced to study residual stresses in soft tissues [11, 15]. In this approach, the continuous deformation field of a body after growth can be decomposed into its growth and elastic parts (Fig. 1). The intermediate growth configuration can be stress-free but incompatible, which may have holes, overlaps, or other discontinuities. To maintain the continuity of the structure in reality, elastic deformation which generates residual stresses is applied to the growth deformation. With this decomposition, tumor growth can be modeled separately from the elastic part using explicit growth functions. This preserves the accuracy of the elastic response, and anisotropic mass effect can be easily incorporated. Moreover, with the relation between the growth and elastic parts, the deformation exerted by the surrounding structures on the tumor can be naturally included through displacement boundary conditions.
In this paper, the tumor growth model accounting for both cell invasion and mass effect is personalized using medical images. The tumor cell invasion is modeled as a reaction-diffusion equation. The mass effect is modeled through multiplicative growth decomposition [11], with the growth part modeled as orthotropic stretches with logistic functions, and the elastic part modeled using a hyperelastic constitutive law [8]. The tumor growth prediction is achieved through model parameter estimation using derivative-free optimization. Following [18], 2-[ F]-fluoro-2-deoxy-D-glucose positron emission tomographic (FDG-PET) images are used to compute the proliferation rates, and contrast-enhanced computed tomographic (CT) images are used to provide the local tumor cell densities. We also incorporate the displacements derived from post-contrast CT images to account for the pancreatic motion. Experiments were performed on synthetic and clinical data to compare the differences between using different models of mass effect and between with and without imaged-derived motion.
F]-fluoro-2-deoxy-D-glucose positron emission tomographic (FDG-PET) images are used to compute the proliferation rates, and contrast-enhanced computed tomographic (CT) images are used to provide the local tumor cell densities. We also incorporate the displacements derived from post-contrast CT images to account for the pancreatic motion. Experiments were performed on synthetic and clinical data to compare the differences between using different models of mass effect and between with and without imaged-derived motion.
 F]-fluoro-2-deoxy-D-glucose positron emission tomographic (FDG-PET) images are used to compute the proliferation rates, and contrast-enhanced computed tomographic (CT) images are used to provide the local tumor cell densities. We also incorporate the displacements derived from post-contrast CT images to account for the pancreatic motion. Experiments were performed on synthetic and clinical data to compare the differences between using different models of mass effect and between with and without imaged-derived motion.
F]-fluoro-2-deoxy-D-glucose positron emission tomographic (FDG-PET) images are used to compute the proliferation rates, and contrast-enhanced computed tomographic (CT) images are used to provide the local tumor cell densities. We also incorporate the displacements derived from post-contrast CT images to account for the pancreatic motion. Experiments were performed on synthetic and clinical data to compare the differences between using different models of mass effect and between with and without imaged-derived motion.
Fig. 1.
Multiplicative growth decomposition. The original configuration  comprises the tumor (cyan) and its surrounding tissues (blue) before growth. The growth deformation gradient
comprises the tumor (cyan) and its surrounding tissues (blue) before growth. The growth deformation gradient 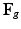 , which grows the tumor only, leads to an intermediate incompatible configuration
, which grows the tumor only, leads to an intermediate incompatible configuration 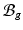 . With the elastic deformation gradient
. With the elastic deformation gradient 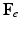 applied, the final configuration
applied, the final configuration 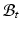 is compatible (Color figure online).
is compatible (Color figure online).
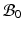 comprises the tumor (cyan) and its surrounding tissues (blue) before growth. The growth deformation gradient
comprises the tumor (cyan) and its surrounding tissues (blue) before growth. The growth deformation gradient 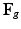 , which grows the tumor only, leads to an intermediate incompatible configuration
, which grows the tumor only, leads to an intermediate incompatible configuration 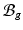 . With the elastic deformation gradient
. With the elastic deformation gradient 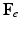 applied, the final configuration
applied, the final configuration 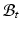 is compatible (Color figure online).
is compatible (Color figure online).2 Multiplicative Growth with Hyperelastic Mechanical Model
Let 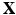 be the coordinates in the original configuration (
be the coordinates in the original configuration (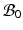 ) and
) and 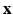 be the corresponding coordinates in the final (deformed) configuration (
be the corresponding coordinates in the final (deformed) configuration (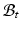 ) (Fig. 1). To model mass growth, the deformation gradient
) (Fig. 1). To model mass growth, the deformation gradient 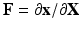 , which maps the original configuration to the final configuration as
, which maps the original configuration to the final configuration as 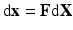 , can be decomposed into its elastic part (
, can be decomposed into its elastic part (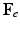 ) and growth part (
) and growth part (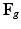 ) as
) as 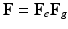 [11]. Inhomogeneous growth can result in gaps or overlaps in the intermediate configuration (
[11]. Inhomogeneous growth can result in gaps or overlaps in the intermediate configuration (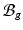 ), and the system equation cannot be solved therein. Therefore, we need to reformulate the quantities in
), and the system equation cannot be solved therein. Therefore, we need to reformulate the quantities in 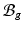 in terms of those in the compatible configuration
in terms of those in the compatible configuration 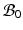 for the total-Lagrangian formulation [2].
for the total-Lagrangian formulation [2].
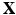 be the coordinates in the original configuration (
be the coordinates in the original configuration (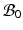 ) and
) and 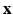 be the corresponding coordinates in the final (deformed) configuration (
be the corresponding coordinates in the final (deformed) configuration (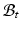 ) (Fig. 1). To model mass growth, the deformation gradient
) (Fig. 1). To model mass growth, the deformation gradient 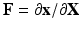 , which maps the original configuration to the final configuration as
, which maps the original configuration to the final configuration as 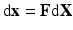 , can be decomposed into its elastic part (
, can be decomposed into its elastic part (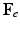 ) and growth part (
) and growth part (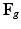 ) as
) as 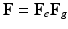 [11]. Inhomogeneous growth can result in gaps or overlaps in the intermediate configuration (
[11]. Inhomogeneous growth can result in gaps or overlaps in the intermediate configuration (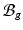 ), and the system equation cannot be solved therein. Therefore, we need to reformulate the quantities in
), and the system equation cannot be solved therein. Therefore, we need to reformulate the quantities in 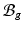 in terms of those in the compatible configuration
in terms of those in the compatible configuration 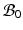 for the total-Lagrangian formulation [2].
for the total-Lagrangian formulation [2].In multiplicative growth decomposition, the elastic part is governed by the strain energy function which provides the stress-strain relation. The Green-Lagrange strain tensor 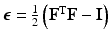 and its elastic part (
and its elastic part (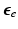 ) and growth part (
) and growth part (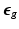 ) are related as:
) are related as:
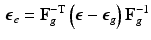
With tissue growth, the changes of mass and density need to be considered for accurate stress-strain relation. Let 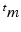 be the grown mass in
be the grown mass in 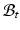 , and
, and 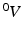 and
and 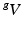 be the volumes in
be the volumes in 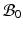 and
and 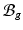 , respectively1. The densities of the grown mass with respect to different configurations are given as
, respectively1. The densities of the grown mass with respect to different configurations are given as 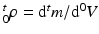 and
and 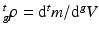 , with relation
, with relation 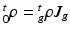 (
(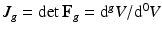 indicates the volume ratio). Therefore, the second Piola-Kirchhoff (PKII) stress tensor in
indicates the volume ratio). Therefore, the second Piola-Kirchhoff (PKII) stress tensor in 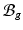 is given as:
is given as:
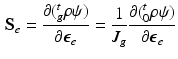
where 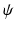 is the strain energy per unit grown mass, and thus
is the strain energy per unit grown mass, and thus 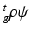 and
and 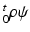 are the strain energy per unit intermediate and original volume, respectively. Thus the PKII stress tensor in
are the strain energy per unit intermediate and original volume, respectively. Thus the PKII stress tensor in 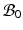 is given as:
is given as:
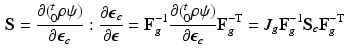
and the corresponding fourth-order elasticity tensor is given as:
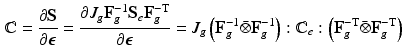
with the non-standard dyadic product ![$$\left[ \mathbf{A}\bar{\otimes }\mathbf{B}\right] _{ijkl} = \left[ \mathbf{A}\right] _{ik} \left[ \mathbf{B}\right] _{jl}$$](/wp-content/uploads/2016/09/A339424_1_En_39_Chapter_IEq42.gif) and
and 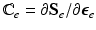 . Note that when there is no growth (i.e.
. Note that when there is no growth (i.e. 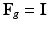 ),
), 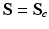 and
and 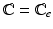 .
.
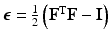 and its elastic part (
and its elastic part (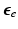 ) and growth part (
) and growth part (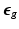 ) are related as:
) are related as: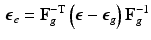
(1)
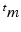 be the grown mass in
be the grown mass in 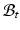 , and
, and 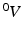 and
and 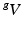 be the volumes in
be the volumes in 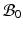 and
and 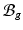 , respectively1. The densities of the grown mass with respect to different configurations are given as
, respectively1. The densities of the grown mass with respect to different configurations are given as 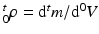 and
and 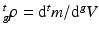 , with relation
, with relation 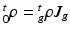 (
(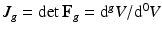 indicates the volume ratio). Therefore, the second Piola-Kirchhoff (PKII) stress tensor in
indicates the volume ratio). Therefore, the second Piola-Kirchhoff (PKII) stress tensor in 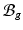 is given as:
is given as: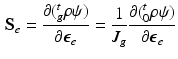
(2)
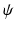 is the strain energy per unit grown mass, and thus
is the strain energy per unit grown mass, and thus 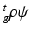 and
and 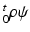 are the strain energy per unit intermediate and original volume, respectively. Thus the PKII stress tensor in
are the strain energy per unit intermediate and original volume, respectively. Thus the PKII stress tensor in 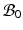 is given as:
is given as: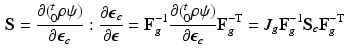
(3)
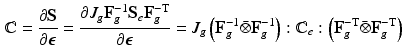
(4)
![$$\left[ \mathbf{A}\bar{\otimes }\mathbf{B}\right] _{ijkl} = \left[ \mathbf{A}\right] _{ik} \left[ \mathbf{B}\right] _{jl}$$](/wp-content/uploads/2016/09/A339424_1_En_39_Chapter_IEq42.gif) and
and 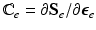 . Note that when there is no growth (i.e.
. Note that when there is no growth (i.e. 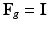 ),
), 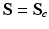 and
and 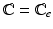 .
.To model the highly deformable pancreas, the modified Saint-Venant-Kirchhoff (hyperelastic) constitutive law is used [8]:
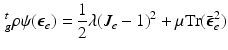
where 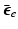 is the isovolumetric part of
is the isovolumetric part of 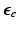 and
and 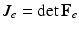 . The first and second term of (5) account for the volumetric and isochoric elastic response, respectively, and thus
. The first and second term of (5) account for the volumetric and isochoric elastic response, respectively, and thus 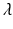 is the bulk modulus and
is the bulk modulus and 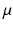 is the shear modulus.
is the shear modulus.
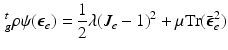
(5)
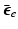 is the isovolumetric part of
is the isovolumetric part of 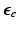 and
and 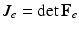 . The first and second term of (5) account for the volumetric and isochoric elastic response, respectively, and thus
. The first and second term of (5) account for the volumetric and isochoric elastic response, respectively, and thus 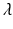 is the bulk modulus and
is the bulk modulus and 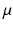 is the shear modulus.
is the shear modulus.Therefore, given 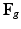 from a growth model, and
from a growth model, and 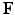 the existing deformation,
the existing deformation, 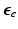 can be computed by (1).
can be computed by (1). 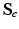 and
and 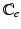 can then be computed using (5) and converted to
can then be computed using (5) and converted to 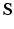 and
and 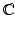 by (3) and (4) for the total-Lagrangian formulation. The system is solved by FEM with Newton-Raphson iterations for the final geometry [2].
by (3) and (4) for the total-Lagrangian formulation. The system is solved by FEM with Newton-Raphson iterations for the final geometry [2].
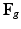 from a growth model, and
from a growth model, and 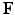 the existing deformation,
the existing deformation, 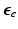 can be computed by (1).
can be computed by (1). 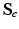 and
and 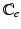 can then be computed using (5) and converted to
can then be computed using (5) and converted to 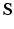 and
and 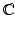 by (3) and (4) for the total-Lagrangian formulation. The system is solved by FEM with Newton-Raphson iterations for the final geometry [2].
by (3) and (4) for the total-Lagrangian formulation. The system is solved by FEM with Newton-Raphson iterations for the final geometry [2].2.1 Orthotropic Growth
The growth deformation 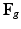 can be modeled using explicit functions. Although tissue structure is unavailable in our data, orthotropic mass growth is adopted [11]:
can be modeled using explicit functions. Although tissue structure is unavailable in our data, orthotropic mass growth is adopted [11]:
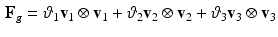
with 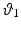 ,
, 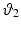 , and
, and 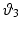 the stretch ratios along the orthonormal vectors
the stretch ratios along the orthonormal vectors 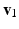 ,
, 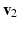 , and
, and 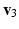 , respectively. All
, respectively. All 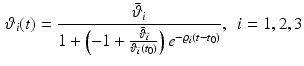
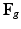 can be modeled using explicit functions. Although tissue structure is unavailable in our data, orthotropic mass growth is adopted [11]:
can be modeled using explicit functions. Although tissue structure is unavailable in our data, orthotropic mass growth is adopted [11]: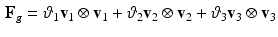
(6)
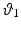 ,
, 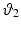 , and
, and 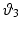 the stretch ratios along the orthonormal vectors
the stretch ratios along the orthonormal vectors 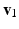 ,
, 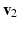 , and
, and 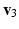 , respectively. All
, respectively. All 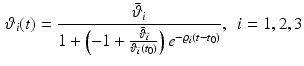
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree




