(1)
Faculty of Medicine, Department, of Oncology and Medical Physics Unit, McGill University, Montreal, Québec, Canada
Abstract
Chapter 5 consists of 10 problems covering two-particle collisions in 3 sections. Two particle collisions are well known in nuclear physics and radiation dosimetry. Typically, these collisions are characterized by an energetic projectile striking a stationary target and resulting in the most general case in an intermediate compound that subsequently decays into two reaction products.
Three categories of charged particles are considered as projectile: (1) light charged particles such as electron and positron, (2) heavy charged particle, such as proton and alpha particle, and (3) neutral particle, such as neutron. The possible targets are: (1) atoms as a whole, (2) atomic nuclei, and (3) atomic orbital electrons. The collisions are classified into three categories: (1) nuclear reactions, (2) elastic collisions, and (3) inelastic collisions.
The many types of interacting particles as well as the various possible categories of interactions result in a wide range of two-particle collisions of interest in nuclear physics and medical physics.
Problems in Sect. 5.1 deal with general aspects of two-particle collisions in classical physics, while Sect. 5.2 introduces nuclear reactions and addresses issues related to reaction Q value and threshold energy. Section 5.2 also deals with the relationship between reaction Q value and threshold energy and addresses the relationship between the two as well as the various methods to determine Q value, such as the atomic rest energy method, the nuclear rest energy method, and the binding energy method.
Section 5.3 concentrates on elastic two-particle collisions and energy transfer from the projectile to the target in this type of collision covering the general energy transfer as well as maximum energy transfer using classical and relativistic physics.
Chapter 5 consists of 10 problems covering two-particle collisions in 3 sections. Two particle collisions are well known in nuclear physics and radiation dosimetry. Typically, these collisions are characterized by an energetic projectile striking a stationary target and resulting in the most general case in an intermediate compound that subsequently decays into two reaction products.
Three categories of charged particles are considered as projectile: (1) light charged particles such as electron and positron, (2) heavy charged particle, such as proton and alpha particle, and (3) neutral particle, such as neutron. The possible targets are: (1) atoms as a whole, (2) atomic nuclei, and (3) atomic orbital electrons. The collisions are classified into three categories: (1) nuclear reactions, (2) elastic collisions, and (3) inelastic collisions.
The many types of interacting particles as well as the various possible categories of interactions result in a wide range of two-particle collisions of interest in nuclear physics and medical physics.
Problems in Sect. 5.1 deal with general aspects of two-particle collisions in classical physics, while Sect. 5.2 introduces nuclear reactions and addresses issues related to reaction Q value and threshold energy. Section 5.2 also deals with the relationship between reaction Q value and threshold energy and addresses the relationship between the two as well as the various methods to determine Q value, such as the atomic rest energy method, the nuclear rest energy method, and the binding energy method.
Section 5.3 concentrates on elastic two-particle collisions and energy transfer from the projectile to the target in this type of collision covering the general energy transfer as well as maximum energy transfer using classical and relativistic physics.
5.1 Collisions of Two Particles: General Aspects
5.1.Q1 (117)
An electron e of rest energy m e c 2=0.511 MeV collides head-on with a stationary hydrogen atom H of rest energy m H c 2≈m p c 2+m e c 2=938.272 MeV+0.511 MeV=938.783 MeV.
(a)
Determine the fraction of the incident electron kinetic energy 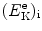 transferred as kinetic energy
transferred as kinetic energy 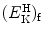 to the hydrogen atom, assuming that the collision is elastic.
to the hydrogen atom, assuming that the collision is elastic.
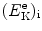 transferred as kinetic energy
transferred as kinetic energy 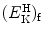 to the hydrogen atom, assuming that the collision is elastic.
to the hydrogen atom, assuming that the collision is elastic.(b)
Determine the minimum initial velocity 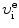 and minimum kinetic energy
and minimum kinetic energy 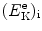 of the incident electron assuming that the collision is inelastic which means that the hydrogen atom, in addition to kinetic energy
of the incident electron assuming that the collision is inelastic which means that the hydrogen atom, in addition to kinetic energy 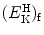 also acquires a characteristic energy E ∗ from the incident electron.
also acquires a characteristic energy E ∗ from the incident electron.
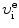 and minimum kinetic energy
and minimum kinetic energy 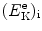 of the incident electron assuming that the collision is inelastic which means that the hydrogen atom, in addition to kinetic energy
of the incident electron assuming that the collision is inelastic which means that the hydrogen atom, in addition to kinetic energy 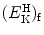 also acquires a characteristic energy E ∗ from the incident electron.
also acquires a characteristic energy E ∗ from the incident electron.SOLUTION:
(a) For elastic one-dimensional collision, in conjunction with classical mechanics and the following notation:
we consider conservation of momentum p and kinetic energy E K as follows
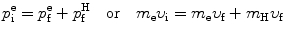
and
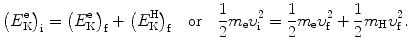
We solve (5.1) for υ f and insert the result υ f=υ i−(m H/m e)u f into (5.2) to get
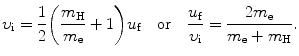
The fractional energy transfer 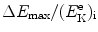 from the incident electron with kinetic energy
from the incident electron with kinetic energy 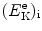 to hydrogen atom
to hydrogen atom 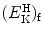 is now given as follows
is now given as follows
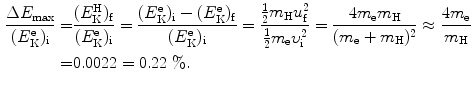
(b) In inelastic collision conservation of momentum remains the same as in elastic collision; however, the conservation of energy accounts also for the characteristic energy E ∗ that is transferred from the electron to hydrogen atom in addition to kinetic energy.
υ i and υ f are the initial and final velocities, respectively, of the electron
u i=0 and u f are the initial and final velocities, respectively, of the hydrogen atom,
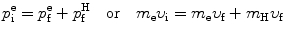
(5.1)
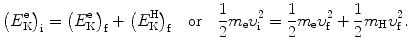
(5.2)
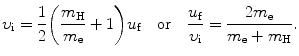
(5.3)
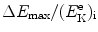 from the incident electron with kinetic energy
from the incident electron with kinetic energy 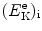 to hydrogen atom
to hydrogen atom 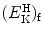 is now given as follows
is now given as follows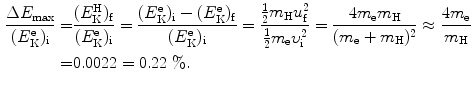
(5.4)
Conservation of momentum thus reads
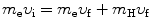
and conservation of energy
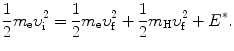
Again, we solve (5.5) for υ f and insert the result υ f=υ i−(m H/m e)u f into (5.6) to get the following quadratic equation for u f as a function of υ i and E ∗
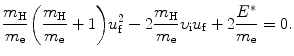
The two general solutions of (5.7) are
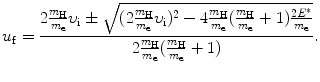
A physically meaningful solution to (5.7) requires that the radical in u f be real and we thus get the following inequality
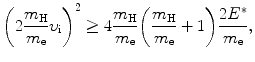
that gives the following result for the minimum required velocity (υ i)min and minimum required kinetic energy ![$[(E_{\mathrm{K}}^{\mathrm{e}})_{\mathrm{i}}]_{\min }$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_IEq9.gif) of the incident electron
of the incident electron
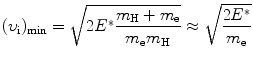
and
![$$ \bigl[\bigl(E_{\mathrm{K}}^{\mathrm{e}}\bigr)_{\mathrm{i}} \bigr]_{\min } = \frac{m_{\mathrm{e}}\upsilon _{\min }^{2}}{2} = E^{*} \biggl( 1 + \frac{m_{\mathrm{e}}}{m_{\mathrm{H}}} \biggr). $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ11.gif)
The result for the minimum kinetic energy of (5.11) indicates that the incident electron must possess a kinetic energy that exceeds slightly the characteristic energy E ∗.
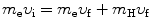
(5.5)
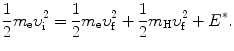
(5.6)
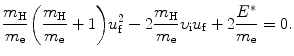
(5.7)
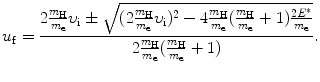
(5.8)
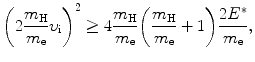
(5.9)
![$[(E_{\mathrm{K}}^{\mathrm{e}})_{\mathrm{i}}]_{\min }$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_IEq9.gif) of the incident electron
of the incident electron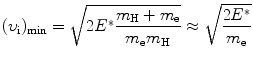
(5.10)
![$$ \bigl[\bigl(E_{\mathrm{K}}^{\mathrm{e}}\bigr)_{\mathrm{i}} \bigr]_{\min } = \frac{m_{\mathrm{e}}\upsilon _{\min }^{2}}{2} = E^{*} \biggl( 1 + \frac{m_{\mathrm{e}}}{m_{\mathrm{H}}} \biggr). $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ11.gif)
(5.11)
5.1.Q2 (118)
Two billiard balls of unknown masses m 1 and m 2 collide, with the projectile m 1 moving with velocity υ before collision and the target m 2 stationary before collision. After collision m 1 has a speed of 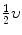 and moves at 90° to its original direction.
and moves at 90° to its original direction.
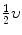 and moves at 90° to its original direction.
and moves at 90° to its original direction.(a)
Determine the direction of motion of billiard ball m 2 after the collision.
(b)
Determine the ratio m 1/m 2 between the masses of the two billiard balls.
(c)
Determine the velocity of billiard ball m 2 as a function of the incident velocity υ of billiard ball m 1.
(d)
Determine the energy transfer fraction from ball m 1 to ball m 2 in the collision.
SOLUTION:
A schematic diagram of the collision is presented in Fig. 5.1, with m 1 and m 2 the two billiard balls; the origin of the Cartesian coordinate system at the center of the stationary ball m 2 before collision; υ 1=υ the velocity of ball m 1 before collision; 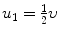 the velocity of ball m 1 after collision; υ 2=0 the velocity of ball m 2 before collision; u 2 the velocity of ball m 2 after collision;
the velocity of ball m 1 after collision; υ 2=0 the velocity of ball m 2 before collision; u 2 the velocity of ball m 2 after collision; 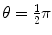 the scattering angle of the projectile; and ϕ the recoil angle of the target.
the scattering angle of the projectile; and ϕ the recoil angle of the target.
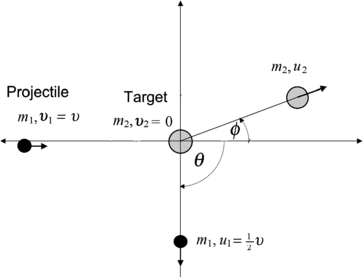
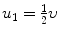 the velocity of ball m 1 after collision; υ 2=0 the velocity of ball m 2 before collision; u 2 the velocity of ball m 2 after collision;
the velocity of ball m 1 after collision; υ 2=0 the velocity of ball m 2 before collision; u 2 the velocity of ball m 2 after collision; 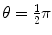 the scattering angle of the projectile; and ϕ the recoil angle of the target.
the scattering angle of the projectile; and ϕ the recoil angle of the target.
Fig. 5.1
Schematic diagram of the collision between billiard ball m 1 with billiard ball m 2. The projectile m 1 is scattered with scattering angle 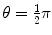 , the target m 2 recoils with angle ϕ
, the target m 2 recoils with angle ϕ
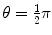 , the target m 2 recoils with angle ϕ
, the target m 2 recoils with angle ϕ Parameters of the collision process are evaluated using conservation of momentum p and kinetic energy E K as follows:
Conservation of momentum (x component):
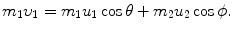
Conservation of momentum (y component):
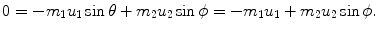
Conservation of kinetic energy
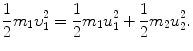
(a) Recoil angle ϕ will be determined from (5.12) and (5.13) for conservation of momentum as follows (note: scattering angle 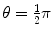 ). From (5.12) and (5.13) we get, respectively,
). From (5.12) and (5.13) we get, respectively,
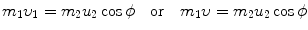
and
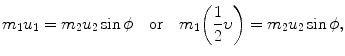
and from (5.15) and (5.16) it follows that 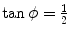 or ϕ=arctan0.5=26.57∘.
or ϕ=arctan0.5=26.57∘.
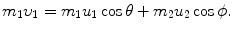
(5.12)
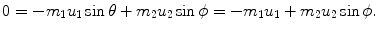
(5.13)
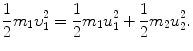
(5.14)
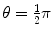 ). From (5.12) and (5.13) we get, respectively,
). From (5.12) and (5.13) we get, respectively,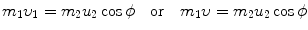
(5.15)
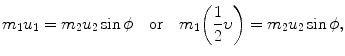
(5.16)
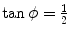 or ϕ=arctan0.5=26.57∘.
or ϕ=arctan0.5=26.57∘.(b) The ratio m 1/m 2 is calculated from the conservation of energy (5.14) in conjunction with (5.15) as follows
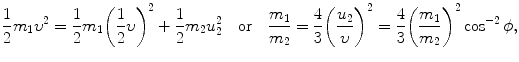
where we used (5.15) to obtain u 2/υ=m 1/(m 2cosϕ) and insert it into (5.17) to get ratio m 1/m 2
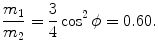
(c) Velocity u 2 as a function of incident velocity υ is easily determined from (5.15) and (5.18)
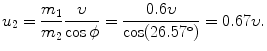
(d) Energy transfer fraction ΔE K/(E K)i where (E K)i is the initial kinetic energy of ball m 1 is given as
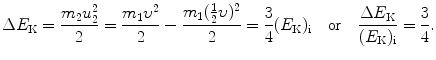
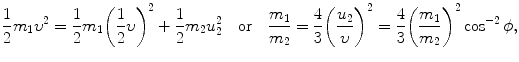
(5.17)
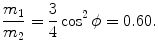
(5.18)
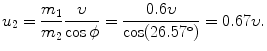
(5.19)
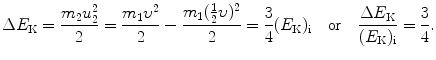
(5.20)
5.2 Nuclear Reactions
5.2.Q1 (119)
In 1932 Chadwick discovered the neutron by bombarding beryllium 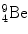 with α particles to produce neutron from the following nuclear reaction
with α particles to produce neutron from the following nuclear reaction
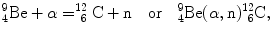
where reactants 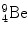 and α particle are the target and projectile, respectively, and
and α particle are the target and projectile, respectively, and 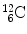 and n are reaction products carbon-12 and neutron, respectively. In general, reaction energy is referred to as Q value; positive (Q>0) in exothermic reaction and negative (Q<0) in endothermic reaction.
and n are reaction products carbon-12 and neutron, respectively. In general, reaction energy is referred to as Q value; positive (Q>0) in exothermic reaction and negative (Q<0) in endothermic reaction.
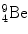 with α particles to produce neutron from the following nuclear reaction
with α particles to produce neutron from the following nuclear reaction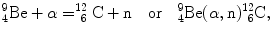
(5.21)
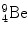 and α particle are the target and projectile, respectively, and
and α particle are the target and projectile, respectively, and 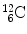 and n are reaction products carbon-12 and neutron, respectively. In general, reaction energy is referred to as Q value; positive (Q>0) in exothermic reaction and negative (Q<0) in endothermic reaction.
and n are reaction products carbon-12 and neutron, respectively. In general, reaction energy is referred to as Q value; positive (Q>0) in exothermic reaction and negative (Q<0) in endothermic reaction.(a)
State three methods that can be used in calculation of Q value of a nuclear reaction.
(b)
Determine Q value of the Chadwick nuclear reaction used in discovery of the neutron.
(c)
Is the Chadwick reaction exothermic or endothermic? If it is exothermic, can the reaction occur spontaneously or at very low kinetic energy of α particle?
SOLUTION:
Figure 5.2 shows a schematic diagram of a binary nuclear reaction characterized as a two-particle collision of a projectile with rest mass M 1, velocity υ 1, momentum p 1, and kinetic energy (E K)1 striking a stationary target with mass M 2 and velocity υ 2=0. An intermediate compound nucleus is produced temporarily and it decays into two reaction products, one of mass M 3 ejected with velocity υ 3 at an angle ϕ to the incident projectile direction, and the other of mass M 4 ejected with velocity υ 4 at an angle θ to the incident projectile direction of motion.
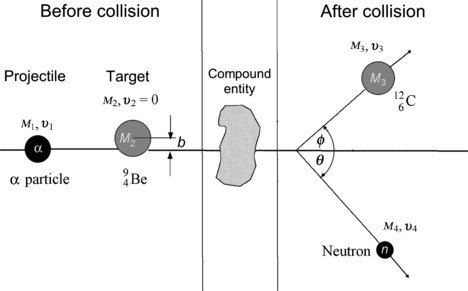

Fig. 5.2
Schematic diagram of a two-particle collision evolving into a nuclear reaction
(a) In any nuclear reaction the sum of total energies before the reaction ∑ i,before E i must equal the sum of total energies after the reaction ∑ i,after E i , or
![$$ \sum_{i, \mathrm{before}} E_{i} = \sum _{i, \mathrm{after}} E_{i} \equiv \sum _{i} \bigl[(E_{\mathrm{K}})_{i} + M_{i}c^{2}\bigr] = \sum_{i} \bigl[(E_{\mathrm{K}})_{i} + M_{i}c^{2}\bigr]. $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ22.gif)
Any change in the sum of kinetic energies before and after the reaction is compensated by an equivalent change in the sum of rest energies before and after the reaction or an equivalent change in the sum of binding energies before and after the reaction. The so-called Q value of a nuclear reaction is used to quantify the change in kinetic energy.
![$$ \sum_{i, \mathrm{before}} E_{i} = \sum _{i, \mathrm{after}} E_{i} \equiv \sum _{i} \bigl[(E_{\mathrm{K}})_{i} + M_{i}c^{2}\bigr] = \sum_{i} \bigl[(E_{\mathrm{K}})_{i} + M_{i}c^{2}\bigr]. $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ22.gif)
(5.22)
Three methods for calculation of Q value of binary nuclear reactions are:
(1) Kinetic energy method: Subtract the kinetic energy of the reactants (projectile and target) before the reaction ∑ i,before(E K) i from the sum of kinetic energies of the reaction products after the reaction ∑ i,after(E K) i , or
![$$ Q = \sum_{i, \mathrm{after}} (E_{\mathrm{K}})_{i} - \sum_{i, \mathrm{before}} (E_{\mathrm{K}})_{i} = \bigl[(E_{\mathrm{K}})_{3} + (E_{\mathrm{K}})_{4}\bigr] - \bigl[(E_{\mathrm{K}})_{1} + (E_{\mathrm{K}})_{2} \bigr]. $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ23.gif)
(2) Rest energy method: Subtract the sum of nuclear rest energies of the reaction products after the reaction ∑ i,before M i c 2 from the sum of rest energies of reactants (projectile and target) before the reaction ∑ i,after M i c 2, or
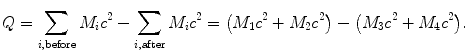
Note that in (5.24) M stands for nuclear mass. If atomic masses 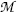 rather than nuclear masses are used in calculations of Q values for nuclear reactions, in many instances the electron masses cancel out, so that there is no difference in the Q value result. However, in situations where electron masses do not cancel out, special care must be taken when using atomic masses to account for all electrons involved in the interaction.
rather than nuclear masses are used in calculations of Q values for nuclear reactions, in many instances the electron masses cancel out, so that there is no difference in the Q value result. However, in situations where electron masses do not cancel out, special care must be taken when using atomic masses to account for all electrons involved in the interaction.
![$$ Q = \sum_{i, \mathrm{after}} (E_{\mathrm{K}})_{i} - \sum_{i, \mathrm{before}} (E_{\mathrm{K}})_{i} = \bigl[(E_{\mathrm{K}})_{3} + (E_{\mathrm{K}})_{4}\bigr] - \bigl[(E_{\mathrm{K}})_{1} + (E_{\mathrm{K}})_{2} \bigr]. $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ23.gif)
(5.23)
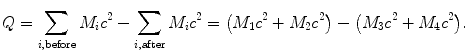
(5.24)
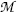 rather than nuclear masses are used in calculations of Q values for nuclear reactions, in many instances the electron masses cancel out, so that there is no difference in the Q value result. However, in situations where electron masses do not cancel out, special care must be taken when using atomic masses to account for all electrons involved in the interaction.
rather than nuclear masses are used in calculations of Q values for nuclear reactions, in many instances the electron masses cancel out, so that there is no difference in the Q value result. However, in situations where electron masses do not cancel out, special care must be taken when using atomic masses to account for all electrons involved in the interaction.(3) Binding energy method: Subtract the sum of total binding energies of reactants (projectile and target) before the reaction ∑ i,before(E B) i from the sum of total binding energies of reaction products after the reaction ∑ i,after(E B) i , or
![$$ Q = \sum_{i, \mathrm{after}} (E_{\mathrm{B}} )_{i} - \sum_{i, \mathrm{before}} (E_{\mathrm{B}} )_{i} = \bigl[(E_{\mathrm{B}})_{3} + (E_{\mathrm{B}})_{4}\bigr] - \bigl[(E_{\mathrm{B}})_{1} + (E_{\mathrm{B}})_{2} \bigr]. $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ25.gif)
(b) Q value of the Chadwick nuclear reaction 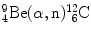 is calculated with the nuclear rest energy method as well as with the binding energy method, both described in (a). The results are summarized as follows:
is calculated with the nuclear rest energy method as well as with the binding energy method, both described in (a). The results are summarized as follows:
Q value calculated with the rest energy method is
![$$\begin{aligned} Q =& \sum_{i, \mathrm{before}} M_{i}c^{2} - \sum_{i, \mathrm{after}} M_{i}c^{2} = \bigl[m_{\alpha} c^{2} + M \bigl({}_{4}^{9}\mathrm{Be}\bigr)c^{2}\bigr] - \bigl[M\bigl(^{12}_{\phantom{1}6}\mathrm{C}\bigr)c^{2} + m_{\mathrm{n}}c^{2}\bigr] \\ =& 12 120.1290\ \mathrm{MeV} - 12\ 114.4278\ \mathrm{MeV} = 5.701\ \mathrm{MeV} \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ26.gif)
and with the binding energy method the result is the same, as expected
![$$\begin{aligned} Q =& \sum_{i, \mathrm{after}} (E_{\mathrm{B}} )_{i} - \sum_{i, \mathrm{before}} (E_{\mathrm{B}} )_{i} = \bigl[E_{\mathrm{B}}\bigl(^{12}_{\phantom{1}6}\mathrm{C}\bigr) + E_{\mathrm{B}}(\mathrm{n})\bigr] - \bigl[E_{\mathrm{B}}( \alpha ) + E_{\mathrm{B}}\bigl({}_{4}^{9}\mathrm{Be}\bigr) \bigr] \\ =& [92.16175 + 0]\ \mathrm{MeV} - [28.29569 + 58.16497]\ \mathrm{MeV} = 5.701\ \mathrm{MeV}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ27.gif)
(c) The Chadwick nuclear reaction is exothermic with Q value of 5.7 MeV and thus, in principle, should occur spontaneously and release 5.7 MeV of energy irrespective of the kinetic energy of the incident α particle. However, the reaction cannot occur spontaneously or with low energy α particles because of the nuclear potential barrier that an α particle must overcome when it strikes a positively-charged target nucleus.
![$$ Q = \sum_{i, \mathrm{after}} (E_{\mathrm{B}} )_{i} - \sum_{i, \mathrm{before}} (E_{\mathrm{B}} )_{i} = \bigl[(E_{\mathrm{B}})_{3} + (E_{\mathrm{B}})_{4}\bigr] - \bigl[(E_{\mathrm{B}})_{1} + (E_{\mathrm{B}})_{2} \bigr]. $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ25.gif)
(5.25)
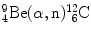 is calculated with the nuclear rest energy method as well as with the binding energy method, both described in (a). The results are summarized as follows:
is calculated with the nuclear rest energy method as well as with the binding energy method, both described in (a). The results are summarized as follows:Table 5.1
Summary of characteristics of the Chadwick 1932 neutron-discovery reaction
1 | Nuclear rest energy (MeV) | Binding energy (MeV) | |||
|---|---|---|---|---|---|
2 | Projectile | m 1 | α | 3 727.3791 | 28.29569 |
3 | Target | m 2 | 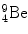 | 8 392.7499 | 58.16497 |
4 | ∑ i,before | 12 120.1290 | 86.46066 | ||
5 | Reaction product | m 3 | 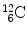 | 11 174.8625 | 92.16175 |
6 | Reaction product | m 4 | n | 939.5653 | 0 |
7 | ∑ i,after | 12 114.4278 | 92.16175 |
![$$\begin{aligned} Q =& \sum_{i, \mathrm{before}} M_{i}c^{2} - \sum_{i, \mathrm{after}} M_{i}c^{2} = \bigl[m_{\alpha} c^{2} + M \bigl({}_{4}^{9}\mathrm{Be}\bigr)c^{2}\bigr] - \bigl[M\bigl(^{12}_{\phantom{1}6}\mathrm{C}\bigr)c^{2} + m_{\mathrm{n}}c^{2}\bigr] \\ =& 12 120.1290\ \mathrm{MeV} - 12\ 114.4278\ \mathrm{MeV} = 5.701\ \mathrm{MeV} \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ26.gif)
(5.26)
![$$\begin{aligned} Q =& \sum_{i, \mathrm{after}} (E_{\mathrm{B}} )_{i} - \sum_{i, \mathrm{before}} (E_{\mathrm{B}} )_{i} = \bigl[E_{\mathrm{B}}\bigl(^{12}_{\phantom{1}6}\mathrm{C}\bigr) + E_{\mathrm{B}}(\mathrm{n})\bigr] - \bigl[E_{\mathrm{B}}( \alpha ) + E_{\mathrm{B}}\bigl({}_{4}^{9}\mathrm{Be}\bigr) \bigr] \\ =& [92.16175 + 0]\ \mathrm{MeV} - [28.29569 + 58.16497]\ \mathrm{MeV} = 5.701\ \mathrm{MeV}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ27.gif)
(5.27)
5.2.Q2 (120)
In Prob. 119 the Chadwick nuclear reaction 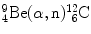 was shown to be exothermic with Q value of +5.7 MeV. This suggests that the inverse Chadwick reaction
was shown to be exothermic with Q value of +5.7 MeV. This suggests that the inverse Chadwick reaction 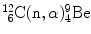 is endothermic with Q value of −5.7 MeV and thus can occur only when the incident neutron possesses kinetic energy that is equal to or exceeds a threshold kinetic energy
is endothermic with Q value of −5.7 MeV and thus can occur only when the incident neutron possesses kinetic energy that is equal to or exceeds a threshold kinetic energy 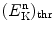 .
.
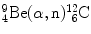 was shown to be exothermic with Q value of +5.7 MeV. This suggests that the inverse Chadwick reaction
was shown to be exothermic with Q value of +5.7 MeV. This suggests that the inverse Chadwick reaction 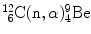 is endothermic with Q value of −5.7 MeV and thus can occur only when the incident neutron possesses kinetic energy that is equal to or exceeds a threshold kinetic energy
is endothermic with Q value of −5.7 MeV and thus can occur only when the incident neutron possesses kinetic energy that is equal to or exceeds a threshold kinetic energy 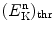 .
.(a)
Derive the general expression for threshold kinetic energy (E K)thr of an endothermic nuclear reaction.
(b)
Determine the relationship between threshold kinetic energy (E K)thr and Q value.
(c)
Determine neutron threshold kinetic energy 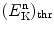 for the inverse Chadwick reaction.
for the inverse Chadwick reaction.
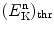 for the inverse Chadwick reaction.
for the inverse Chadwick reaction.SOLUTION:
(a) Threshold kinetic energy (E K)thr of an endothermic nuclear reaction is determined through the use of the so-called invariant E 2−p 2 c 2=inv applied to reactants (projectile and target) before the collision (in laboratory coordinate system) and to reaction products after the collision (in center-of-mass coordinate system), with
Total energy and momentum before collision (in laboratory coordinate system):
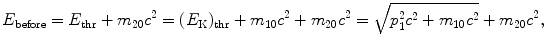
where E thr is the total threshold energy of the projectile, (E K)thr is the kinetic energy of the projectile, and p 1=p before is the momentum of the projectile, all given for before the collision and related through the standard relativistic expressions 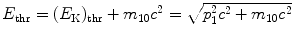 .
.
E
total energy of the system either before or after collision.
p
total momentum of the system either before or after collision.
c
speed of light in vacuum.
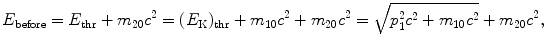
(5.28)
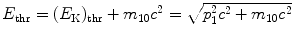 .
.Total energy and momentum after collision (in center-of-mass coordinate system)
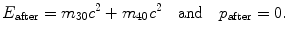
The invariant can now be expressed as follows:
![$$ \begin{aligned}[b] E^{2} - p^{2}c^{2} &= E_{\mathrm{before}}^{2} - p_{\mathrm{before}}^{2}c^{2} \equiv \bigl(\sqrt{p_{1}^{2}c^{2} + m_{10}c^{2}} + m_{20}c^{2} \bigr)^{2} - p_{1}^{2}c^{2} \\ &= E_{\mathrm{after}}^{2} - p_{\mathrm{after}}^{2}c^{2} \equiv \bigl(m_{30}c^{2} + m_{40}c^{2} \bigr)^{2} - 0, \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ30.gif)
resulting in total threshold energy E thr expressed as follows
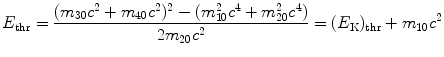
and threshold kinetic energy (E K)thr
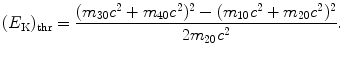
(b) Q value for a nuclear reaction is defined as
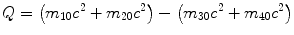
and can be expressed as follows
![$$\begin{aligned} \bigl(m_{30}c^{2} + m_{40}c^{2} \bigr)^{2} =& \bigl[\bigl(m_{10}c^{2} + m_{20}c^{2}\bigr) - Q\bigr]^{2} \\ =& \bigl(m_{10}c^{2} + m_{20}c^{2} \bigr)^{2} - 2Q\bigl(m_{10}c^{2} + m_{20}c^{2}\bigr) + Q^{2}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ34.gif)
Inserting (5.34) into (5.32) results in the following expression for (E K)thr in terms of Q
![$$ (E_{\mathrm{K}})_{\mathrm{thr}} = - Q \biggl[ \frac{m_{10}c^{2} + m_{20}c^{2}}{m_{20}c^{2}} + \frac{Q}{2m_{20}c^{2}} \biggr] \approx - Q \biggl[ 1 + \frac{m_{10}}{m_{20}} \biggr], $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ35.gif)
where we can generally ignore the term Q/(2m 20 c 2), since Q≪2m 20 c 2. In (5.35) the threshold kinetic energy of the projectile exceeds |Q| by a relatively small amount to account for the conservation of energy and momentum in the nuclear reaction.
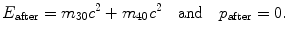
(5.29)
![$$ \begin{aligned}[b] E^{2} - p^{2}c^{2} &= E_{\mathrm{before}}^{2} - p_{\mathrm{before}}^{2}c^{2} \equiv \bigl(\sqrt{p_{1}^{2}c^{2} + m_{10}c^{2}} + m_{20}c^{2} \bigr)^{2} - p_{1}^{2}c^{2} \\ &= E_{\mathrm{after}}^{2} - p_{\mathrm{after}}^{2}c^{2} \equiv \bigl(m_{30}c^{2} + m_{40}c^{2} \bigr)^{2} - 0, \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ30.gif)
(5.30)
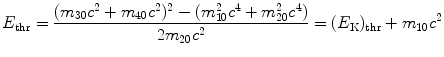
(5.31)
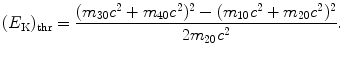
(5.32)
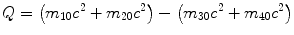
(5.33)
![$$\begin{aligned} \bigl(m_{30}c^{2} + m_{40}c^{2} \bigr)^{2} =& \bigl[\bigl(m_{10}c^{2} + m_{20}c^{2}\bigr) - Q\bigr]^{2} \\ =& \bigl(m_{10}c^{2} + m_{20}c^{2} \bigr)^{2} - 2Q\bigl(m_{10}c^{2} + m_{20}c^{2}\bigr) + Q^{2}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ34.gif)
(5.34)
![$$ (E_{\mathrm{K}})_{\mathrm{thr}} = - Q \biggl[ \frac{m_{10}c^{2} + m_{20}c^{2}}{m_{20}c^{2}} + \frac{Q}{2m_{20}c^{2}} \biggr] \approx - Q \biggl[ 1 + \frac{m_{10}}{m_{20}} \biggr], $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ35.gif)
(5.35)
(c) Q value for the inverse Chadwick nuclear reaction 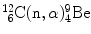 is determined either with the rest energy method or with the binding energy method
is determined either with the rest energy method or with the binding energy method
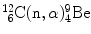 is determined either with the rest energy method or with the binding energy method
is determined either with the rest energy method or with the binding energy methodRest energy method:
![$$\begin{aligned} Q =& \bigl[m_{\mathrm{n}}c^{2} + M\bigl(^{12}_{\phantom{1}6}\mathrm{C}\bigr)c^{2}\bigr] - \bigl[m_{\alpha} c^{2} + M \bigl({}_{4}^{9}\mathrm{Be}\bigr)c^{2}\bigr] \\ =& [939.5653 + 11174.8625]\ \mathrm{MeV} - [3727.3791 + 8392.7499]\ \mathrm{MeV} \\ =& - 5.701\ \mathrm{MeV}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ36.gif)
Binding energy method:
![$$ \begin{aligned}[b] Q &= \bigl[E_{\mathrm{B}}\bigl({}_{2}^{4} \mathrm{He}\bigr) + E_{\mathrm{B}}\bigl({}_{4}^{9} \mathrm{Be}\bigr)\bigr] - \bigl[E_{\mathrm{B}}(\mathrm{n}) + E_{\mathrm{B}} \bigl(^{12}_{\phantom{1}6}\mathrm{C}\bigr)\bigr] \\ &= [28.29569 + 58.16497]\ \mathrm{MeV} - [0 + 92.16175] = - 5.70\ \mathrm{MeV}. \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ37.gif)
As shown in (5.35), the threshold kinetic energy of the neutron in the inverse Chadwick reaction is calculated as follows
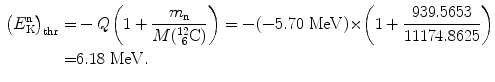
![$$\begin{aligned} Q =& \bigl[m_{\mathrm{n}}c^{2} + M\bigl(^{12}_{\phantom{1}6}\mathrm{C}\bigr)c^{2}\bigr] - \bigl[m_{\alpha} c^{2} + M \bigl({}_{4}^{9}\mathrm{Be}\bigr)c^{2}\bigr] \\ =& [939.5653 + 11174.8625]\ \mathrm{MeV} - [3727.3791 + 8392.7499]\ \mathrm{MeV} \\ =& - 5.701\ \mathrm{MeV}. \end{aligned}$$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ36.gif)
(5.36)
![$$ \begin{aligned}[b] Q &= \bigl[E_{\mathrm{B}}\bigl({}_{2}^{4} \mathrm{He}\bigr) + E_{\mathrm{B}}\bigl({}_{4}^{9} \mathrm{Be}\bigr)\bigr] - \bigl[E_{\mathrm{B}}(\mathrm{n}) + E_{\mathrm{B}} \bigl(^{12}_{\phantom{1}6}\mathrm{C}\bigr)\bigr] \\ &= [28.29569 + 58.16497]\ \mathrm{MeV} - [0 + 92.16175] = - 5.70\ \mathrm{MeV}. \end{aligned} $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ37.gif)
(5.37)
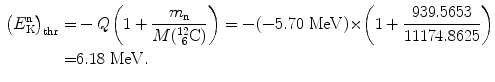
(5.38)
5.2.Q3 (121)
Consider the following three nuclear reactions:
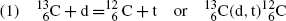
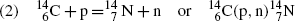
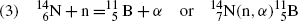
For each reaction determine:
Summarize results of (a), (b), (c), (d), and (e) in Table 5.2A.
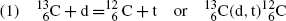
(5.39)
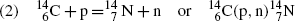
(5.40)
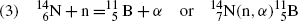
(5.41)
(a)
Q value.
(b)
Reaction type (exothermic or endothermic).
(c)
Threshold kinetic energy (E K)thr of the projectile.
(d)
Coulomb barrier energy E Coul.
(e)
Effective threshold energy (E K)min, i.e., minimum kinetic energy of the projectile required for the nuclear reaction to occur.
Table 5.2A
Summary of results for the three nuclear reactions of Prob. 121
Nuclear reaction | Reaction Q value (MeV) | Reaction type | Threshold energy (E K)thr (MeV) | Coulomb barrier E Coul (MeV) | Effective threshold (E K)min (MeV) | |
|---|---|---|---|---|---|---|
(1) | 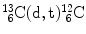 | |||||
(2) | 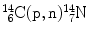 | |||||
(3) | 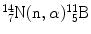 |
SOLUTION:
(a) Q value of a nuclear reaction m 1(m 2,m 3)m 4 is calculated either with the rest energy method
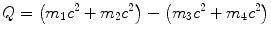
or with the binding energy method
![$$ Q=\bigl[E_{\mathrm{B}}(m_3) + E_{\mathrm{B}}(m_4) \bigr]-\bigl[E_{\mathrm{B}}(m_1) + E_{\mathrm{B}}(m_2) \bigr]. $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ43.gif)




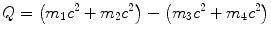
(5.42)
![$$ Q=\bigl[E_{\mathrm{B}}(m_3) + E_{\mathrm{B}}(m_4) \bigr]-\bigl[E_{\mathrm{B}}(m_1) + E_{\mathrm{B}}(m_2) \bigr]. $$](/wp-content/uploads/2016/04/A212719_1_En_5_Chapter_Equ43.gif)
(5.43)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree