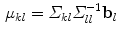Fig. 1
Examples of segmentations (in blue) obtained with local PDMs, showing suboptimal fitting in areas of complex geometry and high curvature on the spine (Color figure online)
Amongst existing techniques for vertebral image segmentation, statistical models of 3D shape [4] have been extensively used [2, 3, 5, 7, 8] due to their ability to build a shape prior from a representative training population. However, these methods consider at best a whole vertebra as the smallest unit for the construction of the point distribution models (PDMs). Due to the large variability of the vertebrae in particular at the processes and the generally small number of samples available for training, the obtained models are too constraining and not flexible enough to localize the fine details at areas of high curvatures.
In this paper, we present a new method for detailed modeling and segmentation of the vertebrae. The fundamental idea behind the proposed technique is to decompose each vertebra into a set of subparts based on their geometrical properties. By using a Vononoi [9] decomposition approach, we ensure that each of the main subparts of the vertebrae is well identified. With this approach, the shape constraints are effectively relaxed, allowing for an improved encoding of the fine details and shape variability at all the regions of the structures. Subsequently, in order to maintain the statistical coherence of the ensemble, conditional models are used to model the statistical inter-relationships between the different subparts. For shape reconstruction and segmentation, a robust model fitting procedure is introduced to exclude outlying inter-part relationships in the estimation of the shape parameters. The proposed technique is validated with a total of 30 spinal CT scans.
2 Method
The proposed framework consists of three main stages. Firstly, in Sect. 2.1, a subdivision of each vertebra into a number of subparts is proposed based on an approximate Voronoi region decomposition. Subsequently, the conditional models describing the statistical inter-relationships between the subparts are presented in Sect. 2.2. Finally, a model fitting approach based on all pair wise conditional models is introduced in Sect. 2.3, with the aim to estimate the shape parameters for each subpart robustly.
2.1 Vertebral Decomposition
Let us denote 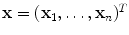 the landmark-based shape representation of each vertebra, where
the landmark-based shape representation of each vertebra, where 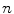 is the number of landmarks used to discretize the 3D shape. The aim of this section is to obtain a subdivision of
is the number of landmarks used to discretize the 3D shape. The aim of this section is to obtain a subdivision of 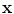 into
into 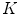 sub-components.
sub-components.
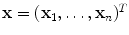 the landmark-based shape representation of each vertebra, where
the landmark-based shape representation of each vertebra, where 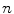 is the number of landmarks used to discretize the 3D shape. The aim of this section is to obtain a subdivision of
is the number of landmarks used to discretize the 3D shape. The aim of this section is to obtain a subdivision of 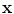 into
into 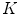 sub-components.
sub-components.We do this in this paper by using a polygon clustering algorithm described in [9], which provides a compact subdivision of the shape based on the concept of a Voronoi diagram [1]. Furthermore, let us denote 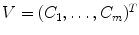 the triangulation of the shape
the triangulation of the shape 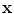 , where
, where 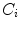 ,
, 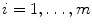 , represents each face on the mesh, and
, represents each face on the mesh, and 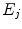 the set of edges between all adjacent triangles. Given the centroids
the set of edges between all adjacent triangles. Given the centroids 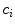 corresponding to each of the triangular triangles
corresponding to each of the triangular triangles 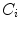 , the algorithm computes an approximation of a centroidal Voronoi diagram (CVD). The energy term to minimize is:
, the algorithm computes an approximation of a centroidal Voronoi diagram (CVD). The energy term to minimize is:
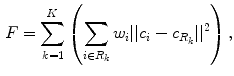
where 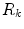 is a subset of
is a subset of 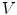 (i.e. subpart of the shape),
(i.e. subpart of the shape), 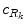 is the center of the region, and
is the center of the region, and 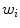 is the area of triangle
is the area of triangle 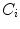 .
.
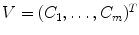 the triangulation of the shape
the triangulation of the shape 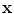 , where
, where 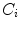 ,
, 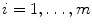 , represents each face on the mesh, and
, represents each face on the mesh, and 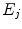 the set of edges between all adjacent triangles. Given the centroids
the set of edges between all adjacent triangles. Given the centroids 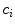 corresponding to each of the triangular triangles
corresponding to each of the triangular triangles 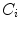 , the algorithm computes an approximation of a centroidal Voronoi diagram (CVD). The energy term to minimize is:
, the algorithm computes an approximation of a centroidal Voronoi diagram (CVD). The energy term to minimize is: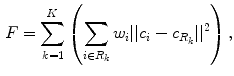
(1)
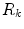 is a subset of
is a subset of 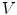 (i.e. subpart of the shape),
(i.e. subpart of the shape), 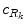 is the center of the region, and
is the center of the region, and 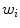 is the area of triangle
is the area of triangle 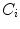 .
.To minimize Eq. 1, we use an iterative approach over the subset of edges 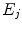 between adjacent regions. The regions
between adjacent regions. The regions 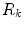 are initialized as a single triangle that is randomly chosen amongst
are initialized as a single triangle that is randomly chosen amongst 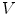 . The remaining triangles are assigned to the
. The remaining triangles are assigned to the 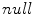 region
region 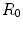 . We then iterate only over the edges that are between two regions
. We then iterate only over the edges that are between two regions 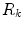 and
and 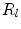 , or between any
, or between any 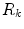 and
and 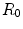 . Then we assign one of the two triangles adjacent to the current edge to the region that minimizes Eq. 1. At some point, the region
. Then we assign one of the two triangles adjacent to the current edge to the region that minimizes Eq. 1. At some point, the region 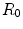 will become empty. The iterative algorithm will continue until no modification of the region assignments for the triangles lead to an improvement of the subdivision according to Eq. 1.
will become empty. The iterative algorithm will continue until no modification of the region assignments for the triangles lead to an improvement of the subdivision according to Eq. 1.
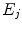 between adjacent regions. The regions
between adjacent regions. The regions 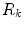 are initialized as a single triangle that is randomly chosen amongst
are initialized as a single triangle that is randomly chosen amongst 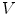 . The remaining triangles are assigned to the
. The remaining triangles are assigned to the 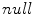 region
region 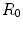 . We then iterate only over the edges that are between two regions
. We then iterate only over the edges that are between two regions 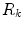 and
and 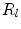 , or between any
, or between any 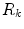 and
and 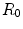 . Then we assign one of the two triangles adjacent to the current edge to the region that minimizes Eq. 1. At some point, the region
. Then we assign one of the two triangles adjacent to the current edge to the region that minimizes Eq. 1. At some point, the region 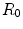 will become empty. The iterative algorithm will continue until no modification of the region assignments for the triangles lead to an improvement of the subdivision according to Eq. 1.
will become empty. The iterative algorithm will continue until no modification of the region assignments for the triangles lead to an improvement of the subdivision according to Eq. 1.Given that the regions of highest complexity and curvature on the vertebra are the different vertebral processes, we chose the lowest number of clusters 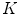 such that points selected roughly at the distal region of every process (transverse, superior/inferior articular and spinous) are assigned to a different region after the subdivision.
such that points selected roughly at the distal region of every process (transverse, superior/inferior articular and spinous) are assigned to a different region after the subdivision.
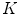 such that points selected roughly at the distal region of every process (transverse, superior/inferior articular and spinous) are assigned to a different region after the subdivision.
such that points selected roughly at the distal region of every process (transverse, superior/inferior articular and spinous) are assigned to a different region after the subdivision.Once the algorithm converges, all 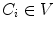 will belong to a unique region
will belong to a unique region 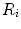 . However, the points that lie on the boundary edges between subparts will now belong to two adjacent regions. To resolve this ambiguity, we perform a last step where we go through the different regions sequentially and assign boundary points to the current region unless previously assigned.
. However, the points that lie on the boundary edges between subparts will now belong to two adjacent regions. To resolve this ambiguity, we perform a last step where we go through the different regions sequentially and assign boundary points to the current region unless previously assigned.
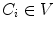 will belong to a unique region
will belong to a unique region 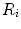 . However, the points that lie on the boundary edges between subparts will now belong to two adjacent regions. To resolve this ambiguity, we perform a last step where we go through the different regions sequentially and assign boundary points to the current region unless previously assigned.
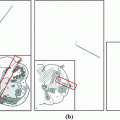
. However, the points that lie on the boundary edges between subparts will now belong to two adjacent regions. To resolve this ambiguity, we perform a last step where we go through the different regions sequentially and assign boundary points to the current region unless previously assigned.Figure 2 shows the obtained subdivision with 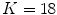 , where it can be seen that the main regions of high curvature now belong to a unique subpart.
, where it can be seen that the main regions of high curvature now belong to a unique subpart.
 , where it can be seen that the main regions of high curvature now belong to a unique subpart.
, where it can be seen that the main regions of high curvature now belong to a unique subpart.
Fig. 2
The obtained Voronoi decomposition with 18 subparts
2.2 Conditional Model Parametrization
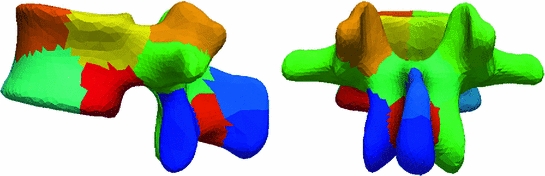
In the previous section we obtained  subcomponents
subcomponents 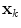 ,
, 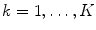 . The aim of this section is to describe the statistical modeling of the inter-part probability distributions, i.e.
. The aim of this section is to describe the statistical modeling of the inter-part probability distributions, i.e. 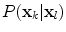 , where
, where 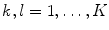 and
and 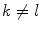 . More specifically, we would like to obtain new constraints for each part
. More specifically, we would like to obtain new constraints for each part 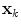 based on its conditional relationship with
based on its conditional relationship with 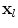 , that is, a new mean and covariance in the space of the shape parameters
, that is, a new mean and covariance in the space of the shape parameters 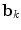 . Let us denote
. Let us denote 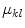 and
and 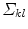 the values that form the new conditional constraints. In this paper, we choose to model
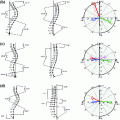
the values that form the new conditional constraints. In this paper, we choose to model  using a normal probability distribution. Thus, the mean and the covariance estimates are calculated as:
using a normal probability distribution. Thus, the mean and the covariance estimates are calculated as:
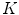 subcomponents
subcomponents 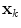 ,
, 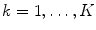 . The aim of this section is to describe the statistical modeling of the inter-part probability distributions, i.e.
. The aim of this section is to describe the statistical modeling of the inter-part probability distributions, i.e. 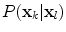 , where
, where 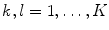 and
and 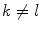 . More specifically, we would like to obtain new constraints for each part
. More specifically, we would like to obtain new constraints for each part 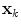 based on its conditional relationship with
based on its conditional relationship with 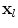 , that is, a new mean and covariance in the space of the shape parameters
, that is, a new mean and covariance in the space of the shape parameters 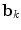 . Let us denote
. Let us denote 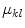 and
and 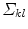 the values that form the new conditional constraints. In this paper, we choose to model
the values that form the new conditional constraints. In this paper, we choose to model  using a normal probability distribution. Thus, the mean and the covariance estimates are calculated as:
using a normal probability distribution. Thus, the mean and the covariance estimates are calculated as: