is given by:
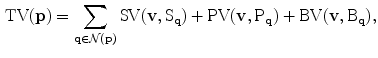
(1)
 represents each of the points in the neighborhood of
represents each of the points in the neighborhood of  and
and  are the stick, plate and ball tensor votes cast to
are the stick, plate and ball tensor votes cast to 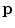 by every component of
by every component of 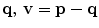 , and
, and 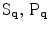 and
and 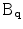 are the stick, plate and ball components of the tensor at
are the stick, plate and ball components of the tensor at 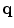 respectively. These components are given by:
respectively. These components are given by: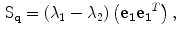
(2)
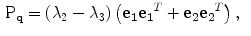
(3)
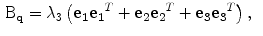
(4)
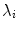 and
and 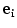 are the
are the 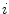 th largest eigenvalue and its corresponding eigenvector of the tensor at
th largest eigenvalue and its corresponding eigenvector of the tensor at 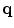 . Saliency measurements can be estimated from an analysis of the eigenvalues of the resulting tensors. Thus,
. Saliency measurements can be estimated from an analysis of the eigenvalues of the resulting tensors. Thus, 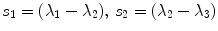 , and
, and 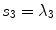 can be used as measurements of surfaceness, curveness and junctionness respectively.
can be used as measurements of surfaceness, curveness and junctionness respectively.
Fig. 1
Stick tensor voting. A stick  casts a stick vote
casts a stick vote 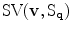 to
to  , which corresponds to the most likely tensorized normal at
, which corresponds to the most likely tensorized normal at 
 casts a stick vote
casts a stick vote 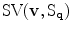 to
to 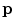 , which corresponds to the most likely tensorized normal at
, which corresponds to the most likely tensorized normal at 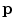
A stick tensor is a tensor with only a single eigenvalue greater than zero. Stick tensors are processed through the so-called stick tensor voting. The process is illustrated in Fig. 1. Given a known stick tensor 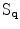 at
at 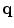 , the orientation of the vote cast by
, the orientation of the vote cast by 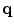 to
to 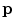 can be estimated by tensorizing the normal of a a circumference at
can be estimated by tensorizing the normal of a a circumference at 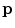 that joins
that joins 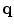 and
and 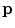 . This vote is then weighted by a decaying scalar function,
. This vote is then weighted by a decaying scalar function, 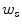 . The stick tensor vote is given by [20]:
. The stick tensor vote is given by [20]:
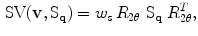
where 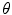 is shown in Fig. 1 and
is shown in Fig. 1 and 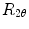 represents a rotation with respect to the axis
represents a rotation with respect to the axis 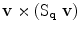 , which is perpendicular to the plane that contains
, which is perpendicular to the plane that contains 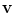 and
and 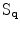 ; and
; and 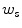 is an exponential decaying function that penalizes the arc-length
is an exponential decaying function that penalizes the arc-length 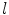 , and the curvature of the circumference,
, and the curvature of the circumference, 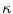 :
:
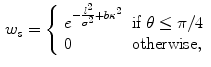
where 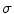 and
and 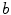 are parameters to weight the scale and the curvature respectively.
are parameters to weight the scale and the curvature respectively.
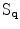 at
at 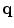 , the orientation of the vote cast by
, the orientation of the vote cast by 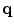 to
to 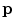 can be estimated by tensorizing the normal of a a circumference at
can be estimated by tensorizing the normal of a a circumference at 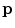 that joins
that joins 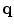 and
and 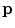 . This vote is then weighted by a decaying scalar function,
. This vote is then weighted by a decaying scalar function, 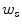 . The stick tensor vote is given by [20]:
. The stick tensor vote is given by [20]: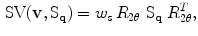
(5)
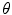 is shown in Fig. 1 and
is shown in Fig. 1 and 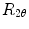 represents a rotation with respect to the axis
represents a rotation with respect to the axis 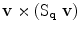 , which is perpendicular to the plane that contains
, which is perpendicular to the plane that contains 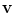 and
and 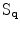 ; and
; and 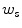 is an exponential decaying function that penalizes the arc-length
is an exponential decaying function that penalizes the arc-length 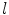 , and the curvature of the circumference,
, and the curvature of the circumference, 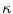 :
: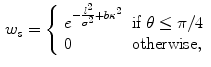
(6)
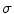 and
and 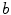 are parameters to weight the scale and the curvature respectively.
are parameters to weight the scale and the curvature respectively.In turn, a plate tensor is a tensor with 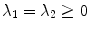 and
and 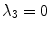 . Plate tensors are processed through the so-called plate tensor voting. The plate tensor voting uses the fact that any plate tensor
. Plate tensors are processed through the so-called plate tensor voting. The plate tensor voting uses the fact that any plate tensor 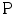 , can be decomposed into all possible stick tensors inside the plate. Let
, can be decomposed into all possible stick tensors inside the plate. Let 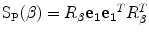 be a stick inside the plate
be a stick inside the plate 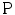 , with
, with 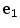 being its principal eigenvector, and
being its principal eigenvector, and 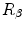 being a rotation with respect to an axis perpendicular to
being a rotation with respect to an axis perpendicular to 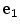 and
and 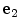 . Thus, the plate vote is defined as [20]:
. Thus, the plate vote is defined as [20]:
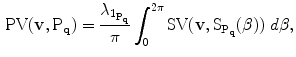
where 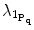 is the largest eigenvalue of
is the largest eigenvalue of 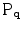 .
.
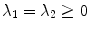 and
and 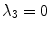 . Plate tensors are processed through the so-called plate tensor voting. The plate tensor voting uses the fact that any plate tensor
. Plate tensors are processed through the so-called plate tensor voting. The plate tensor voting uses the fact that any plate tensor  , can be decomposed into all possible stick tensors inside the plate. Let
, can be decomposed into all possible stick tensors inside the plate. Let  be a stick inside the plate
be a stick inside the plate 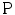 , with
, with 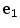 being its principal eigenvector, and
being its principal eigenvector, and 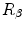 being a rotation with respect to an axis perpendicular to
being a rotation with respect to an axis perpendicular to 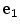 and
and 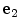 . Thus, the plate vote is defined as [20]:
. Thus, the plate vote is defined as [20]: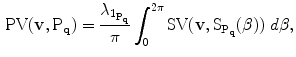
(7)
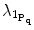 is the largest eigenvalue of
is the largest eigenvalue of 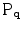 .
.Finally, a ball tensor is a tensor with 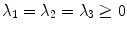 . The ball tensor voting is defined in a similar way as the plate tensor voting. Let
. The ball tensor voting is defined in a similar way as the plate tensor voting. Let 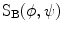 be a unitary stick tensor oriented in the direction
be a unitary stick tensor oriented in the direction 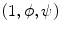 in spherical coordinates. Then, any ball tensor
in spherical coordinates. Then, any ball tensor 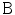 can be written as [20]:
can be written as [20]:
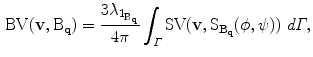
where 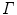 represents the surface of the unitary sphere, and
represents the surface of the unitary sphere, and 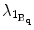 is the largest eigenvalue of
is the largest eigenvalue of 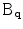 .
.
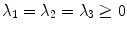 . The ball tensor voting is defined in a similar way as the plate tensor voting. Let
. The ball tensor voting is defined in a similar way as the plate tensor voting. Let 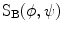 be a unitary stick tensor oriented in the direction
be a unitary stick tensor oriented in the direction 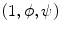 in spherical coordinates. Then, any ball tensor
in spherical coordinates. Then, any ball tensor 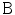 can be written as [20]:
can be written as [20]: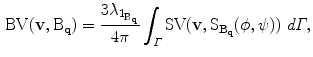
(8)
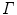 represents the surface of the unitary sphere, and
represents the surface of the unitary sphere, and 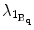 is the largest eigenvalue of
is the largest eigenvalue of 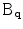 .
.2.2 Color Edge Detection Through the Classical Tensor Voting
In Ref. [21], we showed that the classical tensor voting and the well-known structure tensor [8] are closely related. These similarities were used in [21] to extend classical tensor voting to different types of images, especially color images. This extension can be used to extract edges. This subsection summarizes that method for gray-scale and color images.
2.2.1 Gray-Scale Images
Tensor voting can be adapted in order to robustly detect edges in gray-scale images by following three steps. First, the tensorized gradient, 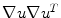 , is used to initialize a tensor at every pixel. Second, the stick tensor voting is applied in order to propagate the information encoded in the tensors. In this case, it is not necessary to apply the plate and ball voting processes since the plate and ball components are zero at every pixel. Thus, tensor voting is reduced to:
, is used to initialize a tensor at every pixel. Second, the stick tensor voting is applied in order to propagate the information encoded in the tensors. In this case, it is not necessary to apply the plate and ball voting processes since the plate and ball components are zero at every pixel. Thus, tensor voting is reduced to:
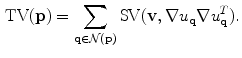
Finally, the resulting tensors are rescaled by the factor:
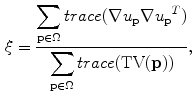
in order to renormalize the total energy of the tensorized gradient, where  refers to the given image.
refers to the given image.
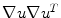 , is used to initialize a tensor at every pixel. Second, the stick tensor voting is applied in order to propagate the information encoded in the tensors. In this case, it is not necessary to apply the plate and ball voting processes since the plate and ball components are zero at every pixel. Thus, tensor voting is reduced to:
, is used to initialize a tensor at every pixel. Second, the stick tensor voting is applied in order to propagate the information encoded in the tensors. In this case, it is not necessary to apply the plate and ball voting processes since the plate and ball components are zero at every pixel. Thus, tensor voting is reduced to: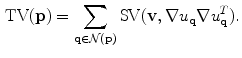
(9)
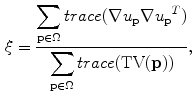
(10)
 refers to the given image.
refers to the given image.After having applied tensor voting and the energy normalization step, the principal eigenvalue 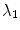 of the resulting tensors can be used to detect edges, since it attains high values not only at boundaries but also at corners.
of the resulting tensors can be used to detect edges, since it attains high values not only at boundaries but also at corners.
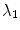 of the resulting tensors can be used to detect edges, since it attains high values not only at boundaries but also at corners.
of the resulting tensors can be used to detect edges, since it attains high values not only at boundaries but also at corners.2.2.2 Color Images
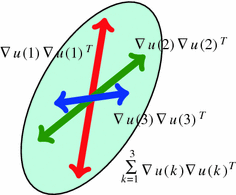
Figure 2 shows the two possible options to extend tensor voting to color images using the adaptation proposed in the previous subsection. The first option is to apply the stick tensor voting independently to every channel and then adding the individual results, that is:
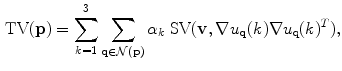
where 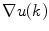 is the gradient at color channel
is the gradient at color channel 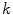 , and
, and 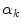 are weights used to give different relevance to every channel.
are weights used to give different relevance to every channel.
(11)
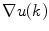 is the gradient at color channel
is the gradient at color channel 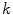 , and
, and 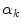 are weights used to give different relevance to every channel.
are weights used to give different relevance to every channel.
Fig. 2
Tensor voting can be applied to the color channels independently (the red, green and blue sticks) or to the sum of the tensorized gradients (the ellipse)
The second option is to apply (1) to the sum of tensorized gradients, with 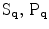 and
and 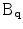 being the stick, plate and ball components of
being the stick, plate and ball components of 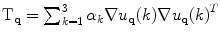 . For two-dimensional images, the computation of plate votes can be avoided since
. For two-dimensional images, the computation of plate votes can be avoided since 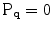 . Thus, the first option has the advantage that only the application of stick tensor voting is necessary, whereas the second option requires stick and ball tensor voting.
. Thus, the first option has the advantage that only the application of stick tensor voting is necessary, whereas the second option requires stick and ball tensor voting.
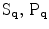 and
and 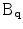 being the stick, plate and ball components of
being the stick, plate and ball components of 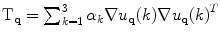 . For two-dimensional images, the computation of plate votes can be avoided since
. For two-dimensional images, the computation of plate votes can be avoided since 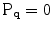 . Thus, the first option has the advantage that only the application of stick tensor voting is necessary, whereas the second option requires stick and ball tensor voting.
. Thus, the first option has the advantage that only the application of stick tensor voting is necessary, whereas the second option requires stick and ball tensor voting.In practice, both strategies are very similar since 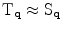 in most pixels of images of natural scenes [21]. Thus, in the experiments of Section 5, the first option has been used for the majority of pixels, whereas the second one only in those pixels in which the aforementioned approximation is not valid. In practice, the first option can be applied when the angle between any pair of gradients is below a threshold.
in most pixels of images of natural scenes [21]. Thus, in the experiments of Section 5, the first option has been used for the majority of pixels, whereas the second one only in those pixels in which the aforementioned approximation is not valid. In practice, the first option can be applied when the angle between any pair of gradients is below a threshold.
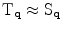 in most pixels of images of natural scenes [21]. Thus, in the experiments of Section 5, the first option has been used for the majority of pixels, whereas the second one only in those pixels in which the aforementioned approximation is not valid. In practice, the first option can be applied when the angle between any pair of gradients is below a threshold.
in most pixels of images of natural scenes [21]. Thus, in the experiments of Section 5, the first option has been used for the majority of pixels, whereas the second one only in those pixels in which the aforementioned approximation is not valid. In practice, the first option can be applied when the angle between any pair of gradients is below a threshold.Similarly to the case of gray-scale images, the classical tensor voting can be used to detect edges by means of the principal eigenvalue 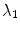 of the resulting tensor, after an energy normalization step similar to the one of (10).
of the resulting tensor, after an energy normalization step similar to the one of (10).
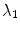 of the resulting tensor, after an energy normalization step similar to the one of (10).
of the resulting tensor, after an energy normalization step similar to the one of (10).Since this method does not apply any pre-processing step, its robustness must completely rely on the robustness of the classical tensor voting. This could not be sufficient in highly noisy scenarios. Thus, in order to improve the results it is necessary to iterate the method. By iterating tensor voting, the most significant edges can be reinforced at the expense of discarding small ridges. According to our experiments, a few iterations (two or three) usually give good results for both noisy and noiseless images.
3 Color Edge Detection Through an Adapted Tensor Voting
It is important to remark that tensor voting is a methodology in which information encoded through tensors is propagated and aggregated in a local neighborhood. Thus, it is possible to devise more appropriate methods for specific applications by tailoring the way in which tensors are encoded, propagated and aggregated, while maintaining the tensor voting spirit. In this line, we introduced a method for image denoising [17, 19] that can also be applied to robust color edge detection, since both problems can be tackled at the same time [18]. The next subsections detail the edge detector.
3.1 Encoding of Color Information
Before applying the proposed method, color is converted to the CIELAB space. Every CIELAB channel is then normalized to the range ![$$\left[ 0,\pi /2\right] $$](/wp-content/uploads/2016/03/A308467_1_En_9_Chapter_IEq68.gif) . In the first step of the method, the information of every pixel is encoded through three second-order 2D tensors, one for each normalized CIELAB color channel.
. In the first step of the method, the information of every pixel is encoded through three second-order 2D tensors, one for each normalized CIELAB color channel.
![$$\left[ 0,\pi /2\right] $$](/wp-content/uploads/2016/03/A308467_1_En_9_Chapter_IEq68.gif) . In the first step of the method, the information of every pixel is encoded through three second-order 2D tensors, one for each normalized CIELAB color channel.
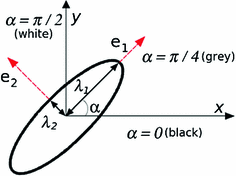
. In the first step of the method, the information of every pixel is encoded through three second-order 2D tensors, one for each normalized CIELAB color channel.Three perceptual measures are encoded in the tensors associated with every input pixel, namely: the normalized color at the pixel (in the specific channel), a measure of local uniformity (how edgeless its neighborhood is), and an estimation of edginess. Figure 3 shows the graphical interpretation of a tensor for channel 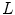 . The normalized color is encoded by the angle
. The normalized color is encoded by the angle 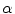 between the
between the 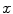 axis, which represents the lowest possible color value in the corresponding channel, and the eigenvector corresponding to the largest eigenvalue. For example, in channel
axis, which represents the lowest possible color value in the corresponding channel, and the eigenvector corresponding to the largest eigenvalue. For example, in channel 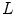 , a tensor with
, a tensor with 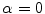 encodes black, whereas a tensor with
encodes black, whereas a tensor with 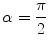 encodes white. In addition, local uniformity and edginess are encoded by means of the normalized
encodes white. In addition, local uniformity and edginess are encoded by means of the normalized 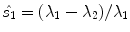 and
and 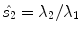 saliencies respectively. Thus, a pixel located at a completely uniform region is represented by means of three stick tensors, one for each color channel. In contrast, a pixel located at an ideal edge is represented by means of three ball tensors, one for every color channel.
saliencies respectively. Thus, a pixel located at a completely uniform region is represented by means of three stick tensors, one for each color channel. In contrast, a pixel located at an ideal edge is represented by means of three ball tensors, one for every color channel.
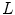 . The normalized color is encoded by the angle
. The normalized color is encoded by the angle 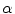 between the
between the 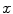 axis, which represents the lowest possible color value in the corresponding channel, and the eigenvector corresponding to the largest eigenvalue. For example, in channel
axis, which represents the lowest possible color value in the corresponding channel, and the eigenvector corresponding to the largest eigenvalue. For example, in channel 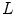 , a tensor with
, a tensor with 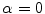 encodes black, whereas a tensor with
encodes black, whereas a tensor with 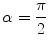 encodes white. In addition, local uniformity and edginess are encoded by means of the normalized
encodes white. In addition, local uniformity and edginess are encoded by means of the normalized 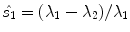 and
and 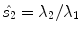 saliencies respectively. Thus, a pixel located at a completely uniform region is represented by means of three stick tensors, one for each color channel. In contrast, a pixel located at an ideal edge is represented by means of three ball tensors, one for every color channel.
saliencies respectively. Thus, a pixel located at a completely uniform region is represented by means of three stick tensors, one for each color channel. In contrast, a pixel located at an ideal edge is represented by means of three ball tensors, one for every color channel.
Fig. 3
Encoding process for channel 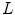 . Color, uniformity and edginess are encoded by means of
. Color, uniformity and edginess are encoded by means of 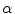 and the normalized saliencies
and the normalized saliencies 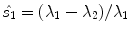 and
and 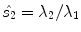 respectively
respectively
 . Color, uniformity and edginess are encoded by means of
. Color, uniformity and edginess are encoded by means of 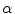 and the normalized saliencies
and the normalized saliencies 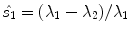 and
and 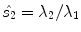 respectively
respectivelyBefore applying the voting process, it is necessary to initialize the tensors associated with every pixel. The colors of the noisy image can be easily encoded by means of the angle 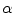 between the
between the 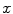 axis and the principal eigenvector, as described above. However, since metrics of uniformity and edginess are usually unavailable at the beginning of the voting process, normalized saliency
axis and the principal eigenvector, as described above. However, since metrics of uniformity and edginess are usually unavailable at the beginning of the voting process, normalized saliency 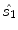 is initialized to one and normalized saliency
is initialized to one and normalized saliency 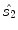 to zero. These initializations allow the method to estimate more appropriate values of the normalized saliencies for the next stages, as described in the next subsection. Thus, the initial color information of a pixel is encoded through three stick tensors oriented along the directions that represent that color in the normalized CIELAB channels:
to zero. These initializations allow the method to estimate more appropriate values of the normalized saliencies for the next stages, as described in the next subsection. Thus, the initial color information of a pixel is encoded through three stick tensors oriented along the directions that represent that color in the normalized CIELAB channels:
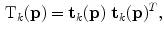
where 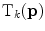 is the tensor of the
is the tensor of the 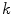 th color channel (
th color channel ( and
and 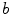 ) at pixel
) at pixel ![$$\mathbf {p},\, \mathbf {{t}}_k(\mathbf {{p}})=\left[ \cos \left( \mathrm {C}_k(\mathbf {{p}})\right) ~~ \sin \left( \mathrm {C}_k(\mathbf {{p}})\right) \right] ^T$$](/wp-content/uploads/2016/03/A308467_1_En_9_Chapter_IEq89.gif) , and
, and 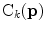 is the normalized value of the
is the normalized value of the 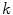 -th color channel at
-th color channel at 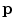 .
.
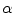 between the
between the 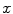 axis and the principal eigenvector, as described above. However, since metrics of uniformity and edginess are usually unavailable at the beginning of the voting process, normalized saliency
axis and the principal eigenvector, as described above. However, since metrics of uniformity and edginess are usually unavailable at the beginning of the voting process, normalized saliency 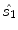 is initialized to one and normalized saliency
is initialized to one and normalized saliency 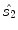 to zero. These initializations allow the method to estimate more appropriate values of the normalized saliencies for the next stages, as described in the next subsection. Thus, the initial color information of a pixel is encoded through three stick tensors oriented along the directions that represent that color in the normalized CIELAB channels:
to zero. These initializations allow the method to estimate more appropriate values of the normalized saliencies for the next stages, as described in the next subsection. Thus, the initial color information of a pixel is encoded through three stick tensors oriented along the directions that represent that color in the normalized CIELAB channels: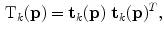
(12)
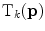 is the tensor of the
is the tensor of the 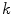 th color channel (
th color channel ( and
and 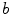 ) at pixel
) at pixel ![$$\mathbf {p},\, \mathbf {{t}}_k(\mathbf {{p}})=\left[ \cos \left( \mathrm {C}_k(\mathbf {{p}})\right) ~~ \sin \left( \mathrm {C}_k(\mathbf {{p}})\right) \right] ^T$$](/wp-content/uploads/2016/03/A308467_1_En_9_Chapter_IEq89.gif) , and
, and 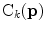 is the normalized value of the
is the normalized value of the 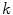 -th color channel at
-th color channel at 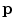 .
.3.2 Voting Process
The voting process requires three measurements for every pair of pixels 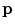 and
and 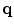 : the perceptual color difference,
: the perceptual color difference, 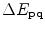 ; the joint uniformity measurement,
; the joint uniformity measurement, 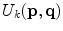 , used to determine if both pixels belong to the same region; and the likelihood of a pixel being impulse noise,
, used to determine if both pixels belong to the same region; and the likelihood of a pixel being impulse noise, 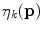 .
. 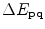 is calculated through CIEDE2000 [13], while
is calculated through CIEDE2000 [13], while
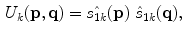
and
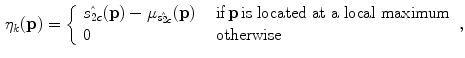
where 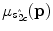 represents the mean of
represents the mean of 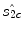 over the neighborhood of
over the neighborhood of 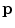 .
.
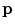 and
and 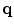 : the perceptual color difference,
: the perceptual color difference, 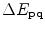 ; the joint uniformity measurement,
; the joint uniformity measurement, 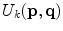 , used to determine if both pixels belong to the same region; and the likelihood of a pixel being impulse noise,
, used to determine if both pixels belong to the same region; and the likelihood of a pixel being impulse noise, 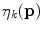 .
.  is calculated through CIEDE2000 [13], while
is calculated through CIEDE2000 [13], while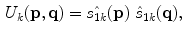
(13)
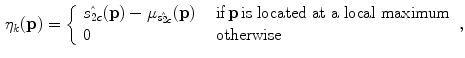
(14)
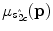 represents the mean of
represents the mean of 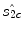 over the neighborhood of
over the neighborhood of 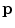 .
.In the second step of the method, the tensors associated with every pixel are propagated to their neighbors through a convolution-like process. This step is independently applied to the tensors of every channel (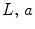 and
and 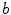 ). The voting process is carried out by means of specially designed tensorial functions referred to as propagation functions, which take into account not only the information encoded in the tensors but also the local relations between neighbors. Two propagation functions are proposed for edge detection: a stick and a ball propagation function. The stick propagation function is used to propagate the most likely noiseless color of a pixel, while the ball propagation function is used to increase edginess where required. The application of the first function leads to stick votes, while the application of the second function produces ball votes. Stick votes are used to eliminate noise and increase the edginess where the color of the voter and the voted pixels are different. Ball votes are used to increase the relevance of the most important edges.
). The voting process is carried out by means of specially designed tensorial functions referred to as propagation functions, which take into account not only the information encoded in the tensors but also the local relations between neighbors. Two propagation functions are proposed for edge detection: a stick and a ball propagation function. The stick propagation function is used to propagate the most likely noiseless color of a pixel, while the ball propagation function is used to increase edginess where required. The application of the first function leads to stick votes, while the application of the second function produces ball votes. Stick votes are used to eliminate noise and increase the edginess where the color of the voter and the voted pixels are different. Ball votes are used to increase the relevance of the most important edges.
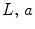 and
and 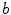 ). The voting process is carried out by means of specially designed tensorial functions referred to as propagation functions, which take into account not only the information encoded in the tensors but also the local relations between neighbors. Two propagation functions are proposed for edge detection: a stick and a ball propagation function. The stick propagation function is used to propagate the most likely noiseless color of a pixel, while the ball propagation function is used to increase edginess where required. The application of the first function leads to stick votes, while the application of the second function produces ball votes. Stick votes are used to eliminate noise and increase the edginess where the color of the voter and the voted pixels are different. Ball votes are used to increase the relevance of the most important edges.
). The voting process is carried out by means of specially designed tensorial functions referred to as propagation functions, which take into account not only the information encoded in the tensors but also the local relations between neighbors. Two propagation functions are proposed for edge detection: a stick and a ball propagation function. The stick propagation function is used to propagate the most likely noiseless color of a pixel, while the ball propagation function is used to increase edginess where required. The application of the first function leads to stick votes, while the application of the second function produces ball votes. Stick votes are used to eliminate noise and increase the edginess where the color of the voter and the voted pixels are different. Ball votes are used to increase the relevance of the most important edges.A stick vote can be seen as a stick-shaped tensor, 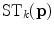 , with a strength modulated by three scalar factors. The proposed stick propagation function,
, with a strength modulated by three scalar factors. The proposed stick propagation function, 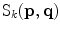 , which allows a pixel
, which allows a pixel 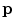 to cast a stick vote to a neighboring pixel
to cast a stick vote to a neighboring pixel 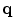 for channel
for channel 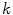 is given by:
is given by:
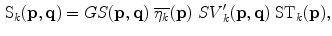
with 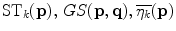 and
and 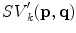 being defined as follows. First, the tensor
being defined as follows. First, the tensor 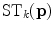 encodes the most likely normalized noiseless color at
encodes the most likely normalized noiseless color at 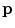 . Thus,
. Thus, 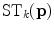 is defined as the tensorized eigenvector corresponding to the largest eigenvalue of the voter pixel, that is:
is defined as the tensorized eigenvector corresponding to the largest eigenvalue of the voter pixel, that is:
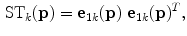
being 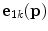 the eigenvector with the largest eigenvalue of the tensor associated with channel
the eigenvector with the largest eigenvalue of the tensor associated with channel 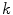 at
at 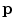




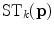 , with a strength modulated by three scalar factors. The proposed stick propagation function,
, with a strength modulated by three scalar factors. The proposed stick propagation function, 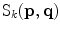 , which allows a pixel
, which allows a pixel 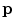 to cast a stick vote to a neighboring pixel
to cast a stick vote to a neighboring pixel 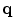 for channel
for channel 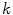 is given by:
is given by: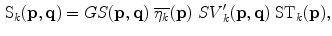
(15)
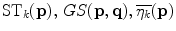 and
and 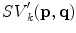 being defined as follows. First, the tensor
being defined as follows. First, the tensor 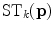 encodes the most likely normalized noiseless color at
encodes the most likely normalized noiseless color at 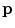 . Thus,
. Thus, 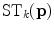 is defined as the tensorized eigenvector corresponding to the largest eigenvalue of the voter pixel, that is:
is defined as the tensorized eigenvector corresponding to the largest eigenvalue of the voter pixel, that is: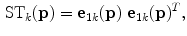
(16)
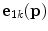 the eigenvector with the largest eigenvalue of the tensor associated with channel
the eigenvector with the largest eigenvalue of the tensor associated with channel 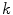 at
at 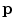
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree




