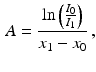(1)
Department of Mathematics and Statistics, Villanova University, Villanova, PA, USA
Electronic supplementary material
The online version of this chapter (doi:10.1007/978-3-319-22665-1_1) contains supplementary material, which is available to authorized users.
1.1 Introduction
A computerized axial tomography (CAT or CT) scan is generated from a set of thousands of X-ray beams, consisting of 160 or more beams at each of 180 directions. To comprehend this large collection of X-rays, we must first understand just one beam.
When a single X-ray beam of known intensity passes through a medium, such as muscle or brain tissue or an ancient Egyptian sarcophagus , some of the energy present in the beam is absorbed by the medium and some passes through. The intensity of the beam as it emerges from the medium can be measured by a detector. The difference between the initial and final intensities tells us about the ability of the medium to absorb energy. For the sort of X-rays one might get at the dentist’s office or for a suspected broken bone, the detector is a piece of film. A fan- or cone-shaped set of X-rays is emitted from a machine and those photons that are not blocked or absorbed by teeth or bone expose the film, thus creating a picture of the medium. The picture essentially lacks depth since anything positioned behind a point where the photons are blocked will not be seen. This shortcoming highlights a significant difficulty in imaging, namely, that the medium through which the X-rays pass is not homogeneous. For instance, muscles are fibrous and denser in some parts than others; brain tissue is composed of grey matter, water, blood, neurons, and more; inside the sarcophagus is a mummified, partly decomposed body, but also remains of objects that were buried along with the deceased.
The idea behind the CT scan is that, by measuring the changes in the intensity of X-ray beams passing through the medium in different directions and, then, by comparing the measurements, we might be able to determine which locations within the medium are more absorbent or less absorbent than others.
To get an idea of how this works, let’s start with a simple model. Suppose we have a one-centimeter-thick slice of material (the medium) in the shape of a square. The square is divided into a 3-by-3 rectangular grid of smaller squares each of which is either black or white. Each white square absorbs “1 unit” of X-ray energy while the black squares do not absorb X-ray energy. (So the white squares act like bone, say, and the black ones act like air.) Suppose now that an X-ray beam passing through the first row of the grid loses 2 energy units. It follows that there must be two white squares, and one black square, in the first row of the grid. If an X-ray beam passing through the first column of the grid loses 1 unit of energy, then the first column would contain only one white square. At this point, there are only four possibilities for the configuration of the first row and column (instead of the initial 25 = 32 possibilities for these five squares), namely, Row 1 = WWB and Column 1 = WBB; Row 1 = WBW and Column 1 = WBB; Row 1 = BWW and Column 1 = BWB; or Row 1 = BWW and Column 1 = BBW. Continuing in this way, suppose that we measure the following losses in X-ray energy for the various rows and columns of the grid: Row 1 → 2 units lost; Row 2 → 2 units; Row 3 → 1 unit; Column 1 → 1 unit; Column 2 → 2 units; and Column 3 → 2 units of energy lost. Figure 1.1 shows one of several possible configurations of black and white squares that are consistent with these measurements.


Fig. 1.1
This grid of white and black squares has a prescribed X-ray energy absorption for each row and column.
What are the other possible configurations? Is there an easy way to determine the total number of white squares, and, consequently, the total number of black squares, in the grid? Is there more than one consistent pattern? If so, what additional information might help to pinpoint a unique shading pattern? For a rich and highly entertaining elaboration on this model for thinking about CT scans, see [16].
In some sense, creating an image from a CT scan consists of carrying out a scheme like this on a rectangular image grid subdivided into thousands of small squares. Instead of just black or white, each square is assigned a greyscale value — a number between 0 and 1, where, by common practice, black is 0 and white is 1 — based on the energy-absorption ability of the material located in that square in the grid. Each X-ray passing through the material is measured, and the change in intensity gives us information about the amount of grey encountered along the path of the beam. What is not known is precisely where along the way the reduction in energy occurred. Once we know the changes in intensity for enough X-rays, we try to create an image whose greyscale values are consistent with the measurements. This approach to image construction is akin to the basic idea implemented by Hounsfield in his early CT scanners and will be discussed in a more refined way in Chapter 9
Example with R 1.1.
There are two ways to produce an image like that in Figure 1.1 using R. The polygon command allows one to have defined borders within the grid. Otherwise, the image command converts a matrix of numbers into a grid of boxes colored according to the matrix entries. The code used here is the following:
##Fig 1.1 has three polygonal regions
x1=c(1,0,0,1,1,1,1,2,2,3,3,3,2,2,1)
y1=c(2,2,3,3,2,1,0,0,1,1,2,3,3,2,2)
x2=c(1,0,0,1,1,1,2,2,1)
y2=c(2,2,0,0,2,3,3,2,2)
x3=c(2,2,3,3,2)
y3=c(0,1,1,0,0)
plot(0:3, 0:3, type = “n”)
polygon(x1, y1, col = “white”,border = “black”)
polygon(x2, y2, col = “black”,border = “black”)
polygon(x3, y3, col = “black”,border = “black”)
lines(c(1,2,2,3),c(1,1,2,2))
1.2 X-ray behavior and Beer’s law
To simplify the analysis, we will make some assumptions that present an idealized view of what an X-ray is and how it behaves. Specifically, in thinking of an X-ray beam as being composed of photons, we will assume that the beam is monochromatic. That is, each photon has the same energy level E and the beam propagates at a constant frequency, with the same number of photons per second passing through every centimeter of the path of the beam. If N(x) denotes the number of photons per second passing through a point x, then the intensity of the beam at the point x is
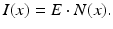 We also assume that an X-ray beam has zero width and that it is not subject to refraction or diffraction. That is, X-ray beams are not bent by the medium nor do they spread out as they propagate.
We also assume that an X-ray beam has zero width and that it is not subject to refraction or diffraction. That is, X-ray beams are not bent by the medium nor do they spread out as they propagate.
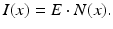
Every substance through which an X-ray passes has the property that each millimeter of the substance absorbs a certain proportion of the photons that pass through it. This proportion, which is specific to the substance, is called the attenuation coefficient of that material. The units of the attenuation coefficient are something like “proportion of photons absorbed per millimeter of the medium.” In general the attenuation coefficient is non-negative and its value depends on the substance involved. Bone has a very high attenuation coefficient, air has a low coefficient, and water is somewhere in between. Different soft tissues have slightly different attenuation coefficients associated with them.
Radiologists actually use a variant of the attenuation coefficient in their work. Developed by Godfrey Hounsfield, the Hounsfield unit associated with a medium is a number that represents a comparison of the attenuation coefficient of the medium with that of water. Specifically, the Hounsfield unit of a medium is
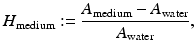
where A denotes the true attenuation coefficient. Table 1.1 gives the Hounsfield units of some typical organic substances.
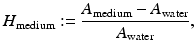
(1.1)
Table 1.1
Approximate Hounsfield units for certain organic substances.
substance | Hounsfield units | substance | Hounsfield units |
|---|---|---|---|
bone | 1000 | kidney | 30 |
liver | 40 to 60 | cerebrospinal fluid | 15 |
white matter | 20 to 30 | water | 0 |
grey matter | 37 to 45 | fat | − 100 to − 50 |
blood | 40 | air | − 1000 |
muscle | 10 – 40 |
Now suppose an X-ray beam passes through some medium located between the position x and the position 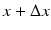 , and suppose that A(x) is the attenuation coefficient of the medium located there. Then the proportion of all photons that will be absorbed in the interval
, and suppose that A(x) is the attenuation coefficient of the medium located there. Then the proportion of all photons that will be absorbed in the interval ![$$[x,\,x + \Delta x]$$](/wp-content/uploads/2016/10/A183987_2_En_1_Chapter_IEq2.gif) is
is 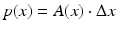 . Thus the number of photons that will be absorbed per second by the medium located in the interval
. Thus the number of photons that will be absorbed per second by the medium located in the interval ![$$[x,\,x + \Delta x]$$](/wp-content/uploads/2016/10/A183987_2_En_1_Chapter_IEq4.gif) is
is 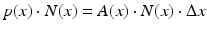 . If we multiply both sides by the energy level E of each photon, we see that the corresponding loss of intensity of the X-ray beam over this interval is
. If we multiply both sides by the energy level E of each photon, we see that the corresponding loss of intensity of the X-ray beam over this interval is
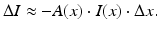 Let
Let 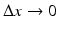 to get the differential equation known as Beer’s law:
to get the differential equation known as Beer’s law:
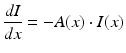
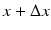 , and suppose that A(x) is the attenuation coefficient of the medium located there. Then the proportion of all photons that will be absorbed in the interval
, and suppose that A(x) is the attenuation coefficient of the medium located there. Then the proportion of all photons that will be absorbed in the interval ![$$[x,\,x + \Delta x]$$](/wp-content/uploads/2016/10/A183987_2_En_1_Chapter_IEq2.gif) is
is 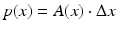 . Thus the number of photons that will be absorbed per second by the medium located in the interval
. Thus the number of photons that will be absorbed per second by the medium located in the interval ![$$[x,\,x + \Delta x]$$](/wp-content/uploads/2016/10/A183987_2_En_1_Chapter_IEq4.gif) is
is 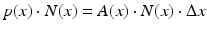 . If we multiply both sides by the energy level E of each photon, we see that the corresponding loss of intensity of the X-ray beam over this interval is
. If we multiply both sides by the energy level E of each photon, we see that the corresponding loss of intensity of the X-ray beam over this interval is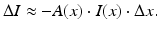
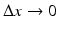 to get the differential equation known as Beer’s law:
to get the differential equation known as Beer’s law: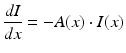
(1.2)
This may also be stated as follows.
Beer’s law. The rate of change of intensity per millimeter of a nonrefractive, monochromatic, zero-width X-ray beam passing through a medium is jointly proportional to the intensity of the beam and to the attenuation coefficient of the medium. This condition is expressed by the differential equation (1.2).
The differential equation (1.2) is separable and can be written as
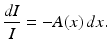 If the beam starts at location x 0 with initial intensity I 0 = I(x 0) and is detected, after passing through the medium, at the location x 1 with final intensity I 1 = I(x 1), then we get
If the beam starts at location x 0 with initial intensity I 0 = I(x 0) and is detected, after passing through the medium, at the location x 1 with final intensity I 1 = I(x 1), then we get
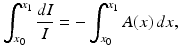 from which it follows that
from which it follows that
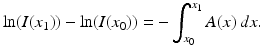 Thus
Thus
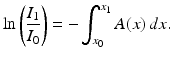 Multiplying both sides by − 1 yields the result
Multiplying both sides by − 1 yields the result
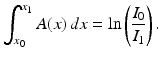
This is a little bit backwards from what we often encounter in textbook problems in differential equations. There, we would typically know the coefficient function and use integration to find the function I. Here, however, we know the initial and final values of I, and it is the coefficient function A, which expresses an essential property of the medium being sampled by the X-ray, that is unknown. Thus, we see that from the measured intensity of the X-ray we are able to determine not the values of A itself, but rather the value of the integral of A along the line of the X-ray.
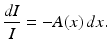
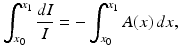
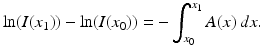
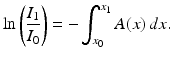
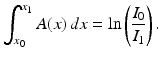
(1.3)
Example 1.2.
For a simple example, suppose the attenuation-coefficient function A is constant throughout a sample. Then, the amount of absorption along any given X-ray beam depends only on the width of the sample along the line of the beam. So, if the beam is travelling along the x-axis and enters the sample at x 0, say, and leaves the sample at x 1, then the amount of absorption is A(x 1 − x 0). It follows from (1.3) that