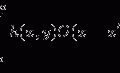Fig. 5.1
Angular-temporal photon distribution of a 20-fs ultrashort pulsed beam propagating through a turbid slab (l s = 40 μm, d/l s = 4). The time t is a local time, so t = 0 corresponds to the arrival time of the unscattered pulse peak. a Illumination with a circular objective; b illumination with an annular objective. Reprinted with permission from [3], 1997, Cambridge University Press
The use of an annular imaging objective to perform an effective angle-gating mechanism [2] is demonstrated in Fig. 5.1b which illustrates the angular-temporal photon distribution under illumination with a thin annular objective (ε = 0.9). An annular lens is simulated in the Monte Carlo model by confining the x–y coordinate of point A (see Fig. 3.1) to a circular ring instead of a circular area. It is noted that under this configuration there is a distinguishable unscattered photon peak in both angular and temporal domains. According to geometric optics, a thin annular aperture confines illumination photons to a small region. Therefore, the exit angles of the unscattered photons can remain in these small regions, while the scattered photons exit in a much broader angle range. Figure 5.1b also shows that once a photon is scattered, the possibility for such a photon returning to the original direction is very small. Therefore, the amount of the scattered photons in the angle region defined by the annular objective is small. This phenomenon is produced under illumination with a thin annular lens provides a physical basis to distinguish the scattered and unscattered photons in the angle domain in a microscopic imaging system.
5.1.2 Angle-Gating in a Microscope
Without losing generality, let us consider a transmission optical microscope. Figure 5.2 shows the concept of angle-gating in a transmission optical microscope, where a darker region includes more ballistic photons . When one employs a pair of circular objectives (O1 and O2) in a transmission optical imaging system (Fig. 5.2a), there is no physical way to separate scattered photons in the angle domain of the second (collection) objective O2. In order to separate these two types of photons, an annular objective (an annular objective can be achieved by placing an annular filter F in the front focal plane of an objective in a 4f system [2]) rather than a circular objective is needed for illumination. The size of an annular objective , ε, is defined as the ratio of the central obstruction radius to the objective aperture radius. ε in and ε out are used to define annular objectives in the illumination and collection paths, respectively. It should be noted that the range of the illumination angles for an annular objective is reduced but the numerical aperture of the objective does not change since the maximum aperture of the objective does not change. As expected, with the introduction of an illumination annular objective, it is possible to separate the scattered and unscattered photons from each other since the scattered photons statistically propagate along different angles from the unscattered photons (Fig. 5.2b).
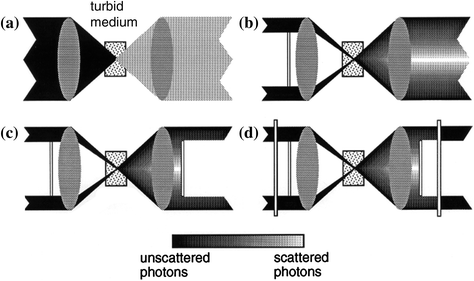

Fig. 5.2
Principle of angle-gating in a transmission microscopic imaging system when a a pair of circular objectives, b an illumination annular objective and a collection circular objective, c a matching pair of annular objectives and d a matching pair of annular objectives employing polarization-gating are employed
To make use of this unscattered photon peak for high-quality microscopic imaging, one can employ another thin annular filter F2 to collect the signal originating from the object embedded in turbid media, as depicted in Fig. 5.2c. Although a pair of annular objectives can eliminate scattered photons which do not travel along the same direction of the illumination beam, there are still photons which are multiply scattered and finally travel along the same direction as the illumination beam. These scattered photons are superimposed on top of the unscattered photons and can lead to a reduction of image quality (resolution and contrast) even when annular objectives are employed, since multiply scattered photons carry less information of an object embedded in a turbid medium. These scattered photons do not possess the same polarization state as the incident beam because of the scattering process. Therefore to suppress them, one can insert a polarizer LP1 in front of or after the illumination annular filter (Fig. 5.2d), so that unscattered photons coming from the sample have the same polarization state as the illumination while the scattered photons traveling along the illumination direction are depolarized. The amount of diffusing photons can be appreciably reduced by using another polarizer LP2, (Fig. 5.2d) which has the same polarization direction as the incident beam and is placed in the back focal plane of the collection objective. As a result of incorporating a polarization detection mechanism, image quality (resolution and contrast) can be further improved.
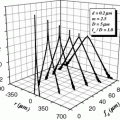
To confirm the angle-gating mechanism, we can use the Monte Carlo program [3–5] to calculate the intensity distribution over the collection objective aperture O2 for a continuos wave beam for sample3 and sample5 (see Table 5.1) which was used in the experiments. Illustrated in Fig. 5.3 is the intensity distribution, normalized by the incident intensity, along the radial direction of the collection objective, r, when a circular (ε = 0) or an annular objective (ε = 0.9) is employed for illumination. It can be seen from Fig. 5.3 that an unscattered photon peak appears near the edge of the collection objective aperture only when an annular objective is used for illumination. This result confirms that the thin illumination annular objective confines the unscattered photons to a small angular region on the collection objective plane. The unscattered photon peak in the case of sample5 (Fig. 5.3b) is not as strong as that for sample3 (Fig. 5.3a) due to the significant difference in the average number of scattering events (see Table 5.1).
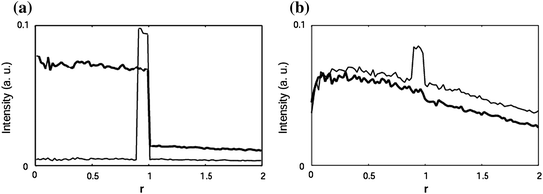
Table 5.1
Parameters for the samples used in the transmission optical microscope
Sample number | Scattering medium | Cell thickness, d (μm) | SMFP length, l s (μm) | Anisotropy value, g | Optical thickness, n (d/l s) |
|---|---|---|---|---|---|
1 | Distilled water | 100 | – | – | – |
2 | 0.107 μm polysty. microsph. in water | 120 | 416.4a | 0.076a | 0.3 |
3 | 0.202 μm polysty. microsph. in water | 120 | 70.2a | 0.31a | 1.7 |
4 | 0.48 μm polysty. microsph. in water | 100 | 19.2a | 0.81a | 5.2 |
5 | 0.48 μm polysty. microsph. in water | 120 | 19.2a | 0.81a | 6.3 |
6 | Semi-skimmed milk | 100 | 30b | <0.4c | 3.3 |
7 | Semi-skimmed milk | 300 | 30b | <0.4c | 10 |

Fig. 5.3
Simulated photon distribution along the radial direction of the collection objective for illumination with a circular objective (ε = 0, bold) or an annular objective (ε = 0.9). a Sample3 (a turbid medium consisting of 0.202 μm microspheres, see Table 5.1); b sample5 (a turbid medium consisting of 0.48 μm microspheres, see Table 5.1). Here ρ is the radial coordinate of the collection objective, normalized by the maximum radius of the objective. Reprinted with permission from [6], 1998, Wiley
5.2 Angle-Gating in Transmission Optical Microscopy
5.2.1 Transmission Optical Microscope and Turbid Samples
The transmission optical microscope shown in Fig. 5.4a is a scanning optical microscope using two polarized annular objectives [5]. A 7 mW Melles Griot (model No. 05-LHP-153) He–Ne laser (λ = 632.8 nm) is used as the light source. The beam from the laser source is expanded and collimated by an objective O1 (numerical aperture, NA = 0.25) and a lens L1 (focal length, f = 200 mm, diameter, D = 25 mm). The illumination objective O2 (Zeiss FLUAR 20×/0.75 ∞/0.17) and the collection objective O3 (Zeiss PLAN-NEOFLUAR 40×/0.75 ∞/0.17) formed a symmetric system around a turbid sample since they have an identical numerical aperture . Scattered and unscattered photons coming from the collection objective are focused via lens L2 (f = 200 mm, D = 25 mm) onto a large area detector (1 cm2) DT which records a time-averaged signal.
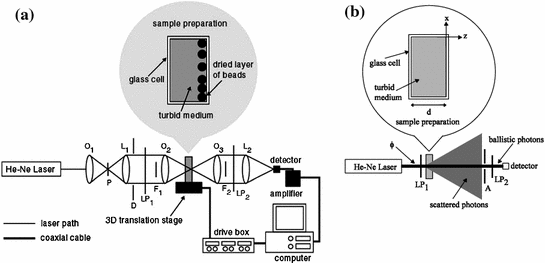

Fig. 5.4
Experimental systems. a Transmission scanning optical microscope with angle-gating and polarization-gating mechanisms. A aperture; DT detector; F central obstruction; L lens; LP polariser; ND neutral density filter; O objective; P pinhole. b Optical system to determine the scattering mean free path length, l s, for semi-skimmed milk. ϕ incident and collection beam diameters; A aperture; LP polarisers. Reprinted with permission from [5], 1998, Optical Society of America
Annular objectives can be achieved by placing coaxially opaque circular disc obstructions F1 and F2 in the illumination and detection beam paths, respectively. Extreme care should be taken when the focal position of the imaging and collection objectives are overlapped and when the position of the central obstructions in the aperture of the illumination and collection objectives are aligned. The performance of the angle-gating mechanism depends on the successful alignment of these two parameters.
The polarization-gating mechanism can be implemented by placing a polarizer LP1 which produced a linearly polarized illumination beam, and a polarizer LP2 which acts as an analyzer in front of the detector. The degree of polarization, γ, defined in (3.1), of the light passing through a turbid sample can be measured from the signals detected with the analyzer LP2 parallel (I p) and perpendicular (I s) to the direction of LP1, respectively. The polarization intensity ratio, the ratio of the parallel polarization intensity to the perpendicular polarization intensity, I p/I s, (where I p/I s ≥ 1) is also used in the experiments to help demonstrate the contribution made by unscattered and scattered photons . Therefore, a large polarization intensity ratio, I p/I s, is desirable since this represents the situation when more unscattered photons are collected than scattered photons.
The details of seven turbid samples are summarized in Table 5.1 [5, 6]. Each sample is placed in an individual glass cell with lateral dimensions of 2 cm × 1 cm. The geometric thickness of the glass cell, d, is varied for the different samples. The optical thickness, n, (i.e., the average number of scattering events experienced by a given photon) is given by, d/l s for a transmission system, where l s is the scattering mean free path (SMFP) length, as defined in (2.11). Sample1 consists of distilled water and is used to determine the behavior of the transmission imaging system without scatterers. Sample2, sample3, sample4, and sample5 consist of polystyrene microspheres suspended in water and the scattering parameters of microspheres in these samples are given in Table 2.1. Sample6 and sample7 consist of standard semi-skimmed milk (fat content 3.6 %). Semi-skimmed milk is chosen since it does not include large scatterers (>1 μm), and has been used by Morgan et al. [8] and Wabnitz and Rinneberg [9] in transillumination imaging to simulate tissues which do not include large scatterers (>1 μm). These samples are chosen so that the performance of the angle-gating mechanism can be experimentally investigated in the regimes when scattering is weak and strong.
The diameter of the scattering particles in the milk suspension is assumed to be in the range of 0.1–1.0 μm, and the anisotropy value was assumed from the reference by Jensen [7]. The scattering mean free path length, l s, for the semi-skimmed milk can be experimentally determined with the experimental arrangement shown in Fig. 5.4b in conjunction with Beers’ law shown in (3.1). Rearranging (3.1) yields
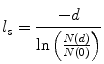
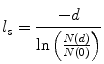
(5.1)
Therefore as long as the incident power, which is proportional to N(0), and the turbid medium thickness, d, are known, the scattering mean free path length, l s, can determined by measuring the transmitted unscattered light intensity, which is proportional to N(d), passing through a given turbid medium. The measurement of the transmitted unscattered light intensity is done in the far field region (approximately 1 m away from the turbid sample) to minimize the detection of scattered photons. An aperture in conjunction with a polarization-gating mechanism is employed in front of the detector to assist in minimizing the contribution made by scattered photons, since scattered photons are depolarized and statistically travel along a different direction from unscattered photons.
For evaluating the image quality when polarized annular objectives are used, a cluster layer of 22 μm (in diameter) polystyrene microspheres (standard deviation 2.593 μm, PolyScience Inc.) can be dried onto the inside back surface of the glass cell before it is filled with a turbid medium. The turbid media are placed between the illumination objective and the object, as shown in Fig. 5.4a. Prepared samples are mounted on a three-dimensional piezoelectric translation stage and then placed in the overlapping focal region of the two objectives O2 and O3. The translation stages are controlled through a piezoelectric controller. The piezoelectric stages provide 200 μm of traversal with 50 and 100 nm resolution in the x–y and z directions, respectively. The overlapping focus of the two objectives O2 and O3 is equally spaced in the center of a turbid sample for the measurements of the degree of polarization , γ. The degree of polarization, γ, for sample1 is measured to be 99.9 % for circular imaging objectives (ε = 0), which shows that depolarization caused by the objectives and other components in this experimental arrangement can be ignored.
5.2.2 Effect of Annular Illumination and Collection Objectives
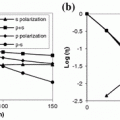
Let us first consider the effect of an annular objective on imaging performance. We take sample4 and sample7 since these two samples can demonstrate the effect of an annular illumination objective when optical scattering is weak and strong. The degree of polarization, γ, with circular illumination and collection (ε in = ε out = 0) objectives is measured to be 0.574 and 0.118 for sample4 and sample7, respectively. This measurement demonstrates the depolarization of the incident beam due to the scatterers in the turbid media.
Measurements of the degree of polarization, γ, for different central obstruction sizes, ε in, placed in the illumination beam path (F1) are plotted in Fig. 5.5. Figure 5.5a shows the effect of the central obstruction size of the illumination objective, ε in, on the degree of polarization, γ, when a circular collection objective (ε out = 0), are employed for sample4 and sample7. Figure 5.5b illustrates the polarization intensity ratio, I p/I s, for the collected signals under the same conditions. It is seen that as the illumination central obstruction size, ε in, increases from 0 to 0.9, the degree of polarization, γ, decreases from 0.574 (or I p/I s = 3.7) to 0.532 (or I p/I s = 3.3) and from 0.118 (or I p/I s = 1.3) to 0.051 (or I p/I s = 1.1) for sample4 and sample7, respectively.
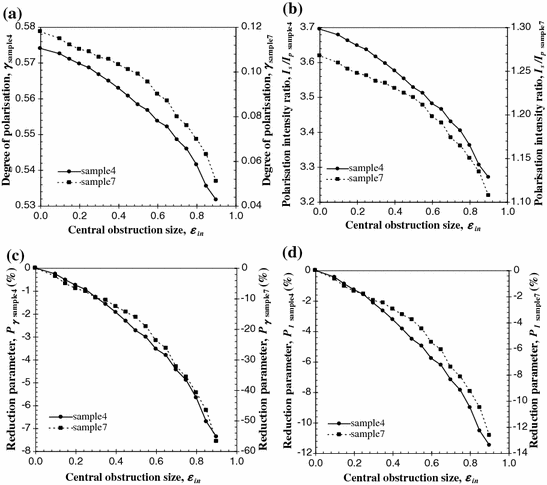

Fig. 5.5
Dependence of the degree of polarization, γ (a), the polarization intensity ratio, I p/I s (b), and the percentage reduction parameters, P γ (c) and P I (d) on the radius of the central obstruction of the illumination objective, ε in. The numerical aperture for objectives O2 and O3 is 0.6
To further help demonstrate the performance of the illumination central obstruction size, ε in, on the suppression of scattered photons the following 2 % improvement/reduction parameters are defined
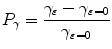
and
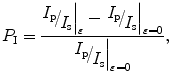
where P γ demonstrates the change in the degree of polarization, γ, and P I demonstrates the change in the polarization intensity ratio, I p/I s.
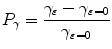
(5.2)
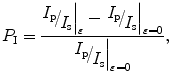
(5.3)
The parameters P γ and P I as a function of the illumination central obstruction size, ε in, for sample4 and sample7 are shown in Figs. 5.5c, d, respectively. It is seen that as the illumination central obstruction size, ε in, increases from 0 to 0.9, P γ and P I decrease by approximately 7 and 11 %, respectively, for sample4, while for sample7 the decrease in P γ and P I is approximately 57 and 13 %, respectively. This behavior is because the annular input confines the illumination photons into a high-angle region. Incident photons traveling at higher angles through the turbid samples experience on average more scattering events, leading to a stronger depolarization effect which is indicated by the lower polarization intensity ratio, I p/I s, when the illumination central obstruction size, ε in, approaches unity (Fig. 5.5b). Since the collection objective collects all the available unscattered and scattered photons within its aperture, scattered photons cannot be further selectively suppressed. Thus the degree of polarization, γ, and the polarization intensity ratio, I p/I s, inevitably decrease.
Now let us turn to the performance of the central obstruction sizes, ε out, placed in the collection beam path (F2), on the degree of polarization, γ, for fixed values of the central obstruction size, ε in, placed in the illumination beam path (F1). Only sample4 is used, since a single turbid sample can demonstrate the effect of the annular collection objective on suppressing scattered photons.
Figure 5.6a shows the dependence of the degree of polarization , γ, on the collection central obstruction size, ε out, (used to suppress the scattered photons) when the central obstruction size, ε in, of the illumination objective is given, while Fig. 5.6b illustrates the polarization intensity ratio, I p/I s, for the collected signal. The parameters P γ and P I are plotted in Fig. 5.6c, d for the four cases, respectively.
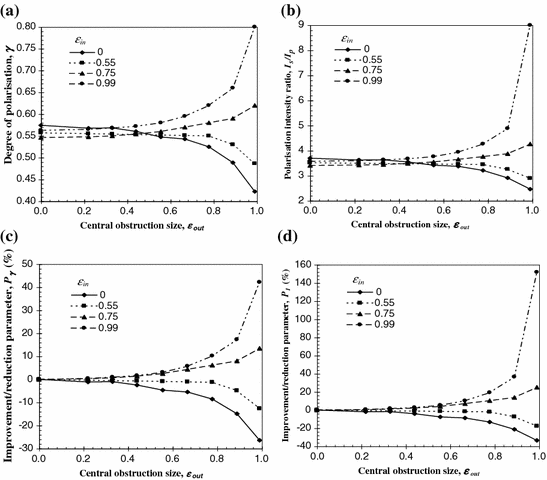

Fig. 5.6
Dependence of the degree of polarization, γ (a), the polarization intensity ratio, I p/I s (b), and the percentage improvement/reduction parameters, P γ (c) and P I (d) on the radius of the central obstruction of the collection objective, ε out, when the central obstruction, ε in, of the illumination objective is given. The numerical aperture for objective O2 and O3 is 0.6
When an annular illumination objective of ε in < 0.75 is employed there is not enough discrimination of the scattered photons even for a collection central obstruction size, ε out, approaching unity. This feature can be further seen from the decreasing values of P γ and P I (i.e., higher contribution of scattered photons) in Fig. 5.6c, d, respectively. It can be clearly seen from Fig. 5.6 that a significant improvement in the degree of polarization, γ, is made only when both central obstruction sizes, ε in and ε out are greater than 0.75. For a collection central obstruction size, ε out, equal to 0.99 the improvement in the degree of polarization, γ, is 0.074 (or P γ ≈ 14 %) and 0.237 (or P γ ≈ 42 %) when an annular objective with central obstruction size, ε in, equal to 0.75 and 0.99, respectively, is used. The improvement in the polarization intensity ratio, I p/I s, for the same conditions is 0.85 (or P I ≈ 25 %) and 5.43 (or P I ≈ 152 %), respectively. This result suggests that a pair of annular objectives with large central obstructions (i.e., ε → 1) should be used to efficiently suppress diffusing photons.
Finally, we examine the performance of two equal central obstruction sizes (ε in = ε out = ε) placed in the illumination beam path (F1) and collection beam path (F2). In this case sample2, sample3, sample4, and sample7 are used. These four samples are chosen to demonstrate the effect of the angle-gating mechanism on the suppression of scattered photons for turbid media with different scattering characteristics. The dependence of the degree of polarization, γ, on the central obstruction size, ε, for a matching pair of annular objectives and the polarization intensity ratio, I p/I s, for the collected signal are shown in Fig. 5.7a, b, respectively. The parameters P γ and P I are plotted in Fig. 5.7c, d for the four samples, respectively.
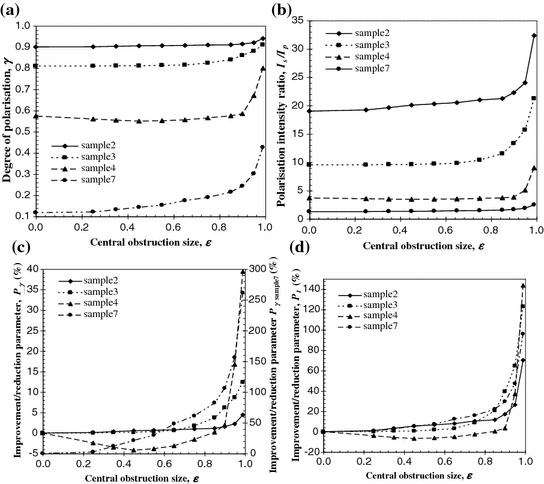

Fig. 5.7
Dependence of the degree of polarization, γ (a), the polarization intensity ratio, I p/I s (b), and the percentage improvement/reduction parameters, P γ (c) and P I (d) on the radius of the central obstruction of a matching pair of annular objectives, ε. The numerical aperture for objectives O2 and O3 is 0.6
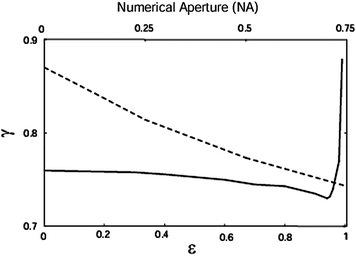
The measured degree of polarization, γ, for the four samples was 0.9 (or I p/I s = 19), 0.81 (or I p/I s = 9.5), 0.574 (or I p/I s = 3.7) and 0.118 (or I p/I s = 1.3), respectively, when circular objectives (ε = 0) is used. The lower degree of polarization, γ, for sample4 and sample7 results from the fact that the scattering effect is much stronger than that for samples2 and sample3. It is clearly seen from Fig. 5.7a that the degree of polarization, γ, increases appreciably when the central obstruction size, ε, changes from zero to unity. The difference of the degree of polarization, γ, between the matching pair of circular objectives (ε = 0) and the matching pair of annular objectives (ε ≈ 0.99) was 0.04 (or P γ ≈ 4 %), 0.1 (or P γ ≈ 12 %), 0.226 (or P γ ≈ 39 %) and 0.308 (or P γ ≈ 261 %) for sample2, sample3, sample4 and sample7, respectively. The corresponding improvement in the polarization intensity ratio, I p/I s is 13.3 (or P I ≈ 70 %), 11.7 (or P I ≈ 123 %), 5.3 (or P I ≈ 144 %) and 1.2 (or P I ≈ 96 %) for sample2, sample3, sample4, and sample7, respectively. This result clearly shows that if two thin polarizing annular objectives are used diffusing photons can be efficiently suppressed and that the effect of the polarizing annular objectives on the suppression becomes more significant when the optical thickness , n, becomes larger and depolarization is stronger. The degree of polarization, γ, increases quickly when the central obstruction size, ε, is greater than 0.9, which implies that the improvement in image quality becomes significant in this region. Although an annular objective with the central obstruction size, ε, close to unity allows higher suppression of scattered photons, such a large central obstruction size, ε, reduces the amount of detectable photons appreciably. Therefore, a trade-off value of the central obstruction size, ε, exists between the signal-to-noise ratio of an image and the ability to suppress scattered photons (i.e., resolution achievable).
In Fig. 5.7a sample4 shows that the degree of polarization, γ, decreases first and then increases when the central obstruction size, ε, changes from 0 to 0.9. This phenomenon is caused by the competition between two processes occurring when the central obstruction size, ε, increases. The first process is that increasing the central obstruction size, ε in, of the imaging objective results in more scattering events due to the longer propagation path of scattered photons and leads to a reduction of the degree of polarization, γ, as shown in Fig. 5.5. On the other hand, when a pair of matching annular objectives with a central obstruction size, ε > 0.75 are used, scattered photons can be suppressed and therefore the degree of polarization, γ, increased. The second process becomes dominant when the central obstruction size, ε, approaches unity. As a result, a decreased degree of polarization , γ, occurs for sample4 when the central obstruction size, ε, is not large enough. Once the central obstruction size, ε, is large enough, the degree of polarization, γ, increases appreciably, due to the dominance of the second process. For sample2, sample3, and sample7, it seems that the second process is always dominant. The behavior regarding the effect of the size of the central obstruction, ε, on the degree of polarization, γ, for sample4 is qualitatively confirmed by the theoretical result in Fig. 5.8, which is based on the Monte Carlo method described in Chap. 3 [3].