2.2.1

Background

The MR resonance frequency, the Larmor frequency, is proportional to the magnetic flux density. MRI and MRS rely on the assumption that, in the absence of pulsed field gradients, the Larmor frequency of all (magnetically equivalent) spins is virtually identical, independent of their position within the object, slice, or voxel. Only then is the assignment of the Larmor frequencies to specific chemical shifts or, in the presence of pulsed field gradients, to spatial coordinates in the gradient direction unambiguous, accurate, and correct. Any deviation from a perfectly homogeneous field of the flux density, such as an offset, a field gradient, or a more complex field variation, disturbs these assignments and can result in misassigned chemical shifts and a wrong localization.

Spatial encoding with pulsed field gradients is based on the linear increase of the field along the gradient direction. Field inhomogeneities superimpose the field of the pulsed gradient, and the resulting field can be shifted, distorted, rotated, and bended. This can cause a misregistration of slice-selective RF excitations and of the acquired signal, yielding incorrect slice positions, orientations, and thicknesses and geometric distortions of the image ( Figure 2.2.1 ). Slice shifts can also reduce the effective slice thickness, and, thus, the signal intensity in RF refocused acquisitions like spin-echo imaging is diminished if the induced shifts vary between the different RF excitations. These effects are not very pronounced for standard spin-echo and gradient-echo imaging; however, they could hamper quantitative measurements in regions with considerable field inhomogeneities (e.g., close to major air cavities and the body surface or implants and devices). Furthermore, quantitative diffusion-weighting experiments that are also based on pulsed field gradients can also be affected by field inhomogeneities (see Section 2.2.9 ).

Examples for artifacts induced by field inhomogeneities in standard gradient-echo and spin echo imaging of a phantom. While the upper row shows images obtained with an optimum shim setup, the lower row was acquired with linear field gradients in (A) slice selection, (B) frequency-encoding (left-right), and (C) phase-encoding directions that were realized by an offset on the static shim current of the gradient coil. They yield (A) a shift of the slices, (B, C) a slice tilt around (B) a vertical and (C) a horizontal axis, (B) a compression in the left-right direction, and (C) a shearing in the image plane.

Many fast-imaging techniques, like steady-state free precession (SSFP) or spiral imaging, are very sensitive to field inhomogeneities and already exhibit severe image artifacts like banding artifacts and image blurring for moderate field variations. In particular, echo-planar imaging, which is often used for diffusion-weighted and functional neuroimaging, suffers from pronounced geometric distortions in the presence of typical field inhomogeneities, most notably in the phase-encoding direction ( Figure 2.2.2 ).

(A) Reference image and (B–E) examples of artifacts induced by field inhomogeneities in spin echo echo-planar imaging of a phantom. The inhomogeneities were linear field gradients that were realized by an offset on the static shim current of the gradient coil in (C) slice-selection, (D) frequency-encoding (left-right), and (E) phase-encoding directions and cause (C) a slight shift of the image in the phase-encoding direction (up-down), (D) a shearing in the image plane, and (E) a compression in the phase-encoding direction. If the shim current offsets and, thus, the linear field inhomogeneities are inverted, the image shift and the shearing occur in opposite directions, while the compression converts to a stretching. It should be emphasized that the field gradients used here were by a factor of 25 lower than those used in Figure 2.2.1 . Also note that (B) represents an image that is acquired without additional field inhomogeneities (i.e., an optimized standard shim setup) and also exhibits pronounced geometric distortions.

Because field inhomogeneities broaden the frequency distribution of the spins, they can also cause significant intravoxel dephasing. While this effect vanishes in RF refocused (e.g., spin-echo) imaging, it can reduce the signal amplitude considerably in T ₂ ^∗ -weighted acquisitions (see Section 2.2.8 ), as used for functional neuroimaging based on the blood oxygenation level–dependent (BOLD) contrast ( Figure 2.2.3 ). The dephasing increases with the voxel size ( Figure 2.2.3 ) and is usually most pronounced in the slice direction, mainly due to the larger voxel dimension often used in this direction.

Examples of the signal loss induced by through-slice dephasing in T ₂ ^∗ -weighted imaging of a phantom with a slice thickness of 5 mm (upper) and 2 mm (lower). A linear field gradient was applied in the slice direction that increases from left to right. The signal loss is much higher for the thicker sections.

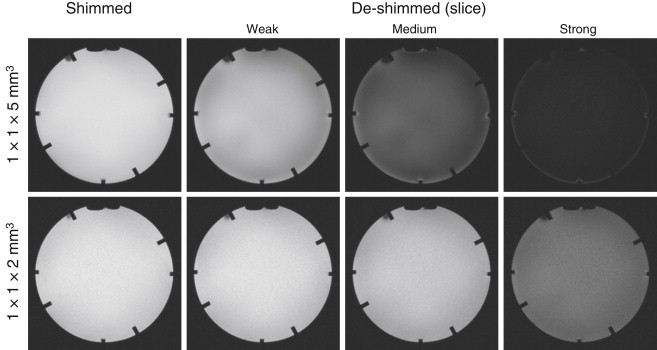
In spectroscopy, field inhomogeneities broaden the line width, which reduces the peak amplitudes, distorts the line shape, and can shift the frequency of peaks ( Figure 2.2.4 ). These effects hinder the reliable detection and unambiguous identification of metabolite-specific peaks, couplings, and patterns ( Figure 2.2.4 ), and they hamper the quantification of metabolite concentrations (see Section 2.2.10 ). Furthermore, chemical-shift selective excitation or acquisition schemes (e.g., water suppression, fat saturation, or spectral editing) can be disturbed considerably, which may also affect imaging experiments.

Examples of the artifacts in MRS in the presence of field inhomogeneities (a linear field gradient in one direction) in a phantom. Compared to (A) a spectrum acquired with an optimized shim setup, (B) the spectrum with field inhomogeneities exhibits a shift of the peaks, a broadening of the line width, distortions of the line shape, and reduced peak amplitude. These effects severely hamper the reliable detection and quantification of metabolites.

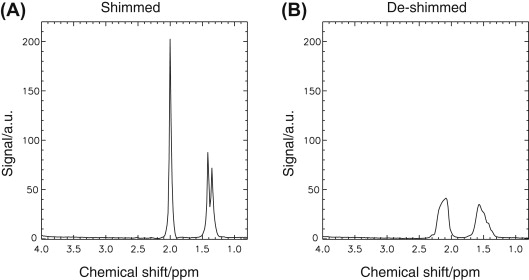
Thus, a sufficiently homogeneous field of the magnetic flux density is crucial for MRI and MRS, and the efforts undertaken to shim the field (i.e., to optimize its homogeneity) are an important part of the adjustment procedure prior to the acquisition (see Section 2.2.7 ) that can improve the image and spectrum quality significantly (see Figures 2.2.1–2.2.4 ).

The static magnetic flux density effectively reflects the combined effect of (1) the magnetic field generated by electric currents (e.g., in the magnet), and (2) the magnetization generated in matter that is exposed to this field (e.g., objects in the magnet bore). The magnetization increases with the field strength and is proportional to the magnetic susceptibility that differs significantly between air, for example around the body and in air-filled cavities like the lung, bones, and biological tissues ( Table 2.2.1 ). Thus, the actual field distribution is not solely defined by the design of the magnet and the adjustment of the magnetic field (e.g., by using the shim coils) but also significantly influenced by the distribution of the magnetic susceptibilities within the bore, i.e., the objects and body in it.

Nowadays, the field homogeneity that can be achieved within the empty bore of the magnet over a typical measurement volume is very high, even for whole-body MR systems. For instance, the relative peak-to-peak variation (i.e., the relative difference between the maximum and the minimum fields) within a sphere with a diameter of 20 cm is typically about or below 0.03 parts per million (ppm) in state-of-the-art 3 T systems, which corresponds to field deviations of less than ±0.05 μT.

Because the differences between the magnetic susceptibilities of air or bones and tissue (see Table 2.2.1 ) are an order of magnitude larger (a few tenths ppm), the body is usually a significant source of field inhomogeneities in vivo. Thus, the field in vivo strongly depends on the geometry and orientation of the body part investigated and the distribution of the magnetic susceptibilities within it, which differs considerably between the different body parts and, to some extent, also between individuals, and can vary during the experiment (e.g., due to respiration). The related field deviations can therefore not be considered in the general setup (e.g., in the design of the magnet) but need to be addressed specifically for each examination and individual with a shim adjustment that, in the presence of motion, ideally is updated during the experiment.

2.2.2

Field Inhomogeneities in the Human Spinal Cord

Field inhomogeneities often hamper MR acquisitions of the human spinal cord, in particular T ₂ ^∗ – and diffusion-weighted imaging and MRS. A minor reason for this is the length of the spinal cord, which could require imaging fields of view as large as 400 mm or beyond in the head–feet direction. The homogeneity of the magnetic field in the empty bore for such a large field of view is typically about 4 ppm on standard 3 T MR systems, which already can cause problems in acquisitions sensitive to field inhomogeneities (see Figure 2.2.2 ). However, more important is the vicinity of the spinal cord to bones, in particular the vertebrae, and air-filled cavities, notably the lung. The magnetic susceptibilities of bone and, in particular, air differ considerably from those of tissue (see Table 2.2.1 ) and the vertebral disks, yielding significant field variations in the human spinal cord.

In all spinal cord sections, the alternation of vertebrae and vertebral disks along the spinal cord is a relevant problem. It effectively causes a periodic modulation of the field in the head–feet direction ( Figure 2.2.5 ). Such a modulation within about one or a few centimeters is hard to correct for with standard shim coils (see Section 2.2.3 ). For about one cycle, i.e., for a few axial slices or within tiny fields of view in the head–feet direction, the shim results achievable may be quite reasonable (see Section 2.2.7 ). But within a larger dimension, i.e., for typical slice stacks used in functional neuroimaging or for MRS voxels, significant inhomogeneities will remain. For axial acquisitions, the slice positions could be chosen to match either the sections within relatively homogeneous fields (i.e., midvertebrae positions) or positions that have very similar field inhomogeneities ( Figure 2.2.5 ), which is easier to correct for with the standard shim methods. However, for many applications, this is not an option.

Anatomical reference images and field maps of the cervical, thoracic, and lumbar parts of the spinal cord. The field maps were acquired with a two-echo FLASH sequence and represent the phase difference of the echoes (see Section 2.2.5 ) without phase unwrapping. The periodic modulation caused by the different susceptibilities of vertebrae and vertebral disks and tissue are visible throughout the cord. Note that the field maps are not corrected for the phase wrap-around (see Section 2.2.5 ), i.e., black and white in neighboring pixels are likely to reflect very similar fields.

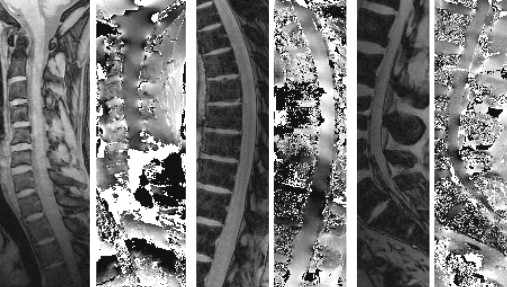
In the lower cervical and upper thoracic section of the spinal cord, significant field variations are caused by the lung ( Figure 2.2.5 ). These inhomogeneities occur on a larger scale and, thus, are easier to address with the standard shim coils (see Section 2.2.3 ), but they are also more variable and much larger in amplitude. Some reduction of these inhomogeneities can be achieved with standard shim methods, but there is still much room for improvements ( Figure 2.2.5 ), inter alia, because the inhomogeneities within the spinal cord depend on the current air volume in the lung (i.e., the respiration state), and motion of the spinal cord may be relevant (e.g., due to respiration).

Thus, the standard shim methods available on common whole-body MR systems provide only a limited correction of the field inhomogeneities in the spinal cord. For the most affected applications, like BOLD-based functional neuroimaging and MRS, this correction is often not sufficient to obtain reasonable image or spectra quality. But more elaborated techniques, such as a dynamic shim update (see Section 2.2.4 ) or z-shimming (see Section 2.2.8 ), could yield a significant improvement.

2.2.3

Shim Hardware

Hardware used for shimming can be divided into two categories. Shim coils driven by an electric current generate an additional magnetic field (“active shim”; see Section 2.2.3.1 ) that superimposes the existing magnetic field (e.g., generated by the magnet). Ferromagnetic, paramagnetic, or diamagnetic materials that are placed in the bore of the magnet (“passive shims”; see Section 2.2.3.2 ) distort the field of the magnetic flux density. Both approaches aim to provide a more homogeneous field in a volume of interest (e.g., around the magnet isocenter or a target volume within the body). However, they differ regarding their flexibility and ability to correct field inhomogeneities. Standard shim coils are somehow limited regarding the field variations that can be compensated, but they can be adjusted flexibly, with an optimized setup being chosen on an acquisition-by-acquisition or even on a slice-by-slice basis (see Section 2.2.4 ). Current passive shim devices are less flexible because their adjustment can be quite time consuming (see Section 2.2.4 ), but they are able to correct more complex field variations.

2.2.3.1

Shim Coils (Active Shim)

Different solutions for shim coils that generate additional magnetic fields have been considered. Commonly available is a set of a few shim coils around the bore, with each of them generating a specific field “pattern”. Adjusting the currents of these shim coils appropriately, a reasonable compensation of typical field inhomogeneities can be attained. However, the homogeneity achievable in specific target volumes may be insufficient for some applications. This is why dedicated shim coils have been proposed that are designed to compensate the specific inhomogeneities that typically remain within the target volume. These coils are much smaller and are positioned close to the target (“local shim coils”). Recently, a promising, more general approach has been presented that involves a fixed array of local coils within the bore around the object. It is able to generate complex field variations, like dedicated local coils, but is more flexible, like the standard shim coils, as it is not constrained to a specific target region.

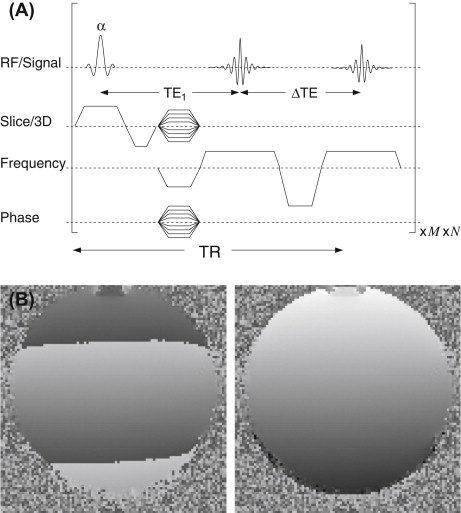
To describe an arbitrary field distribution mathematically, it can be decomposed into a set of basic functions. For the magnetic flux density, a suitable set is based on the so-called spherical harmonics. The individual terms of the decomposition describe unique spatial variations of the field that differ by (1) the power (order) in which the radial coordinate (i.e., the distance from the isocenter) appears in the expressions, and (2) the angular variation. The zeroth-order term corresponds to a homogeneous field, the three first-order terms are linear field variations in three orthogonal directions, and the five second-order terms represent components with a quadratic field variation and more complex angular dependencies (see Figure 2.2.6 ). Accordingly, any linear or higher-order term appearing in the decomposition describes a deviation from the desired homogeneous field and should be compensated. The linear terms can be corrected easily by the gradient coils using an appropriate constant current offset. But second- and higher-order terms require dedicated shim coils that are designed to provide the desired field distribution ( Figure 2.2.6 ).

Field distributions of the coils generating (A) the three linear terms (realized by the gradient coils) and (B) the five second-order terms generated by dedicated room-temperature shim coils acquired in a homogeneous, spherical water phantom in three orthogonal planes. Note that the bottleneck of the phantom causes some minor distortions of the field distribution. The field maps represent the phase difference observed in a two-echo FLASH sequence (see Section 2.2.5 ).

Whole-body MR systems with lower field strength (1.5 T) often do not have specific shim coils and are limited to first-order shims. At higher field strength (≥3 T), second-order shim coils are standard in most MR systems (see Figure 2.2.6 ), and at 7 T or beyond at least some third-order coils and sometimes even a few fourth-order coils are available. These coils are usually integrated in the gradient coil unit but have their own power supply. Some vendors also provide superconducting shim coils within the cryostate that are adjusted during the installation of the MR system to optimize the field homogeneity in the empty bore for the specific MR environment (“tune-up shim”). These coils are usually termed “cryo shims”, while the standard shim coils are often referred to as “room-temperature shims”.

Even with higher-order shim coils, the complex field variations that can be present in a target volume cannot be compensated completely. One option to overcome this limitation is the usage of local shim coils. For instance, small coils within the oral cavity can reduce signal losses in T ₂ ^∗ -weighted functional neuroimaging of the orbitofrontal cortex. For optimum results, local shim coils should be designed to meet the specific needs of the target region. However, with a few coils of different designs that can be positioned and adjusted independently, a quite good compensation can be achieved as has been demonstrated for the human brain. This solution could be adapted for spinal cord applications to reduce larger-scale inhomogeneities (e.g., as caused by the lung).

A promising extension involves a fixed array of small coils that can be controlled independently. A setup of 24 coils around the mouse head has been successfully tested on an animal MR system and has been shown to be able to generate a variety of field variations, including third-order terms. Interestingly, it can also provide linear field gradients along any direction, which could be used to perform the spatial encoding rather than using a dedicated gradient coil. Recently, a first setup for the human head consisting of 48 coils has been developed and has been shown to improve shimming of the human brain at 7 T compared to the standard shim setup involving third-order shim coils. Thus, it seems to be very promising to apply this concept to the human spinal cord because it could also be able to address some of the periodic field variations caused by the vertebrae. However, an issue that needs to be considered is RF coupling of the local shim coils that may distort and reduce the RF field.

2.2.3.2

Passive Shim

For passive shimming, ferromagnetic, paramagnetic, or diamagnetic materials are positioned in the bore of the magnet in order improve the field homogeneity in a target region. The simplest realization is to reduce or remove the susceptibility differences that cause the field inhomogeneities, in particular by replacing air in or around the body by a material with a magnetic susceptibility close or equal to that of tissue, such as water ( Figure 2.2.7 (A) ) or a foam of pyrolytic graphite (volume fraction 5%). Regarding the spinal cord, this approach could be applied to reduce effects occurring at the body’s surface, but it may interfere with the need to position surface coils as close as possible to the target volume to maximize the signal-to-noise ratio. Furthermore, it is unable to address the usually more pronounced susceptibility differences caused by bones and the air-filled lung.

(A) Example for a simple passive-shimming approach in a water phantom acquired with T ₂ ^∗ -weighted echo-planar imaging. Two different slices close to the bottom of the phantom (top) and about 30 mm apart from the bottom (bottom) are shown, with the phantom alone in the bore where the bottom represents an air–phantom boundary with a considerably difference of magnetic susceptibilities (left), and with a second water phantom attached to the bottom of the first such that no significant difference of magnetic susceptibilities is present (right). The latter setup reduces signal losses and geometric distortions significantly. (B) Examples for the improvements in T ₂ ^∗ -weighted echo-planar imaging achievable with a static shim involving first- and second-order room-temperature shims. Without an adjustment of the static shim (left), severe geometric distortions and pronounced signal losses occur. These artifacts are considerably ameliorated after an adjustment of the static shim (right).

In a more elaborated approach, dedicated amounts of a shim material with a magnetic susceptibility that differs from that of tissue (see Table 2.2.1 ) are positioned at different locations (see also Section 2.2.6 ) within the magnet bore or close to the target volume. To optimize the field homogeneity, the locations and quantities of the material must be carefully chosen (e.g., Refs ) and depend on the susceptibility of the material (see also Section 2.2.6 ). Due to the variety of locations that are usually available, more complex field corrections can be realized than with standard shim coils (e.g., Ref. ). To minimize the amount of shim material, only those higher-order field variations are usually corrected for which no room-temperature shim coils are available.

The type of feasible shim materials depends on the specific geometry and application. As a rule of thumb, the larger the distance to the target region is, the higher should be the difference of the material’s and the tissue’s susceptibilities (see Table 2.2.1 ). For instance, some vendors use passive shimming materials located around the tunnel to improve the field homogeneity of the empty bore for the specific MR environment as part of the “tune-up shim” during the installation or after major hardware upgrades. In this case, ferromagnetic materials (iron, nickel, cobalt, or alloys of them) are used to attain a significant field distortion in the isocenter (“iron shim”).

Several passive shim approaches have been presented that can be adapted to the specific target region investigated. In one variant, ferromagnetic materials have been used to shim the visual cortex of macaque brains. Such materials provide a high efficiency in distorting the field due to their excessive susceptibility and, thus, can provide significant corrections even deeper in the body. But attention must be paid to the considerable force and torque that may act on ferromagnetic materials within the static field. Thus, for adjusting the shim (i.e., the locations of the materials) in humans, either the subject or the shim device may have to be removed from the bore after the measurement of the field distribution for safety reasons. This would require time and a good reproducibility of the subject’s or the device’s position. However, this approach could provide a good solution to correct typical inhomogeneity patterns that are observed for a target volume independent of the subject. Thus, a fixed passive shim can be set up prior to the examination and used for different subjects.

For an individual, subject- or target-specific shim adjustment, high-susceptibility para- and diamagnetic materials, like graphite, bismuth, niobium, and zirconium (see Table 2.2.1 ), seem to be more feasible. They do not create safety issues, but their susceptibility is large enough to cause significant distortions even deeper in the body (e.g., in the human brain), if they are located close to the object. Thus, a subject- or even target-specific shim can easily be realized as has been demonstrated in animals and in the human brain, for example to reduce inhomogeneities in the orbitofrontal and temporal lobes by shim material located in the mouth or close to the forehead and ears. The usage of both dia- and paramagnetic materials (bismuth and zirconium) has been shown to yield better results and outperforms third-order room-temperature shims in the mouse brain at 9.4 T. An adaptation of such approaches to spinal cord applications could be very promising. As long as electrically conducting materials are used, their compatibility with the MR acquisitions must be ensured, for example regarding distortions of the RF field and the induction of eddy currents that could give rise to artifacts and could heat up the material and affect its magnetic susceptibility (i.e., the field correction).

2.2.4

Tune-up, Static, and Dynamic Shim

Several levels of shimming are usually applied to optimize the field homogeneity in the target region. During the installation of an MR system and after major hardware upgrades, the homogeneity of the magnetic field in the empty bore is optimized for the specific MR environment (“tune-up shim”). The setup of the corresponding shim components, the cryo shim coils and the iron shim (see Section 2.2.3 ), then remains fixed and cannot be adapted by the user. It therefore will not be considered here. The more flexible shim components like the room-temperature shim coils (see Section 2.2.3 ) can be adapted to correct the field distortions in the body part to investigate that, for example, are induced by the different magnetic susceptibilities of air, bones, and tissue. Usually, this setup is performed specifically for the chosen target volume and is fixed during the acquisition (“static shim”; Section 2.2.4.1 ), but dynamic approaches that aim to provide an optimized setup for different subvolumes, for example by updating the shim settings on a slice-by-slice basis, have also been presented (“dynamic shim update”; Section 2.2.4.2 ). Furthermore, (dynamic) pulse sequence modifications have been used to ameliorate the effects of field inhomogeneities, particularly in T ₂ ^∗ -weighted acquisitions. Strictly speaking, such techniques should not be considered as “shim” methods because they do not improve the field homogeneity but only aim to compensate the side effects that they have on the signal. Nevertheless, due to their relevance for spinal cord applications, they will be considered in the context of the applications for which they are useful (see Sections 2.2.8 and 2.2.9 ).

2.2.4.1

Static Shim

The field inhomogeneities in vivo depend on the body’s geometry and orientation in the bore and the distribution of bones and air within the body. Thus, a flexible correction of the actual inhomogeneities in the target volume, for example as determined from a field map (see Section 2.2.5 ), on an acquisition-by-acquisition basis is important.

On standard MR systems, this is realized using the gradient coil (first-order terms) and, if available, the room-temperature shim coils (second- and higher-order terms; see Section 2.2.3.1 ), but approaches with passive shims have also been proposed (see Section 2.2.3.2 ). While the room-temperature shim coils are independent of the hardware involved in the MR acquisitions, the gradient coil is also used for the spatial encoding. Thus, the static current offset applied to the gradient coil for shimming may reduce the maximum current available for pulsed gradients on the different axes (i.e., the specified gradient strength usually is not fully usable for pulsed gradients).

With the room-temperature shim coils, a relevant improvement of the field homogeneity can usually be achieved (see Figures 2.2.7(B) and 2.2.9 ), but higher-order field variations cannot be corrected appropriately. Thus, static, passive shim approaches (see Section 2.2.3.2 ) have been presented to improve the field homogeneity within the target region. They are suitable for correcting more complex field variations, but their feasibility to improve the homogeneity in the human spinal cord so far has not been demonstrated. Another option is local shim coils or coil arrays (see Section 2.2.3.1 ), that is, dedicated coils located within the bore close to the target region. So far, such devices are not commonly available but with an appropriately modified geometry could be quite helpful for spinal cord applications.

Only gold members can continue reading. Log In or Register to continue

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)

Related posts:

Traumatic Spinal Cord Injury: Acute Spinal Cord Injury and Prognosis Ultra-High Field Spinal Cord Imaging Array Coils T 2Relaxation Spinal Cord fMRI Single Voxel MR Spectroscopy in the Spinal Cord: Technical Challenges and Clinical Applications

Stay updated, free articles. Join our Telegram channel

Join