Magnetic Resonance Concepts

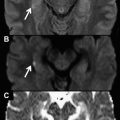
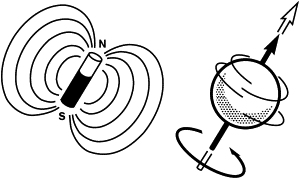
MR imaging works because, in the presence of an external magnetic field, one can measure the interaction between protons in human body and the external magnetic field itself. Protons interact with the external magnetic field, due to an intrinsic magnetic characteristic called spin. The classical view of spin is the effect of one charged particle—a proton, for example—spinning around itself, which creates a magnetic moment pointing perpendicularly toward a spinning axis ( Fig. 1 ). In the presence of an external magnetic field, this proton behaves similarly to a magnetic bar, tending to align to the field and precesses around it.

In the classical view, a charged particle with spin can be compared as a magnetic dipole such as a bar magnet.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

When we are dealing with individual protons, we need to look at them through “quantum mechanical glasses,” and “not-so-intuitive” thoughts are permitted under this treatment. A not-intuitive behavior is that this proton can align in either a parallel or an antiparallel orientation to the external magnetic field. There is a difference of energy between a parallel and an antiparallel state, and if this exact amount of energy is matched by an incident radiation and is delivered to the proton, it absorbs this energy and changes from one state to another. This phenomenon is called magnetic resonance. The difference of energy states depends on the magnitude of the external magnetic field B ₀ where this proton is inserted, and is expressed in terms of the Larmor equation (1) as:

In equation (1) , w ₀ is the frequency needed from the incident electromagnetic field to match the energy difference between states of nuclei, with the gyromagnetic constant y in the presence of an external magnetic field of amplitude B ₀ . The gyromagnetic constant y is an important nucleus characteristic. Human body abundance and proper gyromagnetic constant make hydrogen nuclei (H ⁺ ) the best choice for magnetic resonance imaging.

But in MR imaging, we are not dealing with a single spin and instead of a quantum mechanics view, a classical treatment can be used to understand MR imaging physics. In a classical mechanics view, spins in the presence of an external magnetic field B ₀ start to precess around B _0, with an angular frequency w ₀ ( Fig. 2 ). The precessional frequency is given by the same relationship expressed in quantum mechanics treatment, the Larmor equation.

Precession of spin axis around B ₀ .

( Courtesy of GE Healthcare, São Paulo, Brazil.)

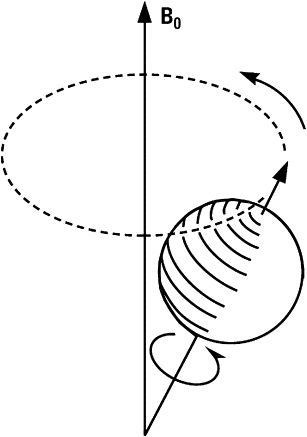
The sum of many spins rotating around B ₀ forms the magnetization vector M that points in the same direction as B ₀ . When RF wave in resonance frequency w ₀ irradiates the bulk of spins, the quantum effect of states transition is analogous to flip the vector M by a certain angle in relation to B ₀ . If RF in resonance frequency is applied by a certain time that flips the vector M 90°, this RF pulse is said to be a “90° RF pulse.” The same nomenclature applies to a “180° RF pulse.”

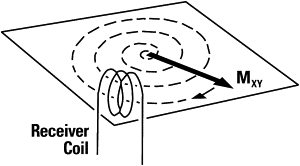
Consider the following experiment: a bulk of spins in the presence of external magnetic field B ₀ . At this time, the equilibrium time, vector M, possesses only the longitudinal component M _z . A 90° RF pulse is applied. After turning RF off, vector M has only the transversal component M _xy and under the influence of B ₀ starts to precess around it. At this time, vector M induces current in the receiver coil, according to Faraday’s law of induction, and generates the MR signal ( Fig. 3 ). When it passes through the receiver coil a maximum signal is obtained, and when it is the farthest from the coil a minimal signal is obtained. Plotting signal versus time, a sinusoidal function is to be expected.

In the transversal plane, rotating magnetization vector M induces current in receiver coil according to Faraday’s law of induction.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

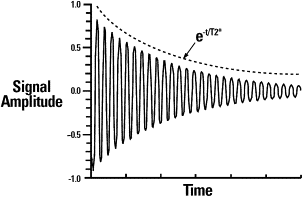
But instead of a simple sinusoidal function, a sinusoidal function with amplitude decrease over time is obtained ( Fig. 4 ). The signal represented in Fig. 4 is called FID (free induction decay), which decays due to a process known as relaxation.

MR signal amplitude (proportional to M vector magnitude) as function of time. The exponential damped sine function is called FID and is characterized by relaxation effect.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

Relaxation Effects

Signal relaxation is a result of loss of phase between spins and energy release to the environment where spins are inserted. Immediately after a 90° RF pulse, all spins that form the M _xy vector are pointing in the same direction, and they are said to be “in phase.” Turning RF off, they are set free to precess around B ₀ , and they precess with an angular frequency according to the Larmor equation. The first problem is that not all spins feel the same static field, due to B ₀ inhomogeneities, and as they feel differently, they precess with different frequencies. This difference causes a loss of phase between them and after some time carrying out vector addition, it can be understood why the signal vanishes ( Fig. 5 ). This process is called T2* decay or T2* relaxation, and effects of this nature can be restored once it is not a random effect but a scanner characteristic.

Signal loss due to dephasing between spins, caused by T2* and T2 relaxation.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

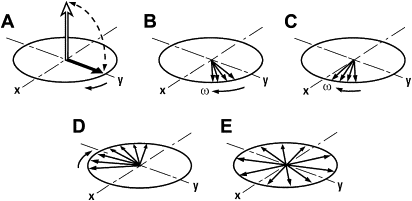
The same loss of phase described here can happen even though scanner B ₀ homogeneity is perfect. Spins that form vector M _xy can interact with each other, feeling the tiny magnetic field of neighboring spins, in addition to B ₀ , and each spin starts to precess with a different frequency, resulting in the same loss of phase caused by B ₀ inhomogeneities. The central difference is that this loss of phase cannot be recovered once thermal motion of spins is random. This process is called T2 relaxation or T2 decay. T2* and T2 decay express exponential behavior (see Fig. 4 ) and are modeled in terms of transversal components of vector M.

Another source of signal decay is spins giving up energy, which are absorbed by an RF pulse to the environment. In terms of magnetization vectors, vector M _xy decreases and M _z increases over time, until all energy has been released and the vector M has only a longitudinal component ( Fig. 6 ), returning to equilibrium. The energy exchange is governed by the interaction between spins and the lattice, and it is called T1 decay or T1 relaxation.

The decay of transverse magnetization occurs by means of T2 and T2* effects, while recovery of longitudinal magnetization reflects energy transference to the environment.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

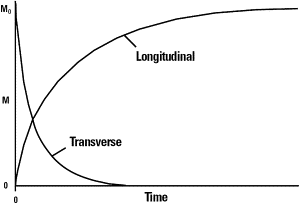
T1, T2, and T2* are tissue properties, and are measured in seconds (T2* carries B ₀ inhomogeneities information, caused by the tissue and the scanner). T1 is the time needed for M _z to achieve approximately 63% of its initial value, after a 90° RF pulse. T2 and T2* are the times taken for M _xy to achieve approximately 37% of its initial value, after a 90° RF pulse, T2* being measured taking into account inhomogeneity effects and T2 being measured taking into account only spin-spin interactions. Image contrast contains all relaxation effects, but usually they are weighted in one effect, meaning that differences in the gray scale mostly represent differences in tissue relaxation properties. Image weighting is controlled by pulse sequences.

Pulse Sequences

In the circumstance whereby the external magnetic field is not particularly uniform, dephasing between spins caused by field inhomogeneities are the main source of signal loss. Fortunately, this effect can be reversed by a well-known RF pulse sequence called the “spin echo method.”

The spin echo sequence is based on the application of 2 RF pulses: a 90° RF pulse (or excitation pulse) followed by a 180° RF pulse (or refocusing pulse). The 90° RF pulse tips all spins that form the vector M into a transversal plane and immediately after they reach the plane, they are in phase and M _xy has its maximum amplitude. After turning the RF pulse off, spins start to precess and lose phase by T2* relaxation effects. The 180° RF pulse is applied after a time t, defined as t = TE/2 (t is set equal to 0 at the time the first 90° RF pulse is applied), rotating the spins by 180° in relation to the position they were in. At the end of refocusing the pulse application, the spins localization remains in the transversal plane, but “faster” spins with higher precessional frequency are put behind “slower” spins with lower precessional frequency. The accumulated phase between spins caused by field inhomogeneities through the time from t = 0 seconds to t = TE/2 seconds is compensated after a 180° RF pulse at the time t = TE seconds (called echo time), TE/2 seconds after refocusing pulse. The whole picture is better understood in Figs. 7 and 8 .

The mechanism of spin echo with application of 180° RF pulse.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

A spin echo experiment with acquisition of 2 echoes.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

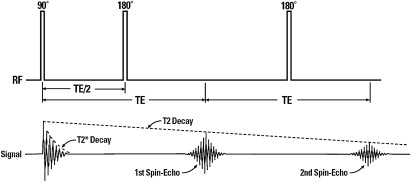
The realignment of spins is called spin echo. It is possible to apply many refocusing pulses after a 90° RF pulse, collecting many spin echoes as shown in Fig. 8 . B ₀ inhomogeneities are canceled in this method, because they are static in time, and the same B ₀ inhomogeneity that spins feel before refocusing pulse they also experience after it. But spin-spin interactions are not static in time and T2 decay cannot be avoided. The longer the time a spin echo is collected, the stronger a T2 relaxation effect is presented.

Another important figure in pulse sequence is the repetition time TR, the time between 2 excitation pulses. In the spin echo sequence, TR is the time between 2 90° RF pulses applied in the same location.

TR and TE are the main parameters in spin echo sequence used to control contrast image weighting. Signal is acquired in echo time t = TE, and according to parameters set in the sequence, the spin echo received in the receiver coil will express differences among tissues, regarding proton density (PD), and T2 or T1 relaxation.

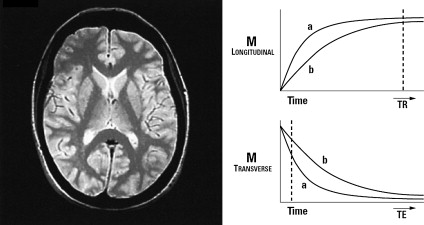
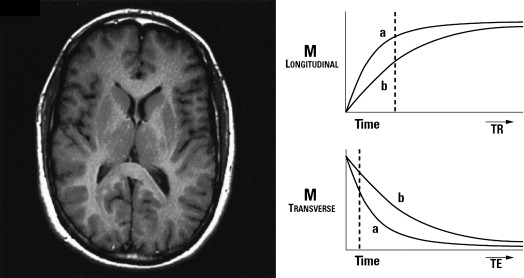
Consider 2 different magnetization vectors, M _a and M _b, possessing different PD, T1, and T2 properties. At equilibrium state, M vector magnitude depends on PD available in the tissue. A 90° RF pulse is applied in the system, and M _a and M _b relay into the transversal plane. Dephase between spins starts at different rates, and a refocusing pulse is applied at TE/2 to provide a spin echo at TE. If TE is short enough, T2 differences will not be relevant and the signal induced in the receiver coil will mostly represent PD properties. To fulfill this requisite, TR must be kept long enough, to allow M vectors to recover all their longitudinal magnetization and so that T1 differences will not influence M _xy vector after the next excitation pulse ( Fig. 9 ). Therefore, PD-weighted images acquired with a spin echo sequence are obtained by using long TR and short TE.

Proton density–weighted image acquired using long TR and short TE.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

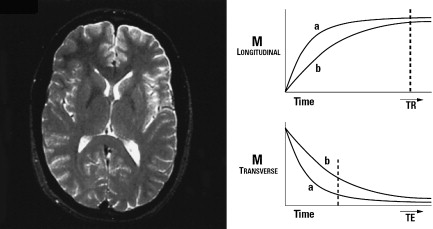
If a T2-weighted image is desired, a long TR is needed to avoid T1 influence through excitation pulse repetitions, but TE must be adequate to reflect T2 relaxation differences in signal amplitudes acquired ( Fig. 10 ). The optimal TE to optimize contrast between M _a and M _b is the time when the difference between transverse magnetization of M _a and M _b is larger. Therefore, T2-weighted images acquired with a spin echo sequence are obtained by using long TR and adequate TE.

T2-weighted image acquired using long TR and adequate TE.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

To acquire T1-weighted images, a short TE is needed for a signal echo not to reflect T2 differences. After applying the first excitation pulse, M _a and M _b remain in a transversal plane and dephasing between spins is caused by T2* relaxation effects. The refocusing pulse is applied at a short TE/2 time and the first echo acquired represents PD differences. Then, T1 relaxation effects become significant and M _z recovery starts to M _a and M _b . In order that all the following echoes represent T1 differences, TR must be adequate and optimize T1 image contrast between M _a and M _b , and the next excitation pulse must be applied at the time when longitudinal magnetization M _a and M _b is larger ( Fig. 11 ). Therefore, T1-weighted images acquired with spin echo sequences are obtained by using adequate TR and short TE.

T1-weighted image acquired using adequate TR and short TE.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

Gradient echo (GRE) is another important pulse sequence that, instead of using RF pulses to refocus spins, uses a gradient pulse, referring to a controlled linear change of magnetic field strength during a short period. The gradient is characterized by its amplitude, representing how much field strength has changed in a certain distance, and its polarity, representing the direction of the change in field strength.

In a GRE experiment, an excitation and 2 gradient pulses are applied with different polarities and duration. The first gradient pulse is applied after the excitation pulse. While the first gradient is turned on the magnetic field amplitude changes regarding spatial location, and spins precess at different frequencies according to the Larmor equation, causing a certain phase accumulation between them, and the signal diminishes. The first gradient is then turned off and the second gradient is turned on, with the same amplitude and different polarity. Spins forced to precess slower than that feeling B ₀ , in the presence of the first gradient, now are forced to precess faster in the presence of the second gradient and, after some time, the accumulated phase between spins is compensated by inducing a signal echo generated by a gradient: a “gradient echo.”

B ₀ inhomogeneities are not canceled in this method, because a gradient echo is acquired by manipulating the magnetic field, and the magnetic field felt by spins at the application of the first gradient is not the same in the presence of the second gradient.

Frequency and Phase Encoding

Pulse sequences are not used just to obtain different image contrasts but also to manipulate the spins and form an image. This manipulation is performed by turning gradients on and off, inducing phase and frequency for the spins, and using these properties as spatial information. GRE pulse sequence is used in the following explanation of image formation.

In a GRE pulse sequence, after the emission of excitation pulse, a gradient called “readout gradient” is applied, firstly with a negative polarity (to sample high frequencies of symmetric signal) and afterwards with a positive polarity to place spins in phase and read the echo. When this readout gradient, also known as frequency encoding gradient, is applied, H ⁺ spins precess at different frequencies at the same time the axis gradient was applied ( Fig. 12 ).

During the application of a gradient, the magnetic field is modified linearly across the application direction. This change in magnetic field implies a change in precessional frequency, according to the Larmor equation.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

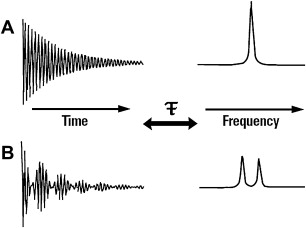
Although the signal induced in the receiver coil contains all frequencies emitted by the tissues, there is a mathematical tool called Fourier transform ( Fig. 13 ) that decomposes this signal in phases and frequencies. With the frequencies contained in the signal and the previous knowledge of the readout gradient amplitude applied, it is possible to correlate signal frequency and spatial location toward an applied gradient.

The Fourier transform indicates the frequencies contained in the signal.

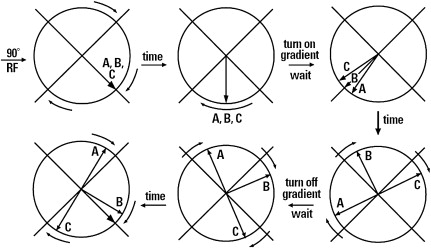
Unfortunately, it is not possible to apply the same strategy in the other axis, because it would change the spins frequency twice and only the last result would be obtained. To apply another gradient in other direction simultaneously would not be a solution, because magnetic fields would be vector summarized and just one frequency gradient would result. To solve this problem, phase information of spins is used. This information is added by applying a gradient called the “phase-encoding gradient” before the readout gradient and perpendicular to it. The phase-encoding gradient is kept for a short period to modify the magnetic field in the gradient direction, and during this short period spins precess at different frequencies according to equation (1) . When the phase-encoding gradient is turned off, spins precess at the same frequency again, but they keep the phase memory acquired in the presence of the gradient ( Fig. 14 ). The accumulated phase between spins depends on the gradient amplitude and duration.

Phase-encoding scheme representing 3 spins at different locations.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

In the sampling time, each part of the subject to be imaged will possess a bulk of spins with different phase and frequency information, making possible the image formation. The pulse sequence cycle must be repeated until K-space is filled in a proper way to form the final image.

K-Space and Acquisition Time

After frequency and phase encoding, a continuous signal emitted by the object to be studied is received by the receiver coil and sampled by the equipment, becoming a discrete signal. The signal sampled is converted in voltage and organized in the K-space, which holds the raw data of the image. As the signal is encoded in phase and frequency, both are the coordinates of K-space ( Fig. 15 ). The inverse Fourier transform of K-space signal magnitude is the usual magnetic resonance image, thus a good coverage of K-space is needed to guarantee a reasonable image quality.

Image formation by phase and frequency encoding using Fourier transform. ( A ) Slice representation with 3 vials of water. ( B ) Spin echo acquired from the entire slice with different phase encoding. ( C ) Fourier transformation of the signal. ( D ) A new data set is assembled from the columns in ( C ). ( E ) Inverse Fourier transform of ( D ) produces the image.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

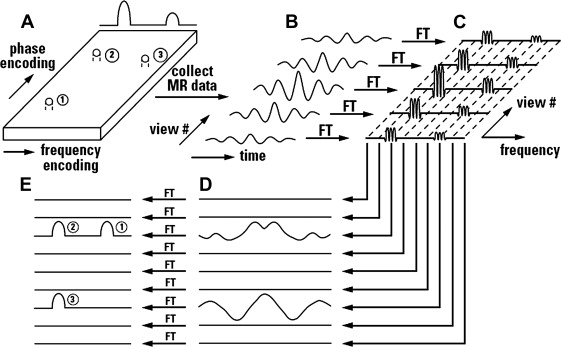
Pulse sequence controls K-space coverage. The phase-encoding gradient indicates the starting line in K-space to signal sampling, and the frequency-encoding gradient indicates the sampling direction on this line. Refocusing pulses to echo acquisition inverts the sampling direction.

The number of sampled points in K-space must be higher or equal to the number of pixels that compose the final image, thus pulse sequence must be repeated n times, varying the phase-encoding gradient amplitude to the entire coverage of K-space, where n corresponds to the matrix value in the phase direction; this is the first factor that hampers image acquisition time. The frequency encoding does not have a significant impact in acquisition time, because it takes the readout gradient duration (on the order of milliseconds). Nevertheless, the phase encoding to receive one echo depends on the application of one RF pulse, and TR must be taken into account for image contrast. Therefore, TR and phase-encoding steps are primarily the main aspects that affect image acquisition time, and usual methods that optimize acquisition time are multislice acquisition (excitation of multiple slices inside a TR) and acquisition of multiple phase-encoding steps inside a TR, using either RF pulses or readout gradients, between phase-encoding steps.

Principles and Concepts

Diffusion refers to the transport of gas or liquid molecules through thermal agitation randomly, that is, it is a function of temperature above 0 K. In pure water, collisions between molecules cause a random movement without a preferred direction, called Brownian motion. This movement can be modeled as a “random walk,” and its measurement reflects the effective displacement of the molecules allowed to move in a determined period. The random walk is quantified by an Einstein equation: the variance of distance is proportional to 6Dt , where t is time and D is the proportionality constant called the diffusion coefficient, expressed in SI units of m ² /s.

According to Fick’s law, diffusion also occurs from a region of higher concentration to a lower concentration.

In biologic tissue, there is a high probability that water molecules interact with structures such as cell membranes, macromolecules that reduce or impede its motion ( Fig. 16 ). Water exchange, between intracellular and extracellular compartments, as well as the shape of extracellular space and tissue cellularity, affects diffusion. In this case, the term apparent diffusion coefficient (ADC) represents the measured diffusion constants and is commonly reported in cm ² /s or mm ² /s.

( A ) Water molecules travel by “random walk” more freely than ( B ), as the freedom of this movement is reduced by barriers as cell membranes. The diffusion in ( B ) is restricted as compared with ( A ). Finally, ADC ( B ) is less than ADC ( A ).

( Courtesy of GE Healthcare, São Paulo, Brazil.)

Isotropy and anisotropy

Isotropy means uniformity in all directions. A drop of ink placed in the middle of a sphere filled with water spreads over the entire volume, with no directional preference. If the same experiment is repeated in a sphere filled with uniform gel the restriction is increased as compared with free water, but is still isotropic, as the restriction is the same in all directions.

Anisotropy implies that the property changes with the direction. If a bundle of wheat straw with the fibers parallel to each other is placed inside a glass of water, the ink will face severe restriction in the direction perpendicular to the fibers and facilitated along the fibers. This bundle is highly anisotropic ( Fig. 17 ).

The bundle offers no resistance to water molecules in the diffusion direction parallel to the fibers but there is a severe restriction if perpendicular. In this case there is preferred water molecule direction due to anisotropy. Outside the bundle, the water molecules are in an isotropic environment and have no preferred direction.

( Courtesy of GE Healthcare, São Paulo, Brazil.)

Diffusion-Weighted Imaging

MR image contrast is based on intrinsic tissue properties and the use of specific pulse sequences and parameter adjustments. The image contrast is based on a combination of tissue properties and is denominated “weighted,” as the contribution of different tissue properties are present, but one of them is more expressive than the others.

Routine acquisitions have some degree of diffusion influence that is actually quite small. Some strategies have been developed to make diffusion the major contrast contributor, and dedicated diffusion-weighted imaging (DWI) sequences are available nowadays on commercial scanners, as well as several others as investigational sequences that may or not be available in clinical practice.

Diffusion sensitization scheme

Stejskal and Tanner introduced a method to image and quantify DWI with MR imaging in 1960, which was implemented in routine practice by Le Bihan and colleagues in 1986. The sequence was based on a spin echo sequence that has symmetric diffusion sensitizing gradients inserted before and after the 180° refocusing pulse ( Fig. 18 ). The idea is as follows.

Stejskal-Tanner Scheme: 2 diffusion-sensitizing gradients inserted before and after 180° RF refocusing pulse using precisely controlled duration and distance. G, amplitude; δ, duration of the sensitizing gradient; Δ, time between the 2 sensitizing gradient lobes.

Static water spins will experience a precise dephase induced by the first diffusion sensitizing gradient lobe. The 180° pulse will cause a phase compensation for the external field inhomogeneities. The second lobe will rephase the water spins at the same amount they were dephased, as the area is exactly the same and spins were in the same position. Therefore, the signal of the stationary water spins echo is maintained as practically unaltered.

However, moving water spins will be in a different position, so they will not be rephased at the same amount by the second lobe, and the echo will have a reduced signal. The degree of water motion is proportional to the signal attenuation.

The diffusion-sensitizing gradients can be applied to x, y, or z axes, as well as in a combination of them. This direction is called the diffusion-sensitizing direction.

The Stejskal-Tanner scheme can be applied on top of pulse sequences as spin echo, but the most used nowadays is in combination with spin-echo echo-planar imaging (SE-EPI). A combination with fast spin echo sequence takes longer, but is less sensitive to distortions and susceptibility artifacts than EPI.

Other strategies are also available but are less used in routine practice, as many others are in the research environment and become commercialized eventually.

Diffusion-weighting factor

The sensitivity of the diffusion sequence to water motion can be varied by changing the gradient amplitude, the duration of the sensitizing gradients, and the time between the gradient pair.

The diffusion-weighting factor is named b-value and for the Stejskal and Tanner sequence the value is given in units of s/mm ² by (2) :

<SPAN role=presentation tabIndex=0 id=MathJax-Element-2-Frame class=MathJax style="POSITION: relative" data-mathml='b=γ2.G2.δ2(Δ−δ/3)’>b=γ2.G2.δ2(Δ−δ/3)b=γ2.G2.δ2(Δ−δ/3)
b = γ 2 . G 2 . δ 2 ( Δ − δ / 3 )

Only gold members can continue reading. Log In or Register to continue

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)

Related posts:

Diffusion Magnetic Resonance Imaging in the Head and Neck Diffusion MR Imaging in Central Nervous System Diffusion-Weighted Magnetic Resonance Imaging in the Upper Abdomen: Technical Issues and Clinical Applications Pelvic Applications of Diffusion Magnetic Resonance Images Diffusion-Weighted Imaging of the Chest Diffusion-Weighted Magnetic Resonance Imaging for the Evaluation of Musculoskeletal Tumors

Stay updated, free articles. Join our Telegram channel

Join