Fig. 1
Estimation of radiation-induced second-cancer risks based on a dose-volume histogram (DVH). The DVH (a) is for the left breast of a female treated for breast cancer by radiotherapy; the doses are in 0.5 cGy intervals. b The estimated contribution of different dose intervals within the irradiated breast to the overall excess relative risk (ERR), assuming the dose–response relationship for the ERR is approximately linear in dose
A reasonable approach to minimizing radiation-induced second cancers would be to compare radiotherapy protocols of equal efficacy against the primary tumor, and identify the ones with the lowest second cancer risk. However, because the latency period for radiation-induced solid tumors is long (Curtis et al. 2006; Brenner et al. 2000; BEIR VII Report 2005; Ivanov et al. 2004), the carcinogenic effects of radiotherapy have been directly measured only for regimens used several decades ago. The risks which may be associated with newer treatment methods are for the most part not yet observable. Biologically motivated mathematical/computational models, calibrated using data from older protocols, can address this problem by predicting risks of current (and prospective) treatment regimens.
A systematic review of the epidemiological data on second cancers has been given in the chapter titled “Understanding and Predicting Radiation-Associated Normal Tissue Injury: A Global and Historical Perspective”. Here, we discuss some biologically based models of spontaneous and radiation-induced carcinogenesis in the literature, and analyze their potential for predicting second cancers due to modern treatment protocols. Most of the discussion focuses on solid tumors. Leukemias, which can be substantially different from solid tumors in terms of latency period and dose–response relationships, are treated separately. We also discuss an example of a potentially useful approach for improving biologically based second cancer modeling by unifying some current model concepts to produce a formalism which includes both short- and long-term mechanisms important for radiation carcinogenesis.
2 Short-Term Biologically Based Models
Biologically motivated mathematical modeling of spontaneous and ionizing radiation-induced carcinogenesis has a history spanning more than 50 years (Nordling 1953; Armitage and Doll 1954). Many biologically based models can be characterized as short–term, in that they focus on those processes occurring during and shortly (i.e., about 1 month or less) after irradiation (Sachs and Brenner 2005; Nilsson et al. 1990; Thames 1985; Dale 1986; Sontag 1997; Lange et al. 1997; Zaider and Wuu 1995; Stewart 2001; Curtis 1986; Tobias 1985; Radivoyevitch et al. 2001; Hahnfeldt and Hlatky 1996, 1998; Mebust et al. 2002; Schollnberger et al. 2002; Hofmann et al. 2006; Sachs et al. 2007; Shuryak et al. 2006; Little 2007; Schneider and Kaser-Hotz 2005; Schneider and Walsh 2008). These models typically analyze the induction of short-term endpoints which are used as surrogates for carcinogenesis, such as mutations or chromosome aberrations (Radivoyevitch et al. 2001; Ottolenghi et al. 1999). Different short-term models analyze DNA damage induction and DNA repair/misrepair (Nilsson et al. 1990; Sontag 1997; Stewart 2001; Curtis 1986; Tobias 1985). Short-term models take into account a variety of phenomena such as dose rate effects (Thames 1985; Rossi and Kellerer 1986; Brenner et al. 1996), induction and/or saturation of particular repair pathways (Schollnberger et al. 2002), and alterations of the cell cycle distribution during/after irradiation (Zaider and Wuu 1995; Hahnfeldt and Hlatky 1996, 1998). Many short-term models are motivated toward radiation-induced cancer risk estimation at low radiation doses (Bennett et al. 2004), but some have also been adapted to predict radiotherapy-induced second cancers (Dasu et al. 2005; Dale 1986; Schneider and Kaser-Hotz 2005; Schneider and Walsh 2008). The common feature of these short-term models is that the long-term processes involved in carcinogenesis, which are dominant before radiation exposure and in the long latency period after initial tissue recovery from radiation damage, are typically treated indirectly, nonmechanistically, or not at all. Often a proportional hazards assumption is used to justify taking the shape of the cancer incidence dose–response curve as being the same, apart from an overall scaling factor, as the shape of the dose–response curve for some short-term surrogate endpoint (BEIR VII Report 2005; Upton 2003; NCRP Report 136 2001).
The main advantage of this class of models is that they provide a detailed initial dose response for short-term endpoints which are used as surrogates for carcinogenesis. The main disadvantage is that the possibly substantial modulations of the magnitude and shape of this initial dose response during the lengthy period (multiple years-decades in humans) between irradiation and manifestation of typical solid tumors are not considered; a simple proportional hazards assumption, plausible at low doses, becomes questionable at the high doses responsible for some second cancers.
Among the great variety of mathematical formalisms which can be classified as short-term radiation carcinogenesis models, we here focus on those models designed specifically for analyzing radiotherapy-induced second cancers.
2.1 The Linear Quadratic Exponential Model
The assumption that radiation-induced carcinogenesis is primarily governed by a balance of cell mutation (also commonly referred to as initiation) and cell killing (often referred to as inactivation) has been used for many years (Gray 1957). It has generally been quantified by use of the so called linear-quadratic-exponential (LQE) equation. This equation uses the classic linear-quadratic form both for radiation induced initiation (i.e., a D + b D 2, where D is radiation dose and a and b are adjustable parameters) and for radiation-induced inactivation (exp[− α D − β D 2], where α and β are adjustable parameters). It has been applied to data from Japanese atomic bomb survivors (Bennett et al. 2004), and to radiotherapy-treated cancer patients (Dasu et al. 2005).
At very low doses (≪1 Gy), the quadratic terms for both initiation and inactivation in the LQE equation are negligible, given realistic parameter values. The dose response is, therefore, effectively linear. This qualitatively agrees with the linear-no-threshold (LNT) approach generally used for radiation protection estimates at low doses (BEIR VII Report 2005; NCRP Report 136 2001). At intermediate radiation doses (i.e., up to a few Gy), the equation predicts that the radiogenic cancer risk is an increasing function of dose. This is because at such doses the risk is dominated by initiation, and inactivation has a limited effect since the majority of cells can survive the exposure. At high doses (e.g. ≫5 Gy), however, the exponential inactivation term leads to a very small predicted radiogenic risk, because essentially all radiation-initiated cells would be inactivated by the radiation. These model behaviors are illustrated graphically in Fig. 2, for both single and for fractionated radiation doses.
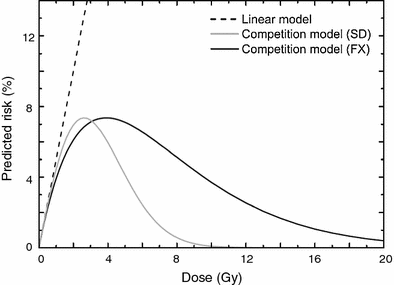

Fig. 2
Typical dose responses for radiogenic cancer risk predicted by the LQE model involving competition between cell mutation and killing for single radiation doses (SD) and fractionated doses (FX), using the same parameters. A strictly linear dose response that neglects cell killing is shown for comparison. The figure is reproduced from Dasu et al. (2005)
2.2 Semi-Empirical Models with Cell Proliferation
The LQE model often underestimates the risks of high radiation doses (Sachs and Brenner 2005), presumably because it describes only the processes of cell initiation and inactivation. A biologically plausible explanation for the persistence of large risks at high fractionated doses delivered during cancer radiotherapy is that cell proliferation during the time intervals between dose fractions and shortly after treatment stops negates much of the effect of cell inactivation. The recent models by Schneider and Kaser-Hotz (2005), Schneider and Walsh (2008) address this issue by providing a semi-empirical or phenomenological treatment of cell proliferation (and possibly other relevant factors that alter the dose response at high doses) by means of the following alternative assumptions:
(1)
A linear-exponential model, which assumes that the dose response consists of a linearly increasing term and an exponentially decreasing term. The linearly increasing term can be interpreted as a combination of all the factors leading to cell initiation, and the exponentially decreasing term can be interpreted as the combination of cell inactivation and proliferation, along with possible other contributing factors. At low doses, the predicted risk grows approximately linearly. At higher doses it turns over, and tends to zero at very high doses.
(2)
A phenomenological plateau-dose model, which assumes that the dose response grows linearly at low doses and saturates at high doses by asymptotically approaching a plateau. The plateau can be interpreted as a balance of inactivation and proliferation, which tend to equilibrium by cancelling each other. The main difference from the linear-exponential model is that this formalism predicts a substantial radiogenic cancer risk even at very large doses.
One or other of these alternative models can potentially be applied to any dose distribution if the dose-volume histogram is available. They can also be used to calculate the organ equivalent dose (OED), which is defined as the integral of the dose-volume distribution weighted by the predicted cancer risk (Schneider and Kaser-Hotz 2005; Schneider and Walsh 2008). For a strictly linear dose response, OED is proportional to mean dose. For inhomogeneous dose distributions, it may differ considerably from the mean dose. Best fits of the two model versions to data on atomic bomb survivors and patients treated with radiotherapy for Hodgkin’s disease are shown in Fig. 3. This approach describes the atomic bomb survivor and second cancer data adequately and is potentially useful for additional second cancer risk estimation.
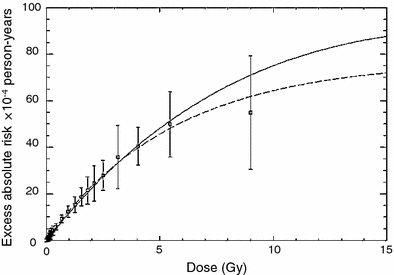

Fig. 3
Predicted cancer incidence as a function of organ absorbed dose of the atomic bomb survivors (squares). Shown are the fits to the combined dataset of A-bomb survivor data and Hodgkin’s patients using a linear-exponential model (solid line) and a plateau-dose model (dashed line). The data and fits are presented for a neutron RBE of 10. The figure and caption are reproduced from Schneider and Walsh (2008)
2.3 Initiation, Inactivation, and Proliferation Models
In contrast to phenomenological models, the so called initiation, inactivation, and proliferation (iip) models (Lindsay et al. 2001; Sachs and Brenner 2005; Sachs et al. 2007; Shuryak et al. 2006; Little 2007; Wheldon et al. 2000) involve a relatively detailed mechanistic treatment of the three short-term processes that give the models their name throughout the course of a typical high-dose (tens of Gy) fractionated radiotherapy regimen, and during a subsequent tissue recovery period of a number of weeks.
The model developed by Wheldon and Lindsay (Lindsay et al. 2001; Wheldon et al. 2000) is based on familiar two-stage concepts: Normal stem cells can be mutated to a pre-malignant (initiated) state, either spontaneously or by radiation. These once-mutated cells can, with a certain probability, acquire the second mutation, which makes them fully malignant. In addition to elevating the initiation rate, radiation can inactivate (kill, i.e., reproductively sterilize) both normal and initiated cells.
A key concept in the model involves compensatory proliferation of both normal and initiated cells after some of these cells have been inactivated by radiation. This process is assumed to occur in response to intercellular signals, restoring the homeostatically controlled total number of stem cells in the organ which existed before irradiation. Partial or complete impairment of the homeostatic mechanism by radiation is allowed in the model: Under complete impairment, no proliferation occurs after cell killing, and under no impairment surviving cells repopulate to exactly the same number, as was present before exposure. Intermediate scenarios are easily accommodated. The proliferation rate of initiated cells relative to normal ones is also treated as an adjustable parameter. They can proliferate as fast as, faster than or slower than normal cells. The model is mainly deterministic, but an approximation for stochastic extinction of all initiated cells after high doses of radiation is made. If all initiated cells in the organ are killed, then only normal cells participate in repopulation.
Typical radiation dose responses generated by the Wheldon-Lindsay model are shown in Fig. 4. The figure demonstrates the following important consequence of detailed modeling of cell proliferation in addition to initiation and inactivation: If compensatory cell proliferation is not accounted for, cell inactivation by radiation begins to overpower cell initiation at relatively low radiation doses of a few Gy. At higher doses (e.g., 10 Gy), predicted radiogenic cancer incidence would therefore quickly decline. However, cell proliferation stimulated by homeostatic mechanisms can compensate for much of the cell killing. So when proliferation is taken into account, radiogenic cancer incidence remains high even at doses >10 Gy. The latter situation is supported by some recent epidemiological data on radiotherapy-induced second cancers (Travis, the chapter titled “Understanding and Predicting Radiation-Associated Normal Tissue Injury: A Global and Historical Perspective” this volume, and Curtis et al. 2006; Sachs and Brenner 2005; Travis et al. 2002, 2003). Therefore, modeling cell proliferation of normal and initiated cells appears to be an important component of reasonably predicting the risks of second malignancies caused by radiotherapy for existing tumors.
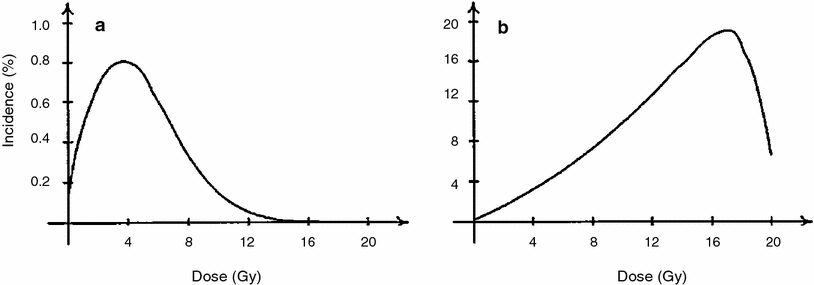

Fig. 4
The percentage incidence of carcinogenesis 20 years after irradiation is illustrated for a no cell repopulation and b full cell repopulation to 108 cells, using the Wheldon-Lindsay model. The figure and caption are reproduced from Wheldon et al. (2000)
The iip modeling approach for solid tumors was further refined by Sachs and Brenner (2005). Here a typical fractionated dosing radiotherapy regimen was modeled, and the iip processes were tracked in detail throughout the radiotherapy and subsequent tissue recovery periods. In particular, cell proliferation of both normal and pre-malignant cells was calculated in the time gaps between dose fractions, as well as during a recovery period after radiotherapy ends. Eventual risk of cancer was assumed to be proportional to the number of pre-malignant (initiated) cells present after radiotherapy and recovery, by the time when homeostatic organ repopulation has been completed. The relevant proportionality constants were estimated by using data on atomic bomb survivors. The main adjustable parameter in the model was the relative proliferation rate of initiated cells compared with normal ones, there called r. The model was fitted to epidemiological data on lung and breast cancers in patients irradiated for Hodgkin’s disease. The fits were adequate, as shown in Fig. 5.
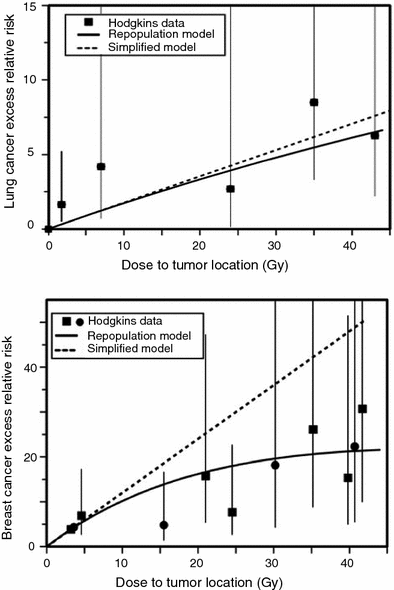

Fig. 5
Measured and predicted excess relative risks for lung cancer and female breast cancer induced by high doses of ionizing radiation, using the Sachs-Brenner iip model (solid curves). The data points are from studies of second cancers after radiotherapy of Hodgkin’s disease patients. The dashed lines are the predictions of the simplified repopulation model based on the slope at low doses derived from the excess relative risks of the atomic bomb survivors. The figure and caption are reproduced from Sachs and Brenner (2005)
The fits shown in Fig. 5 were produced using the relative proliferation rate of initiated cells compared with normal ones of r ≤ 1, e.g., r = 0.8. If r was >1, the model generated cancer excess relative risk (ERR) curves that increase faster than linearly with radiation dose, which was contrary to the data. This means that the model successfully describes the data only if initiated cells have a growth disadvantage during the tissue recovery period, rather than an advantage, which contrasts with the more commonly made assumption of clonal expansion. One explanation could be that the growth disadvantage occurs only on the relatively short-term time scale of a few weeks-months during and after radiotherapy, for example because some initiated cells could be selectively eliminated during interactions with surrounding normal cells. On the long-term time scale of multiple years on the pathway towards cancer, this disadvantage could disappear and a small growth advantage for initiated cells could emerge.
An alternative explanation is that the slope of the cancer ERR dose–response relationship is reduced at high doses by stochastic effects, i.e. due to stochastic extinction of a substantial proportion of initiated cells during radiotherapy. This possibility was explored in a stochastic extension of the deterministic iip model (Sachs et al. 2007). Indeed, it was found that, with realistic parameter values, stochastic effects due to cell killing during radiotherapy could be substantial. The variance of the number of live initiated cells after the multifraction radiotherapy protocol was typically much larger than the mean, and the probability that the simulated organ contains zero such cells after repopulation has run its course was quite high. This stochastic model allowed the epidemiological second cancer data to be fitted well even if a growth advantage for initiated cells was present during the recovery period (i.e., r > 1). It showed that reducing the overall radiotherapy treatment time, e.g., by treating on weekends, can reduce the second cancer risk by increasing the probability of stochastic extinction of pre-malignant clones.
3 Long-Term Biologically Based Models
By contrast with the short-term models described so far, another class of biologically motivated quantitative models can be characterized as long–term, in the sense that they track carcinogenesis mechanisms throughout the entire human or animal life span, e.g., the Armitage-Doll model (Armitage and Doll 1954; Armitage 1985), the Moolgavkar-Venzon-Knudson two-stage clonal expansion (TSCE) model (Moolgavkar 1980; Moolgavkar 1978; Moolgavkar and Knudson 1981), the two-stage logistic (TSL) model (Sachs et al. 2005), and many others (Little and Li 2007; Little and Wright 2003; Pierce and Mendelsohn 1999; Pierce and Vaeth 2003; Ritter et al. 2003; Yakovlev and Polig 1996). The main advantages of long-term models are: (1) including the modulation of the radiation dose response during the long latency period between radiation exposure and diagnosis of cancer; and (2), the fact that radiation carcinogenesis is usually treated as just a perturbation of background carcinogenesis, so that extensive data on spontaneous cancers can be used to help determine the adjustable parameters needed to estimate cancer risks. The main disadvantage is that the early radiation response is typically treated in a less-mechanistic, more phenomenological, manner than in the short-term models, and similarly for the dose-rate response. This disadvantage can be partially alleviated by suitable semi-mechanistic assumptions about the short-term aspects of the dose response, e.g., the effects of cell repopulation which partially compensates for cell killing by radiation (Heidenreich and Hoogenveen 2001), cell–cell interactions which can accelerate the proliferation of pre-malignant cells causing radiogenic promotion, etc. Some examples of long-term models that are relevant or potentially relevant to second-cancer estimation are discussed below.
3.1 Multistage Models Without Clonal Expansion
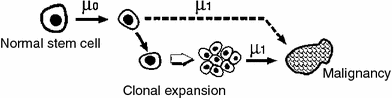
This class includes the earliest of the commonly used mathematical models of carcinogenesis—the pioneering models of Nordling (1953) and Armitage and Doll (1954). They are based on the concept that cancer originates from an ancestral target somatic cell, whose lineage has accumulated several relevant alterations (i.e., changes that are passed on to daughter cells). In current applications of these models, the target cells are usually thought of as organ-specific stem cells; the relevant alterations are thought to be mutations occurring in oncogenes and tumor suppressor genes, though chromosome rearrangements such as balanced translocations or inversions, copy number changes, or epigenetic changes are also sometimes discussed. Once a cell has accumulated all the necessary mutations, it becomes fully malignant, and can subsequently (after some lag period) develop into a clinical cancer. A pictorial representation of these models is provided in Fig. 6.
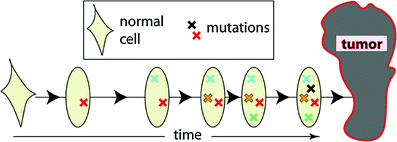

Fig. 6
A schematic representation of the assumptions for the Armitage-Doll model. The various mutations in the stem cell lineage produce pre-malignant changes. The last (black) mutation produces a fully malignant cell, which can grow into a tumor (grey mass)
Given realistic parameter values, the two models numerically behave very similarly over most of the human lifetime: they predict that cancer incidence should be approximated by a power function of age, where the power is equal to the number of necessary mutations minus one. When both age and predicted cancer incidence are plotted on a logarithmic scale, an approximately straight line is produced. These models fit the spontaneous age-dependent cancer incidence data for many adult-onset solid tumors reasonably well, particularly in the age range of 20–70. This observation led to the term “log–log cancers” (Moolgavkar 1986), referring to the fact that the age-specific incidence of these cancers can be described by a power function of age.
The number of mutations needed for full malignancy is usually considered an adjustable parameter in the Nordling and Armitage-Doll models. Fitting the models to spontaneous cancer incidence data suggests that this number is on the order of 5–6 for many solid tumors. This estimate agrees with experimental evidence in some cases (Tahara 2004; Tamura 2006; Midorikawa et al. 2007; Feitelson et al. 2004; Bockmuhl and Petersen 2002; Trosko 2006; Michor et al. 2004, 2005).
Variants of the Armitage-Doll model intended for prediction of radiation-induced cancer risk have been applied to data sets such as the Japanese atomic bomb survivors (Pierce and Mendelsohn 1999; Pierce and Vaeth 2003). The main finding is that the effect of relatively low acute radiation doses, such as those experienced by survivors of the Hiroshima and Nagasaki bombings, can be approximated based on the assumption that radiation effectively “accelerates” normal aging. In other words, a given dose of radiation is roughly equivalent to a certain amount of time with spontaneous mutation rates (Fig. 7). The excess cancer risk is described solely as a function of age and radiation dose, and variables such as age at exposure and time since exposure are not individually important. After irradiation, the ERR decreases approximately as the reciprocal of age. These conclusions are reasonably well supported by atomic bomb survivor data.
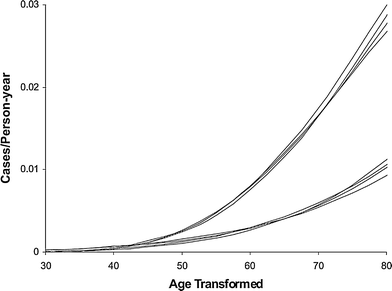

Fig. 7
Male and female age-specific cancer rates on transformed age scales, using the Pierce-Mendelsohn model (a derivative of the Armitage-Doll model), for the four dose categories of 0, 0.005, 0.5, and 1 Sv. The data are for non-sex-specific solid tumors in atomic bomb survivors. The four upper curves are for males, with age scale age + 4.1 dose, and lower curves are for females with age scale age + 6.4 dose. The figure and caption are reproduced from Pierce and Vaeth (2003)
3.2 Two-Stage Models with Clonal Expansion
The models in this class are based on the broad paradigm of initiation, promotion, transformation, and progression in carcinogenesis, which has been applied to numerous studies of chemically induced and radiation-induced tumors in experimental animals. They are also sometimes motivated by the concept of “two-hit” recessive oncogenesis, developed by Knudson to describe the data on sporadic and inherited forms of human retinoblastoma (Knudson 1971).
The most widely used representative of this class is the TSCE model (Moolgavkar 1978, 1980). It assumes that a stem cell which has acquired a single relevant mutation has a slight growth or survival advantage relative to normal cells (e.g., can proliferate at a faster rate and/or is more resistant to apoptotic signals). Over time, the growth advantage leads to clonal expansion of the mutated pre-malignant cell. When any cell within the clone acquires a second oncogenic mutation, it becomes a fully malignant cell, which can grow into a clinical cancer. Acquisition of the first mutation, leading from a normal to a pre-malignant cell, is called initiation. Clonal expansion of the pre-malignant cells is called promotion. Acquisition of the second mutation, leading from a pre-malignant to a malignant cell, is called transformation. Exogenous agents such as chemicals or ionizing radiation can affect these three processes, e.g., by initiating more normal cells and/or accelerating clonal expansion of the mutant ones. The general TSCE model assumptions are shown in Fig. 8.
As its name implies, the TSCE model therefore considers only two stages (i.e. initiation that makes pre-malignant cells and transformation that makes malignant cells) on the pathway to cancer. It focuses on tracking over time the number of once-mutated, initiated, pre-malignant cells. Usually this is done stochastically, i.e. an initiated cell can proliferate or die/differentiate or transform with certain probabilities per unit time. The clonal expansion rate is approximately the difference between the birth and death probabilities. Incidence of malignant cells is proportional to the number of initiated cells. A malignant cell gives rise to clinical cancer after a lag period, which is sometimes assumed to be constant (e.g., 10 years).
The TSCE model has been fitted to numerous data sets on spontaneous and carcinogen-induced tumors in animals and humans (Heidenreich et al. 1999, 2002, 2007; Heidenreich and Paretzke 2001). Spontaneous cancer incidence in humans over the age range of 20–70 is typically described very well, marginally better than by the previously discussed multistage models without clonal expansion, although the small differences in quality of fit are typically not statistically significant. The mechanistic implications are, however, different: In the models without clonal expansion, the “slope” of the spontaneous age-dependent cancer incidence curve is determined by the number of stages (mutations) on the pathway toward cancer. In the TSCE model, it is determined mainly by the net clonal expansion rate of initiated cells (i.e., by the difference between proliferation and death/differentiation rates for these cells). The typical cancer hazard function predicted by the TSCE model is shown in Fig. 9.
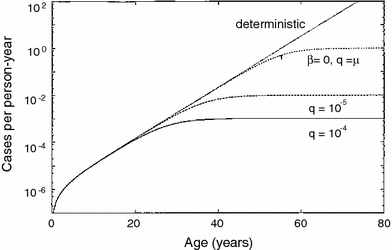

Fig. 9
The spontaneous cancer hazard function as function of age predicted by the TSCE model with various parameter values, from Heidenreich and Hoogenveen (2001). The deterministic version refers to the simplified case where clonal expansion is modeled deterministically, rather than stochastically, i.e., using only a net expansion rate instead of individual birth and death rates
The TSCE model has also been applied to radiogenic cancer risks in atomic bomb survivors, and many other radiation-related data sets. The fits have generally been good. The mechanistic interpretations of the observed patterns are, as for the spontaneous tumors, different from those using Armitage-Doll-type models: The radiogenic risk depends on age at exposure and time since exposure, and also on the degree to which radiation affects initiation versus promotion. If radiation affects predominantly (or exclusively) the initiation step, as is sometimes assumed, ERR decreases with age at exposure. If it affects predominantly promotion (i.e. accelerates the clonal expansion of already initiated cells), ERR is much less dependent on age at exposure. Predominance of initiation modulation is often inferred from analysis of atomic bomb survivors, although the possible role of promotion by low-LET photon radiation has recently drawn more attention (Heidenreich et al. 2007). Predominance of promotion modulation is usually inferred from analysis of long-term exposure to high-LET radiation, e.g., radon-exposed underground miners (Curtis et al. 2001).
The TSCE model explicitly addresses clonal expansion of pre-malignant cells, which has been observed or presumed in many organs, e.g., colon (Leedham and Wright 2008; Leedham et al. 2005; McDonald et al. 2006), liver (Kohle 2008; Rusyn et al. 2006), skin (Brash 2006; Brash et al. 2005), esophagus (Maley 2007; Maley and Reid 2005), bladder (Spiess and Czerniak 2006), and others (Perez-Ordonez et al. 2006), supporting the general conclusion that hyperplasia is a common property of pre-malignant cells. The ability of certain nongenotoxic substances (promoters) to produce cancers by inducing proliferation of already initiated cells also supports an important role for clonal expansion during carcinogenesis (Kohle 2008; Shaw and Jones 1994; Yamasaki 1992).
The TSCE model does not consider the possibly important effects of limitations of clonal expansion, e.g., due to tissue architecture (Michor et al. 2004; Leedham and Wright 2008; Leedham et al. 2005; Michor et al. 2003a; Calabrese et al. 2004; Komarova and Cheng 2006; Bennett et al. 2003; Potten and Booth 2002; Slack 2000) and diffusion-based size restrictions for pre-angiogenic tumors (Almog et al. 2006; Brem et al. 1977; Thomlinson and Gray 1955; Naumov et al. 2006; Hlatky et al. 1996). A recent TSL model (Sachs et al. 2005) attempts to include these factors.
3.3 Multistage Models with Genomic Instability
It is well known that cells in many tumors are genomically unstable. There are different types of genomic instability, such as chromosomal instability (CIN), which leads to loss or duplication of large pieces of chromosomes, and microsatellite instability (MIN), which leads to accumulation of more subtle DNA sequence changes. In either case, mutation rates throughout the genome can be elevated by several orders of magnitude above the normal values (Nowak et al. 2002, 2006). Presumably, this phenotype greatly accelerates the acquisition of mutations relevant for carcinogenesis, such as activation of oncogenes and loss of tumor suppressor genes. However, it remains unclear at what point, i.e., early or late, genomic instability usually appears during cancer development (Michor et al. 2003a, b; Nishimura et al. 2000; Finley et al. 2006). If it appears early, in the form of the so-called “mutator phenotype”, it may be a very important driving force for carcinogenesis because it accelerates subsequent mutation rates. If it appears late, by the time most of the mutational steps toward cancer have already occurred, it is probably less important, although destabilization of the genome even at a late stage may affect properties of the tumor such as resistance to therapy and acquisition of metastatic potential.
Many recent models of spontaneous carcinogenesis (Michor et al. 2004, 2005) focus on genomic instability. It has also been included in models of radiation-induced cancers (Little and Li 2007; Little and Wright 2003; Ohtaki and Niwa 2001). Typically, in such models genomic instability is added to a multistage framework that essentially represents an extension of the concepts used in both the stochastic TSCE model and the Armitage-Doll model. The number of stages is an adjustable parameter, as for the Armitage-Doll model. The cells in each stage, however, can clonally expand by a stochastic process of births and deaths, as in the TSCE model. At some point, genomic instability can be acquired, presumably by a random mutation in some genome-guardian gene(s) (e.g., genes responsible for DNA repair, cell cycle checkpoints, etc.). Once this occurs, the unstable cell clone can proceed more quickly to subsequent stages leading to malignancy.
Because they include several phenomena, i.e., multiple mutational stages, clonal expansion, and genomic instability, such models are very flexible and can involve a very large number of potentially adjustable parameters (e.g., number of stages, mutation, and clonal expansion rates for each stage with or without genomic instability). Consequently, it is not surprising that they can adequately fit the data on age-dependent spontaneous cancer incidence. However, the quality of fit is usually no better than (or sometimes marginally worse than) that for simpler models such as the TSCE model (Little and Li 2007). This occurs in part because the simpler models already fit the data very well, so further improvement will always be marginal and may not reach statistical significance. This phenomenon is illustrated in Fig. 10. A more detailed discussion of some conclusions that can be drawn from comparing the fits of different models to spontaneous cancer incidence curves is presented below, in Sect. 4.
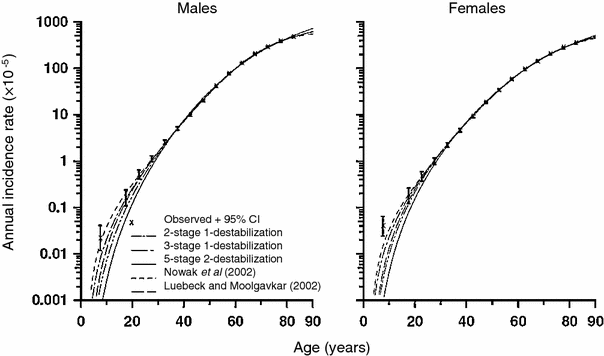

Fig. 10
Spontaneous colon cancer hazards predicted by models of Nowak et al. (2002) (with two cancer-stage mutations and one destabilizing mutation), of Luebeck and Moolgavkar (2002) (with four cancer-stage mutations and no destabilizing mutations), and of Little and Wright (2003) (with two cancer-stage mutations and one destabilizing mutation, three cancer-stage mutations and one destabilizing mutation, five cancer-stage mutations and two destabilizing mutations), with stem cell population fixed to 108 cells, fitted to SEER colon cancer data. The figure and caption are reproduced from Little and Li (2007)
Some inference about the potential role of genomic instability in radiation-induced cancers can be made using available data. One consequence of genomic instability is the prediction that cancer ERR should increase with time since exposure because the mutation rate(s) would remain elevated. This intuitive conclusion is supported by mathematical results (Little and Wright 2003). The data from atomic bomb survivors generally do not support this: in the long run ERR for most cancers remains constant or decreases with time since exposure. A plausible interpretation is that low-LET radiation may not induce genomic instability that persists long enough to substantially affect cancer incidence. This does not mean that genomic instability is unimportant in spontaneous incidence of the cancer in question—for example, instability could be already present before irradiation, and the exposure would have no substantial impact on this phenomenon. Also, an increase of ERR with time since exposure is suggested by some second cancer data sets, e.g., for colon cancer in radiotherapy-treated cervical cancer patients (Chaturvedi et al. 2007). Such findings may support the alternative interpretation that radiation-induced genomic instability may be important for carcinogenesis, at least for some tumor types.
3.4 Old Age Effects
As mentioned above, the incidence of typical adult-onset solid tumors rises quite steeply with age in the age range of 20–70. At older ages, however, the increase in incidence slows down and, for some cancers (e.g., breast, lung), is apparently reversed—incidence decreases for ages >80 (e.g. SEER database, http://seer.cancer.gov). Similar trends are seen in some animal cancer data sets (Pompei et al. 2001).
The reasons for these old age phenomena are not fully understood. For cancers of hormonally sensitive organs, such as the female breast, a decrease in incidence at old age may be due to large changes in hormonal status: e.g., clonal expansion of pre-malignant cells may slow down and many clones may become extinct when estrogenic stimulation is reduced. For cancers where population incidence is dominated by some exogenous risk factor, such as smoking in male lung cancer, cohort effects of different exposure to this factor may complicate true age effects: For example, individuals who are now in the oldest age groups may have, on average, smoked less during their lifetime than individuals in somewhat younger cohorts, producing an apparently lower cancer incidence at older ages. Variations in spontaneous carcinogenesis rates between individuals can also be important: If some individuals are more susceptible to getting cancer, e.g. because of some subtle defects in antineoplastic cell signaling or DNA repair capacity, they will get cancer at an earlier age. The oldest age groups will be depleted of these individuals, and enriched for those with lower cancer susceptibility (Fig. 11).
There may also be true physiological reasons for a turnover in cancer incidence at old age. A likely mechanism is senescence of stem cells and/or deterioration of stem cell function, or niche function, with age (Brunet and Rando 2007; Carlson and Conboy 2007; Sharpless and DePinho 2007). The number of viable normal stem cells may not necessarily decrease at old age, but their ability to proliferate may become impaired due to senescence of the stem cells themselves and/or loss of function of surrounding stem cell niche-forming cells (Fig. 12). Similar mechanisms may apply to some extent to mutated pre-malignant stem cells as well, leading to reduced carcinogenesis rates at old age.
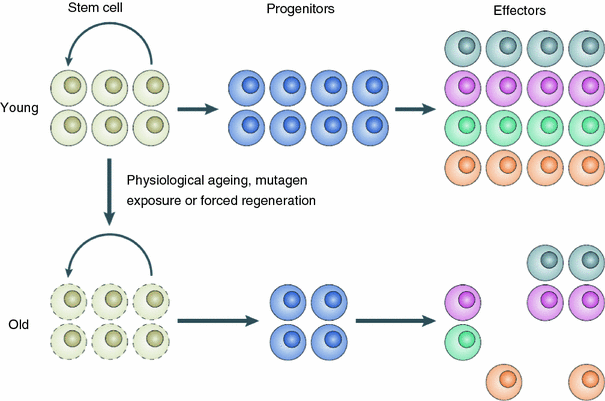

Fig. 12
A schematic representation of stem cell/stem cell niche aging, from Sharpless and DePinho (2007)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree