Fig. 14.1
Examples of TACs (time-activity curves) from several radiotracers
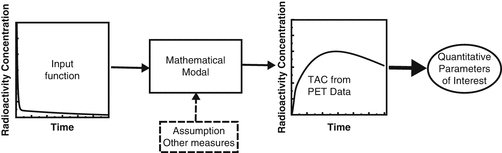
Fig. 14.2
Schematic diagram for analysis of tracer kinetics in PET data
14.3 Compartmental Model
This section describes compartmental model in mathematical point of view. Nomenclature and units in the text are tried to be consistent with recent consensus nomenclature [4].
14.3.1 Definition and Assumptions of a Compartmental Model
Figure 14.3 shows schematic drawings of three important compartmental models, namely, one-tissue compartmental model (1TC model), two-tissue compartmental model (2TC model), and three-tissue compartmental model (3TC model). As shown in this figure, several boxes are assumed to describe tracer’s behavior inside the living organism. Each box is called “compartment” and represents a pool of homogeneous tracer substance. A tracer is transferred between compartments with a first-order rate constant (K 1, k 2, k 3, k 4, k 5, k 6 in Fig. 14.3) which is proportional to the concentration of the tracer in the compartment. The “compartment” is fairly conceptual and could be a spatial region or a chemical state.
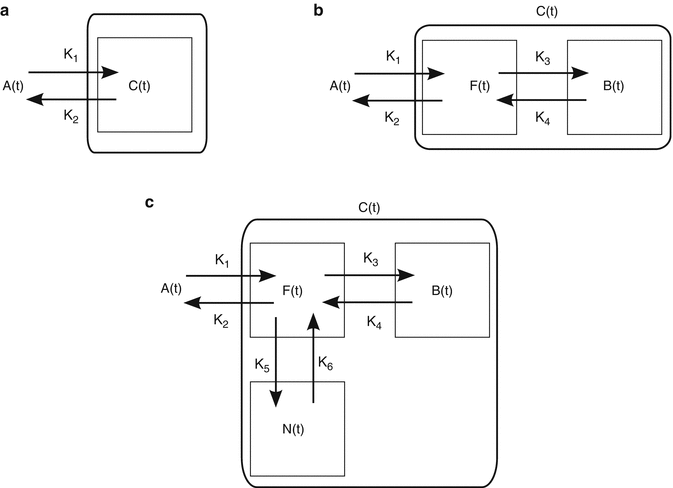

Fig. 14.3
Examples of compartmental models. (a) 1TC model, (b) 2TC model, and (c) 3TC model. A(t) input function, F(t) TAC in free (nondisplaceable) compartment, B(t) TAC in specific binding compartment, N(t) TAC in nonspecific binding compartment
A(t) [Bq/mL] in Fig. 14.3 is time course (a function of time t [min]) of radioactivity concentration of the tracer, which delivers the tracer in the system and is called input function. The input function A(t) is usually referred to the radioactivity concentration in blood or plasma and measured by frequent sampling of blood after administration of the radiotracer. The magnitude and shape of the input function are highly influenced by the manner of injection of the radiotracer. C(t) [Bq/mL] in Fig. 14.3 is time course (a function of time t [min]) of the radiotracer in tissue measured by PET. Even though there are several compartments in tissue such as 2TC model and 3TC model in Fig. 14.3, PET can only measure total radioactivity concentrations of multiple compartments. We could refer C(t) as a response of the system for the input function A(t) (Fig. 14.2). The pharmacokinetics of most PET tracer can be expressed by either 1TC, 2TC, or 3TC model. Before analyzing PET data, we must choose the most proper model for the tracer of interest. It will be discussed how we select the proper model in the following sections.
14.3.2 Solutions of Compartmental Models
14.3.2.1 1TC Model
In 1TC model (Fig. 14.3a), the following differential equation is written between A(t) [Bq/mL] and C(t) [Bq/mL]:
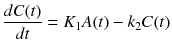
where rate constant from blood to tissue is K 1 [mL/cm3/min] and rate constant from tissue to blood is k 2 [1/min]. Note that K in K 1 is capitalized to distinguish other rate constants which have unit of [1/min]. K 1 is unit of volume of blood (or plasma) (mL) per volume of tissue (cm3) per minute. To solve differential equation with linear first-order parameters such as Eq. 14.1, Laplace transform can be utilized to solve the differential equation (Eq. 14.1) under the condition of C(0) = 0 as follows:
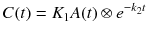
where e is exponential function and ⊗ represents the convolution operation and is equivalent to
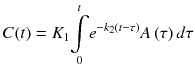
Figure 14.4a shows an example of generated C(t) from observed input function A(t) by 1TC model (Eq. 14.2 or 14.3) with K 1 = 0.5 [mL/cm3/min] and k 2 = 0.2 [1/min]. For intuitively interpreting convolution operation, the above equation can be written as
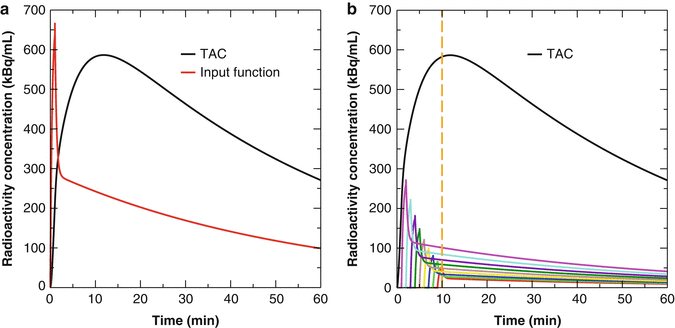
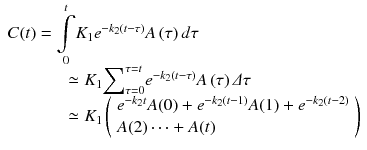
which indicates the C(t) at time t is influenced by A(t) in the past, i.e., A(0) and A(1) in Eq. 14.4. Figure 14.4b shows situation of Eq. 14.4 at time t = 10 [min]. It is also noticed K 1 is scaling the input function and determinant of the magnitude of C(t).
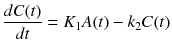
(14.1)
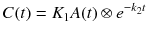
(14.2)
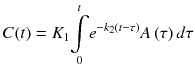
(14.3)

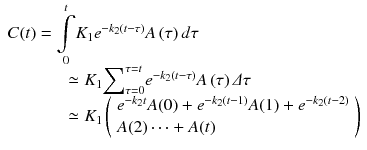
(14.4)
14.3.2.2 2TC Model
As shown in Fig. 14.3b, 2TC model has two compartments, and we often refer the first compartment as free compartment or nondisplaceable compartment (see detail in Sect. 14.4.2) and the second compartment as binding compartment, and their TACs are denoted F(t) [Bq/mL] and B(t) [Bq/mL], respectively. In 2TC model, two differential equations are derived with four parameters, K 1 [mL/cm3/min], k 2 [1/min], k 3 [1/min], and k 4 [1/min] as follows:
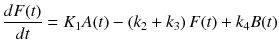
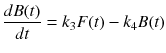
PET cannot distinguish between F(t) and B(t) and can only detect summation of two compartments C(t) expressed as
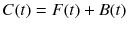
Using Laplace transform and combining Eqs. 14.5, 14.6, and 14.7, C(t) can be solved as follows:
![$$ \begin{array}{c}C(t)=\frac{K_1}{b_2-{b}_1}\Big[\left({k}_3+{k}_4-{b}_1\right){e}^{-{b}_1t}\\ {}+\left({b}_2-{k}_3-{k}_4\right){e}^{-{b}_2t}\Big]\otimes A(t)\end{array} $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ8.gif)
where β 1 and β 2 are defined as
![$$ {b}_{1,2}=\frac{1}{2}\left[\left({k}_2+{k}_3+{k}_4\right)\mp \sqrt{{\left({k}_2+{k}_3+{k}_4\right)}^2-4{k}_2{k}_4}\right] $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ9.gif)
There is a special case when k 4 is zero, which is often used for 18F-FDG, and we call it irreversible model because the tracer will be trapped in one compartment (see Fig. 14.7c) (in contrary, the tracer which is not trapped in the compartment is called reversible tracer). For the irreversible model, Eq. 14.8 becomes by setting k 4 = 0
![$$ C(t)=\frac{K_1}{k_2+{k}_3}\left[{k}_3+{k}_2{e}^{-\left({k}_2+{k}_3\right)t}\right]\otimes A(t) $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ10.gif)
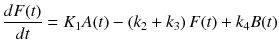
(14.5)
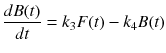
(14.6)
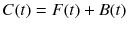
(14.7)
![$$ \begin{array}{c}C(t)=\frac{K_1}{b_2-{b}_1}\Big[\left({k}_3+{k}_4-{b}_1\right){e}^{-{b}_1t}\\ {}+\left({b}_2-{k}_3-{k}_4\right){e}^{-{b}_2t}\Big]\otimes A(t)\end{array} $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ8.gif)
(14.8)
![$$ {b}_{1,2}=\frac{1}{2}\left[\left({k}_2+{k}_3+{k}_4\right)\mp \sqrt{{\left({k}_2+{k}_3+{k}_4\right)}^2-4{k}_2{k}_4}\right] $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ9.gif)
(14.9)
![$$ C(t)=\frac{K_1}{k_2+{k}_3}\left[{k}_3+{k}_2{e}^{-\left({k}_2+{k}_3\right)t}\right]\otimes A(t) $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ10.gif)
(14.10)
14.3.2.3 3TC Model
As shown in Fig. 14.3c, 3TC model has three compartments in the tissue. TACs in the three compartments are often referred to as F(t) [Bq/mL] for free compartment, B(t) [Bq/mL] for specific binding compartment, and N(t) [Bq/mL] for nonspecific binding compartment. The following three differential equations are given:
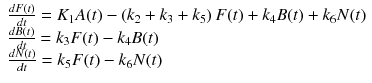
and the tissue TAC C(t) [Bq/mL] observed by PET is the summation of three compartments as follows:
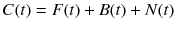
By using Laplace transform, the relationship between A(t) and C(t) can be expressed as
![$$ \begin{array}{l}C(t)={K}_1\left[{a}_1{e}^{-{b}_1t}+{a}_2{e}^{-{b}_2t}+{a}_3{e}^{-{b}_3t}\right]\\ {}\kern3.75em \otimes A(t)\end{array} $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ13.gif)
where β 1, β 2, and β 3 are three solutions of the cubic function below:
![$$ \begin{array}{l}{x}^3+\left({k}_2+{k}_3+{k}_4+{k}_5+{k}_6\right){x}^2\\ {}\kern1.5em +\left[{k}_4\left({k}_2+{k}_5+{k}_6\right)+{k}_6\left({k}_2+{k}_3\right)\right]x\\ {}\kern1.5em +{k}_2{k}_4{k}_6=0\end{array} $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ14.gif)
Several methods have been proposed for solving the cubic function, such as Cardano’s method. The α 1, α 2, and α 3 are defined as
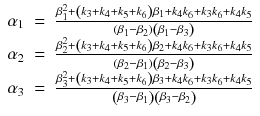
3TC model with six parameters can be theoretically solved; however, in practical, it is too complicated to apply 3TC model for the actual PET data that the reduction of parameters and some assumptions to constrain parameters are required [5].
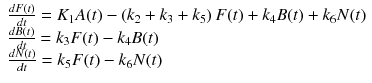
(14.11)
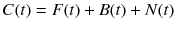
(14.12)
![$$ \begin{array}{l}C(t)={K}_1\left[{a}_1{e}^{-{b}_1t}+{a}_2{e}^{-{b}_2t}+{a}_3{e}^{-{b}_3t}\right]\\ {}\kern3.75em \otimes A(t)\end{array} $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ13.gif)
(14.13)
![$$ \begin{array}{l}{x}^3+\left({k}_2+{k}_3+{k}_4+{k}_5+{k}_6\right){x}^2\\ {}\kern1.5em +\left[{k}_4\left({k}_2+{k}_5+{k}_6\right)+{k}_6\left({k}_2+{k}_3\right)\right]x\\ {}\kern1.5em +{k}_2{k}_4{k}_6=0\end{array} $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ14.gif)
(14.14)
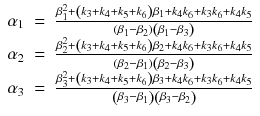
(14.15)
14.3.2.4 General Solution for Compartmental Model
Generally if there are n compartments in tissue, relationship between input function as A(t) and TAC as C(t) can be expressed as follows [6]:
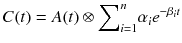
The input function A(t) is impulse or Dirac delta function, which is an infinite height at time 0 with an integral of one. If we define R(t) as follows
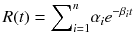
Equation 14.16 can be rewritten as
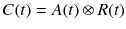
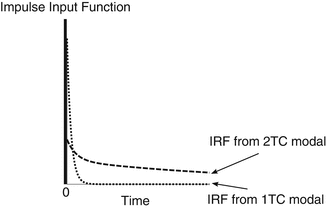
We call the function R(t) impulse response function (IRF) which is a system response against impulse input function. The α i and β i in R(t) are combinations of several rate constants as shown in Eqs. 14.8 and 14.9 for 2TC model and Eqs. 14.14 and 14.15 for 3TC model. IRF describes the behavior of the compartmental model which reflects properties of the injected tracer and the tissue of interest (see Fig. 14.5 for two examples of IRF). On the other hand, the shape of the input function is highly dependent on how the radiotracer is injected. As shown in Fig. 14.6, two input functions (Fig. 14.6a) produce very different TACs from a unique IRF. It is also worth to note that there are many possibilities of compartmental models to produce the same IRF. Figure 14.7a, c shows conventional 2TC models (one is reversible and the other is irreversible) and Fig. 14.7b, d models of two independent compartments inside. Their biological contexts are very different, but they share equivalent IRF in mathematical sense. The rate constants such as K 1, k 2, k 3, and k 4 are called micro-parameters and sometimes difficult to estimate with high precision due to noise in PET data, and only macro-parameters which are α i , β i , or combinations of α i and β i are available. For example, one of the most frequently used macro-parameters, total distribution volume V T [mL/cm3], is defined as below using Eq. 14.17 (see Sect. 14.4.2 for physiological definition of V T):
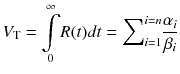
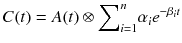
(14.16)
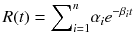
(14.17)
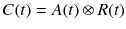
(14.18)

Fig. 14.5
Impulse input function and two response functions. Dotted line is generated from 1TC model and dashed line is generated from 2TC model

Fig. 14.6
(a) Two input functions, (b) IRF (dashed line), and two TACs generated from the two input functions (black and red lines)

Fig. 14.7
Examples of compartmental models which have two compartments in tissue. (a) Conventional 2TC model, (b) model with two independent compartments, (c) conventional irreversible model for 18F-FDG, and (d) model with two independent compartments: one is reversible and the other is irreversible compartment
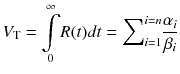
(14.19)
14.3.3 Parameter Estimation of Compartmental Model for PET Data
We will estimate rate constants or macro-parameters which explain the time course of the measured PET data. Generally, from input function A(t) and n data of TAC C PET(t i ) (i = 1, …, n) measured by PET, the parameters will be estimated by minimizing χ 2 in equation below:
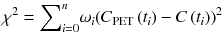
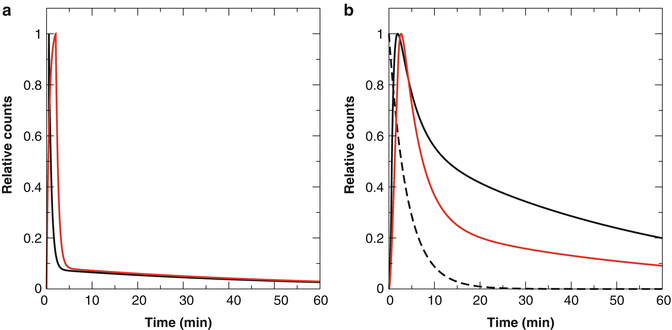
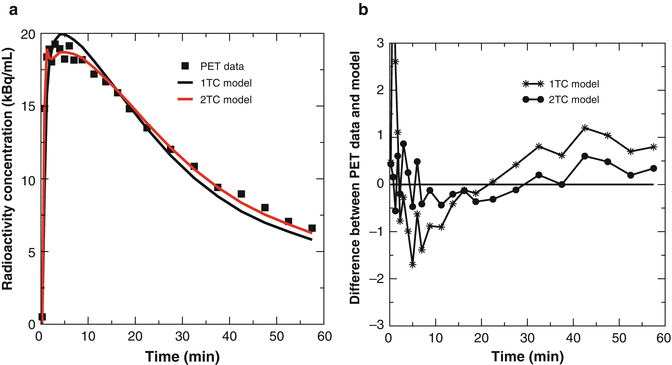
where C(t i ) is the estimated TAC at time t i calculated by Eq. 14.18 and ω i is the weighting factor at time t i and is inversely proportional to the variance of measured data C(t i ) (discussed below). Figure 14.8a shows examples of observed TAC and estimated TACs by 1TC model and 2TC model. Figure 14.8b shows plots of (C PET(t i ) − C(t i )). So the minimum χ 2 in Eq. 14.20 has the smallest offset from zero line in Fig. 14.8b.
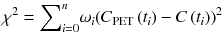
(14.20)

Fig. 14.8
Examples of fitting PET data by 1TC model or 2TC model. (a) Observed TAC data C PET(t i ) (filled square) and estimated TAC C(t i ) by 1TC model (black line) and 2TC model (red line). (b) Differences between C(t i ) and C PET(t i )
The problem to minimize χ 2 is called the weighted least squares problem. Especially, in the case of Eq. 14.18, ∂R/∂β i in Eq. 14.17 is not independent to β i , and we must deal with nonlinear least squares problem or nonlinear fitting problem. In general, to solve the nonlinear fitting problem, we must give the initial guesses of estimated parameters and iteratively calculate Eq. 14.20 until no further improvement is achieved. There are several techniques to update estimated parameters at each iteration. One major approach is to go to the steepest descent direction for each parameter by computing gradient of the parameter against Eq. 14.20. Another major approach known as the Gauss-Newton approach is to use the first-order Taylor series expansion which results in a linear function and can be solved by linear regression technique. The Marquardt-Levenberg algorithm is a composition of the steepest descent approach and Gauss-Newton approach [7]. The techniques mentioned above require calculation of derivatives, which sometimes introduces source of error since there is no analytic solution for the derivatives and numerical computation of derivatives must be carried out. Another approach, the downhill simplex method [8], requires no derivative calculation although the method itself is very slow.
The ω i in Eq. 14.20 must be set before the parameter estimation. The variance of PET data is related to many factors, including events of random coincidence and scattered photon inside the field of view (FOV), reconstruction algorithm, size of region, time duration of data acquisition, and time passed after the injection of radiotracer. Therefore, ω i must be set under assumption. The uniform weighting factor is often used, but this assumption must be used with caution especially for radiotracer with short half-lives such as 15O (about 2 min of half-life) and 11C (about 20 min of half-life), which have lower count rate at later time frames due to radioactive decay. By accounting for radioactive decay and frame duration, the weighting factor can be approximated as follows [9]:
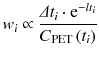
where Δt i [min] is the frame duration of PET data at time t i and λ is the decay constant (0.340 [min−1] for 15O, 0.0340 [min−1] for 11C, and 0.00631 [min−1] for 18F). Alternatively, the inverse of noise equivalent counts (NEC) as a good guess of variance in PET data is employed for approximation of ω i [10].
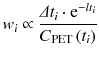
(14.21)
In contrast to the linear regression which has a unique solution without iterations, the nonlinear fitting does not guarantee to have one unique solution. Figure 14.9 shows schematic drawings to represent to search the solution in the nonlinear fitting. If the squared sum computed by given parameters looks like Fig. 14.9a, the solution is only one at the bottom of the valley. In the case of Fig. 14.9b, the sum of squares has many valleys (local minima), and estimated results are highly dependent on the starting point. In the case of Fig. 14.9c, there is only one valley of the squared sum, but many solutions are possible (Fig. 14.9).
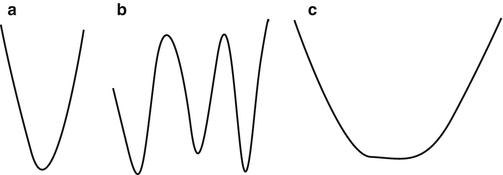
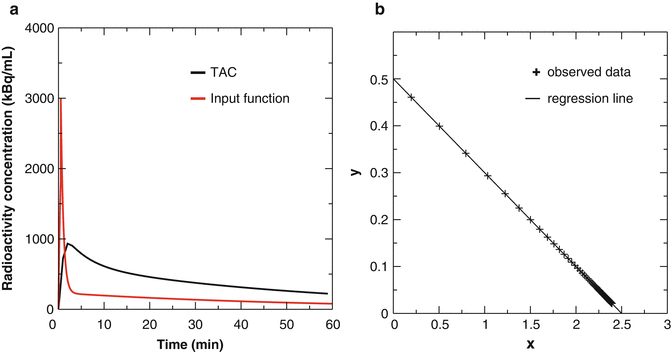

Fig. 14.9
Schematic drawings of solutions of nonlinear fitting. (a) Only one solution exists, (b) multiple local minima exist, and (c) many solutions are possible

Fig. 14.10
(a) TAC (black curve) and input function (red curve). TAC is generated by 1TC model with K 1 = 0.5[mL/cm3/min] and k 2 = 0.2[1/min]. (b) Plot of Eq. 14.24 and a regression line. Intercept of y-axis is 0.5[mL/cm3/min] as K 1 and x-axis is 2.5 as K 1/k 2
In Fig. 14.8a, b, it is apparent the 2TC model is better than the 1TC model for fitting the PET data. Generally a model with more parameters (four parameters for 2TC model versus two parameters for 1TC model) gives better fitting results. However, it is not always implying a model with more parameters can describe more precisely physiological or biological properties than simpler model. There are several statistical tests that have been proposed to compare between the models such as the AIC (Akaike information criterion), SC (Schwarz criterion, also called Bayesian information criterion (BIC)), or F-test [11]. Impulse response fraction [12] can be employed to predict the reliability of the model with more than one compartments over the 1TC model. The impulse response fraction for 2TC model is defined as
![$$ f=\frac{a_2\left[1-{\mathrm{e}}^{-{b}_2T}\right]/{b}_2}{a_1\left[1-{\mathrm{e}}^{-{b}_1T}\right]/{b}_1+{a}_2\left[1-{\mathrm{e}}^{-{b}_2T}\right]/{b}_2} $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ22.gif)
where α 1, α 2, β 1, and β 2 are from Eq. 14.16 under condition of β 1 < β 2 and T is the duration of data acquisition. This equation implies the relative contribution of the second compartment against the first compartment. If this fraction is close to 0, it is difficult to distinguish two compartments separately. It is also important to be aware of the identifiability of each micro-parameter. If the cross correlation between two parameters is high and these parameters are not independently identified, only macro-parameters must be utilized with confidence, or the simpler model is recommended to be used. It often happened that the 1TC model must be employed for analysis even though 2TC and 3TC models are a biochemically proper choice [5].
![$$ f=\frac{a_2\left[1-{\mathrm{e}}^{-{b}_2T}\right]/{b}_2}{a_1\left[1-{\mathrm{e}}^{-{b}_1T}\right]/{b}_1+{a}_2\left[1-{\mathrm{e}}^{-{b}_2T}\right]/{b}_2} $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ22.gif)
(14.22)
14.3.4 Linearization
As described above, nonlinear fitting to estimate parameters has several drawbacks including computational burden, large parameter variation, and poor parameter identification due to local minima. To overcome these problems, “linearization” techniques have been proposed, in which linear least fitting procedure is performed instead of the nonlinear fitting.
14.3.4.1 1TC Model
Equation of 1TC model is relatively easy to linearize due to simplicity of the model. Integration of Eq. 14.1 from time zero to time t yields
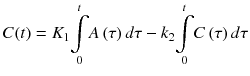
It is purposeful to use integration operation because PET scanner does not have enough temporal resolution to measure C(t) instantaneously, and the scanner actually measures the integration of C(t) over time. From the above equation, K 1 and k 2 can be solved by multiple linear regression technique between the dependent variable C(t) and two regressors,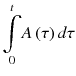 and
and 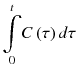 . Furthermore, dividingboth sides by
. Furthermore, dividingboth sides by 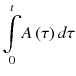 , Eq. 14.23 can be rewritten [13]:
, Eq. 14.23 can be rewritten [13]:
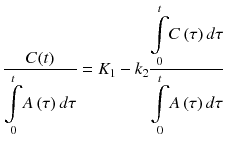
If we plot 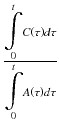 as x and
as x and 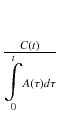 as y anda regression line is computed, intercepts of y-axis and x-axis are K 1 and V T = K 1/k 2, respectively.
as y anda regression line is computed, intercepts of y-axis and x-axis are K 1 and V T = K 1/k 2, respectively.
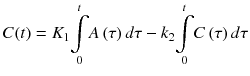
(14.23)
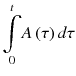 and
and 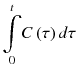 . Furthermore, dividingboth sides by
. Furthermore, dividingboth sides by 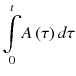 , Eq. 14.23 can be rewritten [13]:
, Eq. 14.23 can be rewritten [13]: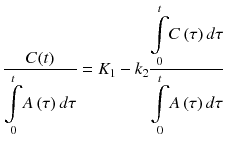
(14.24)
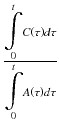 as x and
as x and 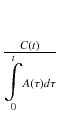 as y anda regression line is computed, intercepts of y-axis and x-axis are K 1 and V T = K 1/k 2, respectively.
as y anda regression line is computed, intercepts of y-axis and x-axis are K 1 and V T = K 1/k 2, respectively.Another popular linearization technique for 1TC model is an autoradiographic technique [14]. This technique is often used for measuring blood flow with 15O-H2O. Here, we assume the ratio of tissue concentration C to concentration of input function A at equilibrium is constant. p = C/A [mL/cm3] at equilibrium is called partition coefficient and p can be expressed as K 1/k 2 for 1TC model. If p is constant and known, integration of Eq. 14.2 from time t 1 to t 2 becomes
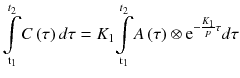
The right side of Eq. 14.25 is precomputed within reasonable range of K 1 using measured input function A(t) and fixed p value. By using thistable (look-up table) and measured 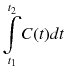 , K 1 is uniquely determined (Fig. 14.11).
, K 1 is uniquely determined (Fig. 14.11).
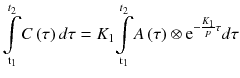
(14.25)
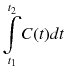 , K 1 is uniquely determined (Fig. 14.11).
, K 1 is uniquely determined (Fig. 14.11).
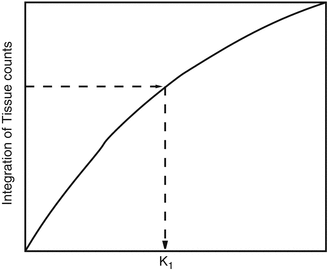
Fig. 14.11
Look-up table for autoradiographic technique.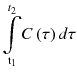 (y-axis) for different K 1 values areprecomputed, and from PET data, K 1 is uniquely determined
(y-axis) for different K 1 values areprecomputed, and from PET data, K 1 is uniquely determined
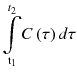 (y-axis) for different K 1 values areprecomputed, and from PET data, K 1 is uniquely determined
(y-axis) for different K 1 values areprecomputed, and from PET data, K 1 is uniquely determined14.3.4.2 Logan Plot
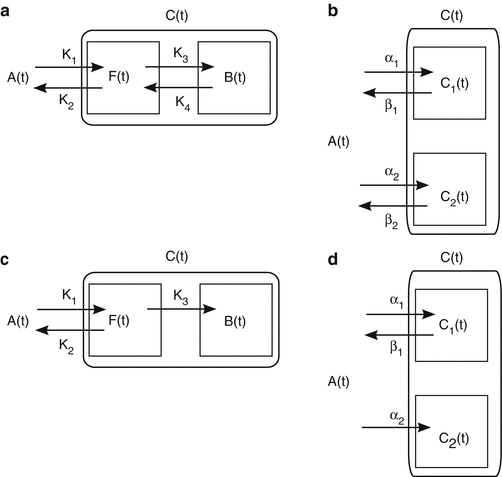
The most frequently employed linearization for reversible tracer is so-called Logan plot [15]. The Logan plot is a model-free approach since it does not require any assumption about the number of compartments. In this section, the formula of the Logan plot is derived from model with two independent compartments (Fig. 14.7b), but it is easily extendable for general model expressed in Eq. 14.16. For each compartment, the following differential equation can be written as similar as 1TC model:
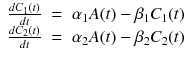
As same as Eq. 14.23, integration of both sides from 0 to time t yields
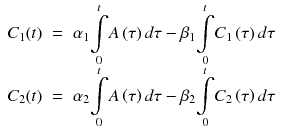
By arranging the above two equations and considering C(t) = C 1(t) + C 2(t), we will get the following equation:
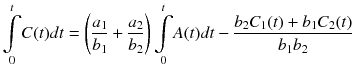
Both sides of the above equation is divided by C(t), and the equation becomes
![$$ \begin{array}{rcl}\frac{\underset{0}{\overset{t}{{\displaystyle \int }}}C\left(\tau \right)d\tau }{C(t)}& =& \left(\frac{\alpha_1}{\beta_1}+\frac{\alpha_2}{\beta_2}\right)\frac{\underset{0}{\overset{t}{{\displaystyle \int }}}A\left(\tau \right)d\tau }{C(t)}-\frac{\beta_2{C}_1(t)+{\beta}_1{C}_2(t)}{\beta_1{\beta}_2C(t)}\\ {}& =& {V}_{\mathrm{T}}\frac{\underset{0}{\overset{t}{{\displaystyle \int }}}A\left(\tau \right)d\tau }{C(t)}-\left[\frac{1}{\beta_1}+\frac{\beta_1-{\beta}_2}{\beta_1{\beta}_2}\frac{C_2(t)}{C(t)}\right]\end{array} $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ29.gif)
where V T is called the total distribution volume as defined by Eq. 14.19. If the Logan plot is theplot of 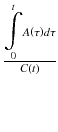 as x and
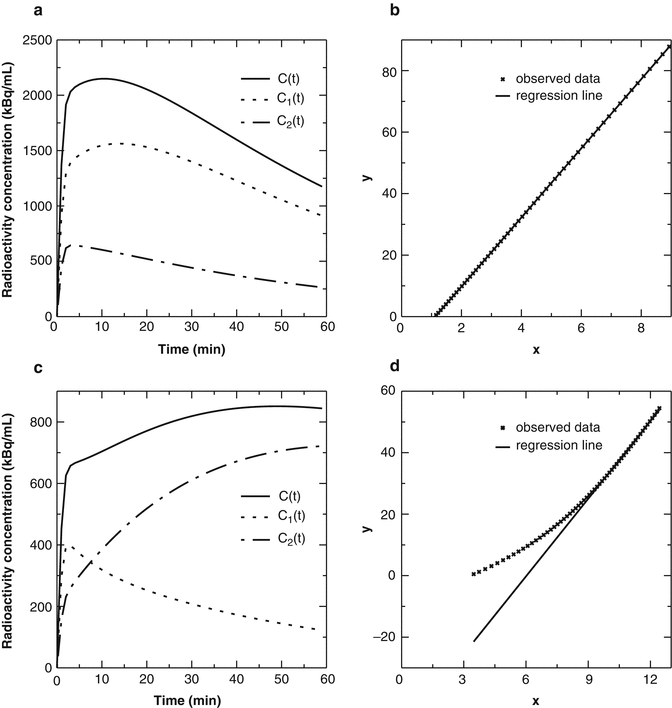
as x and 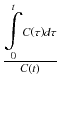 as y asshown in Fig. 14.12b), d, the plot is fitted well to straight line, and the slope of the line represents V T. Equation 14.29 indicates two particular cases dependent on the second term on the left side of the equation. If β 2 has a similar range to β 1 and is relatively large (fast kinetics Fig. 14.12a, b), C 2(t)/C(t) in the third term of Eq. 14.29 becomes constant. In this case, the Logan plot shows linearity from the beginning of the point (Fig. 14.12b). On the other hand, if β 2 is small and the tracer has slow kinetics (see TAC of C 2(t) in Fig. 14.12c), only later points of the Logan plot become linear as shown in Fig. 14.12d. The time beyond which the Logan plot becomes linear is called t*. The t* must be carefully determined. The wrong t* results in the underestimation of V T [16]. Another pitfall of the Logan plot is the problem of noise in the data [17]. The C(t) is in the denominators of both sides of Eq. 14.29, which introduces noise not only in the dependent variable (y) but also in the independent variable (x). To overcome these pitfalls, some attempts have been applied such as “multilinear analysis [16]” and “principle component analysis (PCA) [18].”
as y asshown in Fig. 14.12b), d, the plot is fitted well to straight line, and the slope of the line represents V T. Equation 14.29 indicates two particular cases dependent on the second term on the left side of the equation. If β 2 has a similar range to β 1 and is relatively large (fast kinetics Fig. 14.12a, b), C 2(t)/C(t) in the third term of Eq. 14.29 becomes constant. In this case, the Logan plot shows linearity from the beginning of the point (Fig. 14.12b). On the other hand, if β 2 is small and the tracer has slow kinetics (see TAC of C 2(t) in Fig. 14.12c), only later points of the Logan plot become linear as shown in Fig. 14.12d. The time beyond which the Logan plot becomes linear is called t*. The t* must be carefully determined. The wrong t* results in the underestimation of V T [16]. Another pitfall of the Logan plot is the problem of noise in the data [17]. The C(t) is in the denominators of both sides of Eq. 14.29, which introduces noise not only in the dependent variable (y) but also in the independent variable (x). To overcome these pitfalls, some attempts have been applied such as “multilinear analysis [16]” and “principle component analysis (PCA) [18].”
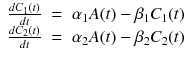
(14.26)
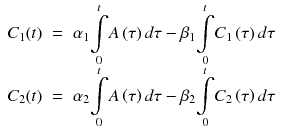
(14.27)
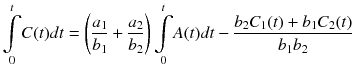
(14.28)
![$$ \begin{array}{rcl}\frac{\underset{0}{\overset{t}{{\displaystyle \int }}}C\left(\tau \right)d\tau }{C(t)}& =& \left(\frac{\alpha_1}{\beta_1}+\frac{\alpha_2}{\beta_2}\right)\frac{\underset{0}{\overset{t}{{\displaystyle \int }}}A\left(\tau \right)d\tau }{C(t)}-\frac{\beta_2{C}_1(t)+{\beta}_1{C}_2(t)}{\beta_1{\beta}_2C(t)}\\ {}& =& {V}_{\mathrm{T}}\frac{\underset{0}{\overset{t}{{\displaystyle \int }}}A\left(\tau \right)d\tau }{C(t)}-\left[\frac{1}{\beta_1}+\frac{\beta_1-{\beta}_2}{\beta_1{\beta}_2}\frac{C_2(t)}{C(t)}\right]\end{array} $$](https://radiologykey.com/wp-content/uploads/2017/10/A328756_1_En_14_Chapter_Equ29.gif)
(14.29)
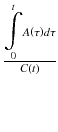 as x and
as x and 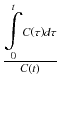 as y asshown in Fig. 14.12b), d, the plot is fitted well to straight line, and the slope of the line represents V T. Equation 14.29 indicates two particular cases dependent on the second term on the left side of the equation. If β 2 has a similar range to β 1 and is relatively large (fast kinetics Fig. 14.12a, b), C 2(t)/C(t) in the third term of Eq. 14.29 becomes constant. In this case, the Logan plot shows linearity from the beginning of the point (Fig. 14.12b). On the other hand, if β 2 is small and the tracer has slow kinetics (see TAC of C 2(t) in Fig. 14.12c), only later points of the Logan plot become linear as shown in Fig. 14.12d. The time beyond which the Logan plot becomes linear is called t*. The t* must be carefully determined. The wrong t* results in the underestimation of V T [16]. Another pitfall of the Logan plot is the problem of noise in the data [17]. The C(t) is in the denominators of both sides of Eq. 14.29, which introduces noise not only in the dependent variable (y) but also in the independent variable (x). To overcome these pitfalls, some attempts have been applied such as “multilinear analysis [16]” and “principle component analysis (PCA) [18].”
as y asshown in Fig. 14.12b), d, the plot is fitted well to straight line, and the slope of the line represents V T. Equation 14.29 indicates two particular cases dependent on the second term on the left side of the equation. If β 2 has a similar range to β 1 and is relatively large (fast kinetics Fig. 14.12a, b), C 2(t)/C(t) in the third term of Eq. 14.29 becomes constant. In this case, the Logan plot shows linearity from the beginning of the point (Fig. 14.12b). On the other hand, if β 2 is small and the tracer has slow kinetics (see TAC of C 2(t) in Fig. 14.12c), only later points of the Logan plot become linear as shown in Fig. 14.12d. The time beyond which the Logan plot becomes linear is called t*. The t* must be carefully determined. The wrong t* results in the underestimation of V T [16]. Another pitfall of the Logan plot is the problem of noise in the data [17]. The C(t) is in the denominators of both sides of Eq. 14.29, which introduces noise not only in the dependent variable (y) but also in the independent variable (x). To overcome these pitfalls, some attempts have been applied such as “multilinear analysis [16]” and “principle component analysis (PCA) [18].”