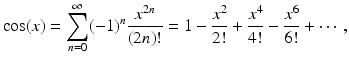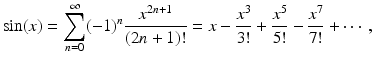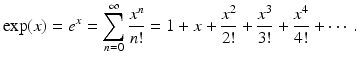(1)
Department of Mathematics and Statistics, Villanova University, Villanova, PA, USA
There is no real number a for which 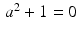 . In order to develop an expanded number system that includes solutions to this simple quadratic equation, we define the “imaginary number”
. In order to develop an expanded number system that includes solutions to this simple quadratic equation, we define the “imaginary number” 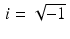 . That is, this new number i is defined by the condition that
. That is, this new number i is defined by the condition that 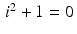 .
.
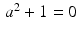 . In order to develop an expanded number system that includes solutions to this simple quadratic equation, we define the “imaginary number”
. In order to develop an expanded number system that includes solutions to this simple quadratic equation, we define the “imaginary number” 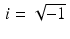 . That is, this new number i is defined by the condition that
. That is, this new number i is defined by the condition that 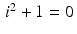 .
.Since 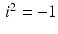 , it follows that
, it follows that 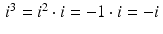 . Similarly,
. Similarly, 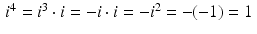 , and
, and 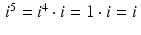 .
.
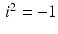 , it follows that
, it follows that 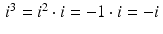 . Similarly,
. Similarly, 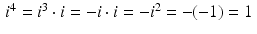 , and
, and 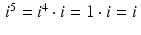 .
.As a quick observation, notice that the equation a 4 = 1 now has not only the familiar solutions a = ±1 but also two “imaginary” solutions a = ±i . Thus, there are four fourth roots of unity, namely, ± 1 and ± i . The inclusion of the number i in our number system provides us with new solutions to many simple equations.
4.1 The complex number system
The complex number system, denoted by ℂ, is defined to be the set
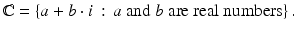 To carry out arithmetic operations in ℂ, use the usual rules of commutativity, associativity, and distributivity, along with the definition
To carry out arithmetic operations in ℂ, use the usual rules of commutativity, associativity, and distributivity, along with the definition 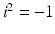 . Thus,
. Thus, 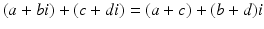 and
and 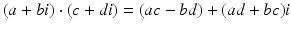 . Also,
. Also, 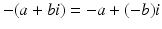 . Momentarily, we will look at division of one complex number by another.
. Momentarily, we will look at division of one complex number by another.
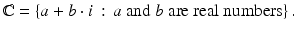
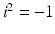 . Thus,
. Thus, 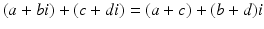 and
and 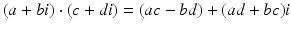 . Also,
. Also, 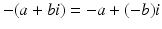 . Momentarily, we will look at division of one complex number by another.
. Momentarily, we will look at division of one complex number by another.A geometric view of ℂ . Each complex number 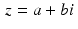 is determined by two real numbers. The number a is called the real part of z and is denoted by
is determined by two real numbers. The number a is called the real part of z and is denoted by 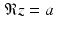 , while the number b is called the imaginary part and is denoted by
, while the number b is called the imaginary part and is denoted by 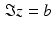 . (It is important to keep in mind that the imaginary part of a complex number is actually a real number, which is the coefficient of i in the complex number.) In this sense, the complex number system is “two-dimensional,” and so can be represented geometrically in the xy-plane, where we plot the real part of a complex number as the x-coordinate and the imaginary part of the complex number as the y-coordinate.
. (It is important to keep in mind that the imaginary part of a complex number is actually a real number, which is the coefficient of i in the complex number.) In this sense, the complex number system is “two-dimensional,” and so can be represented geometrically in the xy-plane, where we plot the real part of a complex number as the x-coordinate and the imaginary part of the complex number as the y-coordinate.
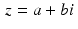 is determined by two real numbers. The number a is called the real part of z and is denoted by
is determined by two real numbers. The number a is called the real part of z and is denoted by 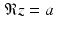 , while the number b is called the imaginary part and is denoted by
, while the number b is called the imaginary part and is denoted by 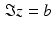 . (It is important to keep in mind that the imaginary part of a complex number is actually a real number, which is the coefficient of i in the complex number.) In this sense, the complex number system is “two-dimensional,” and so can be represented geometrically in the xy-plane, where we plot the real part of a complex number as the x-coordinate and the imaginary part of the complex number as the y-coordinate.
. (It is important to keep in mind that the imaginary part of a complex number is actually a real number, which is the coefficient of i in the complex number.) In this sense, the complex number system is “two-dimensional,” and so can be represented geometrically in the xy-plane, where we plot the real part of a complex number as the x-coordinate and the imaginary part of the complex number as the y-coordinate.A real number a can also be written as 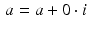 , and so corresponds to the point (a, 0) on the x-axis, which is known therefore as the real axis. Similarly, a purely imaginary number
, and so corresponds to the point (a, 0) on the x-axis, which is known therefore as the real axis. Similarly, a purely imaginary number 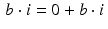 corresponds to the point (0, b) on the y-axis, which is called the imaginary axis.
corresponds to the point (0, b) on the y-axis, which is called the imaginary axis.
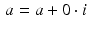 , and so corresponds to the point (a, 0) on the x-axis, which is known therefore as the real axis. Similarly, a purely imaginary number
, and so corresponds to the point (a, 0) on the x-axis, which is known therefore as the real axis. Similarly, a purely imaginary number 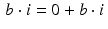 corresponds to the point (0, b) on the y-axis, which is called the imaginary axis.
corresponds to the point (0, b) on the y-axis, which is called the imaginary axis.The distance to the origin from the point (a, b) , corresponding to the complex number a + bi, is equal to 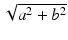 . Accordingly, we make the following definition.
. Accordingly, we make the following definition.
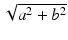 . Accordingly, we make the following definition.
. Accordingly, we make the following definition.Definition 4.1.
The modulus of the complex number a + bi, denoted by | a + bi | , is defined by
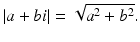
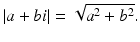
(4.1)
The modulus of a complex number is analogous to the absolute value of a real number. Indeed, for a real number 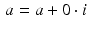 , we get that
, we get that 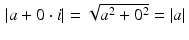 in the usual sense. Note also that
in the usual sense. Note also that 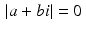 if, and only if,
if, and only if, 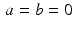 . A central observation is that
. A central observation is that
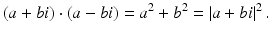 With this in mind, we make another definition.
With this in mind, we make another definition.
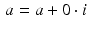 , we get that
, we get that 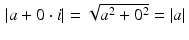 in the usual sense. Note also that
in the usual sense. Note also that 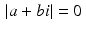 if, and only if,
if, and only if, 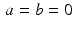 . A central observation is that
. A central observation is that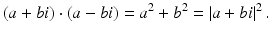
Definition 4.2.
The conjugate of a complex number a + bi , denoted by 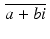 , is defined by
, is defined by
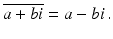
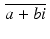 , is defined by
, is defined by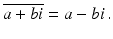
(4.2)
The central property, to repeat, is that
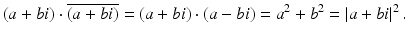
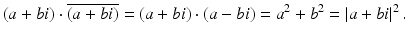
(4.3)
The conjugate of a complex number is the key ingredient when it comes to the arithmetic operation of division. For example, notice that
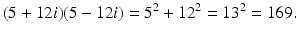 It follows from this that
It follows from this that
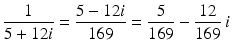 whence
whence
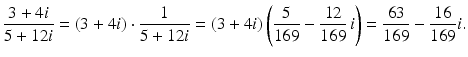
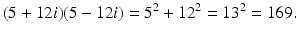
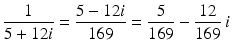
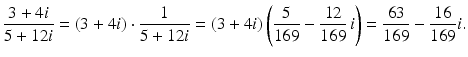
In general, we get that
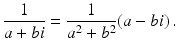 This enables us to divide any complex number by (a + bi) , provided that a and b are not both 0 . The act of dividing by the nonzero complex number (a + bi) is re-expressed as multiplication by (a − bi) and division by the nonzero real number (a 2 + b 2) .
This enables us to divide any complex number by (a + bi) , provided that a and b are not both 0 . The act of dividing by the nonzero complex number (a + bi) is re-expressed as multiplication by (a − bi) and division by the nonzero real number (a 2 + b 2) .
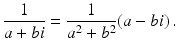
4.2 The complex exponential function
Consider these well-known Taylor series:
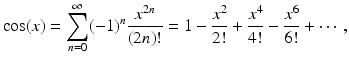
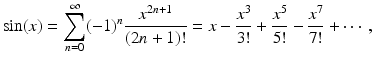 and
and