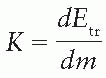9.3. PERCENTAGE DEPTH DOSE
One way of characterizing the central axis dose distribution is to normalize dose at depth with respect to dose at a reference depth. The quantity
percentage (or simply
percent)
depth dose may be defined as the quotient, expressed as a percentage, of the absorbed dose at any depth
d to the absorbed dose at a reference depth
d0, along the central axis of the beam (
Fig. 9.2). Percentage depth dose (
P) is thus
For orthovoltage (up to about 400 kVp) and lower-energy x-rays, the reference depth is usually the surface (
d0 = 0). For higher energies, the reference depth is usually taken at the position of
the
peak absorbed dose (
d0 =
dm) which occurs at greater depths, depending on energy. Since the depth of peak absorbed dose for a given energy beam also depends on field size (due to a varying amount of electron contamination incident on the surface), the reference depth,
d0, should be determined for a small field size (e.g., 3 × 3 cm
2) to minimize electron contamination and be kept the same for all field sizes irrespective of where the actual peak dose occurs.
In clinical practice, the peak absorbed dose on the central axis is sometimes called the maximum dose, the dose maximum, the given dose, or simply the Dmax. Thus,
A number of parameters affect the central axis depth dose distribution. These include beam quality or energy, depth, field size and shape, source to surface distance (SSD), and beam collimation. A discussion of these parameters will now be presented.
A. DEPENDENCE ON BEAM QUALITY AND DEPTH
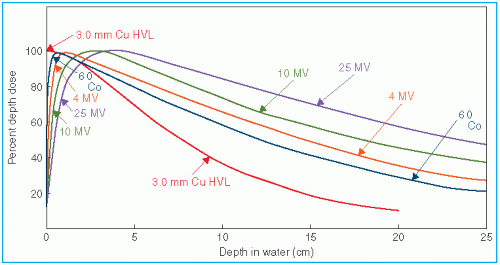
The percentage depth dose (beyond the depth of maximum dose) decreases with depth and increases with beam energy. Higher-energy beams have greater penetrating power and thus deliver a higher-percentage depth dose at a given depth (
Fig. 9.3). If the effects of inverse square law and scattering are not considered, the percentage depth dose variation with depth is governed approximately by exponential attenuation. Thus, the beam quality affects the percentage depth dose by
virtue of the average attenuation coefficient
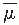
.
2 As the
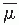
decreases, the beam becomes more penetrating, resulting in a higher-percentage depth dose at any given depth beyond the buildup region.
A.1. Initial Dose Buildup
As shown in
Figure 9.3, the percentage depth dose decreases with depth beyond the depth of maximum dose. However, there is an initial buildup of dose that becomes more and more pronounced as the energy is increased. In the case of the orthovoltage or lower-energy x-rays, the dose builds up to a maximum on or very close to the surface. But for higher-energy beams, the point of maximum dose lies deeper into the tissue or phantom. The region between the surface and the point of maximum dose is called the
dose buildup region.The dose buildup effect of the higher-energy beams gives rise to what is clinically known as the
skin-sparing effect. For megavoltage beams such as cobalt-60 and higher energies, the surface dose is much smaller than the
Dmax. This offers a distinct advantage over the lower-energy beams for which the
Dmax occurs at or very close to the skin surface. Thus, in the case of the higher-energy photon beams, higher doses can be delivered to deep-seated tumors without exceeding the tolerance of the skin. This, of course, is possible because of both the higher PDD at the tumor and the lower surface dose at the skin. This topic is discussed in greater detail in
Chapter 13.
The physics of dose buildup may be explained as follows: (a) As the high-energy photon beam enters the patient or the phantom, high-speed electrons are ejected from the surface and the subsequent layers. (b) These electrons deposit their energy until they are stopped, which occurs at a significant distance downstream from their site of origin. (c) Because of (a) and (b), the electron fluence and hence the absorbed dose increase with depth until they reach a maximum. However, the photon energy fluence continuously decreases with depth and, as a result, the production of electrons also decreases with depth. The net effect is that beyond a certain depth the dose eventually begins to decrease with depth.
It may be instructive to explain the buildup phenomenon in terms of absorbed dose and a quantity known as
kerma (acronym for “Kinetic Energy Released in the Medium” or “Kinetic Energy Released per Unit Mass”). As discussed in
Chapter 8, the kerma (
K) may be defined as “the quotient of
dEtr by
dm, where
dEtr is the sum of the initial kinetic energies of all the charged ionizing particles (electrons) liberated by uncharged ionizing particles (photons) in a material of mass
dm” (
14):
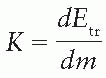
Because kerma represents the energy transferred from photons to directly ionizing electrons, the kerma is maximum at the surface and decreases with depth because of the decrease in the photon energy fluence (
Fig. 9.4). The absorbed dose, on the other hand, first increases with depth as the high-speed electrons ejected at various depths travel downstream. As a result, there is an electronic buildup with depth. However, as the dose depends on the electron fluence, it reaches a maximum at a depth approximately equal to the range of electrons in the medium. Beyond this depth, the dose decreases as kerma continues to decrease, resulting in a decrease in secondary electron production and hence a net decrease in electron fluence. As shown in
Figure 9.4, the
kerma curve is initially higher than the dose curve but falls below the dose curve beyond the buildup region. This effect is explained by the fact that the areas under the two curves taken to infinity must be the same.
B. EFFECT OF FIELD SIZE AND SHAPE
Field size may be specified either geometrically or dosimetrically. The
geometric field size is defined as “the projection, on a plane perpendicular to the beam axis, of the distal end of the collimator as seen from the front center of the source” (
15). This definition usually corresponds to the field defined by the light localizer, arranged as if a point source of light were located at the center of the front surface of the radiation source. The
dosimetric, or the
physical, field size is the distance intercepted by a given isodose curve (usually 50% isodose) on a plane perpendicular to the beam axis at a stated distance from the source.
Unless stated otherwise, the term field size in this book will denote geometric field size. In addition, the field size will be defined at a predetermined distance such as SSD or the source to axis distance (SAD). The latter term is the distance from the source to axis of gantry rotation known as the isocenter.
For a sufficiently small field one may assume that the depth dose at a point is primarily caused by the primary radiation, that is, the photons that have traversed the overlying medium without interacting. The contribution of the scattered photons to the depth dose in this case is negligibly small and may be assumed to be 0. But as the field size is increased, the contribution of the scattered photons to the absorbed dose increases since the volume that can scatter radiation gets larger with field size. Also this increase in scattered dose will be greater at greater depths.
The increase in PDD caused by increase in field size depends on beam quality. Since the scattering probability or scatter cross section decreases with increase in energy and the higher-energy photons are scattered more predominantly in the forward direction, the field size dependence of PDD is less pronounced for the higher-energy than for the lower-energy beams.
Percent depth dose data for radiation therapy beams are usually tabulated for square fields. Since the majority of the treatments encountered in clinical practice require rectangular or irregularly shaped (blocked) fields, a system of equating square fields to different field dimensions and shapes is required. Semiempirical methods have been developed to relate central axis depth dose data for square, rectangular, circular, and irregularly shaped fields. Although general methods (based on Clarkson’s principle—to be discussed later in this chapter) are available, simpler methods have been developed specifically for interrelating square, rectangular, and circular field data.
Day (
16) and others (
17,
18) have shown that, for central axis depth dose distribution, a rectangular field may be approximated by an equivalent square or by an equivalent circle. Data for equivalent squares, taken from the Hospital Physicists’ Association (
5), are given in
Table 9.2. As an example, consider a 10 × 20-cm field. From
Table 9.2, the equivalent square is 13.0 × 13.0 cm
2. Thus, the PDD data for a 13 × 13-cm field (obtained from standard tables) may be applied as an approximation to the given 10 × 20-cm field.
A simple rule-of-thumb method has been developed by Sterling et al. (
19) for equating rectangular and square fields. According to this rule, a rectangular field is equivalent to a square field if they have the same area/perimeter (
A/
P). For example, the 10 × 20-cm field has an
A/P of 3.33. The square field that has the same
A/P is 13.3 × 13.3 cm
2, a value very close to that given in
Table 9.2.
The following formulas are useful for quick calculation of the equivalent field parameter. For rectangular fields,
where a is field width and b is field length. For square fields, since a = b,
where
a is the side of the square. From
Equations 9.5 and
9.6, it is evident that the side of an equivalent square of a rectangular field is 4 ×
A/P. For example, a 10 × 15-cm field has an
A/P of 3.0. Its equivalent square is 12 × 12 cm
2. This agrees closely with the value of 11.9 given in
Table 9.2.
Although the concept of
A/P is not based on sound physical principles, it is widely used in clinical practice and has been extended as a field parameter to apply to other quantities such as backscatter factors (BSFs), TARs, and even beam output in air or in phantom. The reader may, however, be cautioned against an indiscriminate use of
A/P. For example, the
A/P parameter, as
such, does not apply to circular or irregularly shaped fields, although radii of equivalent circles may be obtained by the relationship






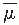 .2 As the
.2 As the 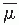 decreases, the beam becomes more penetrating, resulting in a higher-percentage depth dose at any given depth beyond the buildup region.
decreases, the beam becomes more penetrating, resulting in a higher-percentage depth dose at any given depth beyond the buildup region.