Dosimetry

where M _Q0 is the reading of the dosimeter at a reference condition and N _D,w,Q0 is the calibration coefficient in terms of absorbed dose to water for radiations of beam quality Q ₀ (normally ⁶⁰Co γ beam). In the radiation field having beam quality Q which is different from Q ₀, the absorbed dose can be obtained using the beam quality correction factor. That is, the dose at the standard depth of water can be obtained from the reading of the standard ionization chamber by

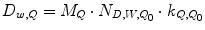
${D}_{w,Q}={M}_Q\cdot {N}_{D,W,{Q}_0}\cdot {k}_{Q,{Q}_0}$

where M _Qis the reading value of the standard dosimeter corrected for the influence quantities temperature and pressure, electrometer calibration, polarity effect, and ion recombination. In the case of scanned beams, the dose rate is very high and general recombination effects must be considered. k _Q,Q0 is a beam quality correction factor, which corrects the effect of difference between the reference beam quality Q ₀ and the actual user quality and can be obtained theoretically by the following formula:

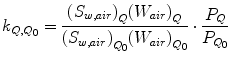
${k}_{Q,{Q}_0}=\frac{{\left({S}_{w, air}\right)}_Q{\left({W}_{air}\right)}_Q}{{\left({S}_{w, air}\right)}_{Q_0}{\left({W}_{air}\right)}_{Q_0}}\cdot \frac{P_Q}{P_{Q_0}}$

which includes the ratios at the qualitiesQ and Q ₀ of Spencer–Attix water/air stopping power ratios, S _w,air, of the mean energy expended in air per ion pair formed, W _air, and of the perturbation factors P _Q.

When Q ₀ is a ⁶⁰Co γ beam, it is recommended to use the following values:

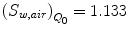
${\left({S}_{w, air}\right)}_{Q_0}=1.133$

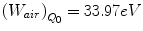
${\left({W}_{air}\right)}_{Q_0}=33.97 eV$

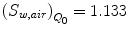
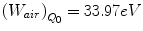
Since not much progress has been made in the investigation of the perturbation factor to be used for carbon beams, it is assumed to be 1.0. Therefore, in the case of carbon beams,

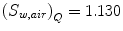
${\left({S}_{w, air}\right)}_Q=1.130$

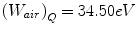
${\left({W}_{air}\right)}_Q=34.50 eV$

${P}_Q=1.0$

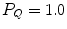
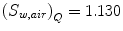
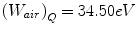
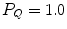
k _Q,Q0 values for carbon beam are dominated by the ratio of W _air values and the chamber-specific perturbation factors at ⁶⁰Co. The values for various cylindrical and plane-parallel ionization chambers in common use are tabled [1, 2].

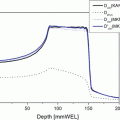
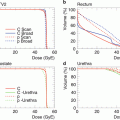
The following points should be noted regarding the ionization chamber to be used. Particle beams have Bragg peaks which change drastically throughout their depth–dose distributions. Therefore, when a depth–dose distribution is measured, a plane-parallel ionization chamber with high spatial resolution to the depth direction is often used. However, the plane-parallel ionization chamber has a greater uncertainty in P _wall than the cylindrical ionization chamber and has problems such as exhibiting a polarity effect and poor reproducibility. Thus the overall uncertainty of the plane-parallel ionization chamber is greater than that for the cylindrical type ionization chamber. Therefore, it is recommended to use the cylindrical type ionization chamber as the standard dosimeter for determining the absolute value of the absorbed dose to water. On the other hand, in the area near the Bragg peak, where the slope of the dose is large, it is appropriate to carry out measurements using the plane-parallel ionization chamber, which has a high spatial resolution. Therefore, it is recommended to calibrate the plane-parallel ionization chamber with the cylindrical type in the area where the dose distribution is flat and to use it for measuring the depth–dose distribution.

The following two cases are considered for standard conditions:

Case 1

A typical treatment beam having a spread-out Bragg peak (SOBP) is adopted as the standard condition. The reference point in this case is the center of the SOBP.

Case 2

The irradiation condition of the monochromatic energy is adopted as the standard condition. The reference point in this case is in an incident area where the dose distribution is flat.

Only gold members can continue reading. Log In or Register to continue