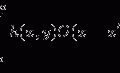Fig. 4.1
Schematic diagram of a scanning optical microscope. An EPSF in the focal plane is schematically illustrated. A sample includes a turbid medium and an object. Reprinted with permission from [1], 1999, Optical Society of America
It is clear that such an EPSF reflects not only the property of a microscopic imaging system but also the scattering property of a turbid medium. The parameters determining an imaging system include the numerical aperture (NA) of illumination and detection objectives and the size of the confocal pinhole v d. The parameters which describe a turbid medium are the scattering mean free path length l, the anisotropy value g, and the optical thickness n defined as the sample thickness divided by the scattering mean free path length l. According to the experimental conditions [12–15], we use an example scattering slab which has a thickness (d) of 180 mm and consists of polystyrene beads of diameter 0.48 μm suspended in water. The anisotropy value g of 0.48 μm beads is 0.81 for a He–Ne laser at wavelength 0.633 μm.
4.2 Two Dimensional Case
For a turbid medium of optical thickness n = 20, the EPSF as a function of the radial coordinate r = (x 2 + y 2)1/2 at the focus (z = 0) is shown in Fig. 4.2a for different sizes of the confocal pinhole. The EPSF has been normalized by its value at r = 0. Here we have assumed that the focal plane is placed in the middle of the turbid medium. If the focal plane is located at different depths of the turbid medium, the corresponding EPSF is different. It is noticed from Fig. 4.2a that the EPSF becomes narrower when a smaller confocal pinhole is used. The sharp component near r = 0 represents the contribution from ballistic photons . Statistically, multiple scattered photons are distributed further away from the center of the detector plane, and thus when a pinhole is used, these photons can be effectively rejected according to their deviation from the path that ballistic photons propagate. Therefore, using a pinhole of smaller size results in a narrower EPSF , which can lead to an image with higher resolution [11]. Figure 4.2b shows the EPSF for different values of the optical thickness n. As expected, the contribution from ballistic photons increases as the optical thickness becomes small.
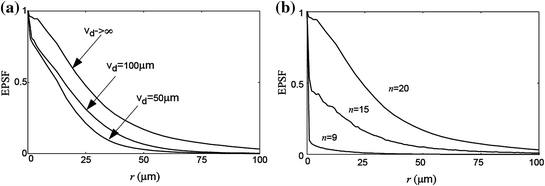

Fig. 4.2
Effective point spread function in the focal plane for a different sizes of the confocal pinhole, v d (NA = 0.25, n = 20) and b different values of the optical thickness n (NA = 0.25, v d = 100 μm). Reprinted with permission from [1], 1999, Optical Society of America
One may ask if the EPSF derived above satisfies a convolution operation , i.e., if the image intensity I(x, y) of a thin object can be modeled by the convolution of an object function O(x, y) and the EPSF h(x, y):
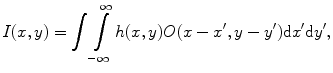
where h(x, y) is the EPSF in the focal plane. In order to demonstrate the validity of (4.1), and the efficiency and accuracy of the image modeling method in (4.1), we compare images modeled by the convolution algorithm in (4.1) with those modeled by the direct simulation method [12]. The object used for this comparison is a highly absorptive edge embedded in the middle of a turbid medium which has a thickness (d) of 180 μm and consists of polystyrene beads of diameter 0.48 μm suspended in water. This sample is scanned in the direction perpendicular to the edge. The illumination wavelength is assumed to be 0.633 μm. From the image intensity of the sharp absorption edge, the transverse resolution is defined as the distance between the 90 and 10 % intensity points.
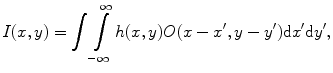
(4.1)
A comparison of the transverse resolution and computational time in the convolution method with those in the direct simulation method [12] is shown in Table 4.1. The computational time is recorded on a Pentium II 233 MHz PC for a given number of 5,000,000 incident photons for each image pixel. It can be seen from Table 4.1 that the difference in the resolution between the two methods is within 2–3 % for the optical thickness up to 20. This result confirms that the proposed EPSF satisfies the convolution relation in (4.1). The image modeling method which uses the convolution operation in (4.1) is much more efficient in saving computational time than the direct simulation method. For example, for an edge object (Table 4.1), the new method is approximately 15 times faster than the direct simulation time. The computational time in the convolution method mainly arises from the calculation of the EPSF . When the number of incident photons is increased, the computational time of the EPSF increases but the computational time of the convolution operation is not affected.
Table 4.1




Comparison of image resolution and computational time in the convolution method with those in the direct simulation method (Reprinted with permission from [1], 1999, Optical Society of America)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree