Flow-Compensated IVIM in the Ballistic Regime: Data Acquisition, Modeling, and Brain Applications
20.1 Introduction
20.1.1 The IVIM Imaging Concept
Intravoxel incoherent motion (IVIM) imaging has been used to obtain diffusion and perfusion information for more than three decades [1, 2]. As magnetic resonance imaging (MRI) hardware and acquisition techniques have improved over the years, the interest in IVIM imaging has increased and the number of applications has grown. The popularity of the method can partially be explained by the elegance in its simplicity; the diffusion MRI signal is modeled as a biexponential function of diffusion-encoding strength, where the two components correspond to the intravoxel signal contributions from diffusing spins and spins flowing through the microvascular network (perfusion):
(20.1)
The independent variable b is the diffusion encoding strength, S 0 is the signal without diffusion weighting, f is the so-called perfusion fraction, and the respective decay rates correspond to the diffusion coefficient in tissue (D t) and the pseudo-diffusion coefficient related to blood flow (D*). As such, the flow of blood through the microvascular network is modeled as a signal attenuation similar to a diffusion process, and diffusion and perfusion can be separated and quantified with appropriate data acquisition and analysis strategies. The water self-diffusion in blood, D b, may also be included, and the last term would then read fe -b(D b + D*).
In a majority of the IVIM research studies and applications, this original compact model has been employed and the data acquisition has usually been realized using a standard single diffusion encoding (SDE) MRI sequence, that is, the “Stejskal–Tanner sequence,” with varying diffusion encoding strengths. Furthermore, conventional IVIM analysis is based on biexponential least-squares fitting of diffusion-weighted signal data, a method that suffers from an inordinate sensitivity to noise. Although the pseudodiffusion coefficient of the flowing blood (D*) is approximately an order of magnitude larger than the regular diffusion coefficient, perfused capillaries contribute to the observable signal by only a small fraction (about 4% in the brain), and the IVIM effect is thus very difficult to detect with a high degree of reliability. Imaging and processing methods with a potential to improve the stability of the IVIM analysis would therefore be of considerable importance for the use of IVIM in clinical applications.
Some studies have indeed demonstrated the potential value in expanding the scope of the acquisition and modifying the IVIM model. In particular, the assumption that capillary blood particles flow mainly along straight paths during the encoding time allows for new imaging and processing approaches. This chapter aims to cover the underlying theory of the signal attenuation due to incoherent motion, the corresponding time dependence and temporal regimes, the effect of flow compensation, and examples of applications (primarily in the brain).
20.1.2 Temporal Regimes of Incoherent Motion
In 1907, Einstein noted that it would be “impossible” to measure the instantaneous velocity of a Brownian particle because the velocity and direction of the motion would be rapidly and randomly altered, even during an “extraordinarily short” observation time [3]. Although it took a little more than 100 years for Einstein’s statement to be challenged [3], we are still not even close to being able to measure ballistic Brownian motion with magnetic resonance techniques. On the other hand, random and pseudorandom particle motions with longer characteristic time scales of the velocity fluctuations, such as microvascular blood flow, can pertain to the “diffusive,” “ballistic,” or “intermediate” temporal regime and be probed with motion-/diffusion-encoded MRI [4]. The difference in scale between microscopic Brownian motion and macroscopic motion is enormous; the velocity fluctuations of a Brownian particle (such as a water molecule) at room temperature is of the order of ~10 ps, whereas macroscopic velocity changes of a blood water molecule traversing the human capillary network is believed to be of the order of ~100 ms. The latter time scale is of a similar order of magnitude as the motion encoding time (observation time) of the MRI sequence, which means that the temporal regime of microvascular blood flow is likely to depend on the settings of the pulse sequence protocol.
The characteristic time for velocity fluctuations (i.e., the average time for a particle to change speed and/or direction) can be defined by the velocity autocorrelation time T 0. If the motion encoding time of the MRI sequence is long compared to T 0, the blood particles change directions several times during the encoding, that is, mimic a diffusion process, and hence the motion is approximately diffusive (referred to as pseudodiffusion). It has been suggested that at least 6–10 velocity changes are needed for the diffusive approximation to be valid [4]. In the other limiting case, if the encoding time is short compared to T 0, the blood particles flow mostly along straight lines and this situation corresponds to the ballistic regime. Finally, if the encoding time is close to T 0, the motion pertains to the intermediate regime. It is of particular interest, in this context, to note that flow compensation affects the signal attenuation curves for motion patterns belonging to the intermediate and ballistic regimes and flow compensation can therefore be used to characterize and quantify microvascular blood flow and also to improve IVIM imaging. This chapter will mainly focus on the ballistic regime.
20.1.3 Motion Patterns in the Microvascular Network
Independently of the IVIM concept, Nalcioglu et al. and Ahn et al. developed an alternative method to estimate the relative capillary density [5, 6]. In the corresponding model, it is assumed that the blood flows coherently, on a subvoxel scale, in straight and randomly oriented capillary segments (i.e., the ballistic regime, as previously described). Coherent motion normally leads to a shift in the MR signal phase (see phase contrast MR), but variations in blood particle velocities and/or spatial orientation of capillary vessel segments yield a phase dispersion, resulting in a signal attenuation similar to that of pseudodiffusion. An important difference from diffusive motion is that the phase shift caused by straight flow in an individual segment can be rephased (i.e., the spin magnetization can be refocused) using velocity/flow compensation, and the corresponding signal attenuation caused by the collective effect of a large number of randomly oriented segments can thus be inhibited. Therefore, a combination of noncompensated (NC) and flow- compensated (FC) data was suggested as a way to probe perfusion [6]. In the original IVIM work by Le Bihan et al., it was acknowledged that both the pseudodiffusion model (i.e., the diffusive regime) and the straight-flow model (i.e., the ballistic regime) of microvascular blood flow would lead to much stronger signal attenuation than that of microscopic diffusion in tissue [2]. However, it was the pseudodiffusion interpretation and the corresponding model that primarily became associated with IVIM imaging.
Figure 20.1 displays a simplified illustration of the microvascular network in an MRI voxel, and the two limiting and contrasting cases, that is, diffusive and ballistic motion. As previously inferred, and elegantly described by Kennan et al. [4], the two models correspond to different temporal regimes (or extreme/limiting cases) of a more general description of a random walk, and the transition between them is referred to as the intermediate regime. To accurately describe and exploit random motion in the intermediate regime, even more delicate experiments and models are required, and this will be described in more detail in Chapter 21.
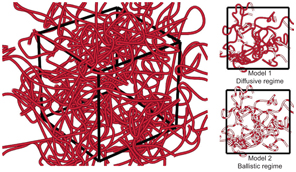
Figure 20.1 Schematic figure (not to scale) of the intricate network of highly tortuous and pseudorandomly oriented microvessels in a voxel (left). The two figures on the right visualize the two most common models for phase dispersion due to incoherent blood flow. In these figures, the red filling in the vessels corresponds to the pathway that a given blood particle has traveled during the motion encoding period. For the diffusive regime (Model 1), the blood particles travel relatively long distances and pass several bends of the capillaries. In contrast, for the ballistic regime (Model 2), the blood particles travel only a short distance and in mostly straight paths.
Since flow compensation, in theory, completely recalls the phase dispersion caused by velocity dispersion, Ahn et al. suggested calculating the signal difference between an FC and an NC acquisition, which would be proportional to the capillary density within the voxel (i.e., similar to the perfusion fraction f) [6]. Since then, a few other approaches of perfusion measurement using flow encoding have been proposed, as will be discussed in the following sections.
General flow and motion encoding with MR, that is, outside the field of perfusion MRI, has been described in detail in the past (e.g., Refs. [7–9]), and publications from these neighboring fields of MR are likely to serve as an important source of inspiration also in the future development of IVIM imaging.
20.2 Motion Encoding and Flow Compensation
20.2.1 General Signal Expressions
The normalized MR signal at echo time t E can be described as
(20.2)
where S 0 is the relaxation-weighted signal without motion encoding, f is the spin phase, and 〈⋅〉 denotes the ensemble average over the entire spin packet. The sensitivity of the signal to motion is adjusted by varying the magnetic field gradient G(t), that is, motion/diffusion encoding. The field gradient encodes the time-dependent spin position in the phase according to
(20.3)
where γ is the gyromagnetic ratio and x is the spin position. The cumulated phase at the echo time, caused by the combination of the motion encoding and the movement of spins, can also be described in terms of velocity, according to [9]
(20.4)
where v is the spin velocity. Summation over all subensembles according to Eq. 20.2 yields the normalized signal as [9]
(20.5)
where f(v) is the distribution of spin velocities. If the spin velocities are described by a Gaussian distribution, the phase distribution will also be Gaussian, and using Eq. 20.5, the normalized signal can be written as
(20.6)
where μ ϕ and
As shown below, at least one model discussed in this chapter is based on this approximation.
Using Eq. 20.4, it is possible to show that the phase shift of a spin or a spin packet with a constant velocity v c is given by
(20.7)
where α is the flow weighting factor. Later, velocity and orientation dispersion will be added for derivation of the corresponding signal equations. It can be shown that the flow weighting factor can be calculated in two ways, according to
(20.8)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree