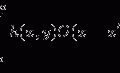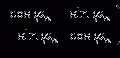Fig. 9.1
Images of a circular ring of inner radius 35 μm and outer radius 50 μm at different depths in the turbid medium: a d = 100 μm; b d = 150 μm; c d = 200 μm; d d = 250 μm. Reprinted with permission from [13], 2002, Elsevier
In this chapter, we use the expectation-maximization (EM) algorithm for maximum-likelihood (ML) image restoration [14]. The most basic form of the EM algorithm can be expressed as follows [14]:
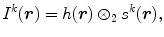
where I k (r) and s k (r) are, respectively, the image intensity and the estimated object function at kth iteration. The predicated image intensity I k (r) is compared with the recorded image intensity:
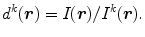
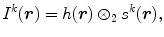
(9.1)
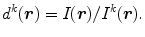
(9.2)
The ratio d k (r) is then projected back to the object space with a normalization factor H(0):
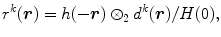
where r k (r) is a correction factor, and the normalization factor H(0) is derived as the two-dimensional integration of the EPSF. The estimated image intensity of the next iteration can be derived as:
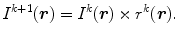
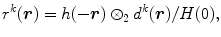
(9.3)
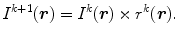
(9.4)
The deconvolved images after different numbers of iterations are shown in Fig. 9.2. Here we use the image at d = 200 μm depth as an example. Before the deconvolution process, the image is blurred and ring structure is totally washed out by the blurring effect. It is shown that the image resolution loss due to multiple scattering can be partially recovered through the image reconstruction process. After 200 iterations, the ring structure starts to re-emerge; however, the ring structure is still quite blurred. With more iterations, blurring on the ring structure becomes less significant. It is noted that the images after 1,000 and 2,000 iterations are very similar in terms of sharpness of the image, which indicates that the rate of convergence becomes significantly small and that the image will not be further improved through more iterations.


Fig. 9.2
Images of a circular ring: a before restoration; b after 200 iterations; c after 500 iterations; d after 1,000 iterations; e after 2,000 iterations. Reprinted with permission from [13], 2002, Elsevier
To further demonstrate the resolvability of the method, we designed an object which consists of two rings. Such an object emulates a biological cell cluster, and the deconvolution process of this object is demonstrated in Fig. 9.3. Before the restoration, the image at d = 200 μm is so blurred that not only the two rings cannot be resolved from each other, but also the individual structure of each ring cannot be identified. After 500 iterations, the two rings can be resolved from each other; however, the structure of each ring cannot be clearly identified. It is also noticed that the spherical symmetry of each ring is poor, which is a common defect occurring in the deconvolution process [15]. When the iteration number increases, the structure of each ring becomes clear and the spherical symmetry is also improved slightly. The comparison between Fig. 9.3d, e shows no significant improvement after 2,000 iterations , which means that numerical stability has been reached.
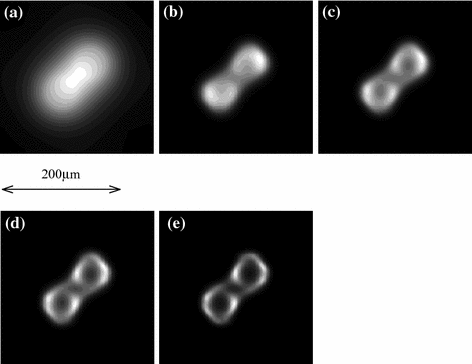

Fig. 9.3
Images of two circular rings: a before restoration; b after 500 iterations; c after 1,000 iterations; d after 2,000 iterations; e after 4,000 iterations. Reprinted with permission from [13], 2002, Elsevier
9.2 Noise Factor
We have demonstrated that with the accurate knowledge of the EPSF, image resolution can be improved significantly by mathematical restoration. However, there is another factor that has not been taken into consideration. Due to the highly scattering nature of tissue-like turbid media, the signal strength is usually weak in a thick sample, which results in poor signal-to-noise ratio . In order to demonstrate such an effect, a random noise is added to the image:
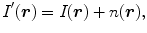
where n(r) is the noise function. In Figs. 9.4 and 9.5, the original images and the restored images of a single ring after 4,000 iterations with random noise of different magnitudes a are illustrated respectively. It is seen that the restored images become distorted if noise is included in the image; the poorer the signal-to-noise ratio, the more severely the image is distorted. Some artifacts also start to appear in the case of strong noise (Fig. 9.5d, e). Therefore, the noise in the image is the main obstacle in image restoration.

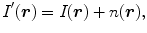
(9.5)

Fig. 9.4




Images of a circular ring of inner radius 35 μm and outer radius 50 μm with noise of different magnitudes a: a a = 0 %; b a = 10 %; c a = 20 %; d a = 30 %. Reprinted with permission from [13], 2002, Elsevier
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree