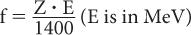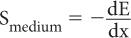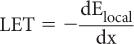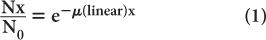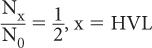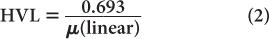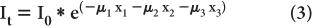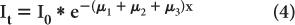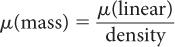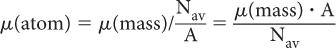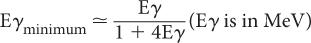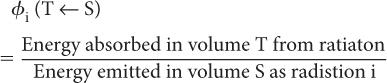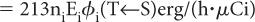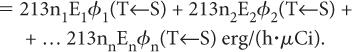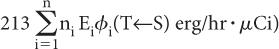In Vivo Radiation Detection: Basic Problems, Probes, and Rectilinear Scanners

Radiopharmeceuticals for Positron Emission Tomography (PET) Imaging

So far our discussion of radiopharmaceuticals has been limited to single photon imaging with a scintillation camera. Positron-emitting radionuclides, even though they emit particulate radiation and the γ-ray energy is high (511 KeV), are attractive from physiological reasons and may be the only radionuclides available to measure a particular physiological parameter. In this case, coincidence imaging discussed in Chapter 14 provides a better alternative to single photon imaging.

The ideal radionuclide for positron imaging is the one which does not emit γ-rays, emits positrons only with least amount of energy and is, hopefully, produced by a generator. In addition, it should provide clinically or physiologically important information that is not readily available with single photon imaging. Most of the radionuclides used in single photon imaging (^99mTc, ⁶⁷Ga, and ²⁰¹Tl) are not isotopes of physiologically important elements such as hydrogen, carbon, nitrogen, oxygen, or phosphorus. However, carbon, nitrogen, and oxygen each have only positron emitting isotopes (¹¹C, ¹³N, and ¹⁵O) that can be used for in vivo imaging. Unfortunately, their half-lives are in minutes only and none of these three is produced by a generator (Table 5.2). As a result, these have to be produced, labeled to a suitable physiologically interesting molecule, and imaged, depending on the radioisotope, within 10 minutes to an hour of the production. This puts tremendous hurdles in their routine clinical use, even when the cyclotron is at the site of usage. Therefore, their use so far has been limited to clinical research where they are providing a wealth of useful information.

However, another positron emitting radio-nuclide, ¹⁸F, (as fluoro-deoxy-glucose ¹⁸FDG, 110 minute half-life, see Chapter 2 for the decay scheme), despite it not being an isotope of a physiological important element, is increasingly finding more and more important clinical applications in nuclear medicine. This is in spite of the fact that it is not produced by a generator. Its half-life of about 2 hours (just long enough) and increasing demand make it feasible to produce ¹⁸F-labeled radiopharmaceuticals off site commercially and supply them to hospitals within a large metropolis at a reasonable price. Even though F is not a physiologically important element, it can be easily substituted for OH group in many physiologically important organic molecules such as glucose, without changing their function in a significant manner. As a result, it provides important information that is not easily available by other methods.

Luckily, several positron emitting radio-nuclides can be produced with a generator. Of these, two ⁶⁸Ga and ⁸²Rb are finding increasing use in nuclear medicine and their important physical properties are given in Table 5.2. The ⁶⁸Ge–⁶⁸Ga generator is now commercially available. A number of ⁶⁸Ga-labled compounds are under development. Of these, somatostatin analog, ⁶⁸Ga-Dotatoc (DOTA-DPhe1-Tyr 3-Octreotide) is very promising for the detection of a variety of tumors. Another generator is ⁸²Sr–⁸²Rb that produces ⁸²Rb with half-life of 1.3 minutes. This radionulide can be used for blood perfusion measurements, and studies can be repeated within few minutes if desired.

¹⁸FDG (2-deoxy-fluoro-D-glucose) ¹⁸FDG (2-deoxy-fluoro-d-glucose) is the work horse of PET imaging. Its applications range a wide gamut. It is used to diagnose a variety of brain diseases, measure regional brain function quantitatively, measure myocardial viability, and diagnose or stage a variety of cancers. Synthesis of ¹⁸FDG, as opposed to labeling with most of the other radiopharmaceuticals, is a complex procedure. However, most of these procedures have been optimized and are now highly efficient, fast, and automated. After the injection, ¹⁸FDG is quickly extracted from blood by tissues. The blood clearance is multiexponential, the fastest component having a half time of about 10 to 15 seconds, the next component having a half time of about 12 minutes. The third component is small and has a long half time. The target to blood ratio becomes optimum from 20 minutes post injection to 90 minutes post injection. As a consequence, most of the imaging is done between these times.

Like glucose, ¹⁸FDG is actively transported from blood through the cell membrane to the cytoplasm where, like glucose again, it goes through phosphorylation by the hexokinase reaction to ¹⁸FDG-6-phosphate. As opposed to glucose-6-phosphate, ¹⁸FDG-6-phosphate is not further metabolized in most tissues (liver, spleen, and kidneys are exceptions) and remains inside the cell for a long time. This is an advantage from the imaging point of view, as well as from quantification perspective, as it simplifies the number of compartments in which ¹⁸FDG is localized.

Radiopharmaceuticals in Pregnant or Lactating Women

It should be pointed out here that radiopharmaceuticals are, to various degrees, transferred to the fetus from mother through placental crossover and also excreted in motherís milk. Because these transfers are relatively minor as compared to overall distribution of the radiopharmaceutical in mother, this does not affect the imaging procedure. However, as discussed in Chapter 15, it poses potential risk to the fetus or baby if breast feeding. Chapter 7, p 77 discusses the radiation doses to the fetus from common radiopharmaceuticals and Chapter 16, p 178 provides ways to protect a breast feeding baby from potential radiation risk.

Therapeutic Uses of Radiopharmaceuticals

The main concern of nuclear medicine is diagnostic applications of radionuclides. Here, we briefly discuss some therapeutic uses of radiopharmaceuticals when they are administered internally to a patient.

Design of a Radiopharmaceutical for Therapeutic Uses Physiologic and biochemical considerations in designing a radiopharmaceutical for therapeutic purposes are similar to those that apply in designing a radiopharmaceutical for diagnostic uses; the primary objective in both cases is a high target to nontarget ratio. For therapeutic uses, a diseased cell is the target.

Because the objective of therapeutic use of a radiopharmaceutical is to kill diseased cells with radiation, the physical requirements for a radionuclide are the opposite of those desired for diagnostic purposes. The radionuclide should emit only particulate radiation (α– or β-ray) and preferably no penetrating radiation (x- or γ-ray). However, emission of x- or γ-ray in the range of 100 to 300 keV is not bad so long it does not contribute more than 10% to the total radiation dose. It can be used to image the distribution of the therapeutic dose in the patient to assess more accurately the radiation dose being delivered.

Problems and Uses The main problem arising in the treatment of a patient with internally administered radionuclides is the calculation of the radiation dose (gray or rad) to the target. Accurate calculations of the radiation dose require accurate data about the physical decay characteristics of the radionuclide and its distribution in the body (see Chapter 7). Although accurate data are available with regard to the first parameter, accurate data with regard to the latter are difficult to obtain, particularly in the case of a patient who is about to be treated. Usually, a tracer dose is administered to a patient for this purpose. From the blood disappearance, the urinary and fecal excretion rates, and the relative distribution in the body of this tracer dose, as determined by area imaging or SPECT where possible, estimation is made of the various parameters to be used in the calculation of the radiation dose. Unfortunately, even these parameters may not describe the behavior of the therapy dosage (100–1000 times larger than the trace dosage); therefore, the resulting radiation dose from a therapy dosage may be quite different from that estimated from the trace or diagnostic dosage. Another unpredictable factor in such treatment is the variability of the biological response of different individuals to the same radiation dose.

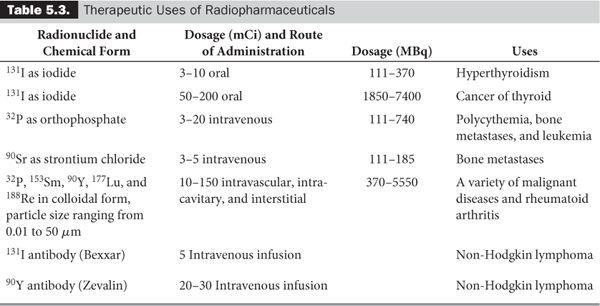
Despite this inability to deliver the exact number of grays (or rads) to a target by internal administration of the radionuclides, success has been achieved for the treatment of a number of diseases. Table 5.3 summarizes the present status of the therapeutic uses of internally administered radionuclides. Some of these radionulides are generator produced: ¹⁸⁸W – ¹⁸⁸Re and ⁹⁰Sr – ⁹⁰Y are two examples.

Misadministration of Radiopharmaceuticals

Radiopharmaceuticals, at rare occasions due to human error, can be administered in more amounts, in a different form, or through a different route than prescribed. In either case, the U.S. Nuclear Regulatory Commission (NRC) or comparable state agency, which regulates the use of FDA-approved radiopharmaceuticals and other uses of radionuclides, has defined what constitutes a misadministration. These are divided into three categories: the two radioisotopes, 125I and 131I, in the form of sodium iodide; all other diagnostic radio-pharmaceuticals; and all other therapeutic radiopharmaceuticals.

1. ¹²⁵I and ¹³¹I, in the form of sodium iodide: (a) Administration of a dosage greater than 1.1 MBq (30 μCi), or to a wrong patient, or through a wrong route and/or (b) whenever the administered dosage exceeds the prescribed dosage by more than 20% and the difference is greater than 1.1 MBq (30 μCi).

2. All other diagnostic radiopharmaceuticals: (a) Administration of a wrong radio-pharmaceutical, or to a wrong patient, or through a wrong route and/or (b) the radiation dose from the administered amount of radioactivity is more than 50 mSv (5 rems) effective dose equivalent or 500 mSv (50 rems) dose equivalent to any individual organ (radiation dose is described in Chapter 7).

3. All other therapeutic radiopharma ceuticals: (a) Administration of a wrong radio-pharmaceutical, or to a wrong patient, or through a wrong route and/or (b) when the dosage differs from the prescribed dosage by more than 20%.

After the discovery of misadministration, the NRC or appropriate state agency has to be notified no later than the next calendar day. Then a written report has to be submitted within 15 days providing the cause of misadministration and corrective actions taken and proposed.

These regulations are published in Title 10, part 35 of the Code of Federal Regulations (10CFR35) and should be consulted for more details.

Key Points

1. Radiation dose and the available detection instruments determine the characteristics of an ideal radionuclide to be used in nuclear medicine. An ideal radionuclide emits no particle radiation, emits an x- or γ-ray of energy in the range of 100 to 300 keV, and has a short half-life.

2. Pharmaceutical principles determine the localization of radiopharmaceuticals in tissues. These are active transport, compartmental localization, simple exchange or diffusion, phagocytosis, capillary blockade, cell sequestration, and receptor binding.

3. Radiopharmaceuticals have to satisfy quality control standards for radionuclidic purity, radiochemical purity, chemical purity, sterility, and apyrogenicity.

4. Commercial kits available for labeling with ^99mTc should be tested for two chemical impurities: ^99mTcO^–₄ and reduced or hydro-lyzed ^99mTc.

5. Labeling with ^99mTc dominates the radiopharmaceuticals used in nuclear medicine for diagnostic purposes.

6. Positron emitting radiopharmaceuticals such as ¹⁸FDG are also becoming routine in clinical nuclear medicine.

7. The radionuclide ¹³¹I dominates the therapeutic uses.

Questions

1. List the ideal properties of a radionuclide to be used for diagnostic purposes.

2. Three radionuclides with the following properties are available to you: (a) minutes, γ emission (70%) of 180 keV; (b) 1 day, γ emission (100%) of 250 keV, and a small fraction of conversion electrons (5%); (c) = 2 days, γ emission (20%) of 300 keV, β emission with a maximum energy of 2.0 MeV. Which one of these is best suited for (a) tumor localization when the optimum tumor uptake occurs at 18 hours post injection, (b) blood perfusion in an organ, and (c) radiation therapy?

3. List the factors that affect the localization of a radiopharmaceutical in tissue.

4. Does strong plasma binding of a radiopharmaceutical (a) help, (b) hinder, or (c) have no effect on the rate of uptake by a tissue?

5. What happens to the radionuclidic purity with time if the half-life of the desired radionuclide is longer than that of the radiocontaminant?

6. What are the two most common radiochemical impurities in a ^99mTc-labeled radiopharmaceutical?

7. How does the presence of oxygen interface with labeling of a pharmaceutical with ^99mTc?

8. List the various radiopharmaceuticals that are used for imaging the following organs: liver, bone, bone marrow, myocardium, blood pool, kidneys, lungs, hepatobiliary system, thyroid, spleen, tumors, and brain.

9. What is the main problem in routine use of the ¹¹C, ¹³N, and ¹⁵O radionuclides in nuclear medicine?

10. What is the optimum time for imaging with ¹⁸FDG?

11. Can positron emitting radionuclides be produced by a radionulide generator?

12. What are the ideal properties of a radionuclide to be used for therapy in nuclear medicine?

13. What are the main problems in the use of radionulides for therapy in nuclear medicine?

14. How do the roles of the two agencies, FDA and NRC, differ in regulating the radiopharmaceuticals?

15. What is the maximum time interval between the discovery of misadministration and its written notification to the appropriate agency?

Interaction is a fundamental aspect of nature. Our ability to see, hear, smell, and taste is a vivid manifestation of interaction. This chapter, however, focuses on the mechanism of interaction of high-energy radiation with matter. Radiation in this context is used in a general sense. It encompasses both corpuscular radiation (e.g., charged particles and neutrons) and electromagnetic radiation in the form of x- and γ-rays.

The material presented here is basic to an understanding of the detection and effects (especially biological) of high-energy radiation and of protection against it. Because the subject matter is complex, only the salient features are presented. For ease of presentation and understanding, this chapter has been divided into three sections: (1) interaction of charged particles (with energies of 10 keV to 10 MeV) such as e, e⁺, p, α, and ²D; (2) interaction of high-energy photons such as x- and γ-rays; and (3) interaction of neutrons.

Interaction of Charged Particles (10 keV to 10 MeV)

Principal Mechanism of Interaction When a charged particle passes through a substance (target) it interacts with the negatively charged electrons and positively charged nuclei of the target atoms or molecules. Through the coulomb forces, it tries to attract or repel the electrons or nuclei near its trajectory. As a result of these pushes and pulls (a sophisticated name for these is inelastic collisions), the charged particle loses some of its energy, which is taken up by the electrons of the target atoms near its trajectory. The absorption of energy by the target atom leads to its ionization or excitation. In this energy range (10 keV–10 MeV), ionization events predominate over excitation events. For this reason, high-energy radiations are sometimes referred to as ionizing radiations, although excitation events are by no means negligible. The probability of inelastic collisions in general is so high that it does not take a material of much thickness to stop the charged particles completely.

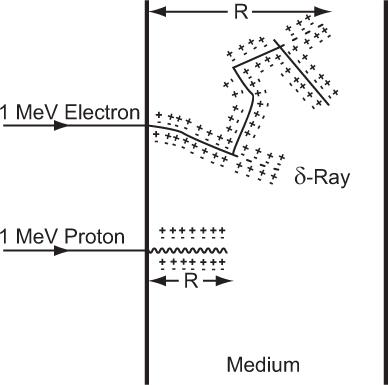
Differences Between Lighter and Heavier Charged Particles Do all charged particles interact in a similar way? The answer is yes and no. Yes, because inherently the nature of interaction for all charged particles in this energy range is the same (inelastic collisions). No, because the manifestation of these interactions on lighter particles—whose masses are of the order of an electron (e.g., e and e¹)—and heavier particles—whose masses are equal to or more than that of a proton (e.g., p and)—is strikingly different. Lighter particles in inelastic collisions with the electrons of the target atoms, besides losing energy, tend to be deflected at larger angles than the heavier particles. This leads to a wide variation in the paths of the two kinds of particles (depicted graphically in Figure 6.1 for an electron and proton). The path of a heavier particle is more or less a straight line, whereas that of a lighter particle is more tortuous (zigzag). Whenever a lighter charged particle is deflected at a large angle, the energy transferred to the target electron is also quite large. As a result, the target electron acquiring this large amount of energy also behaves like a high-energy charged particle, thus creating its own path in the target medium. The paths created by high-energy secondary electrons are known as δ-rays. These are shown by the dotted lines in Figure 6.1. In the case of a proton or other heavier particles, this type of energy transfer is rare.

Fig. 6.1. Range R of a charged particle. Heavy charged particles (e.g., protons) travel and lose their energy in more or less straight lines. Light charged particles (e.g., electrons) lose their energy in a zigzag fashion. Lighter charged particles can transfer large amounts of energy in a single encounter with an electron of the medium, thus creating what are known as δ-rays. Plus and minus signs represent the ionization of the atoms of the medium. (Figure not to the scale as electrons will travel much farther than protons.)

Range R of a Charged Particle As a charged particle travels farther and farther in a medium, it loses more and more energy and therefore more and more of the target atoms close to its path become ionized or excited. Eventually, the charged particle loses all its kinetic energy and comes almost to a halt. The average distance traveled by a charged particle in the incident direction is defined as its range R. This definition of range R is strictly valid only for heavy charged particles, such as particles. For lighter particles, it is difficult to define the range R exactly. For our purpose, it is sufficient to think of the range R of light particles such as electrons or positrons as the minimum thickness of a material that they are just unable to penetrate. The concept of the range of a charged particle is quite useful in radiation protection, design of radiation detectors, and radiation dosimetry.

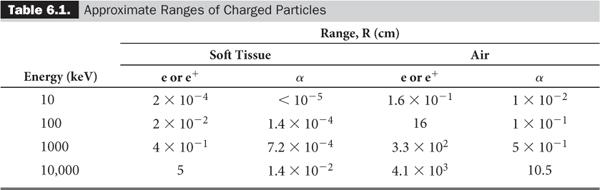
The range R of the heavier charged particles, because they travel more or less in straight lines, is nearly equal to the average path length of the charged particles in a given medium, whereas the range R for the lighter particles such as electrons, because of their more tortuous paths, is much shorter than the average path length (Fig. 6.1). Table 6.1 lists the ranges of α particles and electrons for various energies and mediums, providing a rough idea of the distances involved.

The concept of range is sometimes used with β-emitting radionuclides in which β particles are emitted with varying amounts of energy up to a maximum, Eβ_max. In this case, the range is more or less determined by Eβ_max.

Factors That Affect Range, R The range R of a charged particle depends on various factors. Four of the most important of these are described below.

Energy (E) The range R of a given particle increases with increase in the initial energy E of the particle. For example, the range of a 5-MeV electron is about six times longer than that of a 1-MeV electron. The exact relationship of R to E is complex, but in the energy range of our interest, R is linearly related to the initial energy of the charged particle E, or R = AE + B, where A and B are constants.

Mass (M) Lighter particles have longer ranges than heavier particles of the same energy and charge. The range of a 1-MeV positron (e⁺) is much longer than the range of a 1-MeV proton (p⁺, 2000 times the mass of an e⁺). Mass dependence of the range is sometimes expressed as velocity dependence. A 1-MeV positron is traveling at a much higher speed than a 1-MeV proton. The range R of a charged particle increases as the velocity of the charged particle increases.

Charge (Q) A particle with less charge travels farther than a particle with more charge. For example, a 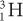(charge 1; mass 3) particle has a longer range than a 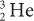(charge 2; mass 3) particle of the same energy. The exact relationship is R (1/Q²). Therefore, a 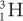particle travels four times the distance of 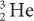particle. The signs of the charge (positive or negative) do not affect the range.

Density of the Medium (d) The range R of a charged particle strongly depends on the density of the medium through which it is traversing. The higher the density of the medium, the shorter the range of a charged particle; that is, R is inversely proportional to the density d of the medium or R α (1/d). For this reason, the ranges of charged particles are always much longer in gases than in liquids or solids.

Bremsstrahlung Production Besides losing energy through inelastic collisions, charged particles can lose energy through the “bremsstrahlung” process. In this case, when a charged particle in the electric field of a nucleus experiences a sudden acceleration or “de-acceleration,” it sometimes emits high-energy photons (x-rays). The probability of such interaction in the energy range of our interest is indeed very small except when electrons and positrons interact with high atomic-number materials (e.g., lead, steel). The fraction of energy f released as x-rays by electrons of energy E (MeV) in a material with atomic number Z is given approximately by the following equation:

In an x-ray tube with a tungsten target (Z = 74) and electrons with 100-keV incident energy, only 0.5% of the total energy of the electrons is converted into x-rays. The same fraction (0.5%) of the total energy of the electrons is converted into x-rays when a 1-MeV electron passes through water (Z = 7.4), except that the x-ray spectrum (energies of emitted x-rays) in this case is quite different from that produced in the first case (x-ray tube). For the purposes of nuclear medicine, because production of high-energy photons by this mechanism is generally very small, it is therefore ignored.

Stopping Power (S) Quite often, instead of using the range R of a charged particle, another parameter known as stopping power S is used. Stopping power is defined as the ratio of the amount of energy lost dE by a charged particle in traversing a small distance dx in a given medium to the distance dx, or

The range R is related to the stopping power in an approximately inverse relationship (i.e., the higher the stopping power of a given medium, the shorter will be the range of a given particle in that medium). Because of this relationship, the stopping power S also depends on the same factors (E, M, Q, and d) on which the range R depends, although the relationships are, approximately, inverse of the range R.

Linear Energy Transfer (LET) Linear energy transfer LET is an important parameter in radiation biology. It is defined as the ratio of the amount of energy transferred dElocal by a charged particle to the target atoms in the immediate vicinity of its path in traversing a small distance dx to the distance dx, or

Difference Between LET and Stopping Power S In discussing stopping power S one is concerned with the total energy lost by the particle, whereas in discussing LET one is concerned with the local (immediate vicinity of the track) deposition of energy by the charged particle. Because of this, S and LET are almost equal for heavier particles. For lighter particles, however, the two quantities differ significantly because of the energy lost in the δ-rays or through the bremsstrahlung process, which does not deposit energy locally. Both stopping power S and LET are measured in the same units (keV/μm).

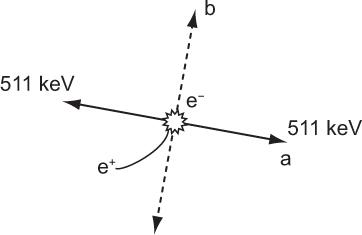
Annihilation of Positrons There is no difference in the way in which an electron or a positron loses energy in a medium. However, a positron, once it has lost its energy, is not stable and is quickly annihilated by combining with an electron. The mass energy of the electron and the positron is converted into two γ-rays of 511 keV that travel in opposite directions as shown in Figure 6.2. Remember that the annihilation of positron occurs only when it has lost almost all of its energy (i.e., near the end of its range in a medium).

Interaction of X- or γ-Rays (10 keV–10 MeV)

Although a photon does not have any electrical charge, it nevertheless interacts with electrical charges and therefore with matter that is composed of electric charges. The probability of interaction and the modes of interaction of a photon with matter are strongly dependent on the energy of the photon. Here we are interested only in the interaction of high-energy photons (x- or γ-rays) with matter.

The probability of interaction of an x-ray or γ-ray with an atom is, in general, very small compared with that of high-energy charged particles. As a consequence, x- or γ-rays have more penetrating power than high-energy charged particles. Because of this high penetrating power of x- or γ-rays, it is not practical to use concepts such as stopping power or range. Instead, new concepts known as linear attenuation coefficient (linear) and the half-value layer (HVL) are commonly used.

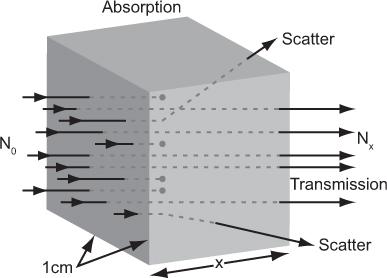
Attenuation and Transmission of X- or γ-Rays Let us consider a simple experiment in which a parallel beam of x- or γ-rays of a given energy E is incident on a thin slab of 1-cm² cross section and x-cm thickness (Fig. 6.3). When a γ-ray passes through this slab, three things may occur: the γ-ray may be completely absorbed by the material, the γ-ray may be deflected (scattered) with some or no loss of energy or the γ-ray may pass through the slab without any interaction. The first two processes together are known as attenuation; the third is known as transmission. The transmission of γ-rays of a given energy E_γ through a thickness x in the above experiment depends only on the nature of the material (density and atomic number) and the thickness x of the slab. For a given material, the dependence on the thickness x can be experimentally determined by measuring the number of γ-rays (those without any loss of energy or deflection) transmitted through different thicknesses of the slab. The data resulting from such an experiment can be accurately related by the following mathematical expression:

Fig. 6.2. Annihilation of a positron occurs when it loses almost all its energy at the end of its range and combines with an electron to produce two γ-rays of 511 keV. The two γ-rays are emitted always in opposite directions as shown in a or b or any other direction but always opposite to each other.

Fig. 6.3. Attenuation of γ-rays. When a flux N₀ of γ-rays is incident on a substance of x-cm thickness, a smaller flux N_x is transmitted by the substance (shown by the dots). The remaining γ-rays are either absorbed by the substance or scattered out from the incident beam.

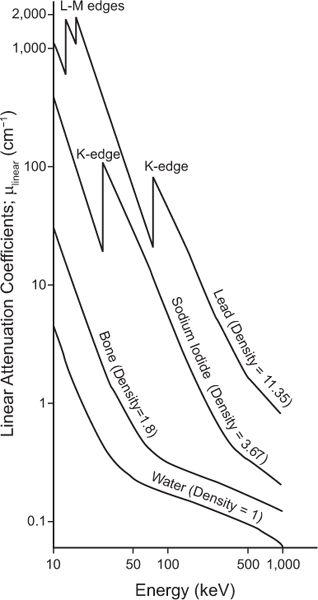
where N₀ and N_x are, respectively, the number of γ-rays incident on the slab and transmitted through a thickness x of the slab. The linear attenuation coefficient, μ(linear), represents in physical terms the probability of the interaction of a γ-ray passing through a unit area of a material 1-cm thick; γ(linear) strongly depends on the γ-ray energy E and the nature of the material (density and atomic number). Note that equation (1) is mathematically the same as that for radioactivity decay with time (see p. 23, Chapter 3). However, here it is describing a completely different physical process—namely, the transmission of γ-rays through a thickness x of a given material. The energy dependence of the linear attenuation coefficient of four substances useful for our purpose is shown in Figure 6.4.

Experimentally, it is easier to determine the parameter known as the HVL than to determine μ(linear). HVL is defined as the thickness of a material that attenuates one-half of the incident γ-rays. Referring to equation (1), when

HVL is related to (linear) by the following expression:

which is similar to that for the half-life of a radionuclide 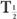and its decay constant. The parameter μ(linear) is measured in units of cm⁻¹, whereas HVL is expressed in cm. Once HVL or μ(linear) is known, one can easily determine the parallel beam attenuation of γ-rays through any thickness x of a material using equation (1) or one of the shortcuts described in Chapter 3 (p. 25) for solving problems involving exponentials.

Fig. 6.4. Linear attenuation coefficient (linear) of water, bone, sodium iodide, and lead as a function of x- or γ-ray energy.

Example:

The half-value layer of a 140-keV γ-ray in a NaI(Tl) crystal is approximately 0.3 cm. Determine the percentage of γ-rays transmitted through a 1.2-cm (≈ 1/2 inch) thick NaI(Tl) crystal for a 140-keV γ-ray parallel beam.

A thickness of 1.2 cm is expressed as 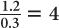HVL of a 140-keV γ-ray in a NaI(Tl) crystal. Because for 1 HVL the ratio 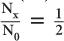, for 4 HVL the ratio will be 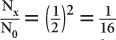; therefore, the percentage of γ-rays transmitted is 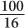or 6%. In other words, 94% of the γ-rays will be attenuated. Here, the thickness x is a multiple of HVL; therefore, it is not necessary to use equation (1).

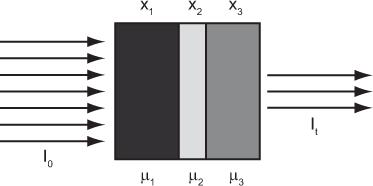
Attenuation Through Heterogeneous Medium Equation (1) describes the attenuation through a homogeneous medium only. When attenuation occurs through a heterogeneous material consisting of layers of different thickness of different materials as shown in (Fig. 6.5), then the attenuation is given by equation

where the total thickness, t = x₁ + x₂ + x₃

If x₁ = x₂ = x₃, then

In nuclear medicine, one encounters heterogeneous attenuation quite often. For example, during imaging of the heart, the γ-ray has to pass through different thicknesses of the heart muscle, lungs, and the bones. If not corrected, it introduces significant error in nuclear medicine images.

Mass Attenuation Coefficient, μ(mass) Because (linear) is dependent on the density of the absorbing material, it is often important to know the mass attenuation coefficient μ(mass) that removes the effect of the density from the linear attenuation coefficient. The mass attenuation coefficient reflects the probability of an interaction with a unit mass of a material. The mass attenuation coefficient is related to the linear attenuation coefficient by the following expression:

The units for μ(mass) are expressed as .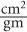

Fig. 6.5. Heterogeneous transmission through three layers of different tissues. Three different tissues with thicknesses of x₁, x₂, and x₃, and attenuation coefficients of μ₁, μ₂, and μ₃, respectively, make up the heterogeneous tissue. Total thickness of the tissue is t, and I₀ and I_t are the incident and transmitted flux of x- or γ-rays.

Atomic Attenuation Coefficient, μ(atom) The two probabilities of interaction, (linear) and (mass), describe the interaction of γ-rays at the macroscopic level (1 g or 1 cm³). How does one relate these two quantities to those at the atomic level (e.g., the probability of γ-ray interaction with one atom, μ[atom])? The number of atoms in 1 g of a substance can be determined by dividing Avogadro number N_av by the atomic weight A, that is, number of atoms in 1 g = N_av/A. Then (atom) can be determined by dividing μ(mass) by the number of atoms in 1 g of that substance:

The units for μ(atom) are expressed as cm².

Mechanisms of Interaction We described the attenuation of x- or γ-rays without, thus far, specifying the mechanisms that cause this attenuation. In this energy range (10 keV–10 MeV), there are three basic processes through which a photon interacts with matter: photoelectric effect, Compton scattering, and pair production. The relative importance of each type of interaction depends on the energy of the photon and the atomic number of the material with which it is interacting.

A salient feature of x- or γ-ray interaction with matter via any of the above three mechanisms is the production of a high-energy charged particle (electron or positron) that then loses energy in the medium by producing ionizations and excitations as previously discussed. Because of this, x- or γ-radiation is sometimes known as indirectly ionizing radiation.

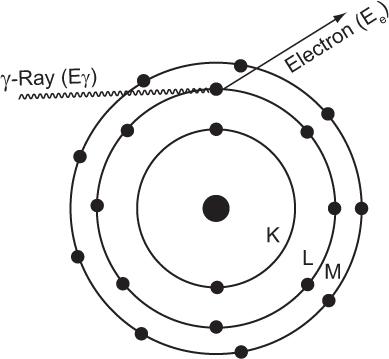
Photoelectric Effect When an incident photon interacts with a target atom through the photoelectric effect, it transfers all its energy to one of the electrons in the atom (i.e., the photon is completely absorbed by the atom), as shown in Figure 6.6. The absorption of energy by the atom leads to its ionization by the emission of an electron, which acquires kinetic energy Ee in an amount equal to that of the photon energy E minus the electron’s binding energy (BE) in the shell (; i.e., Ee = Eγ − BE of the electron). The electron can be released from any atomic shell. If it is released from one of the inner shells (e.g., K), a vacancy is created in this shell that is subsequently filled by an electron from one of the higher shells (e.g., L, M), as described in Chapters 1 and 2. This results in the emission of a characteristic x-ray or Auger electron by the atom. If, on the other hand, outer-shell electrons are involved in the photo-electric interaction, the atom is simply ionized. The probability of the photoelectric interaction by an atom τ(atom) strongly depends on two factors: the energy of the photon E and the atomic number Z of the atom involved in the interaction.

Fig. 6.6. Photoelectric interaction. A γ-ray transfers all its energy to an orbital electron of the absorbing material atom and thereby ionizes the atom. The electron thus released carries an amount of energy Ee that is equal to the γ-ray energy Eγ minus the binding energy of the electron in that orbit. If during ionization the vacancy is created in an inner orbit, a characteristic x-ray or Auger electron will also follow.

Dependence on Eγ The probability of photo-electric interaction (atom) decreases sharply with the increase in the x- or γ-ray energy. It is inversely proportional to the cube of γ-ray energy, that is, τ(atom) α(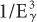). Therefore, the probability of a γ-ray of 45 keV interacting through the photoelectric effect is eight times higher than for a γ-ray of 90-keV energy, that is, (90³)/(45³) = 8. There is, however, one exception to this inverse cube law. Whenever the energy of the γ-ray Eγ becomes equal to the binding energies of the electrons in the various atomic shells of an atom, the probability of photoelectric interaction rises sharply. For example, the probability of the photoelectric interaction of a 45-keV γ-ray with a lead atom should be eight times higher than that of a 90-keV γ-ray according to the 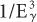rule. However, because the BE of the electrons in the K shell of a lead atom is about 88 keV, the probability of a photoelectric interaction of a 90-keV γ-ray increases to a point where it almost becomes equal to that for a 45-keV γ-ray. The probability of a photoelectric interaction of an 80-keV γ-ray in lead is about six times lower than that of a 90-keV γ-ray, despite the fact that the latter is a higher energy γ-ray. The regions where the 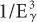law does not hold are called absorption edges, and their occurrence depends on the atomic number Z of the atom with which the γ-ray interacts. For example, the K absorption edge (where K-shell electrons are involved) occurs at approximately 88 keV in lead but at only 32 keV in iodine (Fig. 6.4).

Dependence on Z The photoelectric probability of interaction (atom) also depends strongly on the atomic number of the atom. It is directly proportional to the fourth power of the atomic number; that is, (atom) Z⁴. For example, the probability of γ-ray of a 50-keV interaction with a lead atom (Z = 82) is 11,000 times higher than that with an oxygen atom (Z = 8) because [82⁴]/[8⁴] = 11,000. Of course, if the γ-ray energy happens to be near one of the absorption edges of that atom, this rule is modified.

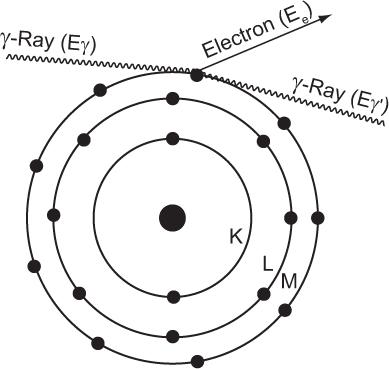
Compton Scattering In this process, a high-energy photon is scattered in billiard-ball fashion by an electron, as shown in Figure 6.7. The scattered electron gains energy and the incident photon loses energy. The exact amount of the energy gained by the electron or lost by the photon depends on the angle of scatter and the energy of the incident photon Eγ. In general, though, the larger the angle of scatter for a photon, the more energy it loses to an electron. Thus, the maximum transfer of energy from the photon to the electron occurs when the photon is scattered at an angle of 180 degrees (i.e., backscattered). The energy of the back-scattered photon (minimum energy of scattered photon) is related to the energy of the incident photon E by the following expression:

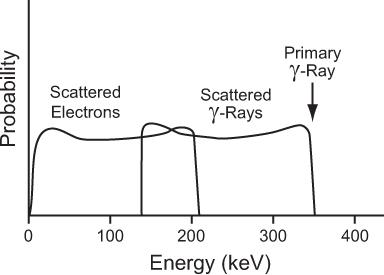
Fig. 6.7. Compton interaction. A γ-ray transfers only a partial amount of its energy to an orbital electron (usually the outer shell). The scattered γ-rays carry an energy Eγ’ that is equal to Eγ − Ee, where Eγ is the energy of the primary γ-ray and Ee is the energy carried by the scattered electron.

For a 1-MeV incident photon, the minimum energy of the scattered photon is 0.200 MeV; for a 0.360-MeV photon, 0.148 MeV; for a 0.140-MeV photon, 0.090 MeV; and for a 0.080-MeV photon, 0.060 MeV. These values of Eγ_minimum are given here as an illustration because of their relevance in γ-ray energy analysis by NaI(Tl) detectors (see Chapter 8). The energies of the scattered photons range from this minimum to that of the incidence photon energy. In Figure 6.8 we show the energy distribution of the scattered photons and scattered electrons for a 360-keV primary photon as a result of Compton interaction.

Dependence on E The probability of Compton interaction (atom) initially decreases slowly with the increase in energy E and then falls off more rapidly.

Dependence on Z Because each atom contains Z number of electrons, the probability of Compton interaction by an atom, σ(atom), is directly proportional to the atomic number, that is, σ(atom) α Z.

Fig. 6.8. Energy distribution of the scattered γ-rays and the scattered electrons in a Compton interaction of a 364-keV γ-ray. The maximum amount of energy that a 364-keV γ-ray can transfer to an electron via this process is 210 keV.

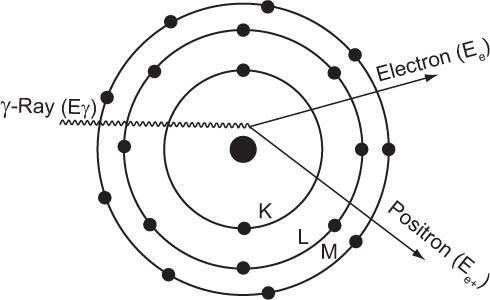
Pair Production For this interaction to occur, the energy of the γ-ray must be greater than 1.02 MeV. When a γ-ray of energy greater than 1.02 MeV passes through the electric field of a nucleus, it creates an electron and a positron (i.e., part of the γ-ray energy is converted into mass). This process is called pair production and is depicted in Figure 6.9. The excess energy of the γ-ray (Eγ − 1.02 MeV) is shared by e⁻ and e+ as kinetic energy.

Dependence on E The probability of pair production κ (atom) is zero below 1.02 MeV. At energies higher than 1.02 MeV, κ (atom) increases with increases in E and in fact becomes the dominant mode of interaction above 10 MeV.

Dependence on Z The probability of pair production (atom) for a given atom varies directly as Z².

Dependence of μ(mass) and μ(linear) on Z So far we have discussed the dependence of μ(atom) on Z for different processes of interaction. How do the linear and mass attenuation coefficients vary with atomic number? The linear attenuation coefficient μ(linear) and the mass attenuation coefficient μ(mass) depend on Z as Z³, Z⁰(i.e., no dependence on Z), and Z for photoelectric, Compton, and pair production modes of interaction, respectively. In this respect, it is important to remember that when the Compton scattering is the dominant mode of interaction, then each gram of any material (i.e., water, iodine, bone, or lead) attenuates the γ- or x-rays to about the same extent. However, attenuation per cm³ of those materials will still differ, in proportion to their density.

Fig. 6.9. Pair production. Under the influence of the positive charge of the nucleus, a γ-ray whose energy Eγ is more than 1.02 MeV annihilates and produces a pair of particles (an electron and a positron) that carry the balance of energy, Eγ − 1.02 MeV. The positron is subsequently annihilated in the manner described on p. 58.

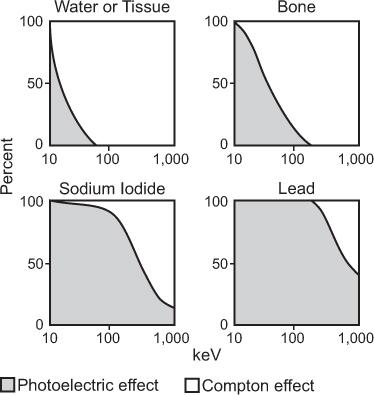
Relative Importance of the Three Processes The total interaction probability of an atom (atom) then, is the sum of the three probabilities, μ(atom), (atom), and (atom); that is, τ(atom) = σ(atom) + κ (atom) + (atom). Because of the complex and varying dependence of (atom) on γ-ray energy E and the atomic number Z of the material, generally one of these processes becomes the dominant mode of interaction for a given γ-ray energy and atomic number of the material. Figure 6.10 shows the relative importance of these processes for the 10-keV to 1 MeV energy range for four materials of great importance in nuclear medicine: water (tissue type), bone, sodium iodide [NaI(Tl)], and lead (Pb). In water or bone, most of the interaction of x- or γ-rays above 50 keV is through the Compton scattering. For lead, photoelectric interaction is the dominant mode of interaction even up to 1 MeV, although at these energies, Compton interaction does become important. In NaI(Tl), photoelectric effect is the dominant mode of interaction up to 300 keV.

Fig. 6.10. Relative contributions of photoelectric and Compton interaction to the total attenuation coefficient of water (tissue), bone, sodium iodide, and lead as a function of energy. In water and bone, almost all interactions above 50 keV are via the Compton scattering, whereas in sodium iodide and lead, the photoelectric effect is the dominant mode of interaction even up to 300 keV.

Interaction of Neutrons

Because neutrons do not have any electric charge, they do not experience the attractive or repulsive forces experienced by charged particles. Instead, these interact in billiard-ball fashion (direct hit) with the nuclei. When the energy of the neutrons is very low, they can easily enter a nucleus and may form radionuclides. Interaction of neutrons does not play a significant role in nuclear medicine, except in the production of some radionuclides by neutron-capture reactions (see Chapter 4), and therefore is not discussed here.

Key Points

1. Charged particles interact with matter through inelastic collisions and have a defined range of penetration R.

2. Range R increases with an increase in energy and decreases with an increase in mass and charge of the particle. It decreases with an increase in density of the interacting material. It increases as Q² but does not depend on the sign of the charge.

3. Linear energy transfer LET of a charged particle is an important parameter that affects biological damage.

4. Electrons and positrons interact in identical fashion except that positrons at the end of their range annihilate by combining with an electron. Annihilation produces two γ-rays of 511 keV. These γ-rays travel in opposite direction.

5. Bremsstrahlung is a secondary mechanism of interaction of charged particles. X-rays of various energies are produced when an electron or other charged particle passes in the vicinity of a nucleus.

6. X-rays and γ-rays do not have a well-defined range of interaction. Instead, half-value layer HVL is used to define a thickness of a substance that attenuates an x- or γ-ray beam by 50%.

7. For energies of interest in nuclear medicine, three mechanisms, photoelectric (all of the γ-ray energy given to an electron), Compton (γ-ray energy shared between an electron and a scattered γ-ray), and pair production (γ-ray energy is converted into an electron and positron pair) dominate the interaction of x- and γ-rays with matter.

8. Photoelectric effect is the dominant interaction for γ-ray energies up to 500 keV for high-atomic-number materials (>50) such as lead and NaI(Tl).

9. Compton scattering dominates in low atomic number materials such as soft tissue and bone above 100 keV.

10. Pair production is important only at high energies (1022 keV and above).

Questions

1. Arrange the following radiations in order of their penetrability: 1-MeV x-ray, 1-MeV electron, 1-MeV α particle, 50-keV characteristic x-ray, and 400-keV γ-ray.

2. List the factors on which the range of a charged particle depends.

3. If you know the range of a charged particle in water, what other information do you need to determine its range in another medium? If you know the linear attenuation coefficient of a γ-ray in water, will the same information let you determine the linear attenuation coefficient of another medium for the same γ-ray?

4. When a positron annihilates, what is the result?

5. The linear attenuation coefficients of 300 keV γ-rays for tissue, sodium iodide, and lead are approximately 0.12, 0.8, and 4.5 cm⁻¹, respectively. Determine the half-value layer for each material.

6. Determine the percentage transmission of 50 and 150 keV through 5 cm of tissue if the linear attenuation coefficients are 0.30 and 0.12 cm⁻¹, respectively.

7. Determine the percentage transmission of 140 keV through 10 cm heterogeneous layer of tissue consisting of 3 cm of soft tissue, 5 cm of lung tissue, and 2 cm of bone (linear attenuation coefficient is 0.12 cm⁻¹ for soft tissue, 0.21 cm⁻¹ for bone, and 0.04 cm⁻¹ for lung tissue).

8. The linear attenuation coefficients for lead at 140 and 750 keV are 22.7 and 1.13 cm⁻¹, respectively. Determine the percentage transmission through 3 mm lead.

9. Photoelectric effect generally decreases sharply with γ-ray energy. In what areas (energies) does this law break down?

10. Determine the energy of a back-scattered γ-ray if the energy of the primary γ-ray is one of the following: 100 keV, 500 keV, or 1 MeV.

11. What are the relationships among the linear attenuation coefficients of ice, water, and steam?

12. The linear attenuation coefficient of bone for 100-keV γ-rays is 0.2 cm⁻¹. Determine the percentage of 100-keV γ-rays that will pass through a 2-cm-thick bone without any interaction.

13. If in question 8, 80% of the interactions in bone are due to photoelectric effect and 20% due to Compton scattering, determine the percentage of 100-keV γ-rays that will interact through photoelectric and Compton interactions, respectively.

14. If a γ-ray interacts through pair production, what is the minimum energy it must have?

15. Why is LET important?

Radiation is known to produce a number of deleterious effects in a living system. Therefore, it is important to properly assess the benefits and risks to a patient from a given nuclear medicine procedure, ensuring that the benefits outweigh the risks, if any, by a significant margin. One factor that strongly influences the intensity or probability of radiation effects is the energy absorbed by the tissue (radiation dose). Therefore, the assessment of risk can be performed only if one knows the radiation dose that will be delivered to a patient by a particular procedure. This chapter describes the various methods for determining the radiation dose to a patient from internally administered radionuclides or radiopharmaceuticals. However, in the actual risk estimation, two other important factors, the relative biological effectiveness of the radiation and the tissue sensitivity, are also needed; these are discussed in Chapter 15. Radiation exposure and hazard from external radioactive source are discussed in Chapter 16.

General Comments on Radiation Dose Calculations

In nuclear medicine procedures, it is almost impossible to measure the radiation dose directly using any kind of radiation detector. Instead, this has to be calculated by using a variety of physical and biological data and mathematical equations specially developed for this purpose. It should be emphasized, however, at the outset that the accuracy of these calculations is complicated by several factors. First, even though the physical data needed can be acquired fairly accurately, it is difficult to obtain the biological data needed for these calculations with sufficient accuracy because these are, in practice, extrapolated from animal data or in some cases obtained from limited human data. Second, a variety of assumptions routinely made in these calculations (e.g., uniform distribution, instant uptake of the radiopharmaceutical in the given organ, or single exponential biological elimination) seldom holds true in practice. Third, radiation dose calculations are usually addressed to a hypothetical man known as the “standard man.” Various particulars such as the total body weight and weight of various organs of the standard man are given in Appendix E. These may differ appreciably in an actual case. Finally, the calculated dose is obtained by taking an average over a large volume (greater than 1 cm³) and therefore cannot be used to estimate radiation dose at cellular level (microdosimetry).

These factors, when combined, make radiation dose calculations susceptible to large errors. Hence, the radiation dose calculations presented here and elsewhere represent an average dose from a given procedure that may vary by a factor of 2, or even more, in an individual case.

Definitions and Units

Obviously, to calculate the radiation dose, one should know the meaning of radiation dose and radiation dose rate and their units of measurement.

Radiation Dose, D Radiation dose, or, more precisely, radiation absorbed dose, is a measure of the total energy absorbed from the radiation by 1 unit of mass of a substance. In the SI Unit System, absorbed dose is measured in gray (Gy). A gray equals 1 joule of energy absorbed/kilogram of a substance (J/kg). Two commonly used and derived units from gray are centigray (cGy = 10⁻² Gy) and milligray (mGy = 10⁻³ Gy). Its old unit is rad, which is a short notation for the radiation absorbed dose. A rad is defined as 100 ergs of absorbed energy per gram of a tissue or substance. One rad equals 1/100 Gy or equals a cGy and 1 Gy equals 100 rad.

Radiation Dose Rate, dD/dt Radiation dose rate, dD/dt, is defined as the amount of energy absorbed per unit time per unit of mass of tissue. Its units may be expressed in various ways, such as mGy (rad) per minute, cGy (rad) per hour, or Gy (rad) per day.

Parameters or Data Needed

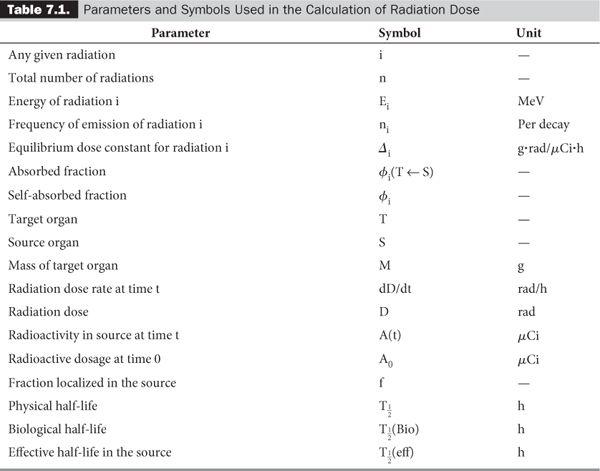
In a typical situation in nuclear medicine, a known amount of radioactivity of a radiopharmaceutical is administered to a patient. A certain fraction f of the radiopharmaceutical is then localized in the organ of interest. One is interested in knowing the radiation dose delivered to this organ and sometimes to various other organs as well. Two types of data are required for these calculations: one related to the decay characteristics of the radionuclide and one to the biological distribution and elimination of the radiopharmaceutical. Table 7.1 lists the various parameters needed for these calculations, together with the units and symbols used here. Some parameters have been defined in Chapters 2 and 3; some are self-evident, and the others are discussed in this chapter. I have retained the old units because a large amount of the data needed in these calculations is still in old units. It is easier to convert the final equations, tables, or results in the SI units, which I have done here at the appropriate places.

Calculation of the Radiation Dose

To calculate the radiation dose, one has to determine the average amount of energy absorbed by 1 g of tissue of a target (organ of interest) from the total energy released by the decay of a given amount of radioactivity. Because x- or γ-rays are more penetrating than particulate radiation, a small x- or γ-ray emitting source, localized at any site in the body, irradiates practically every organ of the body. For example, an x- or γ-ray emitting radionuclide localized only in the liver (source S) delivers the radiation dose to all other organs (targets T) of the body in addition to the liver. Thus, if a radiopharmaceutical is localized in multiple organs (sources), the radiation dose from each source to each organ (target) has to be calculated before the final determination of the radiation dose to each organ can be made by adding all contributions. The following four steps are involved in the radiation-dose determinations:

1. Calculation of the rate of energy emission (erg/h) of the various types of radiation emitted by the radionuclide in the source volume.

2. Calculation of the rate of energy absorption from these radiations by the target volume.

3. Calculation of the average dose rate, dD/dt.

4. Calculation of the average dose D.

This method of radiation dose calculation is known as the absorbed fraction method. The first three steps require mainly physical data such as decay characteristics, organ shape and size, and so on, whereas the fourth step requires biological distribution data.

Step 1: Rate of Energy Emission Let us first consider a radionuclide that emits only one type of radiation (emission frequency = 1) of energy E (MeV) per decay. One microcurie (3.7 × 10⁴ decay/s) of this radionuclide will, therefore, emit energy at a rate of 3.7 × 10⁴ × E MeV/s. If we change the unit of energy from MeV to erg (1 MeV = 1.6 × 10⁻⁶ erg) and the unit of time from second to hour (1 h = 3600 s), the rate of energy emission by this radionuclide becomes equal to 3.7 × 10⁴ × 1.6 × 10⁻⁶ × 3600 × E erg/(h · μCi), or 213E erg/(h · μCi).

In the case of a radionuclide that emits more than one radiation, say 1, 2, 3, …, n, with emission frequencies n₁, n₂, n₃, …, n_n and energies of E₁, E₂, E₃, …, E_n, respectively, the rate of energy emission for each type of radiation will be equal to 213n₁E₁ erg/(h · μCi) for radiation 1, 213n₂E₂ erg/(h · μCi) for radiation 2, and so on.

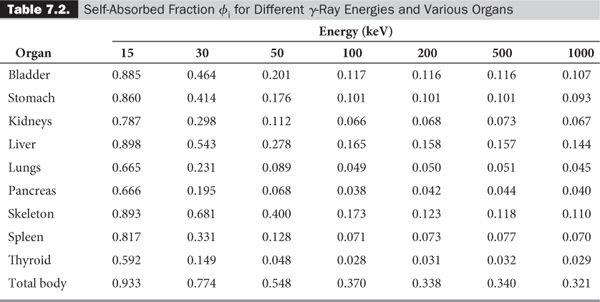
Step 2: Rate of Energy Absorption To calculate the rate of absorption of energy by a target volume T from a radionuclidic distribution in a source volume S, we have to define a new quantity known as the absorbed fraction, φ(T←S). The absorbed fraction φ_i(T←S) is defined as the ratio of energy absorbed by a target volume T from a radiation i to the amount of energy released by a radionuclidic distribution in volume S in the form of radiation i. In other words,

In most problems encountered in nuclear medicine, the radioactivity is distributed within the target volume T itself (i.e., T is the same as S). In that case, the absorbed fraction is known as the self-absorbed fraction and is expressed simply as φ_i.

Once φ_i(T←S) is known, the rate of energy absorption by a target volume T is simply obtained by multiplying the rate of energy emission of radiation i (from step 1, 213n_iE_i) by the absorbed fraction φ_i(T←S), or

Rate of energy absorption by the target volume from radiation i = 213n_iE_i × φ_i(T←S)