Fig. 1.1
Photon propagation within turbid media. For a clear description, the three components are depicted separately: a unscattered photons; b snake photons; c multiply scattered photons
1.1.2 Physical Properties of Photons
There are a few physical effects that need to be considered regarding the photon components mentioned in the previous section. These effects are associated with the spectral , spatial, temporal , and polarization properties of the illumination light propagating through turbid media. The spectral property describes the frequency shift of the illumination photon flux. The deviation (spreading) of the illumination photon flux in space is described by the spatial property of scattered photons. The temporal property describes the time-induced delay (pulse spreading) of the illumination photon flux. The polarization property describes the phase relationship of individual photons in the illumination photon flux. All these effects are mutually connected and are independent of the light source used except for the temporal effect, which cannot be detected with a continuous-wave laser source (i.e., a pulse light source is needed).
The spectral effect is demonstrated in Fig. 1.2a for pulsed illumination. The spectral effect can only be considered if inelastic collisions take place [9]. After the illumination pulse passes through a turbid medium the snake and multiply scattered photons will have their frequencies shifted from the unscattered component. The magnitude of the spectral shift, Δω, induced depends on the number of scattering events experienced by an individual photon. That is, the larger the number of scattering events experienced the larger the spectral shift incurred. Most of the present research tends to treat collisions as an elastic process, which means that there is no energy transfer from photons to scattering particles, so no spectral change occurs (i.e., Δω = 0). This situation simplifies the problem of modeling, since it ignores scattering phenomena such as Mandel’stam-Brillouin and Raman scattering [9]. Although no scattering event is purely elastic, in most situations this is a good and reasonable approximation to be made since the frequency shift , Δω, is small. Throughout this book, we assume that there is no frequency shift.
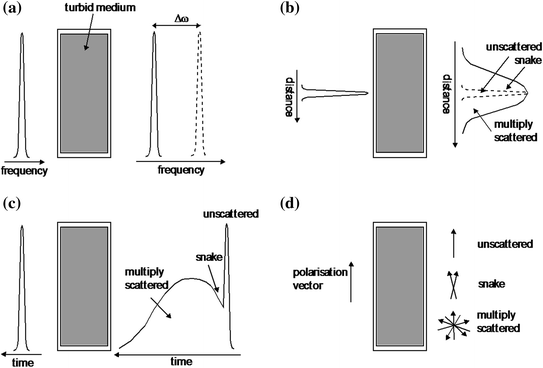

Fig. 1.2
Schematic demonstration of four physical effects of photons propagating through turbid media: a spectral shift; b spatial broadening; c temporal broadening; d polarization degradation
The spatial spreading of an incident beam with a Guassian beam profile is illustrated in Fig. 1.2b. The collected unscattered portion of the illumination beam is illustrated with dashed lines. Snake and multiply scattered photons cause the diffraction pattern generated by the unscattered photons to broaden, since they travel along paths that are different from the unscattered straight through path (see Fig. 1.1). The amount of spatial broadening of the illumination beam is determined by the characteristics of the turbid media at the wavelength of illumination. The statistically different propagation paths of unscattered and scattered photons are the bases of the angle-gating principle discussed in Chap. 5.
The temporal properties can only be considered when a pulsed illumination beam is considered (Fig. 1.2c). An incident pulse can broaden (in the time domain) when the pulse undergoes its transition through turbid media. The unscattered photons are the first to arrive, followed closely by the snake photons, and at a later time the multiply scattered photons arrive. The turbid media characteristics at the wavelength of illumination determine the amount of delay (temporal pulse broadening ) induced between the unscattered, snake, and scattered photons.
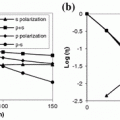
Figure 1.2d demonstrates the change in the polarization vector of an illumination beam propagating through turbid media. The state of polarization for the illumination beam (for example, defined by the vertical polarization vector in Fig. 1.2d) is maintained with unscattered photons. Snake photons lose some degree of the illumination polarization state, and the multiply scattered photons suffer substantial depolarization. That is, the orientation of the polarization vector is partially or completely random. The magnitude of the direction change in the polarization vector is determined by the characteristics of turbid media at the wavelength of illumination.
As summarized in Table 1.1, these four effects (spectral, spatial, temporal, and polarization) provide direct distinguishable differences between the unscattered, snake, and scattered components, which can be taken advantage of when a particular detection scheme is used. One can assume that unscattered photons and snake photons are those necessary to create an informative high resolution and high contrast image. Thus, methods for detecting only unscattered and snake photons (the coherent component of the illumination beam) that carry more information about the embedded object, while the multiply scattered photons (the incoherent component of the illumination beam) are suppressed, have been used in imaging through turbid media. However, it should be noted that images may be reconstructed from the multiply scattered photons if the phase and amplitude of the scattered photons are known at many points in space. However, the reconstruction of images from multiply scattered photons, known as the inverse scattering problem [10], remains a difficult experimental and theoretical problem to be overcome in imaging through turbid media.
Table 1.1
Physical difference between unscattered and scattered photons after propagating through a turbid medium
Unscattered photons provide | Scattered photons provide |
|---|---|
• Early arrival time | • Late arrival time |
• Same coherence | • Low coherence |
• Same polarization | • Depolarized |
• Same direction | • Different direction |
1.2 Microscopic Imaging Through Tissue-Like Media
Imaging an object embedded in a turbid medium has attracted substantial interest since it is potentially related to applications in early cancer detection. Research work in this field can be classified into two categories: transillumination imaging, in which case a parallel beam probe is used [11–20] and microscopic imaging, in which a microscopic objective is used for illumination as shown in Fig. 1.3 [21–58].
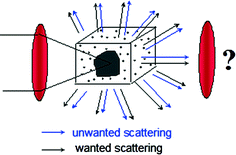

Fig. 1.3
Microscopic imaging through a turbid medium in which an object is embedded
In an optical microscope, an object embedded in a turbid medium is illuminated by an objective lens of a range of the illumination angle. The optical signal in each direction comprises two parts; one part is scattered by the embedded object and the other is scattered by the scattering medium surrounding the object. The former is a wanted signal carrying information about the object and forms an image by an imaging objective, while the latter is unwanted as it mainly contributes to the background of an image. As a result of using an illumination objective, the two parts of the signal superpose each other, which degrades the image quality. A number of approaches have been proposed to obtain useful images through significant depths of a turbid medium. A gating method means the suppression of the unwanted scattered signal. The gating methods currently available to selectively suppress the scattered photons based on the properties in Table 1.1 are time-gating [8], which relies on the utilization of an ultrashort pulsed beam, coherence-gating [26], which relies on the degree of coherence of photons, polarization-gating [17], which relies on the polarization-state of photons, and angle-gating [33–36], which relies on the path deviation of the scattered photons. Although all of these gating mechanisms can be employed in any imaging system, the efficiency of these methods depends on a particular imaging system. Transillumination imaging systems which use a parallel beam probe can give images of millimeter resolution [6, 7]. To obtain an image of micrometer resolution, a microscope objective is necessary. In this case, time-gating may become less efficient due to the large range of illumination angles. However, angle-gating, polarization-gating, coherence-gating , and fluorescence-gating are important in microscopic imaging. In addition, the use of an objective leads to a focal region of an intensity that is high enough to produce nonlinear excitation such as two-photon excitation [27]. Because the strength of the nonlinear signal is mainly determined by the ballistic photons, any nonlinear excitation process under a microscope can be used to suppress scattered photons, which results in a unique nonlinear-gating mechanism in microscope imaging through turbid media [47].
However, using an objective lens in a microscopic imaging system raises the question of which numerical aperture of an objective is suitable for imaging. According to the imaging theory based on Born’s approximation, which ignores the multiple scattering in a turbid medium, a high numerical aperture objective lens can provide high diffraction-limited resolution [1–5]. Born’s approximation is applicable to the case in which the optical thickness n, defined as the thickness of a turbid medium divided by the scattering mean free path length, is less than one. On the other hand, a low numerical aperture objective can suppress scattered photons that statistically travel at high angles. Both arguments are based on the assumption that ballistic light is dominant in forming an image. When a turbid medium is thick, e.g., when n > 10, the strength of the unscattered light/photons may be too weak to be detected, particularly in the presence of detector noise. In this situation scattered light has to be included in constructing an image. An important question raised here is what role the scattered light plays in constructing an image. To answer this question, the relationship of scattered photons to image resolution should be investigated. In other words, suitable numerical aperture of the objective lens to be used in a particular microscopic imaging system for high-quality imaging should be investigated.
Turbid media, typically biological tissue, always exhibits complex characteristics as it has complex structures and is composed of various components. Usually, it shows a multiple-layer structure rather than a single-layer structure and consists of multiple sizes of scatterers rather than a single size. Furthermore, an inhomogeneous feature may exist because of the aggregation effect of the scatterers. Such structural, size, or aggregation features from turbid media will greatly influence images under a microscope.
1.3 Monte Carlo Simulation
Microscopic imaging study through tissue-like media is an important and significant topic since it is potentially related to the use of microscopy in noninvasive imaging and spectroscopy of biological tissues, and thus the potential applications in early medical diagnoses of tumors [59]. However, the analysis of microscopic imaging in a highly scattering turbid medium is complicated by the basic incompatibility between the techniques developed for modeling diffraction-limited optical systems [1–5] and those developed for modeling light propagation in multiply scattering media [9, 60]. For a medium in which the concentration of the scatterers is high enough that multiple scattering cannot be neglected, the diffraction theory fails. The single-scattering theory based on the Born approximation is not appropriate for describing light transport in biological soft tissues thicker than a few tens of micrometers due to the strong scattering in the wavelength range of 0.6–1.0 μm [61]. Some already obtained analytical expressions based on the radiative transfer theory describing the effects of multiple scattering on the performance of imaging systems are either based on the small-angle approximation [62], which is applicable only to a medium containing a relatively low concentration of particles with size much larger than a wavelength, or on the evaluation of a multidimensional integral that is practical to evaluate only for low orders of scattering [63].
Biological tissue is a highly optical scattering material; it contains dense concentrations of anisotropic scatterers and the inhomogeneous cellular structures with scatterers are usually of optical wavelength order. Because of the optical dense feature in biological tissue, the diffuse approximation of the radiative transfer theory can be applied [64]. Since this method deals with mainly forward scattered photons, it is hardly applicable to a microscopic imaging system in which photons scattered into a large angle affect the imaging performance significantly.
The Monte Carlo method is easy to apply and flexible to handle complex geometries and inhomogeneity. By tracing the behavior of various types of photons, ballistic, snake, multiply forward-scattered/diffuse photons, it is helpful to gain an understanding of the underlying physics in photon migration through a tissue-like turbid medium and imaging resolution in an optical system. Therefore, in the recent three decades, Monte Carlo simulation has been given considerable attention and widely applied to the tissue optics [65]. In the study of microscopic imaging of an object deeply embedded in a tissue-like sample, the Monte Carlo method is one that can be successfully and flexibly combined with microscopic systems for investigating imaging performance and image reconstruction [23, 29, 30, 33, 34, 37, 41, 42, 46–48, 50–58, 65].
The Monte Carlo method can be conceptually understood to be a stochastic technique, which means it is based on the use of random numbers and probability statistics to investigate problems, although an accurate, complete, and concise definition to characterize it is difficult to construct [66, 67]. A definition given by Lux et al. [68] may give us a mathematical understanding: in all the applications of the Monte Carlo method, a stochastic model is constructed in which the expected value of a certain random variable (or of a combination of several variables) is equivalent to the value of a physical quantity to be determined. This expected value is then estimated by the average of several independent samples representing the random variable introduced above. For the construction of a series of independent samples, random numbers following the distributions of the variable to be estimated are used.
In the case of Monte Carlo simulation of photon propagation through a scattering medium, individual photons are supposed to experience events of scattering and absorption according to the local values of the optical properties of the scattering medium. The individual photon paths can be simulated by considering the probability distribution of two random variables, the step length and the scattering angle. The probability distributions of the random variables of the step length and scattering angle, respectively, describe the step size a photon may take between two successive photon-medium interaction sites and the angles of deflection a photon may experience when a scattering event occurs. These two probability functions can be derived from Beer’s law and the Mie scattering theory [9, 60]. The Monte Carlo simulation then is performed by tracing the random walks that a large number of photons make based on the statistical sampling from the probability distributions in each scattering event.
1.4 Direct and Inverse Approaches
Imaging modeling usually includes two aspects, direct and inverse approaches. In the former approach, one simulates the final image if the object condition and the property of an imaging system are given. In the latter approach, one reconstructs the object function if an image is given. Given that no imaging system is perfect, any measured image shows less detail than the original object. Using an inverse approach, one can enhance the image quality such as resolution and contrast. To this end, it is necessary to have a defined mathematical relation between an object and its image. For example, the imaging theory based on light diffraction shows that a convolution relation holds under the paraxial approximation [1–5].
However, as discussed in the previous section, due to the complicate nature caused by multiple scattering in a turbid medium, conventional image modeling methods based on the diffraction theory [1–5] are not applicable. The Monte Carlo simulation method involving the Mie theory is one of the useful tools for imaging modeling in a turbid medium, because it provides insight into light interaction with scattering particles. In this aspect, the Monte Carlo method is used as a direct approach. However, this type of simulation may not be applicable in image reconstruction because there is no defined mathematical relation between an object and its image. Another problem associated with image modeling based on the Monte Carlo method is time-consuming because a large number of incident photons are required to ensure a required accuracy. The requiring of computational time increases significantly when images of complicated objects embedded in a turbid medium are modeled.
To address these problems, the concept of the effective point spread function (EPSF ) has been introduced in transillumination imaging through turbid media. Recently, this concept has been generated to Monte Carlo simulation in a turbid medium under an optical microscope [42]. It should be pointed out that defining a point spread function (PSF) in a turbid medium is not straightforward. If there is no turbid medium, a PSF is the image of a point object and is a measure of image blurring through an imaging system. It determines resolution of an imaging system and therefore is independent of the property of an object. As a result, under Born’s approximation [1, 2], the image of an object can be obtained from the convolution of a PSF with an object function. If an object is embedded in a turbid medium, it is difficult to use the concept of a point object because of the existence of scattering particles which are in the range of 0.1–1 μm in diameter. Further, a PSF that includes only the property of a microscope may not be adequate because the multiple scattering effect may severely distort the image of an embedded object. Therefore, the property of a microscope as well as the property of scattering particles should be included in an effective PSF for a microscope.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree