(1)
Department of Mathematics and Statistics, Villanova University, Villanova, PA, USA
10.1 Introduction
Magnetic resonance imaging, or MRI, is an imaging technique that has grown alongside CT and that, like CT, has produced Nobel laureates of its own. Where the physics of CT is fairly straightforward — X-rays are emitted and their changes in intensity measured — MRI is based on the generation of a complex of overlapping, fluctuating electromagnetic fields that must be precisely controlled. Mathematically, the effects of the electromagnetic fields on the atomic nuclei in the sample being studied are modeled with differential equations. The Fourier transform is the primary tool for analyzing the electrical signals generated by the motions of atomic nuclei under the influence of these fields.
Clinically, MRI is safer than CT for most patients since it involves no radiation. The magnetic fields involved operate at frequencies in the radio band range. (In fact, to the patient undergoing an MRI exam, it sounds like listening to a very loud, very weird radio station.) In order to emphasize the safety and to discourage confusion, the original appellation of nuclear magnetic resonance imaging (nMRI) was shortened. On the downside, an MRI machine is expensive to purchase, operate, and maintain. Also, the intensity of the magnetic fields can rule out the procedure for some patients, including those with certain metallic implants.
Magnetic resonance imaging is a wide-ranging and continually developing field of study and practice, and is the subject of an extensive body of literature. Consequently, in this chapter we present only a brief overview of some of the basic principles involved in MRI, emphasizing aspects of the underlying mathematics. For a reader wishing to undertake a more intensive investigation of MRI, some possible starting points are the article [26] and the books [21, 5, 20], and [33].
Two basic descriptions of the phenomenon known as nuclear magnetic resonance (NMR) were published in 1946, one by a team of researchers led by Felix Bloch (1905–1983) and the other by a team headed by Edward Purcell (1912–1997). Bloch’s point of view (see [4]) is based on principles from classical physics and adopts an aggregate approach, looking at the net magnetization of the nuclei in a sample. Purcell’s description ([41]) is grounded in quantum physics and examines the magnetic effects at the level of an individual nucleus. It is perhaps ironic that Bloch was trained as a quantum physicist (his doctoral advisor was Werner Heisenberg ), while Purcell was a classical physicist (his doctoral advisor was John van Vleck ). In 1952, Bloch and Purcell were joint recipients of the Nobel Prize for Physics.
For several decades after Bloch and Purcell established the physical basis for studying NMR, the primary application was to chemical spectroscopy, and it was only around 1970 that the possibility of using NMR for imaging was realized. Paul Lauterbur (1929–2007) is credited with introducing the idea of using gradient magnetic fields to achieve spatial resolution of the radio signal emitted by a magnetized sample. Applying his technology to a setup consisting of test tubes of heavy water sitting inside a beaker of regular water, he produced the first images that could distinguish between two different kinds of water. (See [34].) Peter Mansfield (1933 – ) advanced Lauterbur’s work by developing techniques for mathematically analyzing the radio signals, including a technique known as echo-planar imaging that speeds up the imaging process. (See [38].) Lauterbur and Mansfield were jointly awarded the 2003 Nobel Prize for Medicine and Physiology.
10.2 Basics
The nucleus of a hydrogen atom, a chemical element found in abundance in the human body, possesses a property known as spin. Conceptually, one can think of the single proton that comprises this nucleus as a tiny spinning top, rotating about an axis. This property brings with it a magnetic effect, whereby the spinning proton behaves like a bar magnet with north and south poles. As the little magnet spins, it generates an electrical signal. In the absence of other factors, there is no preferred choice for the axis around which the proton spins nor for the orientation of this axis within three-dimensional space. Within a sample of hydrogen-rich tissue, then, the distribution of spins will be random and the resulting signals will cancel each other out.
If, however, the sample is immersed in a strong external magnetic field having a fixed direction, then the spin axes of the hydrogen protons will tend to align either in the same direction as the external field or in the opposite direction. There will be some of each, but measurably more in the same direction as the field, as this state involves a lower energy level. To be more precise, the axes of the spinning hydrogen protons will not align exactly with the external field but will precess, or wobble, about it, much as a spinning top whose axis is not vertical precesses about the vertical as it spins. Due to the precession, the magnetic moment of any one particular nucleus will have a vector component that is perpendicular to the direction of the external field. However, because there is no preferred phase for the precession, the phases of the various nuclei in the sample will be randomly distributed and, as a result, the sum of these components will cancel out. Over the whole sample, then, the effect is of an aggregate nuclear magnetic moment that is aligned in the same direction as the external magnetic field.
In this equilibrium state, with all of the nuclei behaving in basically the same way, exhibiting a sort of herd mentality, no useful electrical signal will be generated. To create a signal, a second magnetic field is introduced, one that oscillates in a plane perpendicular to the static external field. This new field causes the alignment of the nuclei to flip out of the equilibrium state. As the nuclei begin to precess about a new axis, the specifics of which depend on the strength and duration of the new field, the aggregate nuclear magnetic moment develops a nonzero net component transverse to the static magnetic field. After a certain amount of time, this second field is cut off and the nuclei relax back to their previous state. There are two aspects to this relaxation.
As the net transverse component of the magnetic moment precesses, it induces an electromotive force (emf) in a coil that surrounds the sample. At the same time, with only the static field in effect, the nuclei gradually become de-phased in the transverse direction as they move toward equilibrium. Essentially, the net transverse magnetization describes a decaying wave, the rate of decay of which can be measured by analyzing the resulting induced emf. This process is known as spin–spin, or T 2, relaxation.
While the transverse component of the nuclear magnetic moment decays to zero, the component in the direction of the static magnetic field returns, asymptotically, to its equilibrium level. This process is called spin–lattice, or T 1, relaxation. As we shall see, the rate at which this process evolves can be measured through careful manipulation of the second magnetic field and the analysis of an electrical signal induced by the motion of the aggregate nuclear magnetic moment.
Different tissue types, or, more precisely, magnetized nuclei contained inside different chemical environments, have different T 1 and T 2 relaxation rates, the measurements of which reveal the types of material present within the sample. To resolve this information spatially, so that an image can be created showing the location within the sample of each type of tissue, additional magnetic fields, known as gradients, are introduced to the experiment. This is discussed in what follows.
At the molecular and atomic level, quantum effects certainly exist, but the classical approach outlined here is more feasible when it comes to designing practical machines to implement the system. So, with this conceptual framework in mind, we turn our attention to the mathematical model introduced by Bloch in 1946.
10.3 The Bloch equation
In an MRI machine, a strong, uniform, and steady magnetic field, B 0, is generated by running an electrical current through a large coil. In clinical applications, the direction of the field B 0 is aligned along the length of the patient’s body, which direction is taken as the z-axis of a Cartesian coordinate system and is also referred to as the longitudinal direction. The magnitude or strength of B 0, denoted by B 0 (without the boldface type), is usually about 0. 5 tesla in practice.
Denote the aggregate magnetic moment of the nuclei in a sample by M(t, p), or simply by M if the context is understood. This is a vector function that depends both on time t and on the location p within the sample. The coordinate functions of M are denoted by M x , M y , and M z . That is, for each time t and each point p in the sample,
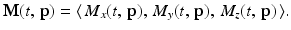
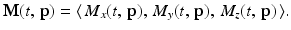
As discussed above, in the presence of the static magnetic field B 0 alone, the equilibrium nuclear magnetization of the sample is directed along the z-axis. That is, at equilibrium, 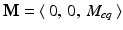 , where M eq is the magnitude of this vector.
, where M eq is the magnitude of this vector.
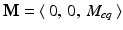 , where M eq is the magnitude of this vector.
, where M eq is the magnitude of this vector.In addition to the steady magnetic field B 0, a variety of other magnetic fields are introduced. These additional fields alter the magnitude and alignment of the nuclear magnetization of the sample and vary both temporally and spatially. Here, we use B = B(t, p) to denote the total external magnetic field experienced by the sample at time t and location p.
The Bloch equation models the rate of change over time of the magnetic moment of the nuclei at each point in the sample. With the notation just introduced, the equation is
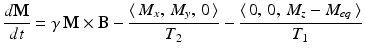
where γ, T 1, and T 2 are constants. For reasons that will be clear soon, the value of γ is related to the resonant frequency of the system, while T 1 and T 2 are called the relaxation times.
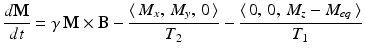
(10.1)
In the presence only of the static magnetic field 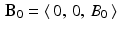 , directed along the z-axis, the Bloch equation simplifies to the system of equations
, directed along the z-axis, the Bloch equation simplifies to the system of equations
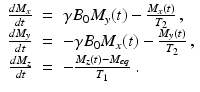
The first two of these equations define a first-order linear system with a constant coefficient matrix that can be solved using standard eigenvalue–eigenvector methods. The third equation can be treated either as a separable equation or as a first order linear equation. The upshot of this analysis is that
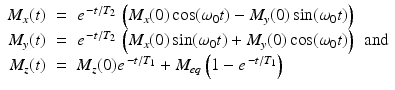
where 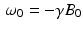 . Thus, we see that, for times t that are large compared to the value of T 1, the longitudinal component M z (t) tends toward the equilibrium magnetization M eq . Meanwhile, in the transverse plane, as the xy-plane is called in this context, the magnetic moment of the nuclei rotates, or precesses, about the z-axis with angular frequency
. Thus, we see that, for times t that are large compared to the value of T 1, the longitudinal component M z (t) tends toward the equilibrium magnetization M eq . Meanwhile, in the transverse plane, as the xy-plane is called in this context, the magnetic moment of the nuclei rotates, or precesses, about the z-axis with angular frequency 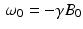 radians per second, known as the Larmor frequency. The constant γ , called the gyromagnetic ratio, typically has a value of about 2. 68 × 108 radians per second per tesla, or, equivalently, about 42.6 megahertz (MHz) per tesla. (One hertz is one cycle per second, or 2π radians per second.) Thus, in a typical MRI experiment, the Larmor frequency lies in the radio frequency band. In comparison, X-rays have a much higher frequency of about 3 gigahertz.
radians per second, known as the Larmor frequency. The constant γ , called the gyromagnetic ratio, typically has a value of about 2. 68 × 108 radians per second per tesla, or, equivalently, about 42.6 megahertz (MHz) per tesla. (One hertz is one cycle per second, or 2π radians per second.) Thus, in a typical MRI experiment, the Larmor frequency lies in the radio frequency band. In comparison, X-rays have a much higher frequency of about 3 gigahertz.
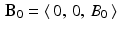 , directed along the z-axis, the Bloch equation simplifies to the system of equations
, directed along the z-axis, the Bloch equation simplifies to the system of equations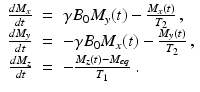
(10.2)
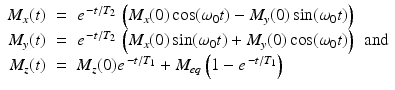
(10.3)
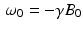 . Thus, we see that, for times t that are large compared to the value of T 1, the longitudinal component M z (t) tends toward the equilibrium magnetization M eq . Meanwhile, in the transverse plane, as the xy-plane is called in this context, the magnetic moment of the nuclei rotates, or precesses, about the z-axis with angular frequency
. Thus, we see that, for times t that are large compared to the value of T 1, the longitudinal component M z (t) tends toward the equilibrium magnetization M eq . Meanwhile, in the transverse plane, as the xy-plane is called in this context, the magnetic moment of the nuclei rotates, or precesses, about the z-axis with angular frequency 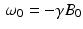 radians per second, known as the Larmor frequency. The constant γ , called the gyromagnetic ratio, typically has a value of about 2. 68 × 108 radians per second per tesla, or, equivalently, about 42.6 megahertz (MHz) per tesla. (One hertz is one cycle per second, or 2π radians per second.) Thus, in a typical MRI experiment, the Larmor frequency lies in the radio frequency band. In comparison, X-rays have a much higher frequency of about 3 gigahertz.
radians per second, known as the Larmor frequency. The constant γ , called the gyromagnetic ratio, typically has a value of about 2. 68 × 108 radians per second per tesla, or, equivalently, about 42.6 megahertz (MHz) per tesla. (One hertz is one cycle per second, or 2π radians per second.) Thus, in a typical MRI experiment, the Larmor frequency lies in the radio frequency band. In comparison, X-rays have a much higher frequency of about 3 gigahertz.As 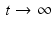 , the transverse component of the nuclear magnetization tends to 0, which does not mean, however, that the precession of the individual nuclei about the z-axis ceases. Rather, these rotations go out of phase with each other so that the distribution of the individual moments becomes random and the aggregate transverse component tends to zero. In the equilibrium state, each nucleus tends to precess with angular frequency ω 0 about the z-axis with longitudinal component M eq . A useful image, again, is that of a spinning top whose axis is not vertical but precesses about the vertical with a fixed frequency.
, the transverse component of the nuclear magnetization tends to 0, which does not mean, however, that the precession of the individual nuclei about the z-axis ceases. Rather, these rotations go out of phase with each other so that the distribution of the individual moments becomes random and the aggregate transverse component tends to zero. In the equilibrium state, each nucleus tends to precess with angular frequency ω 0 about the z-axis with longitudinal component M eq . A useful image, again, is that of a spinning top whose axis is not vertical but precesses about the vertical with a fixed frequency.
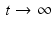 , the transverse component of the nuclear magnetization tends to 0, which does not mean, however, that the precession of the individual nuclei about the z-axis ceases. Rather, these rotations go out of phase with each other so that the distribution of the individual moments becomes random and the aggregate transverse component tends to zero. In the equilibrium state, each nucleus tends to precess with angular frequency ω 0 about the z-axis with longitudinal component M eq . A useful image, again, is that of a spinning top whose axis is not vertical but precesses about the vertical with a fixed frequency.
, the transverse component of the nuclear magnetization tends to 0, which does not mean, however, that the precession of the individual nuclei about the z-axis ceases. Rather, these rotations go out of phase with each other so that the distribution of the individual moments becomes random and the aggregate transverse component tends to zero. In the equilibrium state, each nucleus tends to precess with angular frequency ω 0 about the z-axis with longitudinal component M eq . A useful image, again, is that of a spinning top whose axis is not vertical but precesses about the vertical with a fixed frequency.The constant T 1 is called the spin–lattice relaxation time and reflects the dissipation in energy away from the spinning nuclei (the spin system) as the atomic and molecular structure (the lattice) of the sample settles into the equilibrium state. The spin–spin relaxation time, as T 2 is known, reflects the randomization of the phases of the spinning nuclei as the aggregate transverse component goes to 0. Thus, T 2 reflects the dissipation of energy within the spin system.
10.4 The RF field
No signal is emitted by the atomic nuclei so long as they are subjected only to the static magnetic field B 0. To knock them out of this equilibrium, a radio frequency (RF) transmitter is used to apply a linearly polarized RF magnetic field
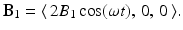 This field is generated by sending an oscillating electrical current through a transmitting coil that surrounds the sample. The field B 1 oscillates along the x-axis with frequency ω, called the irradiation frequency, and is effectively the sum of two circularly polarized fields that oscillate in the xy-plane with the same frequency but in opposite directions. Namely,
This field is generated by sending an oscillating electrical current through a transmitting coil that surrounds the sample. The field B 1 oscillates along the x-axis with frequency ω, called the irradiation frequency, and is effectively the sum of two circularly polarized fields that oscillate in the xy-plane with the same frequency but in opposite directions. Namely,
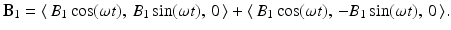 Physically, the nuclei, and, hence, the aggregate magnetic moment, are significantly affected only by the circular field that oscillates in the same direction as the precession. This means that we may take
Physically, the nuclei, and, hence, the aggregate magnetic moment, are significantly affected only by the circular field that oscillates in the same direction as the precession. This means that we may take
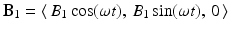
to be the effective RF magnetic field.
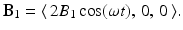
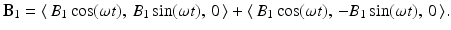
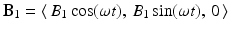
(10.4)
The magnetic field in the longitudinal direction consists of the static field B 0 and the contribution from the gradient field, B G , discussed below. The overall magnetic field applied to the sample is, then,
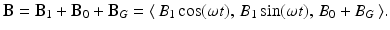
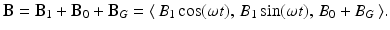
(10.5)
The duration of the RF pulse is short relative to the values of T 1 and T 2, sufficiently so that we may ignore the T 1 and T 2 terms when we analyze the Bloch equation (10.1) during this time interval. So, in this context, the Bloch equation leads to a system of linear differential equations with nonconstant coefficients; specifically,