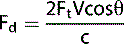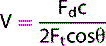Chapter 11 Physical principles of Doppler ultrasound

INTRODUCTION

This chapter provides the basic introduction to the physical principles and application of Doppler ultrasound in practice. The application of Doppler in ultrasound was first introduced in the 1980s and since then this technique has expanded in all specialist fields of practical ultrasonography.

A Doppler ultrasound is a non-invasive test that can be used to investigate movement and particularly evaluate blood flow in arteries and veins. It can also be used to provide information regarding the perfusion of blood flow in an organ or within an area of interest. A more recent application is the investigation of tissue wall motion when evaluating the heart (see Chapter 14 on New technology).

Doppler ultrasound can be used to diagnose many conditions, including:

• heart valve defects and congenital heart disease

• a blocked artery (arterial occlusion)

• narrowing (stenosis) of an artery

• blood clots (deep vein thrombosis)

• varicose veins (venous insufficiency)

• arteriovenous malformations

• movement of the cardiac wall.

THE DOPPLER PRINCIPLE

The Doppler principle is named after the mathematician and physicist Christian Johann Doppler who first described this effect in 1842 by studying light from stars. He demonstrated that the colored appearance of moving stars was caused by their motion relative to the earth. This relative motion resulted in either a red shift or blue shift in the light’s frequency. This shift in observed frequencies of waves from moving sources is known as the Doppler effect and applies to sound waves as well as light waves.

The Doppler Effect

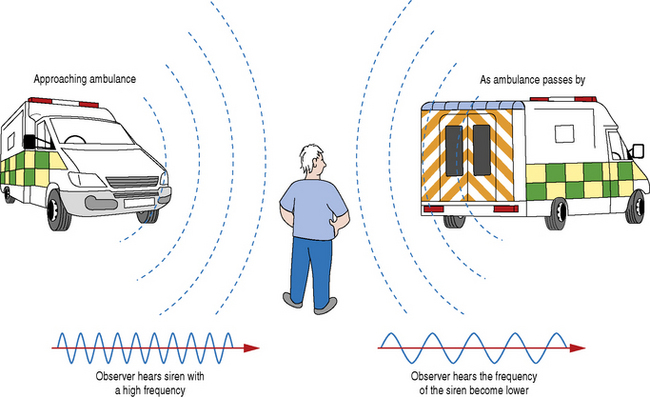
An everyday example which demonstrates the Doppler effect is highlighted in Figure 11.1. We are all aware that the pitch of an ambulance siren changes as we stop and listen to it as it drives by. The frequency that reaches you is higher as the ambulance approaches and lower as the ambulance passes by. This is a consequence of the Doppler effect.

Fig. 11.1 The consequence of the Doppler effect on the relative emitted frequency of an ambulance siren as it drives by. The frequency of the approaching ambulance siren appears higher compared to the frequency of the siren as the ambulance passes by which appears lower

What is happening is that the sound waves are compressed when an object producing sound is moving in the same direction as the waves. The listener (observer) therefore receives shorter wavelengths. However, when the source of sound has passed the listener, the waves are now moving in the opposite direction (away from the listener), the wavelength becomes longer and the listener therefore hears a change in frequency.

This Doppler effect is utilized in ultrasound applications to detect blood flow by analyzing the relative frequency shifts of the received echoes brought about by the movement of red blood cells.

THE DOPPLER EFFECT APPLIED TO DIAGNOSTIC ULTRASOUND

The Doppler effect in diagnostic imaging can be used to study blood flow, for example, and provides the operator with three pieces of information to determine:

• Presence or absence of flow

• Direction of blood flow

• Velocity of blood flow.

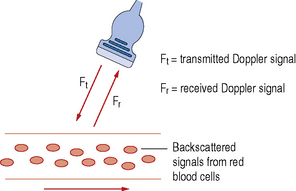
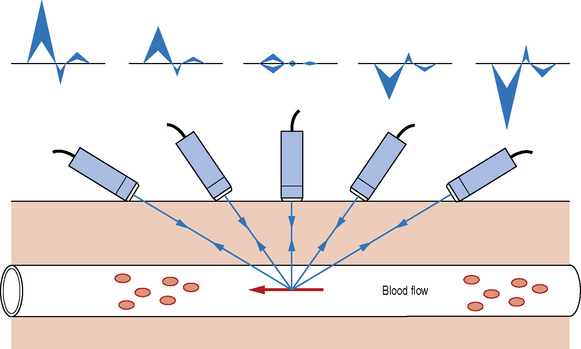
The transducer acts as both a transmitter and receiver of Doppler ultrasound. When using Doppler to investigate blood flow in the body, the returning backscattered echoes from blood are detected by the transducer. These backscattered signals (F_r) are then processed by the machine to detect any frequency shifts by comparing these signals to the transmitted Doppler signals (F_t). The frequency shift detected will depend on two factors, namely the magnitude and direction of blood flow (see Fig. 11.2).

Fig. 11.2 An ultrasound transducer interrogating a blood vessel. Transmitting a Doppler signal with frequency F_t and receiving the backscattered signals from the red blood cells within the vessel at a frequency F_r

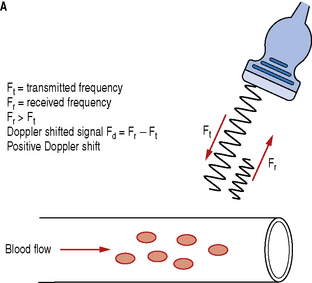
Let us consider a simple arrangement as seen in Figure 11.3. The transducer transmits a Doppler signal with frequency F_t. The transmitted Doppler signal interrogates a blood vessel and the transducer receives the backscattered signals from the red blood cells within the vessel at a frequency F_r. The Doppler frequency shift (F_d) can be calculated by subtracting the transmitted signal F_t from the received signal F_r.

Fig. 11.3 Demonstrating the resulting Doppler shifted signals for a) blood flow moving towards the transducer; b) blood flow moving away from the transducer

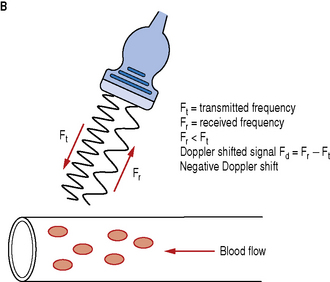
Blood flow moving towards the transducer produces positive Doppler shifted signals and conversely blood flow moving away from the transducer produces negative Doppler shifted signals. Figure 11.3 illustrates the change in the received backscattered signals and the resulting Doppler shifts for blood moving towards and away from the transducer.

In Figure 11.3a the relative direction of the blood flow with respect to the Doppler beam is towards the transducer. In this arrangement blood flow moving towards the transducer produces received signals (F_r) which have a higher frequency than the transmitted beam (F_t). The Doppler shifted signal (F_d) can be calculated by subtracting F_t from F_r and produces a positive Doppler shifted signal.

Conversely, Figure 11.3b illustrates blood flow which is moving away from the Doppler beam and the transducer. In this arrangement blood flow moving away from the transducer produces received signals (F_r) which have a lower frequency than the transmitted beam (F_t). This time the Doppler shifted frequencies (F_r − F_t) produces a negative Doppler shifted signal.

When there is no flow or movement detected then the transmitted frequency (F_t) is equal to the received frequency (F_r). Therefore F_r = F_t and F_d = F_r − F_t = 0, resulting in no Doppler shifted signals.

It is important to appreciate that the amplitude of the backscattered echoes from blood is much weaker than those from soft tissue and organ interfaces which are used to build up our B-mode anatomical images. The amplitude of the backscattered signal from blood can be smaller by a factor of between 100 and 1000. Therefore highly sensitive and sophisticated hardware and processing software is required to ensure that these signals can be detected and processed.

THE DOPPLER EQUATION

The Doppler equation shows the mathematical relationship between the detected Doppler shifted signal (F_d) and the blood flow velocity (V):

where:

F_d = Doppler shifted signal

F_t = transmitted Doppler frequency

c = the propagation speed of ultrasound in soft tissue (1540 ms⁻¹)

V = velocity of the moving blood

θ = the angle between the Doppler ultrasound beam and the direction of blood flow

The number 2 is a constant indicating that the Doppler beam must travel to the moving target and then back to the transducer.

Equation 1: The Doppler equation.

Relationship between Doppler Shifted Signal (F_d) and Blood Flow Velocity (V)

The Doppler equation (Equation 1) demonstrates that there is a relationship between the Doppler shifted signal (F_d) and the blood flow velocity (V). The Doppler shifted signal (F_d) is directly proportional to the blood flow velocity (V), which means greater flow velocities create larger Doppler shifted signals and conversely lower flow velocities generate smaller Doppler shifted signals. If we can detect and measure the value of F_d then the Doppler equation can be rearranged (see Equation 2) to calculate blood flow velocities (V) which can be processed and displayed.

Equation 2: Doppler equation rearranged to calculate blood flow velocities (V).

Significance of the Doppler Angle (θ)

Ultrasound machines are able to calculate Doppler shifted frequencies over a wide range of angles and it is important that an operator understands the significance of the angle of insonation (θ) between the Doppler beam and the direction of blood flow in vessels. Figure 11.4 graphically shows how the Doppler shifted signal changes as the Doppler beam angle changes.

Fig. 11.4 Graphically demonstrating the relationship between the Doppler shifted frequency with respect to the angle of the insonating Doppler beam

When the Doppler beam is pointing towards the direction of blood flow a positive Doppler shifted signal is observed, but once the Doppler beam is pointed away from the direction of blood flow a negative Doppler shifted signal is seen. The smaller the angle between the Doppler beam and blood vessel, the larger the Doppler shifted signal. Very small signals are produced as the Doppler beam angle approaches a 90° angle.

Table 11.1 shows the relationship between the angle of the Doppler beam (θ) and the value of cosθ. The value of cosθ varies with the angle from 0 to 1. When θ = 0°, cosθ = 1 and when θ = 90°, cosθ = 0.

Table 11.1 Variation of the value of cosθ over a range of angles of insonation. Maximum value of cosθ corresponds to a Doppler beam angle of 0°.

ANGLE θ	VALUE OF COSθ
0	1
30	0.87
45	0.71
60	0.5
75	0.26
90	0

For a constant flow velocity (V), the maximum value of cosθ and therefore the highest value of the Doppler shifted signal (F_d) is at an angle of 0°. This corresponds to a Doppler beam which is parallel with the vessel, which can rarely be achieved in practice.

Theoretically, when θ = 90° this means the blood flow is perpendicular to the Doppler beam, cosθ = 0 and no Doppler shifted signals will register.

In practice, when taking measurements of blood flow, a Doppler beam angle of between 30 and 60° is important to ensure reliable Doppler shifted signals. Avoid using angles greater than 60° and remember no Doppler shifted signals are generated at 90°.

Greater flow velocities and smaller angles produce larger Doppler shifted frequencies, but not stronger Doppler shift signals.

Typical Doppler Shifted Signals for Blood Flow

Ultrasound machines transmit high-frequency sound waves which lie in the megahertz range, typically between 2 MHz and 20 MHz. Substituting typical physiological blood flow velocities into the Doppler equation gives Doppler shifted signals which lie within the audible range. That is, the range of frequencies that the human ear can hear. A healthy young human can usually hear from 20 cycles per second to around 20 000 cycles per second (20 Hz to 20 kHz).

Let us calculate a typical Doppler signal frequency for blood moving at 0.5 ms⁻¹ which is illustrated in Figure 11.5. Transmitted frequency (F_t) is 4 MHz, θ = 60° and c (the propagation speed of ultrasound) is assumed constant at 1540 ms⁻¹.

Fig. 11.5 Illustrates the calculated Doppler shifted signal using the Doppler equation for blood flow moving at 50 cm/s for a Doppler beam operating at 4 MHz positioned with an insonation angle of 60°

Using the Doppler equation (Equation 1) we calculate the Doppler shifted frequency to be 1299 cycles per second, about 1300 Hz or abbreviated to 1.3 kHz.

These generated Doppler shifted signals can simply be converted into an audible signal which can be heard and monitored through a loudspeaker.

TYPES OF DOPPLER INSTRUMENTATION IN DIAGNOSTIC IMAGING

There are a number of types of Doppler instrumentation used in ultrasound which include:

• continuous wave Doppler

• color Doppler

• power Doppler

• spectral pulsed wave (PW) Doppler.

Doppler techniques applied to diagnostic ultrasound can be characterized as either being non-imaging or imaging. Non-imaging techniques typically use small or handheld units, and use continuous wave (CW) Doppler. The main purpose of these simple CW units is to either identify and/or monitor blood flow. Two examples of clinical examinations include fetal heart monitors in obstetrics and peripheral blood flow assessment in vascular practice.

Imaging Doppler techniques such as color and spectral PW Doppler are always used with B-mode imaging where the gray scale anatomical image is used to identify blood vessels and areas for blood flow evaluation. These techniques require more sophisticated processing than CW devices.

Continuous Wave Doppler Devices

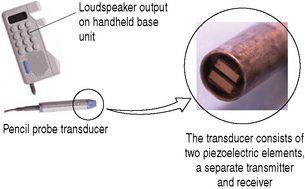
Continuous wave (CW) Doppler devices are the simplest of Doppler instruments and typically consist of a handheld unit with an integrated speaker which is connected to a pencil probe transducer (Fig. 11.6).

Fig. 11.6 A simple CW Doppler device illustrating the two piezoelectric elements at the tip of the pencil probe transducer: one acting as a continuous transmitter, the other acting as a continuous receiver

The transducer consists of two piezoelectric elements: one element acts as a continuous transmitter (F_t) and the other acts as a continuous receiver (F_r).

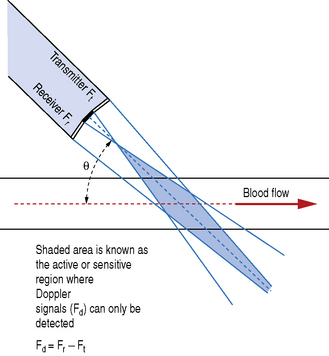
These two elements are set at an angle to each other so that the transmit and reception beams overlap one another, as illustrated in Figure 11.7. This crossover region is known as the active or sensitive area and is where Doppler signals can only be detected. Doppler shift signals (F_d) are detected by comparing the transmitted and received signals: F_d = F_r − F_t.