Abstract
Spinal cord functional imaging offers new insights into normal sensorimotor processing and monitoring disease processes affecting the cord. However, all imaging-based techniques suffer from unwanted contributions to the measured signal from nonneuronal physiological sources. Broadly, these noise sources can be grouped into those arising from cardiac or respiratory processes, as well as from their interaction. Different techniques for estimating and removing physiological noise, their implication for functional magnetic resonance imaging (fMRI) analysis, and their implementation within the framework of the general linear model will be demonstrated. Recommendations for preprocessing spinal fMRI data will be given, such as how to avoid potential inflation of recorded T-statistics and whether prewhitening is appropriate for processing spinal fMRI data. Finally, techniques for the registration of spinal cord functional imaging data to a standard spinal cord, for the purpose of group analysis, will be presented along with techniques for estimating significance from group data.
Keywords
Analysis, Functional magnetic resonance imaging (fMRI), General linear model, Physiological noise, Statistics
4.2.1
What is Physiological Noise?
Physiological noise can be defined as any signal change occurring in an image that is due to the subject and that is of no interest. Equally, movement of the subject (e.g., bulk movement of the cord) and indirect movement of structures of interest (e.g., caused by arterial pulsation or cerebrospinal fluid (CSF) flow) could also be included in this heading. For the purpose of this discussion, I will limit my attention to those signal changes arising from cardiac and respiratory processes, and how they influence the recorded signal on blood oxygenation level-dependent (BOLD)-based functional images, and not consider correction for bulk movement.
4.2.1.1
Where Does Physiological Noise Come from?
Krüger et al. proposed that physiological noise derives from processes that depend on cortical metabolism (e.g., cerebral blood flow, changes in PaCO 2 , cerebral blood volume, and consumption of oxygen) and physiological processes such as cardiac output and respiratory rate, which produce arterial pulsatility, drive CSF flow, and induce time-varying changes in the main magnetic field ( B 0 ). These processes are interdependent (e.g., chemoreceptors in the brainstem will record changes in the amount of CO 2 in the blood and, via sympathetic outflow, increase breathing rate). Equally, there is link between cardiac and respiratory function. An example of this is the connection between cardiac output (stroke volume) and the respiratory cycle, the so-called “respiratory pump” (increased cardiac output during inspiration). One implication of this coupling is that processes driven by cardiac pulsatility, such as CSF flow, will have a dependence on both the cardiac and respiratory cycles. This phenomenon has been investigated using magnetic resonance imaging (MRI) techniques in the brainstem and spinal cord, and it must be considered when attempting to account for sources of physiological noise in functional imaging experiments.
4.2.1.2
Why is Physiological Noise Important?
As described in Chapter 4.1 , the detection of task-related signals in functional MRI (fMRI) is assessed by statistical inference, and it is typically performed by using the general linear model (GLM), which can be expressed via the following equation:
Y = β · X + ε
Physiological noise may be the dominant source of noise in an fMRI experiment. Whilst raw signal to noise increases linearly with field strength, physiological noise increases with the square of the field strength, and as a consequence there is an asymptotic limit to the temporal signal-to-noise ratio (TSNR) that can be achieved at higher field strength. TSNR is the ratio of the mean signal intensity recorded from a time series of functional images, divided by the standard deviation of that signal. Hence, the best chance for detecting the small (∼1–2%) signal changes associated with functional activity will be in regions of high TSNR (i.e., where the baseline signal is high compared to its variance). In the theoretical model suggested by Krüger and Glover, two contributions to physiological noise were described: a component that induces changes via BOLD-like mechanisms (characterized by a constant c 1 , a relaxation rate R 2 ∗ , and the echo time (TE) of the experiment), and a non-BOLD component that depends only on a constant c 2 and the intrinsic signal intensity S . The relationship between these quantities, their dependence on field strength, and their impact on TSNR was further explored by Triantafyllou et al., as discussed in this chapter.
TSNR = SNR 0 1 + λ 2 · SNR 0 2 , where λ 2 = c 1 2 · Δ R 2 ∗ 2 · TE 2 + c 2 2
It is important to note that the influence of physiological noise depends not only on the intrinsic SNR 0 but also on the voxel size, with smaller voxels being less affected than larger ones (relative to the contribution from thermal noise). Equally, not all cortical or subcortical regions will be similarly affected by physiological noise. Krüger and Glover demonstrated distinct spatial patterns of physiological noise affecting brain images: it is increased in gray relative to white matter. Furthermore, when imaging more inferior (ventral) regions of the brain, around the thalamus, mesial temporal lobes, and brainstem, there is an increased contribution from the extrinsic (cardiac and respiratory) noise sources, due to the presence of large vessels (e.g., the Circle of Willis) and the closer proximity to the lungs.
When attempting to record functional signal from the spinal cord, one is faced with a great many challenges, not the least of which is the relative size of the structure of interest to the surrounding sources of physiological noise. The presence of relatively large spinal arteries and veins close to the surface of the cord (see Chapter 4.3 ) will contribute noise and potentially hinder the accurate localization of activity (see Chapter 4.1 ). Another significant source of noise arises from CSF in-flow effects in the subarachnoid space surrounding the cord, which will be prominent on single-shot image acquisitions using typical repetition times (TRs ≤3 s) and flip angles close to the Ernst angle (∼80°). Left unaccounted for, the various sources of physiological noise each contribute to the measured signal in the fMRI experiment and will reduce the TSNR, placing strict demands on the experimental paradigm (i.e., an increased signal averaging and an increased number of stimuli). When combined with intrinsically low raw signal to noise (due to receive coil coverage and the need for relatively small voxel volumes), it is apparent that physiological noise may be the “dominant” signal in spinal FMRI experiments.
4.2.1.3
The Noise Characteristics of fMRI Data
In an early study, the power spectrum of resting fMRI data from the brain was shown to have significant power at low frequencies; this is generally referred to as “1/ f -like” noise (i.e., increased power at low frequencies). The presence of low-frequency noise has implications for analyzing fMRI data as the statistical models that are typically used assume that each sample of activity (i.e., each volume) is independent of other measurements in the experiment, and that the noise is equally distributed across the frequency range sampled. Clearly in the case of fMRI data, the observation of increased power at low frequencies would invalidate this assumption, as the noise is not equally represented at all frequencies. Another characteristic of fMRI data is that they are temporally autocorrelated, which put simplistically means that preceding data points can predict subsequent data–invalidating the assumption of independence. The low-frequency energy in the spectrum of fMRI time-series data and temporal autocorrelation are thought to be due to the presence of physiological noise and synchronized low-frequency neuronal activity across widespread brain regions. Several techniques for assessing and correcting for temporal autocorrelation exist, and their importance for spinal fMRI data will be discussed in this chapter.
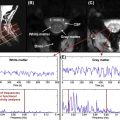
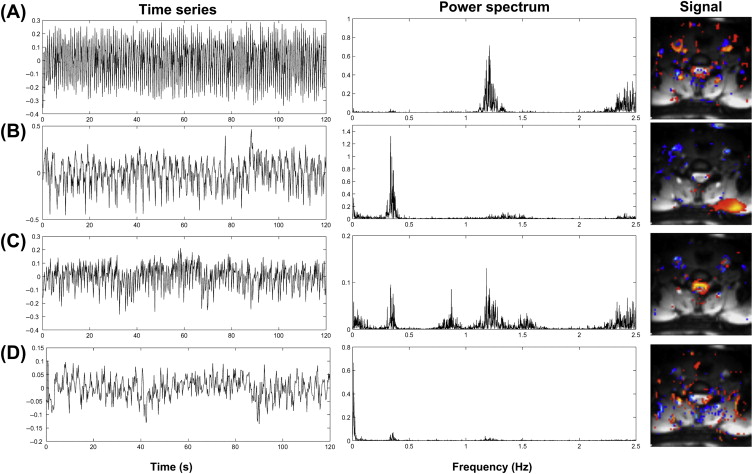
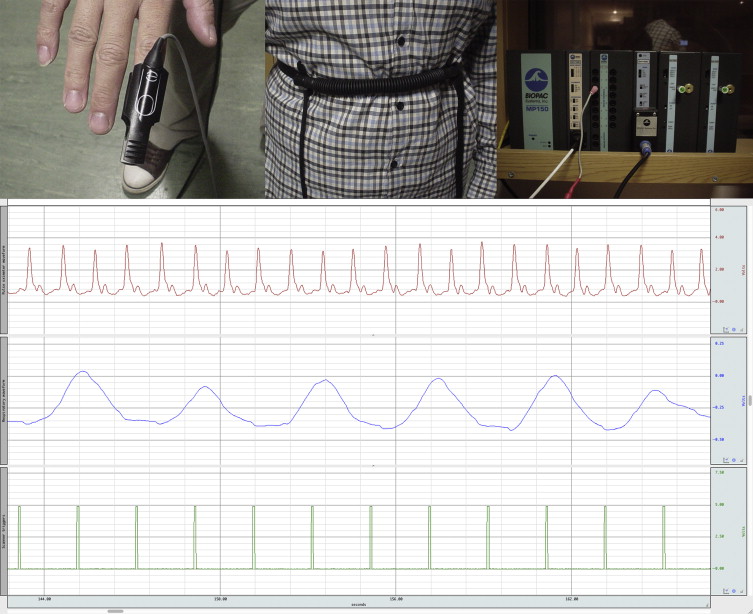
Brooks et al. investigated the presence of physiological noise in single-shot echo-planar imaging (EPI) data acquired from the human spinal cord with a short TR (200 ms) and no task (i.e., a resting experiment), by using an explorative technique based on independent component analysis. These data revealed structured signals that were spatially and temporally distinct, and they had characteristic frequencies indicating that they derived from cardiac (around 1 Hz) and respiratory (around 0.3 Hz) processes. A component arising due to the interaction between cardiac and respiratory processes, and very low-frequency signals in the CSF surrounding the cord ( Figure 4.2.1 ), were also observed.
4.2.2
Time Domain Filtering
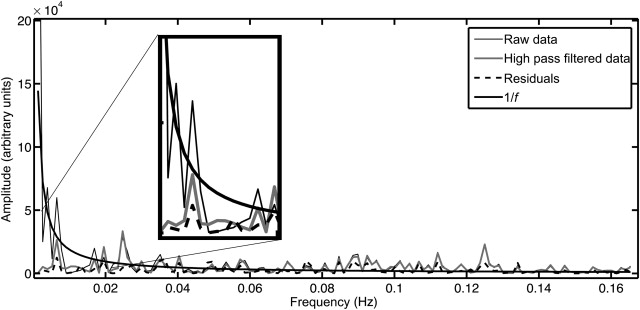
Temporal filtering is frequently applied during preprocessing of fMRI data, and it aims to remove signals from the data that are unrelated to the experiment (e.g., low-frequency drift due to scanner hardware considerations, or high-frequency signals arising from physiological processes). Two methods that are typically applied are high-pass filtering (HPF) and low-pass filtering (LPF), or a combination of the two: band-pass filtering (BPF). The first of these, high-pass filtering, can be achieved by applying a filter to the time-series data prior to estimation with the GLM or by including low-frequency cosine waveforms in the GLM—a linear combination of which will account for low-frequency signals in fMRI data ( Figure 4.2.2 ). Almost all fMRI analysis packages will use an HPF as it will generally improve the obtained estimates for the parameters of interest by removing slow drifts from the fMRI time series that would otherwise remain as unmodeled variance in the data (increasing the variance of the residuals).
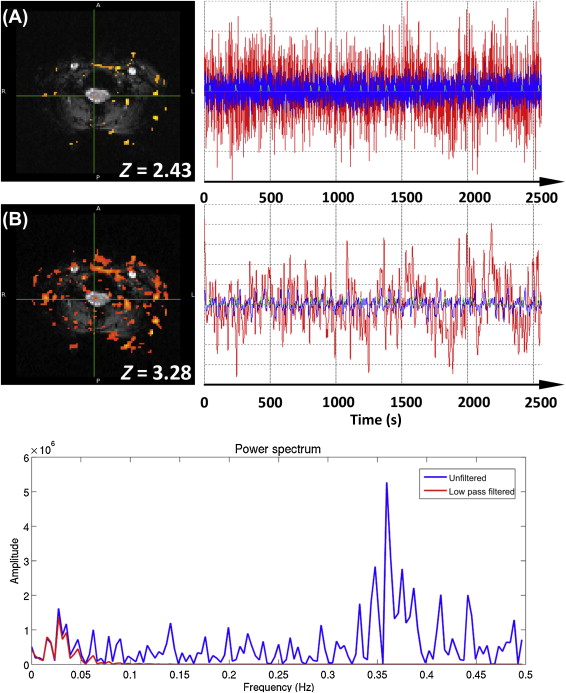
The second type of filter, the LPF, aims to remove high-frequency signals from the data, leaving the lower frequencies of typical fMRI designs unaffected. While the use of an LPF might seem an intuitive approach to removing physiological signals that are of higher frequency than the experimental paradigm, there are two significant problems with its application: (1) physiological signals are typically undersampled due to the relatively long TR (e.g., 3–5 s) used in fMRI experiments (i.e., they are not “critically sampled”) and thus may be aliased to low frequencies overlapping with the experimental paradigm; and (2) an LPF increases the smoothness of the time-series data, which has the effect of reducing the independence of time points, effectively reducing the number of independent samples in the data set. If the reduction of degrees of freedom is not accounted for in the applied statistical modeling, this will lead to artificially inflated t- and Z-scores, and it is illustrated and described in Figure 4.2.3 .
4.2.3
Approaches for Reducing the Effects of Physiological Noise
Several techniques for minimizing the effect of physiological noise have been described, and they can be divided into three broad groups: (1) those that rely on the independent measurement of some physiological parameter (e.g., cardiac waveform or chest wall position), (2) those that require additional image acquisitions to measure the impact of physiological noise and then remove them from the experimental data, and (3) those that alter the data acquisition to attempt to minimize artifacts due to physiological processes.
4.2.3.1
External Physiological Measurements
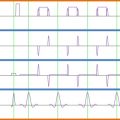
One approach to taking account of the presence of physiological signals in an FMRI time series is to make a direct measurement of the subject’s physiology, and then attempt to remove the corresponding signal from the data. Typically, the biological processes that one is most interested in are the cardiac and respiratory cycles, although other physiological parameters might also be of interest, such as galvanic skin response (GSR), pupil diameter (measured with an eye-tracking apparatus), noninvasive blood pressure, end-tidal CO 2 , and arterial blood flow (measured with transcranial Doppler sonography). Considering the simplest case of cardiac and respiratory data, the relevant waveforms can be obtained via photoplethysmography (pulse oximetry) or electrocardiogram (ECG) leads, and pneumatic respiratory bellows, respectively. These data normally would be acquired using a commercial physiological monitoring unit, and the results recorded in real time via an analog-to-digital convertor attached to a personal computer. A typical setup is shown in Figure 4.2.4 .
4.2.3.1.1
Data Logging
An important requirement of the independent measurement techniques is that the physiological waveforms should be recorded alongside the timing of the image acquisition, and this is typically achieved by recording “scanner” or “volume” triggers (or transistor–transistor logic (TTL) pulses) on the same computer used to log the physiological traces. The various traces can be seen in Figure 4.2.4 , which in this case were sampled at a rate of 100 Hz—which is sufficient to accurately represent these waveforms. In practice, when recording electrophysiological signals such as ECG or electromyogram (EMG), the sampling rate is normally higher to enable artifacts induced by gradient switching to be filtered from the traces. It should be noted that in the case of some waveforms, the absolute magnitude of the recorded signal may be important (e.g., chest wall position measured via respiratory bellows), and this may place limits on the monitoring apparatus to be used. For example, the physiological signals recorded by the scanner’s own monitoring equipment may be arbitrarily scaled for display purposes, making them unsuitable for subsequent physiological signal estimation.
4.2.3.1.2
Do I Need to Buy a Dedicated Physiological Recording System?
In most scanners, it is possible to obtain the trace of the physiological signal that is meant to be used for gating (e.g., respiratory trace or pulse oximetry). However, it may not be straightforward to then synchronize these traces to the actual timing of the data, or in some cases the physiological traces are not appropriately sampled. For example, in some scanners, the internal clock used for sampling the signal may not be the same as the one used for timing the image acquisition; as a result, a temporal drift may appear between the two signals (the physiological signal and data acquisition signal), making the physiological traces useless for physiological noise correction. Custom setups can provide a workaround (e.g., output the volume trigger from the scanner given at each TR, and input it into the internal physiological monitoring system of the scanner). In conclusion, it may be easier to buy an external device for monitoring physiological traces, and such a device may also offer other possibilities (e.g., end-tidal CO 2 and skin conductivity measurements).
4.2.3.1.3
Defining the “Phase”
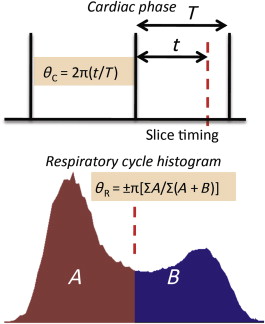
Most of the techniques discussed in this chapter rely on the definition of cardiac or respiratory phase. In this context, “phase” refers to some measure of position within the cardiac or respiratory cycle, and it is illustrated here. The cardiac phase is relatively straightforward to measure, as it can be defined as the time of an event (say, acquisition of an imaging slice) relative to the preceding cardiac event (the R-wave or peak in pulse oximetry tracing), divided by the time interval between the surrounding cardiac events. The respiratory phase depends on both the timing of the slice acquisition relative to the respiratory events—from the start of inspiration (inhalation) to the end of expiration (exhalation)—and the depth of breathing. In other words, the effect of lung volume (or chest wall position) on the static magnetic field ( B 0 ) when taking small breaths is not equivalent to that produced when breathing deeply. So the respiratory phase cannot be assigned by simply recording the respiratory trace and working out the slice timing relative to the detected peaks. One way to correctly assign respiratory phase is to construct a histogram of all bellows recordings taken during an experiment, then the phase may be calculated by summing up all of the bellows recordings up to the value recorded at the time of interest (e.g., the acquisition time of a given slice), and then dividing by the sum of all histogram values (see Figure 4.2.5 ). The resulting fraction of the total histogram area defines a phase between 0 and π, and the sign of the phase depends on whether, at the time of the slice acquisition, the subject was inhaling (positive sign) or exhaling (negative sign). Note that, in general, phase is represented as a value between 0 and 2π, or −π and +π, which can then be used to indicate how far along the periodic process you are.
4.2.3.1.4
k -Space-Based Techniques
In an early report, Hu et al. proposed a method for removing quasiperiodic physiological signals from time-series fMRI data by using a low-order Fourier expansion and the recorded k -space data. As mentioned in earlier chapters, k -space refers to the raw time-domain signal that is recorded by the scanner and subsequently converted into images via the two-dimensional (2D) Fourier transform. For each point in k -space, the timing of the slice acquisition is used to calculate a phase, which is then fed into a Fourier expansion (as discussed in this chapter) to model the effect of the physiological signals ( y phys ( t )) present in the data:
y phys ( t ) = ∑ n = 1 N a n ca sin ( n θ ca ) + b n ca cos ( n θ ca ) + a n re sin ( n θ re ) + b n re cos ( n θ re )
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree