Renal masses increasingly are found incidentally, largely due to the frequent use of medical imaging. Computed tomography (CT) and MR imaging are mainstays for renal mass characterization, presurgical planning of renal tumors, and surveillance after surgery or systemic therapy for advanced renal cell carcinomas. CT protocols should be tailored to different clinical indications, balancing diagnostic accuracy and radiation exposure. MR imaging protocols should take advantage of the improved soft tissue contrast for renal tumor diagnosis and staging. Optimized imaging protocols enable analysis of imaging features that help narrow the differential diagnoses and guide management in patients with renal masses.
Key points
- •
Computed tomography (CT) protocols for renal mass evaluation should be tailored to the clinical indications with careful considerations of balancing diagnostic accuracy and radiation dose.
- •
MR imaging serves as a problem-solving tool in renal mass evaluation, and MR imaging protocols should take advantage of its multiparametric capability to provide additional information for renal mass characterization.
- •
Optimized CT and MR imaging protocols enable analysis of imaging features that help narrow the differential diagnoses and guide management in patients with renal masses.
Introduction
Renal masses increasingly are found incidentally during work-up for nonrenal indications, largely due to the frequent use of medical imaging. These include renal cysts, benign renal tumors, and renal cell carcinomas (RCCs) that have variable biological aggressiveness. Imaging is essential in renal mass characterization in order to guide appropriate treatment selections, because the management paradigm of localized renal tumors has evolved in recent years to include active surveillance and thermal ablation in addition to partial and radical nephrectomy. Furthermore, imaging plays a key role in the presurgical planning of renal tumors and in surveillance after surgery or systemic therapy for advanced RCCs.
Computed tomography (CT) and MR imaging with intravenous (IV) contrast are the mainstays of renal mass evaluation. This review focuses on the CT and MR imaging protocol selection and optimization for renal mass evaluation. Contrast-enhanced ultrasound with microbubble agents is a useful alternative for characterizing renal masses, especially for patients in whom iodinated CT contrast or gadolinium-based MR imaging contrast is contraindicated. Contrast-enhanced ultrasound is discussed in detail in a separate chapter.
Computed tomography
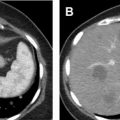
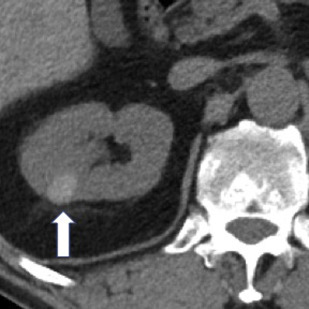
CT is the most commonly used modality for the detection and characterization of renal masses as well as presurgical planning and post-therapy surveillance. Renal masses usually are discovered incidentally on either a non–contrast-enhanced or a single-phase postcontrast CT obtained for unrelated indications. Some masses can be confidently characterized on these images without requiring a subsequent dedicated multiphase renal protocol CT or MR image. For example, renal masses that are homogeneous and have Hounsfield units (HU) measuring fluid density (between −10 HU and 20 HU) on non–contrast-enhanced CT are benign simple cysts. Those that are homogeneous with HU greater than 70 are hemorrhagic or proteinaceous cysts ( Fig. 1 ) 99% of the time. For these masses, no further imaging is indicated. Similarly, on a single-phase postcontrast CT, renal masses that are homogeneous and measure fluid density are simple cysts. Recent data also suggest that well-defined homogeneous renal mass with attenuation 30 HU or less on the portal venous phase CT can be considered benign cysts and require no additional imaging. , When the initial CT is unable to provide a definitive diagnosis, subsequent multiphase renal protocol CT after IV contrast injection commonly is obtained for further characterization of a renal mass.
Multiphase Renal Protocol Computed Tomography
When further work-up for a renal mass is deemed necessary, additional imaging can be obtained using a multiphase renal protocol CT. Enhancement patterns across different phases after IV contrast injection can be used to distinguish renal cysts from solid tumors and may aid in subtyping of renal tumors.
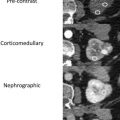
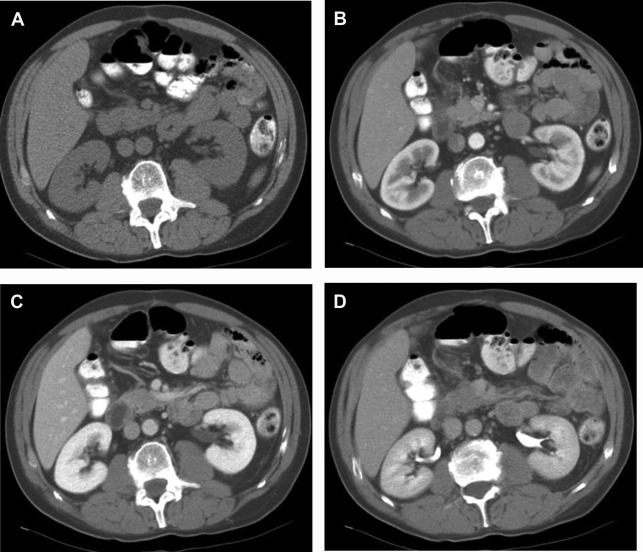
Although the specifics of a renal protocol CT vary by institutions, the following phases in their various combinations commonly are used: precontrast phase, corticomedullary phase, nephrographic phase, and excretory phase ( Fig. 2 A–D). The combination of these phases may be modified depending on the clinical indications, such as for initial lesion characterization, surgical or ablation planning, or post-treatment follow-up. The field of view, whether restricted to the kidneys themselves or expanded to include from the diaphragm to the iliac crest, also depends on the clinical questions.
Precontrast Phase
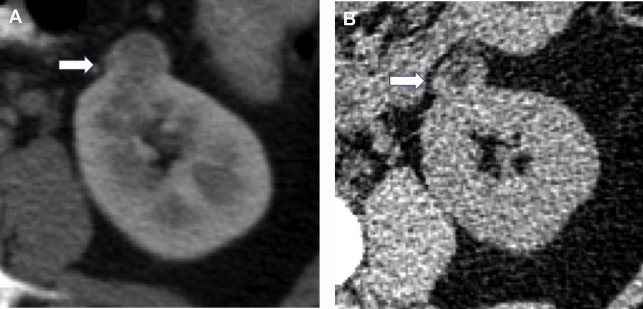
Precontrast CT provides better detection of small amounts of intralesional fat compared with postcontrast CT ( Fig. 3 ). In order to optimally visualize the small foci of fat, thin sections (eg, 1.25 mm) may be required. Similarly, precontrast CT also improves visualization of calcification ( Fig. 4 ) compared with postcontrast CT or MR imaging. Angiomyolipomas (AMLs) can be diagnosed confidently once intralesional macroscopic fat has been identified in the absence of other worrisome findings, such as intralesional calcification. On the other hand, the presence of intralesional calcification, regardless of the presence of fat, should prompt suspicion for malignancy, such as RCC.
Corticomedullary Phase
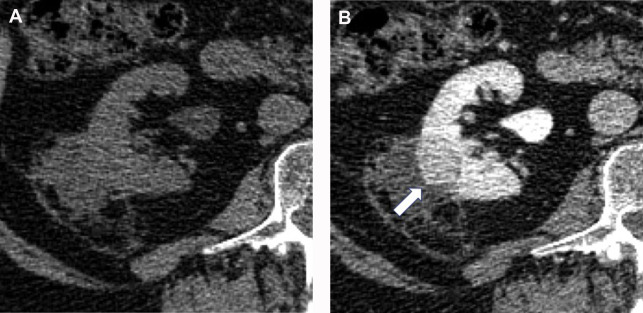
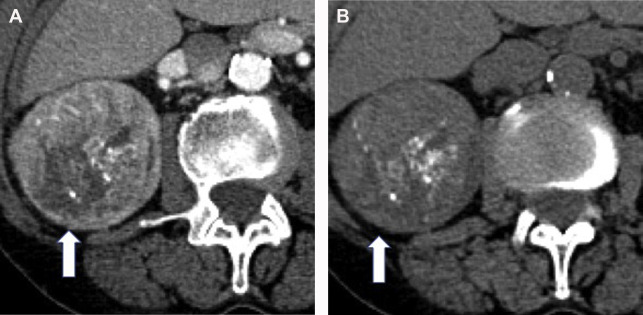
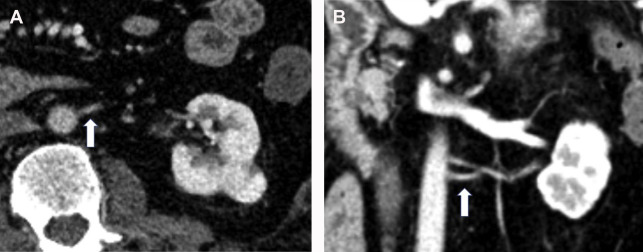
Corticomedullary phase typically is acquired 40 seconds to 70 seconds after IV contrast injection (see Fig. 2 B). During this phase, there is intense enhancement of the renal cortex, allowing differentiation between the cortex and the medulla. This phase is useful in confirming anatomic variants, such as column of Bertin, which can mimic a tumor but which has the same corticomedullary differentiation as normal kidney parenchyma ( Fig. 5 ). The renal vasculature also enhances intensely in this phase, which can provide additional information for surgical planning if needed ( Fig. 6 ) or identify vascular anomalies, such as pseudoaneurysm and arteriovenous fistula.
Nephrographic Phase
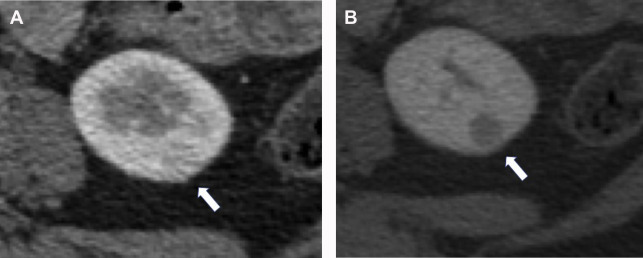
Nephrographic phase is the most sensitive for detecting renal lesions. Obtained at 100 seconds to 120 seconds after IV contrast injection, the timing for this contrast-enhancement phase is later than the typical portal venous phase, allowing for uniform enhancement of the renal parenchyma and in general providing the highest tumor to background distinction compared with the other phases ( Fig. 7 ). It has been reported that up to 66% more small renal masses are detected in the nephrographic phase compared with the corticomedullary phase. Nephrographic phase also may improve the assessment of enhancement in poorly vascular tumors. For example, papillary RCCs typically demonstrate low-level progressive enhancement, peaking at the nephrographic phase ( Fig. 8 ); therefore, tumor contrast enhancement is more conspicuous on the nephrographic phase compared with the earlier corticomedullary phase. Measurement of HU change after contrast administration using the earlier corticomedullary phase in a papillary RCC may result in erroneous categorization of the lesion as a nonenhancing cyst (see Fig. 8 ). In the setting of advanced RCCs, tumor extension into the renal vain or inferior vena cava may be best assessed on the nephrographic phase as well.
Excretory Phase
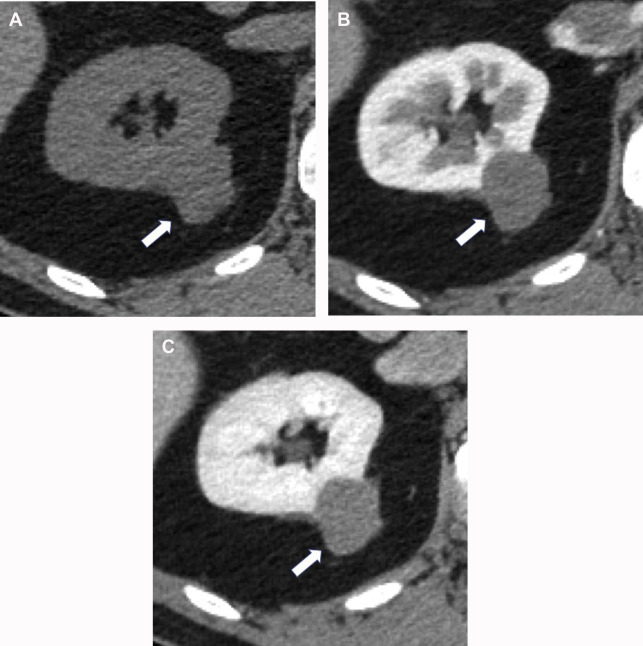
Excretory phase is obtained at 7 minutes to 10 minutes after IV contrast injection. Contrast material is excreted into the renal collection system, ureters, and bladder in this phase, allowing better visualization of these structures. This phase is helpful for identifying RCC involvement of the collecting system as well as diagnosing primary malignancy arising from the collecting system, such as urothelial carcinoma involving the kidney ( Fig. 9 ).
Society of Abdominal Radiology Suggested Protocols
The Society of Abdominal Radiology (SAR) Disease-Focused Panel (DFP) on RCC is a multi-institutional working group aimed at addressing the unmet needs in the clinical care, research, and education in RCCs. The group has suggested standardized CT protocols for renal mass evaluation based on different clinical indications, as described later. The suggested imaging protocols are based on expert consensus, with the goal of balancing diagnostic efficacy and radiation exposure ( Table 1 ).
| Indications | Contrast Phases | Field of View | Timing | Comment | |
|---|---|---|---|---|---|
| Indeterminate renal mass | Recommended scan series | Precontrast | Kidneys only | ||
| Nephrographic | Kidneys only | 100–120 s delay | |||
| Optional additional scan series | Corticomedullary | Kidneys only | 40–70 s delay | May be helpful in subtyping RCC | |
| Excretory | Diaphragm to iliac crests | 7–10 min delay | May be helpful to differentiate urothelial cancer from RCC and parapelvic or peripelvic cysts from hydronephrosis and to diagnose calyceal diverticula | ||
| Pre–partial nephrectomy or preablation planning for renal masses that have been previously completely characterized | Recommended scan series | Arterial | Kidneys only | 30 s delay | Better depict the arteries and their relationship to the renal mass |
| Nephrographic | Diaphragm to iliac crests | 100–120 s delay | |||
| Excretory | Diaphragm to iliac crests | 7–10 min delay | Better depict the relationship between the collecting system and the mass. | ||
| Active surveillance; postablation surveillance; post–partial nephrectomy surveillance | Recommended scan series | Precontrast | Kidneys only | May be omitted for active surveillance if the primary goal is to determine renal mass size change | |
| Nephrographic | Diaphragm to iliac crests | 100–120 s delay | |||
| Optional additional scan series | Excretory | Diaphragm to iliac crests | 7–10 min delay | May be helpful after ablation or partial nephrectomy when collecting system injury is suspected | |
| Post–radical nephrectomy surveillance; systemic therapy surveillance | Recommended scan series | Portal venous | Diaphragm to iliac crests | 60–90 s delay | |
| Optional additional scan series | Late arterial | Diaphragm to iliac crests | 40–50 s delay | Can be included in patients at high risk of metastatic disease to improve detection of liver and pancreatic metastases |
IV contrast generally is needed for the characterization, staging, surveillance, and post-treatment follow-up of renal tumors. , Suggested IV contrast type by the SAR DFP is low-osmolar or iso-osmolar contrast material, at a dose of 35 g to 52.5 g iodine equivalent (ie, for contrast material that contains 350 mg of iodine/mL, the corresponding dose is 100–150 mL), or weight-based dosing. The injection rate is suggested at 2 mL/s to 5 mL/s.
CT images are acquired in the axial plane, with suggested 3-mm reconstruction section thickness. Multiplanar reformats in the coronal and sagittal planes of each postcontrast scan series also can be done with 3-mm reconstruction section thickness without overlap.
Suggested Protocol for Evaluation of Indeterminate Renal Masses
For indeterminate renal masses, the field of view can be restricted to the kidneys only, with precontrast and nephrographic (obtained at 100-second to 120-second delay) phases considered essential for this indication. These 2 phases allow the differentiation between solid and cystic renal masses.
Corticomedullary and excretory phases may be acquired optionally. The excretory phase may be helpful for distinguishing urothelial cancers from RCCs and parapelvic or peripelvic cysts from hydronephrosis and for diagnosing calyceal diverticula. The corticomedullary and excretory phases together with the precontrast-phase and nephrographic-phase images may be helpful to subtype renal masses. , For example, prior studies have shown that clear cell–type RCCs demonstrate peak enhancement during the corticomedullary phase. In contrast, papillary RCCs demonstrate greater enhancement at later phases. By applying enhancement thresholds, 1 study has shown that 4-phase CT attenuation profiles enabled differentiation of clear cell RCCs from other solid renal cortical masses, notably from papillary RCCs and lipid-poor AMLs. Such information can be helpful in guiding patient management. For example, a tumor with enhancement features that suggest a papillary RCC can be confirmed with percutaneous biopsy. Given the indolent nature of papillary RCCs in general, these may be appropriate for active surveillance rather than surgical resection, especially in patients who are poor surgical candidates. , Although multiphase CT for tumor subtyping is promising, there are no prospective studies to date that have validated the reported enhancement threshold.
Suggested Protocol for Pre–Partial Nephrectomy or Preablation Planning of Renal Masses that Have Been Previously Completely Characterized
For pre–partial nephrectomy or preablation planning of renal masses that have been previously completely characterized, the primary goal is to delineate the tumor and vascular anatomy. Arterial phase (approximately 30-second delay) with field of view focused on the kidneys is recommended to better depict arteries and their relationship to the renal tumor. Nephrographic and excretory phases also are included, with the field of view expanded from diaphragm to iliac crest. The excretory phase allows better depiction of the relationship between the mass and the renal collecting system.
Suggested Protocol for Active Surveillance, Postablation Surveillance, Post–Partial Nephrectomy Surveillance
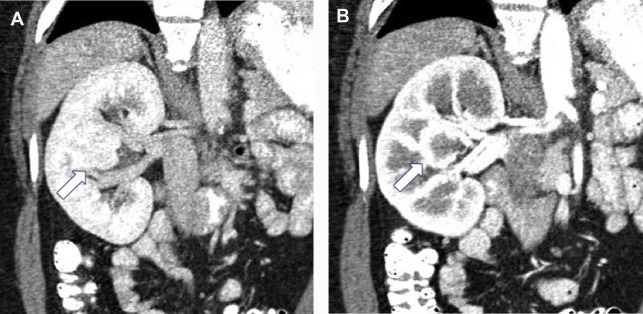
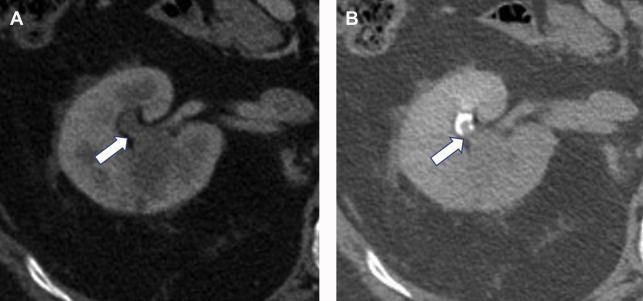
For active surveillance, postablation surveillance, or post–partial nephrectomy surveillance, precontrast and nephrographic phases should be obtained. The precontrast and nephrographic phase images are used to evaluate for changes of tumor size or enhancement characteristics in cases of active surveillance or detecting enhancing tumor in post-treatment settings ( Fig. 10 ).