Radiation Therapy with Protons and Heavy Ions

(9.1)where K = 0.307075 MeV cm² g⁻¹, z is the charge of the projectile ion, Z/A is the average ratio of the atomic number over the atomic mass of the medium, W _max is the maximum energy that the ion can transfer to an electron in a single collision, I is the mean excitation energy of the medium, and corr summarizes various corrections (density effect, shell, Barkas and Bloch corrections) which are especially important at very high and low energies. The most important dependence on the projectile is via the charge and velocity: the β ⁻²term leads to a strong increase of energy loss at low energies. This behavior gives rise to a steep increase of the depth dose curve, the so-called Bragg curve. After the Bragg maximum, the energy loss drops rapidly, when the particles have lost all their energy and are stopped. This feature can be seen in the depth dose curve of various particles as compared to X-rays in Fig. 9.1.

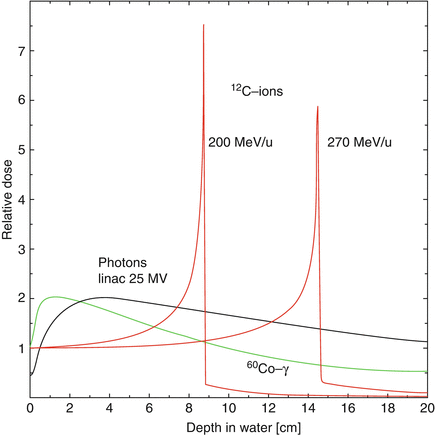
Fig. 9.1

Depth dose curves for ⁶⁰Co gamma radiation, MV photons, and carbon ions at different energies in water (Reproduced from Ref. [29])

The range can be calculated by the continuously slowing down approximation (csda) by integrating the inverse of the stopping power over the energy of the particle:

${R}_{\mathrm{csda}}=\underset{E_0}{\overset{0}{{\displaystyle \int }}}{S}_{\mathrm{coll}}\cdot \mathrm{d}E$

(9.2)

The difference between protons and heavier ions arises primarily through the z ²-term: the higher charge leads to much increased energy loss; in case of carbon ions as compared to protons, this factor is 36:1. At the same range, the difference is somewhat smaller due to a larger β of carbon as compare to protons. For carbons with a range of 15 cm, the energy loss is about 25 times that of protons with the same range. The Bethe formula is therefore the direct reason why higher energies are needed for carbon ion therapy as compared to proton RT, resulting in larger machines and considerably more expensive facilities.

To understand the importance of a higher energy loss, it is important to realize, where this energy is deposited in tissue. Generally the energy transferred to the atomic electrons during collision with protons and ions is very small: the maximum energy that can be transferred is around 1 MeV, but the average energy loss is only around 1 keV. This is due to the very asymmetric energy loss distribution, the so-called Landau distribution, which describes the probability of the energy loss with a certain value (the Bethe formula, only calculates the average energy loss of many ions). Since these values change only slightly for various ions and energies, the energy lost by an ion is generally transferred into a very small region, with a diameter of only nanometer scale. This is in contrast to MV photons, where energy can be transported away up to several millimeters or even centimeters.

This difference in energy loss patterns is attributed to the linear energy transfer, or LET, defined as the restricted energy loss. The restriction is done by limiting the maximum energy of secondary electrons which are produced in a collision, i.e., by replacing W _max in Eq. 9.1 by a cutoff value ΔE. Since the maximum energy transfer in ion beams is anyway small, LET is effectively equivalent to dE/dx in most practical cases. Consequently carbon ions are considered high LET radiation, protons are intermediate, and MV photons are low LET radiation. The higher LET is connected to an increase in biological effectiveness and other specific biological properties (see below).

Two more features of heavier ions are also important for radiotherapy: due to nuclear interactions between projectile and target nuclei, a considerable part of the ions undergo fragmentation reactions. This leads to the buildup of a secondary particle spectrum, consisting mainly of projectile fragments with energies similar to the energy of the incoming ion. Target fragments are less important, due to the relatively low energy transferred by the recoil and the resulting very small ranges. Secondary ions with lower charge but similar velocity as the primary have longer range due to lower energy loss (see Eq. 9.1). This leads to a pronounced tail of light particles beyond the Bragg peak of the primaries as seen in Fig. 9.1.

Besides the secondary ions, there will also be neutrons and gamma rays, which are emitted by de-excitation of nuclei after the collision. Some of this secondary radiation can be used for in vivo monitoring of the irradiation. Likewise some nuclei will be transformed into radioactive isotopes emitting positrons so that also positron emission tomography can be used for a 3D reconstruction of the irradiated volume.

Moreover, nuclear fragmentation leads to a significant loss of primaries with approximately 4 % per cm, i.e., at a depth of 15 cm, nearly half of the primaries are lost. Nevertheless, the energy loss is dominated by carbon ions, due to their significantly higher energy loss according to the Bethe formula.

As the loss of primaries is increasing with increasing atomic number of the projectile, ions which are considerably heavier than carbon are not suitable for radiotherapy. For example, for argon, only 22 % reach a Bragg peak in a depth of 20 cm [27]. This leads to an energy loss which is considerably higher at the entrance than at the Bragg peak.

Finally the increased mass of heavier ions as compared to protons leads to a significant reduction of the lateral penumbra of treatment beams. The reason for this is the smaller deflection of a single ion due to its higher momentum as compared to protons. A single scattering process is described by the differential Rutherford scattering cross section, which describes the cross section as a function of the solid angle Ω, the energy of the projectile E, and the charges of projectile and target nuclei, Z ₁and Z ₂:

$\frac{ds}{dW}\propto \frac{Z_1^2{Z}_2^2}{E^2}\cdot \frac{1}{{ \sin}^4\frac{\varTheta }{2}}$

(9.3)

As the probability for large-angle scattering is decreasing rapidly, this leads to the phenomenon of small scattering angles. The process of multiple small scattering events during traversal of thicker layers is described by multiple scattering theories, like the Moliere theory [37]. The dependency on the energy leads to a strong decrease of scattering angles with mass of the projectile. This again is the rationale for the interest in using helium ions, which offer considerable improved lateral penumbra as compared to protons but only a moderate increase of LET and also costs (see [36] for a detailed comparison of carbon ions and protons for radiotherapy).

In Fig. 9.2 an example of the development of the penumbra of various ions is given as a function of depth in water.

Fig. 9.2

Beam width of proton, helium, and carbon ion beams, expressed as full width half maximum as a function of depth in water. An initial width of 4 mm is assumed (Courtesy of U. Weber)

9.3 Biological Characteristics of Heavy Charged Particles

Generally, the dose needed to produce a certain biological effect using radiation with a higher LET is lower as compared to photon radiation [19]. This is due to the abovementioned deposition of large amounts of energy into very small volumes around the track. High LET radiation is thus referred to as densely ionizing. Since most clinical experience on biological effectiveness of radiation available is for MV X-rays, a concept for transferring these data high LET radiation is needed. Such a concept is the relative biological efficiency (RBE), which is defined as:

$\mathrm{R}\mathrm{B}\mathrm{E}=\frac{D_{\mathrm{photon}}}{D_{\mathrm{ion}}}.$

(9.4)

Here, D_photon and D_ion are the absorbed doses for photons and ion radiation, leading to the same biological effect. The RBE-weighted dose of ion irradiation is used to quantify the dose, which is isoeffective to a photon dose, given as the product of the absorbed dose multiplied by RBE.

Despite the simple definition in Eq. (9.4), RBE is a complex quantity since it depends on LET, dose, particle type, and energy, on the biological system (tissue type) as well as on the biological endpoint (e.g., early vs. late effects). For treatment planning applications, it is generally not possible to model all these dependencies explicitly and approximations have to be made.

There are currently no RBE data derived directly from clinical data of proton or ion beam therapy. Instead models are used, which describe some of the most important dependencies of RBE.

The nature of high LET radiation implies some important differences as compared to the biological effects of X-ray: while the average spacing between energy transfer events along the track is of the order of hundreds of nanometers for low LET, high LET radiation with an LET of 100 keV/μm leads to a mean spacing between events of less than a nanometer. This leads to interaction between ionization events in a single track and results in a higher probability of irreparable damage even from a single track, so-called cluster damage. With increasing LET, the effectiveness will therefore increase until it saturates. For higher LET, RBE will decrease as the effectiveness is constant and the deposited dose increases further with LET. This decrease of RBE at very high LET values is called overkill effect and appears around 100–200 keV/μm as seen in a compilation of RBE data in Fig. 9.3 [33] for different cell lines and ions.

Fig. 9.3

Compilation of RBE data for various ions and cell types (Data from Ref. [33], image reproduced from [23])

For different ions, the RBE as a function of LET is different, with the position of the maximum appearing at higher LET values for particles with higher charge. This is due to the fact that at same LET, lighter particles have lower energy and a smaller track radius, leading to higher energy density in the track as compared to heavier particles.

In addition there is a dose dependency of RBE, which is important when the dose per fraction is changed. The RBE for hypo-fractionated treatments is generally smaller than for more conventional fractionation schemes, with the strength of this dependency being determined by the α/β values of the tissue involved.

The dose dependence of RBE for ions can easily be explained by looking at the cell survival curves (Fig. 9.4): while photon survival curves exhibit the well-known, shoulder, survival curves for ions are getting more and more linear with increasing LET. Due to the nonlinearity of the photon survival curve, the ratio of doses to achieve the same survival level for both radiations is increasing for lower doses. In the very low dose region, the behavior of RBE may be different due to deviations of the survival curve from a purely linear-quadratic form.

Fig. 9.4

Cell survival curves for photons and ions and determination of RBE for cell inactivation at 10 % and 1 % survival level (Image reproduced from Ref. [29])

Consequently, the ratio of RBE in normal tissues vs. tumor tissue has to be carefully considered, in order to select a fractionation scheme which leads to therapeutic gain, as crossing of RBE values as function of dose my occur (see Fig. 9.5).

Fig. 9.5

Dose dependence of RBE for three different tissue characteristics as predicted by the simple linear-quadratic approach. Image reproduced from Ref. [8]

When looking at the dependence of RBE on dose, it can be seen that tissues with higher α/β ratio (typically cells with lower repair capacity) exhibit a slower variation with dose as compared to cells with lower α/β ratio (typically cells with higher repair capacity and hence higher radiation resistance). This behavior demonstrates an additional biological benefit, when tumors with low α/β are treated within a tissue of higher α/β at conventional fraction doses around 2Gy. Since the knowledge of α/β ratios especially for tumors is limited, estimates for the values used in treatment planning have to be made carefully (see Ref. [18]). Moreover the RBE may be different for early and late reactions.

Finally there is evidence from in vitro data that the microenvironment of tumor cells is less important for the cell survival in high LET than in low LET radiation. The most important effect may be the oxygen enhancement ratio, which describes a decrease of radiation sensitivity of cells which are poorly oxygenated. This effect is decreasing at higher LET, where no difference can be observed (see Fig. 9.6). This behavior might be highly beneficial in hypoxic tumors, which are difficult to control with conventional radiation. In order to obtain a significant OER effect, it may be necessary to use ions, like oxygen, which provide even higher LET than carbon.

Fig. 9.6

Oxygen-enhancing ration at 10 % survival level measured in vitro for various ions as a function of LET (Image reproduced from Ref. [9])

The oxygen effect seems to show a general trend that high LET radiation, is equally effective for resistant cells, be it due to cell-cycle dependence, oxygenation, or resistant stem cells (see Ref. [23] for details).

9.4 Therapy Planning

Radiotherapy treatment planning for heavier ions is very similar to proton therapy planning from the physical point of view. Typically pencil beam models are used, which describe the three-dimensional dose arising from a single mono-energetic beam in water (see [4, 17, 22]). To describe the depth dose distribution, usually tabulated depth dose curves are used, which either rely completely on measured data or use additional Monte Carlo tools to generate a data base from a few measured data [26]. For the lateral dose distribution, typically a superposition of Gaussians is used, which exhibit widths which are varying with depth. The different terms in such an empirical description refer to the primary beam width, which is evolving due to multiple scattering and at least one additional term, which takes into account large-angle contributions, arising from nuclear fragmentation. The nuclear fragmentation is intrinsically included in the depth dose distribution.

Only gold members can continue reading. Log In or Register to continue