15CHAPTER 2
Radiobiology Principles of Radiosurgery and SBRT
At this point in time, there is no rigorous, comprehensive “radiobiology” that covers the multiple effects of radiation therapy. There are serious theories about the true mechanisms of cell killing and microenvironment changes that lead to tumor control and normal tissue complications in the clinical setting (or even in the laboratory). Nonetheless, clinicians and scientists have put together a useful quantitative framework that describes and predicts treatment effects for the full range of treatments including conventionally fractionated treatments and the extreme hypofractionation of stereotactic ablative radiation therapy (SABR, also called stereotactic body radiation therapy [SBRT]). The basic concepts of this framework are described in this chapter.
GENERAL CONSIDERATIONS
The 5 Rs
Both the benefits and dangers of ionizing radiation for treatment of cancer come from the fact that radiation kills cells. Factors that alter cell killing efficacy were summarized long ago by the “4 Rs” of radiobiology:
1. Repair: Radiation produces both lethal and sublethal damage. Given enough time, sublethal damage to a tumor cell may get repaired so that the cell retains the ability to divide and produce progeny that can divide indefinitely and perhaps metastasize. For a normal organ, repair means that an initially damaged cell regains or keeps its ability to contribute to organ function. See references (1-3) for details about the dominant radiation damage and repair mechanisms. The time course of repair is usually modeled as exponential or biexponential, with half-times ranging from about 15 minutes to 5 hours or more (4, 5).
2. Repopulation: Tumor cells and many types of normal cells (skin, mucosa, white blood cells) repopulate their environment. To effectively treat a tumor, radiation killing must outpace repopulation so that at the end of treatment, no cells capable of unlimited division (clonogens) remain at the irradiated site. Repopulation can occur while dose is being delivered (as in brachytherapy) and during and between sessions of a fractionated external beam regimen, in which case it is often modeled as exponential growth, sometimes commencing after a “kickoff” time of days to weeks (6). Repopulation during treatment is responsible for the loss of efficacy in long-course radiation therapy regimens, whereas repopulation after treatment is the major (perhaps the only) cause of local recurrence of an irradiated tumor. Although posttreatment repopulation is often modeled as exponential growth, there are other models, among them the Gompertz model, which allow for size-dependent growth of new or recurrent tumors (7).
3. Redistribution: As cells pass through the cell cycle, their sensitivity to radiation damage changes. Because cells in vivo are asynchronous, cells in more sensitive phases are preferentially killed initially, so shortly after irradiation there is an excess of cells that were in the resistant phase during irradiation. The effect of redistribution of cells within the cell cycle eventually restores the original distribution and thereby also restores the initial sensitivity. The effect of redistribution on clinical outcomes and its role in the efficacy of different fractionation schedules is difficult to quantify and remains unclear.
4. Reoxygenation (1, 8): Hypoxia is a common feature of the tumor microenvironment and is known to increase radioresistance. Two types of tumor hypoxia are described in the literature, chronic and acute; the latter, in contrast to the former, is the result of temporary opening and closing of blood vessels inside the tumor. Tumor vasculature is structurally and functionally abnormal and inefficient at transporting oxygen. Hypoxic cells are more distant from microvessels than oxic cells and diffusion limits the amount of oxygen available to them. Furthermore, hyperactive oxic cells consume excessive amounts of oxygen, which reduces oxygen availability beyond what diffusion alone would allow. However, as radiation kills the more sensitive oxic cells, their oxygen use decreases and hypoxic cells reoxygenate and become more radiosensitive. Because reoxygenation requires days to occur, the impact of hypoxia on outcomes of short-course treatments, as in SBRT, is unclear.
A fifth “R”—radiosensitivity—is sometimes invoked because some tumor histological types are much more radiosensitive than others (9, 10). For example, lymphomas are radiosensitive, whereas melanoma is radioresistant. Normal tissue cells also have a range of radiosensitivities, which may be reflected in different dose dependence of normal tissue complications in different organs. Intrinsic radiosensitivity of tumors and normal tissues may also vary between patients and within individual tumors, even in a single patient.
The Rs apply to cell killing by all types of ionizing radiation. However, because by far the greatest clinical SBRT experience is with megavoltage photons, further discussions and associated model parameters in this chapter are based on the photon experience.
Mechanisms of Radiation-Induced Cell Killing
The Rs described earlier are qualitative observations without mention of the mechanisms by which radiation kills cells. But quantitative assumptions are needed to rationally manipulate treatment schedules and dose distributions to achieve a beneficial therapeutic ratio, that is, high tumor control probability (TCP) and low or clinically acceptable normal tissue complication probability (NTCP). For conventionally fractionated regimens (1–3 Gy/fraction), the overwhelmingly dominant mechanism of cell killing is damage to the double-stranded DNA structure. Specifically, DNA double-strand breaks (DSBs), or perhaps a subset of DSBs, are considered precursors of radiation-induced lethal lesions (11). In vitro experiments, which have been done for decades on numerous cell types by numerous investigators (1), show that for cells exposed to a single dose of densely ionizing radiation (e.g., alpha particles), the logarithm of the surviving fraction (SF) of cells decreases linearly with dose, D (SF = exp[–αD]). For a single dose of sparsely ionizing radiation (kV or MV x-rays, electrons), the logarithm of SF has a “shoulder”—a shallower than linear decrease at low doses—as shown in Figure 2.1.
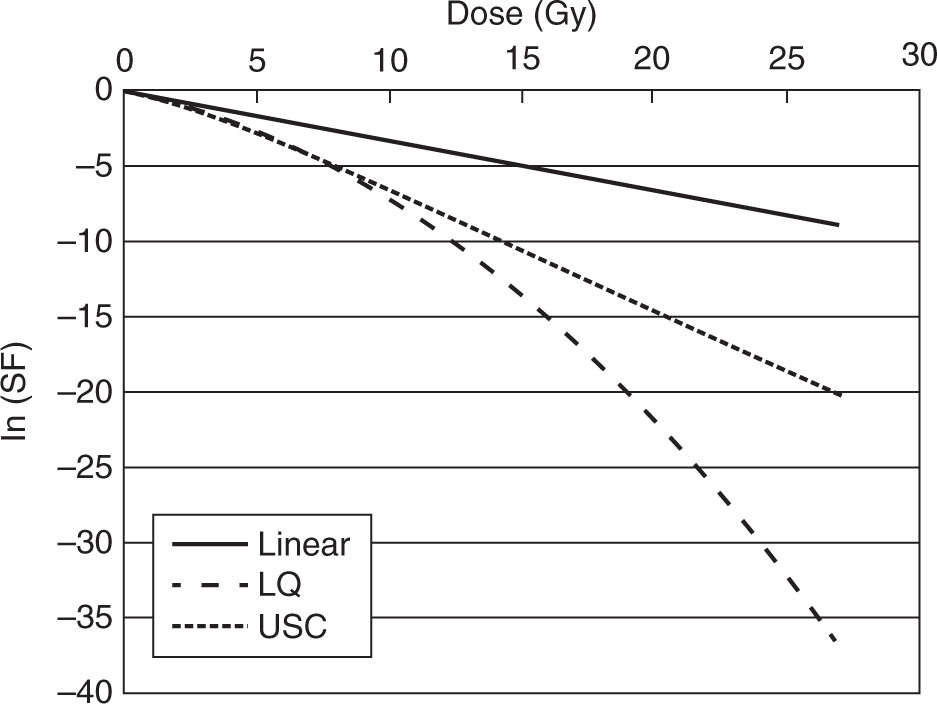
FIGURE 2.1 Single-fraction cell survival curves for three models: the linear model (SF(D) = exp(–αD) with α = 0.33 Gy–1), the LQ model (SF(D) = exp(–αD – βD2) with α = 0.33 Gy–1, β = 0.03835 Gy–2), and the USC model (SF(D) = exp(–αD – βD2) with α = 0.33 Gy–1, β = 0.03835 Gy–2 for D ≤ DT and = exp(–D/D0 + Dq/D0) for D ≥ DT with α = 0.33, D0 = 1.25 Gy, and Dq = 1.8 Gy). These last parameters and α and β for the other two models are from reference (24).
LQ, linear–quadratic; SF, surviving fraction; USC, universal survival curve.
17Linear–Quadratic Model
In vitro single-fraction cell survival curves are well fit by a number of mathematical functions (or “models”) including the linear–quadratic [LQ] model:
![]()
This general behavior persists at least to single-fraction doses up to 10 Gy and is a reasonable approximation up to 15 to 18 Gy (12) but the “curviness” of in vitro survival curves does not continue to ultrahigh doses. Rather, they begin to straighten and approach a purely exponential decrease (13). The radiobiological parameters α and β depend on the cell type and environment but, according to the LQ model, are independent of dose. The linear term is associated with lethally misrepaired DSBs or unrepairable DNA damage formed by a single radiation track, whereas the quadratic term is attributed to two DSBs, formed by two independent radiation tracks traversing the cell, perhaps at two different times (14). Cells have the potential to repair such lesions before the cell’s reproductive capability is destroyed, and this makes a dose delivered in two fractions separated by an interval of time less effective than the same total dose delivered in a single acute fraction. Repair plays an important role in understanding and modeling brachytherapy and in determining a safe interval between external beam treatment fractions. The well-explored Lea-Catcheside formalism deals with repair within the LQ model through a time-dependent factor G, whose effect is to reduce β for protracted irradiations (15, 16[appendix]).
According to the LQ model, the fraction of cells surviving total dose D delivered in n fractions that are spaced far enough apart in time for complete repair of sublethal damage before the next fraction is delivered yet close enough together for repopulation to be insignificant is given by
![]()
which is sometimes written as
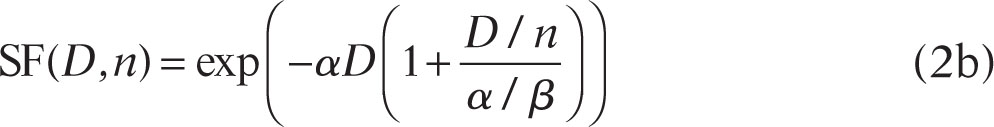
α/β determines the dependence of outcome on dose per fraction and is therefore very important in distinguishing effects of SBRT from conventional fractionation. The 1/n in the quadratic term of Eq. 2a arises naturally in the Lea-Catcheside formalism as the limiting case when the time between successive fractions is much longer than the repair time. For quick calculations, it is common to approximate tumor α/β by 10 Gy. For reasons that are not well understood, α/β is lower—often approximated by 3 to 4 Gy—for late complications (months to years after the end of radiation), whereas for acute complications such as skin reactions, which occur during or shortly after a course of radiation, α/β is approximated by 10 Gy. For hypotheses regarding the systematic α/β differences, see references 5 and 16. Late-responding normal tissue complications are particularly important dose-limiting factors in SBRT. Repopulation during a treatment lasting for time T (including intertreatment intervals and weekends) where growth with half-time T1/2 starts after a “kickoff” time, Tk, is approximated by
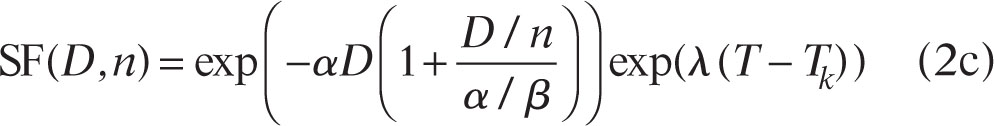
where λ = ln 2/T1/2 and the repopulation term applies only to time T > Tk (6).
The key LQ model parameters are α/β, α, and, for more sophisticated variations, kinetic parameters for sublethal damage repair and repopulation. The fraction of cells surviving a single 2-Gy dose (SF2), which is readily measured in vitro, is sometimes reported instead of α as an efficient metric for comparing cellular radiosensitivity (10, 17). There are many tabulations of in vitro, in vivo, and clinically measured values of LQ parameters, and experimental techniques for determining them are well described in other books (1, 16, 18). For radiosensitive tumors (e.g., lymphomas), α ~ 0.7 Gy–1, whereas for radioresistant tumors α ~ 0.26 Gy–1 (10). Repair half-times range from approximately 0.25 hour to over 5 hours. Tumor repopulation half-times during radiation treatment range from less than a day to several weeks. Measured volume doubling times for untreated new, recurrent, or metastatic tumors are months to several years, generally longer than the “potential doubling time,” Tpot, of pure repopulation because of competing effects of cell loss, cell cycling, and microenvironmental limitations (1, 7, 19, 20).
Hypoxia increases radioresistance. The oxygen enhancement ratio (OER), which depends on the type of radiation and the biological effect of interest, is defined as the ratio of dose for effect under extreme hypoxic conditions to isoeffective dose with the oxygen level under investigation (often normal oxygen levels). As a function of oxygen partial pressure, OER rises steeply as the oxygen partial pressure increase from 1 mmHg for extreme anoxia to approximately 20 mmHg, but thereafter it changes only slightly with increasing oxygen tension. OER is often approximated 18as 3 for photon radiation therapy (1[Chapter 6], 17[Chapters 15–17]). OER values for the end point of cell death are relatively constant over a large dose range (possible slight increase with dose: (1). Within the LQ model, Eq. 1, 2a, 2b, or 2c implies that hypoxia reduces α by a factor of OER and β by a factor of (OER)2. Carlson et al. (21) have statistically tested this hypothesis against a large number of in vitro datasets and shown that this is a reasonable assumption.
Other DNA Damage Models
In vitro studies at high (>10–15 Gy) single-fraction doses provide evidence that cell kill is overpredicted by the continuously bending quadratic term of ln(SF(D)) and that a simple exponential is more appropriate in this dose range. In more complex in vivo settings, there are multiple confounding variables and it is not clear whether breakdown of the LQ model is clinically observed (22). Nonetheless, it is known that LQ is an approximation that can be derived from several models that include mechanisms and kinetics of potentially lethal DNA damage and its repair. These include the repair–misrepair model (23), the lethal–potentially lethal damage model (24), the repair saturation models (25), and the repair–misrepair fixation model (14). There are also many nonmechanistic functions or empirical models that introduce parameters to straighten out the ln(SF) curve at high doses where this effect might impact SBRT outcomes. One such model that is cited in some SBRT outcome-related publications is the “universal survival curve” (USC) (26), which changes from LQ to exponential at a threshold dose (DT) while remaining continuous and with a continuous derivative. Figure 2.1 shows a comparison of ln(SF) curves for the linear, LQ, and USC models with a matching choice of parameters.
In their simplest forms—ignoring kinetic effects—these other models require that more parameters be determined from data than the LQ model, which requires only two (α and α/β). For “back of the envelope” calculations to determine approximately equivalent treatment schedules, the LQ model has many advantages: Only the single experimental parameter α/β is needed, one must at worst solve a quadratic equation, and LQ can be used fairly confidently even up to 15 to 18 Gy. No model to date offers sufficient advantages over the LQ model to replace it as an important clinical tool. Sufficient clinical evidence to support the use of any of the alternative models at high fraction doses in clinical practice is also currently lacking (27).
Mechanisms for cell killing at high fraction doses that do not rely on DNA damage have also been proposed and are discussed briefly in the following text but currently they have no accompanying mathematical models.
Cell Killing by Means Other Than DNA Damage
The high fraction doses given in SBRT have prompted investigation into other cell-killing mechanisms, especially for tumors. Brown et al. (22) have recently critically reviewed the evidence for and against these potential high-dose mechanisms. Among them are the following:
Radiation-induced vascular damage: Tumor microvasculature often differs from normal in that it is tortuous, irregular, and thin-walled. Destruction of these vessels by high doses (above approximately 10 Gy) has been reported in animal models, and mechanisms for this damage have been proposed (28, 29). Although there is insufficient clinical evidence at this time, vascular effects have been proposed as a reason for superior tumor control in SBRT (30). On the contrary, there is evidence against this mechanism, suggesting that tumor cells, rather than endothelial cells of the vasculature, remain the critical targets that regulate tumor eradication by high doses (22).
Immunogenic effects: It has been suggested that the high fraction doses applied to a tumor by SBRT treatments promote both local and systemic immune responses and may potentiate tumoricidal effects of immunotherapy. In the abscopal effect, this may cause tumors distant from the irradiated site to regress and might prevent further development of subclinical metastases. Although there is little clinical evidence, there is evidence from animal experiments and a number of clinical trials are underway (31, 32).
“Bath and shower” effects in normal tissues: Several elegant animal (rat) experiments found that surrounding a high-dose length of cord (the shower) by a longer length low-dose bath strongly reduces the tolerance dose of the high-dose region. A similar effect has been reported in rat parotid glands. But the degree to which these effects are seen clinically in normal tissues or tumors is not known (33, 34).
Neither vascular nor immunogenic effects have been systematized into mathematical models, 19although efforts have been made to model the bath and shower effect (35). Robust clinical evidence is needed to determine the extent to which these novel mechanisms play a role in SBRT treatments.
Biologically Effective Dose
The biologically effective dose (BED) is widely used to compare radiation treatment schedules. The BED concept is not restricted to the LQ model, although that is its most common use. Given a dose-based model for a specified biological effect, two regimens are biologically equivalent if they have the same biological effect (e.g., same TCP, same NTCP for a particular complication). In this case, we have
![]()
where {qi} refers to nondosimetric aspects of treatment. The higher the BED, the greater is the biological effect. If the effect of concern depends mostly on cell kill, BED can be defined as
![]()
where SF is calculated from the model being used.
For example, in the simple (no time dependence) form of the LQ model, the BED for dose D delivered in n fractions is
![]()
Repopulation during treatment lasting for T days, for T > Tk, is commonly added as follows:
![]()
However, for many applications, including the short-course treatments of SBRT, estimations using Eq. 4a are sufficient.
Note that when comparing the effectiveness of different fractionation schemes without repopulation, such as comparing conventional to hypofractionation, α, which is common to both schemes, cancels out, leaving only one biological parameter, α/β. Sometimes it is convenient to compare the effect of a dose given with a novel radiation schedule with the isoeffective dose delivered at the familiar 2 Gy per fraction by using the equivalent dose in 2-Gy fractions (EQD2α/β), often called normalized total dose (NTD). In the LQ model, this is defined as
![]()
As an example, for a tumor with α/β = 10 Gy, the BED of 60 Gy delivered in 30 fractions of 2 Gy each is 72 Gy and EQD210 is 60 Gy. However, the BED and EQD210 of 60 Gy delivered in three fractions of 20 Gy each are 180 and 150 Gy, respectively. Thus, according to the LQ model without repopulation, 60 Gy in 3 equal fractions, a regimen used in early SBRT treatment of non–small-cell lung cancer (NSCLC) (36), is the equivalent of a 75-fraction course of conventionally fractionated radiation (i.e., a total of 150 Gy in 2-Gy fractions). If a late-responding normal tissue (e.g., mainstem bronchus, nearby parts of lung), with α/β =3 Gy, is sufficiently close to the tumor to receive the full prescription dose, then normal tissue BED and EQD23 are 100 and 60 Gy, respectively, for the conventional schedule but are 460 and 276 Gy, respectively, for the hypofractionated schedule. This predicted extreme effect of hypofractionation on late-responding normal tissue is a major reason that safe SBRT requires strict patient immobilization and target localization during treatment as well as very sharp dose gradients that minimize the volume of dosimetrically “close” normal tissue. A dose–volume histogram (DVH) is easily converted to a BED-VH or an EQD2-VH for a chosen α/β by converting dose to BED or EQD2 in each dose bin. Such conversion is often, but not always, done in papers on outcomes of SBRT and is particularly useful when comparing or combining SBRT studies with different fractionation regimens. Figure 2.2 compares the target and the ipsilateral normal lung DVHs and EQD2-VHs for the common lung SBRT prescription of 12 Gy × 4 fractions.
As a second example, there is much evidence that for prostate cancer, α/β is low, ~1.5 to 3 Gy (37–40), much lower than the generic “tumor” value of 10 Gy. Typical SBRT regimens for low- to intermediate-risk prostate cancer are 7 to 8 Gy × 5 fractions, often given every other day to minimize normal tissue toxicity (41). These regimens correspond to EQD21.5 values between 85 and 108.6 Gy (or EQD23 of 70–88 Gy). The highest conventionally fractionated prostate prescription is an 8- to 9-week (48 fractions of 1.8 Gy) treatment course of 86.4 Gy (42) corresponding (without repopulation) to a comparable tumor EQD21.5 of approximately 76.5 Gy (EQD23 of 82.9 Gy). With meticulous image guidance, strict normal tissue constraints, and often special rectal immobilization or displacement methods, reported toxicities of prostate SBRT out to 3 to 5 years have been acceptable and the convenience of the much shorter treatment course is an important practical factor. But, because prostate cancer recurrence and some urinary complications may occur years after treatment, further follow-up is needed for fair comparison with more conventional schedules.
20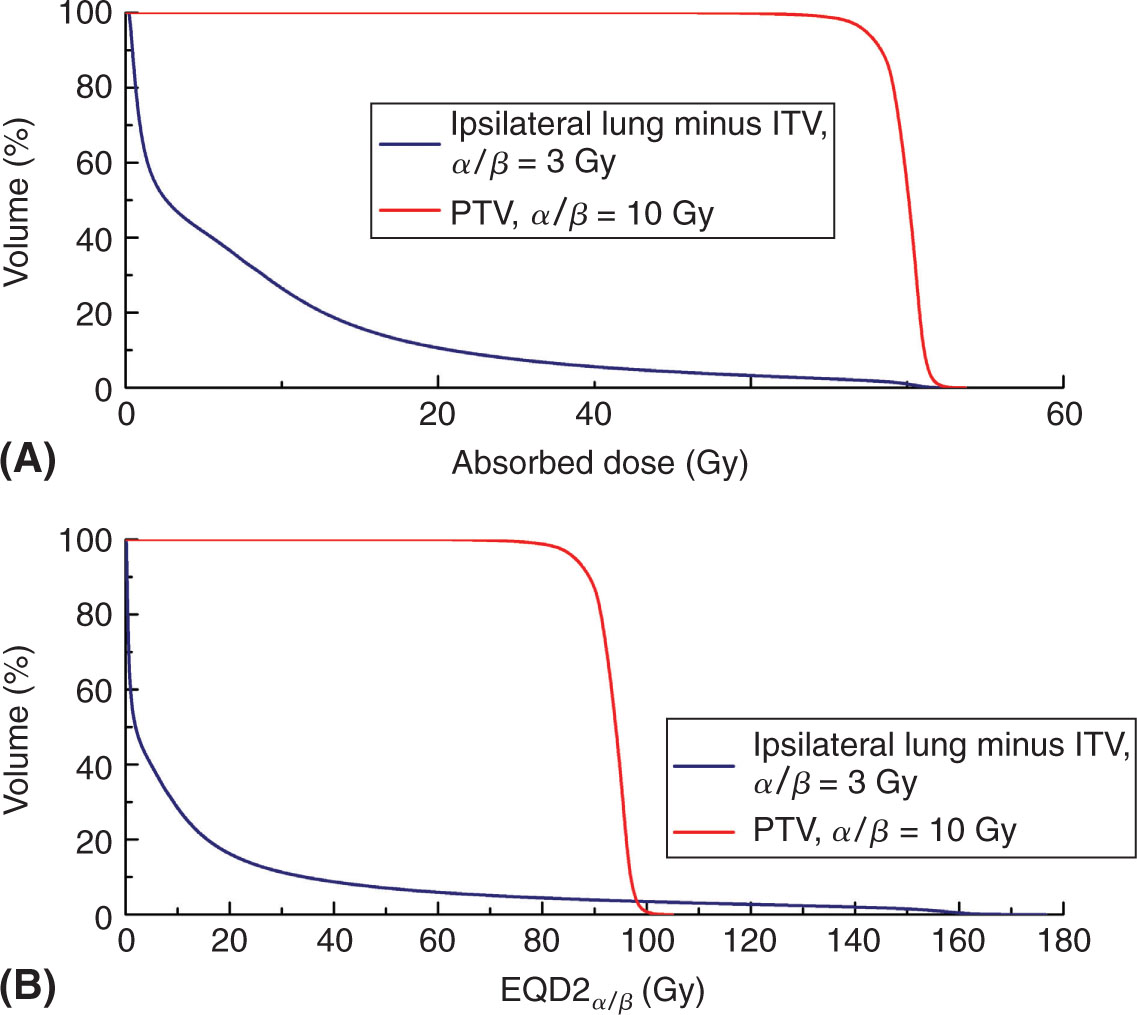
FIGURE 2.2 PTV and ipsilateral lung minus ITV DVHs (A) and EQD2_VHs (B) for tumor (α/β = 10 Gy) and ipsilateral lung minus ITV (α/β =3 Gy) for a typical SBRT regimen of 12 Gy × 4 fractions.
DVH, dose–volume histogram; EQD2, equivalent dose in 2-Gy fractions; ITV, internal target volume; PTV, planning target volume; SBRT, stereotactic body radiation therapy.
TUMOR CONTROL PROBABILITY
TCP is the probability that, after treatment, the treated tumor ceases to grow to a detectable size during the patient’s entire life (43). It is an inherently population-based concept that is observable for a patient cohort but not for an individual. The measurable clinical end point for TCP is local tumor control. Metastases at untreated sites and new primary tumors do not count in evaluating TCP, although the competing risk of death is an important factor in analyzing clinical outcomes.
A commonly used criterion for a radiobiology-based mathematical model of TCP is the fraction of cases in which the treatment has eliminated all the clonogenic cells—that is, all the cells at the irradiated site that are capable of reproducing without limit and eventually regrowing the tumor. It is important to realize that there are also nonclonogenic cells in a tumor—some are normal, some are genetically abnormal, and some are stromal cells such as the necessary vasculature or small lung airways that are surrounded by tumor. The probability p that a clonogen does not survive a therapy regimen represented by {qi} is (1 – SF({qi})). If the tumor consists of N identical clonogens, all receiving the same treatment regimen and radiation-induced cell killing events are independent (which may not be the case in the presence of immunogenic or vascular damage effects) and randomly distributed, and there is negligible repopulation during treatment, the surviving clonogen distribution is approximately poissonian and the probability that no clonogens survive is (44)
![]()
Under these conditions, for n equal treatment fractions that give uniform dose D to the tumor and are spaced far enough apart for almost complete repair, TCP assuming the simple LQ model (no time dependences) is
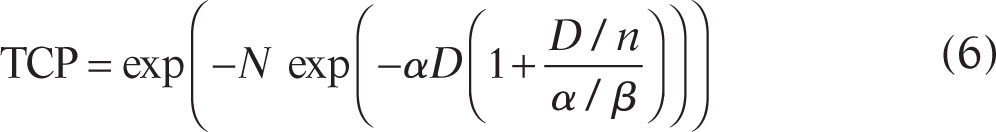
Repopulation during treatment is usually handled by including an exponential growth term as in Eq. 4b. This invalidates the Poisson distribution assumption and a more accurate formalism was published by Zaider and Minerbo (45), although few investigators apply the more complex equations derived in that reference to clinical outcomes.
An extension of the Poisson TCP formalism to inhomogeneous tumor dose distributions and to 21tumors with spatially varying clonogen radiosensitivity, such as might arise from hypoxia, was developed by Brahme and Agren (46) and by Goitein (47) and Niemierko and Goitein (48). Modern functional imaging technology allows us to quantitatively infer tumor characteristics, such as cell concentration or hypoxia, from PET and MRI, making such formalisms particularly useful (49). The tumor is divided into voxels (Goitein called them “tumorlets”), usually of equal volume, vi, which is small enough so that it has uniform dose Di and/or radiosensitivity (αi, βi). If the clonogen density of the ith voxel is ρi, it contains ρivi clonogens and the TCP in that voxel (TCPi) is given by
![]()
Local control is achieved if no voxel contains surviving clonogens, or
![]()
and
![]()
Given a treatment plan, the voxel-by-voxel dose to use in SFi is obtained from the differential DVH of the tumor. Different SBRT studies use very different target dose distributions. If the target surrounds a critical normal tissue, it might be preferable to have an approximately uniform target dose, or to have a central cold spot if tolerance of a central normal tissue is more important than target coverage. But often, following the precedent of cranial stereotactic radiosurgery, the target dose is highly nonuniform (e.g., Radiation Therapy Oncology Group [RTOG] trials 0236 and 0618) with the dose at the approximate center of the planning target volume (PTV) being 20% to 50% higher than at the periphery. Figure 2.3 shows idealized typical SBRT DVHs. Publications that describe outcomes usually cite prescription doses and sometimes the prescription isodose, but few publications provide detailed dose distributions. The fallback position for analyses of published data, especially those combining data from several studies, is to assume either, conservatively, that the clonogens receive uniform prescription dose or that they receive an estimated, higher central dose.
Simpler TCP Dose–Response Formulas
Simpler functions with no cellular radiobiological foundations are useful in demonstrating important relationships between TCP and dose distributions. TCP is expected to increase monotonically from almost 0 at very low doses to 1 at sufficiently high doses (Figure 2.4). A minimum of two parameters define the dose–response curve: D50 (or BED50 or EQD2α/β50 depending on the “dose”-axis variable), which sets the dose at which there is tumor control in 50% of a population, and γT%, the percent change 22in TCP per percent change of dose at the point where TCP equals T% (50). Most commonly, γ is specified at TCP = 50% and called γ50. If γ50 is small, TCP increases gradually with dose. D50 and γ50 can be measured, both clinically and in animal models.
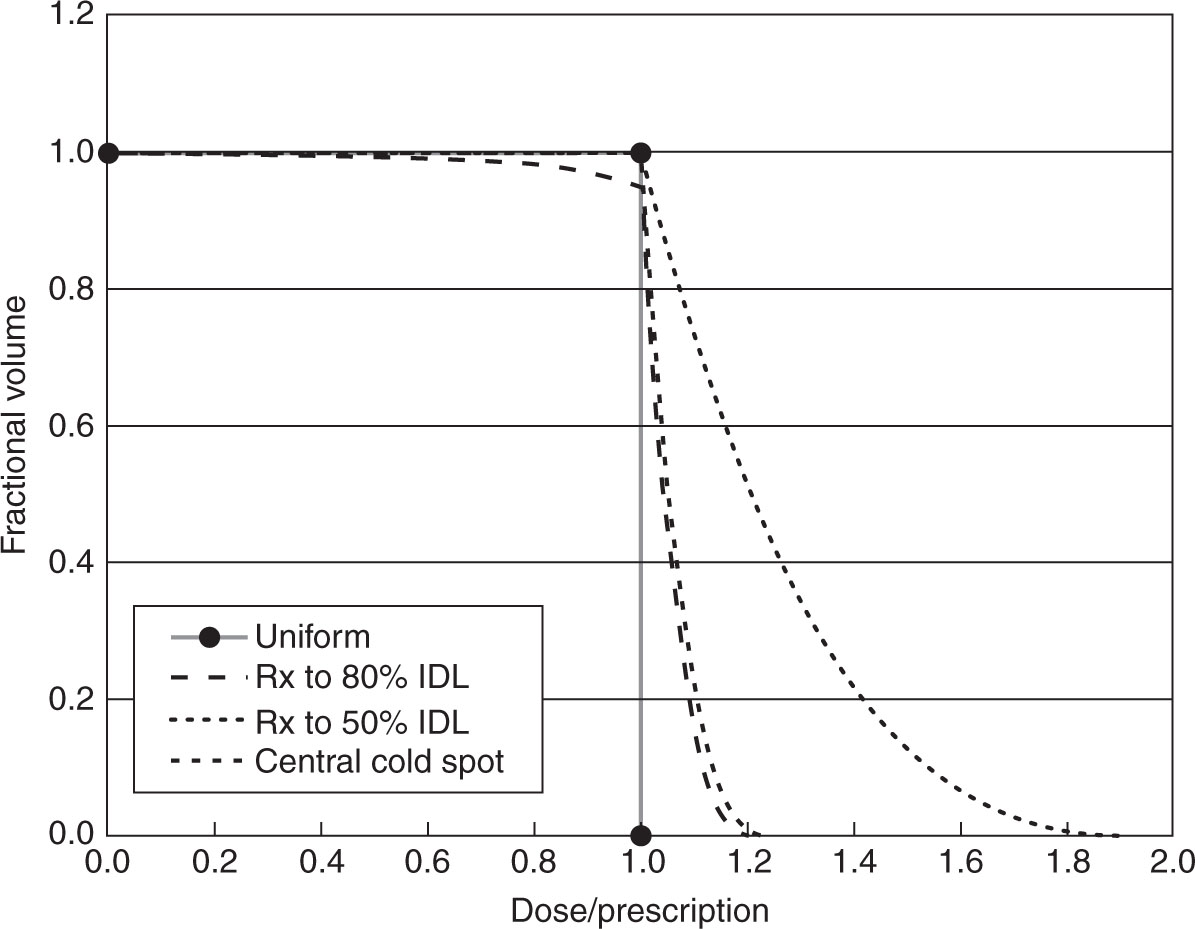
FIGURE 2.3 Idealized integral target DVHs for typical SBRT cases. Triangles are the ideal (but unattainable) uniform dose distribution. However, for SBRT, it is common to not want a uniform target dose, but rather to prescribe to a low isodose (with 100% at the target center); the large and small dotted lines are DVHs for prescription dose to the 80% and 50% isodose surface. Finally, SBRT treatments must protect a critical structure within the PTV (e.g., paraspinal cases where the PTV surrounds the spinal cord) that requires a central cold spot.
DVH, dose–volume histogram; IDL, isodose line; PTV, planning target volume; SBRT, stereotactic body radiation therapy.
The log-logistic function is a commonly used expression. If the SF of clonogens for a tumor that receives a uniform dose D is given by a log-logistic function 1/(1 + (D/D50)k), then TCP for a uniform dose D is (1 – p) or
![]()
where k = 4γ50. For a nonuniform dose distribution, {Di, vi}, we have
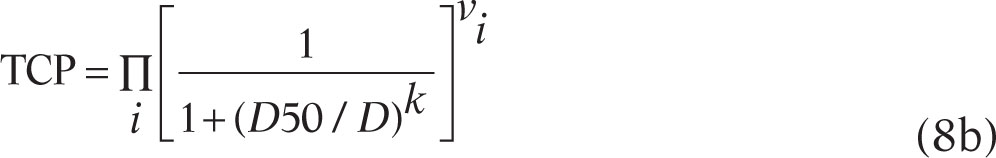
where vi is the fractional volume of the voxels (or tumorlets) receiving dose Di. Tumorlets with different radiobiology are handled with tumorlet-specific D50s and ks.
A logistic function is another frequently used expression:
![]()
Biologically effective doses (BEDs) can be used instead of D and D50.
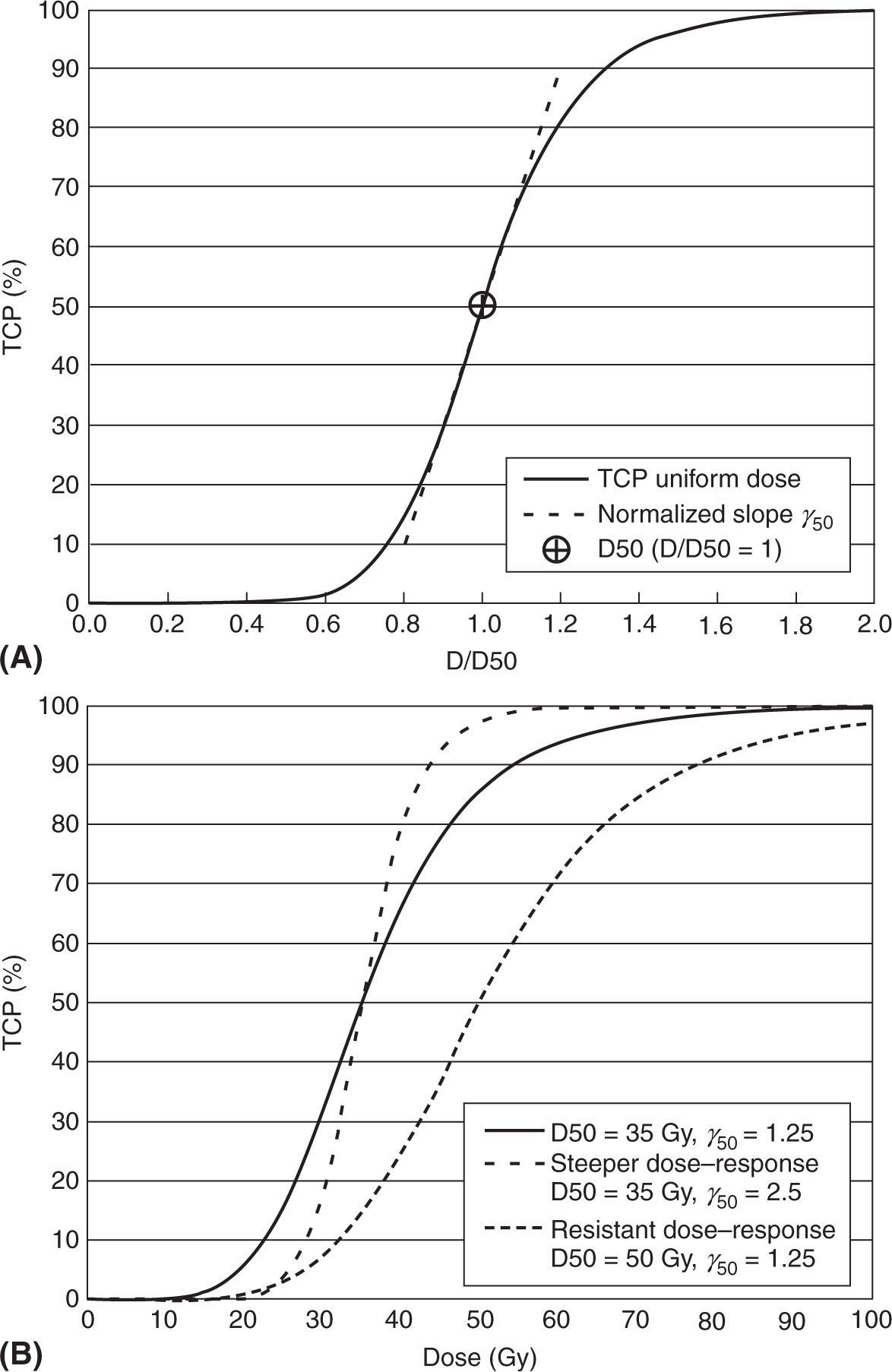
FIGURE 2.4 (A) A typical sigmoidal curve (log-logistic equation) with the definitions of D50 and γ50. (B) Comparison of the effects of changes in D50 and γ50.
TCP, tumor control probability.
23Finally, sometimes the Poisson expression (Eq. 5–7) may be used. Although it might be regarded as more basic, it also requires more input parameters about which there is greater uncertainty. There are no universal standards.
As a simple example, consider a tumor with a log-logistic dose–response with k = 8 (γ50 = 2) and uniform radiosensitivity. As shown in Figure 2.5, a deep but volumetrically small cold spot (30% of the dose to 10% of the volume) causes notable decrease in TCP compared with uniform dose—indeed, even a very small subvolume with zero dose results in zero TCP because the clonogens in that protected subvolume survive. But a 30% hotspot to 10% of the volume has little effect because TCP is dominated by survival of the clonogens in the majority of the volume. Because the x-axis is D/D50, the identical arguments apply to a situation in which the dose is uniform but the clonogen radiosensitivity is variable. Specifically, the dashed TCP curve also applies when the tumor receives uniform dose but the cells in a 10% subvolume are 43% more radioresistant cells (D50′ = 1.43D50). If this subvolume can be identified (e.g., with some form of molecular imaging), boosting its dose by 43% would restore the TCP of the solid curve. Thus, directing a hot spot to a known high-risk subvolume is beneficial, even though a randomly placed hotspot is not. Similarly, the “30% higher dose” curve for a biologically uniform tumor also applies to a uniform dose applied to a tumor in which 10% of the clonogens are more radiosensitive (D50′ = 0.77D50). Even though the tumor has a small radiosensitive component, the radioresistant cells dominate the response. For examples of similar exercises, see references 51 (with the log-logistic function) and 52 (with the Niemierko/Goitein formalism of reference 48).
A TCP Puzzle
Although the mechanistically motivated Poisson dose–response is given by Eq. 6, an interesting question arises when the model is used together with the straightforward assumption of identical radiobiological parameters for all clonogens. To more cleanly see this, assume that β = 0 and the dose is uniform. Then, we get
![]()
![]()
D50 depends on both the radiosensitivity (α) and the number of identical clonogens (N), whereas γ50 depends only on the number of clonogens. The cell density in soft tissue is 108 to 109 cells/mL so the number of cells in a tumor of volume V is ~109V. But the fraction that is clonogenic is unknown, as is the clonogen distribution within the target volume.
Although N is unknown, reasonable order-of-magnitude assumptions lead to predictions that disagree with observation. As N varies from 100 to 108, the calculated γ50 varies from 1.7 to 6.5. Thus, if all the cells in a 1-mL tumor were clonogenic, γ50 would be at least 6.5 and the dose–response for larger tumors would be even steeper. However, values 24of γ50 in clinical studies are typically 1 to 3 (9, 50), regardless of tumor size. Taking Eq. 9a and 9b literally implies that tumors have fewer than 1,000 clonogenic cells, regardless of size. Even in animal studies, where conditions can be tightly controlled, γ50 is below 4 (53). In addition, if the number of clonogens scales with the tumor volume, the simple LQ model predicts a much stronger dependence of TCP on volume than is observed (47). These problems persist for other DNA-damage models, as they are rooted in the Poisson statistics definition of TCP.
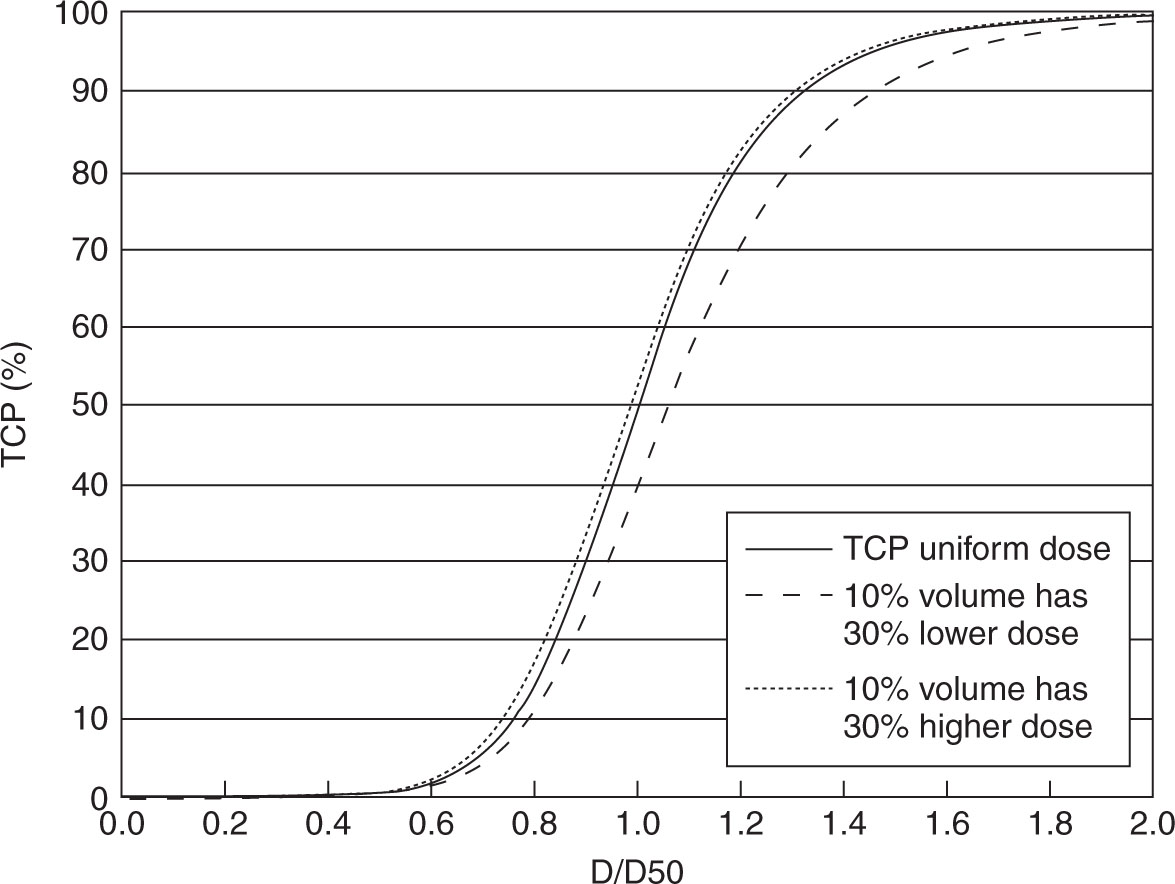
FIGURE 2.5 Effects of nonuniform dose/uniform clonogen radiosensitivity on TCP. As described in the text, this also describes the effect of uniform dose in a tumor with nonuniform radiosensitivity.
TCP, tumor control probability.
One Solution: Fit Dose or BED to Local Control Observations
Many published studies do not worry about this seeming paradox and, by clever use of available data, rather than starting a model from scratch, answer important questions. For example, Fowler et al. (54) started from a NSCLC TCP dose–response obtained from a single institution’s conventionally fractionated dose escalation study with prescription doses ranging from 60 Gy to approximately 100 Gy. At 2 Gy per fraction, they estimated treatment times from 39 to 67 days, including weekends. Using repopulation kinetics on the basis of clinical observations of loss of local control in patients who experienced treatment delays in an earlier RTOG trial, they argued that the main tumoricidal advantage of SBRT comes from its elimination of repopulation during the much shorter treatment schedule (Figure 2.6).
As a second example, in general, the data for the more common SBRT treatments, though quite noisy, clearly suggest a dose–response and for NSCLC, brain metastases, prostate, and spinal tumors, clinicians now prescribe schedules that have been reported to be successful and safe. An analysis of a large set of patients (811 lesions in 657 patients) treated with single-fraction SBRT for paraspinal tumors over 12 years at a single institution found that the gross target volume (GTV) and PTV D95 were highly significant predictors of local control. Although these were all metastatic patients, the mean overall survival was 26.9 months. The best cut point distinguishing “low” from “high” dose was 18.3 Gy for GTV D95 and 17.4 for PTV D95. The cumulative incidence of local failure at 48 months was 2.1% for the high-dose cohort, 14% for the low-dose GTV group, and 20% for the low-dose PTV group, independent of the primary tumor’s histological type. Because all cases were treated with a single fraction, no “BED” conversion was necessary to compare outcomes (55).
Meta-analyses of publications that include local tumor control data for a variety of fractionations often do not need to consider full model-predicted TCP, but rather investigate the fit of outcomes data (y-axis) with the BED or EQD determined by a chosen model (x-axis)—as an example, see Figure 2.7. Several analyses (including references 27, 56–58) of large, single-institution or pooled published data that include different SBRT fractionation schedules for NSCLC find that local control and overall survival are significantly better for treatments with LQ BED10 (BED with α/β = 10 Gy) above 100 to 105 Gy: These include the popular schedules of 3 fractions × 18 or 20 Gy and 4 fractions × 12 Gy. For stereotactic radiotherapy (SRT) of brain metastases, a systematic review (59) identified only 11 of 260 papers published between 1990 and 2009 that met their search criteria (>10 patients, actuarial local control reported, a single dose-fractionation schedule for all or a well-defined cohort of the study, SRT as primary treatment or treatment for recurrence after whole-brain treatment). Treatments of approximately 1,600 metastases were in this analysis. The authors found that 1-year local control was “excellent after single fraction SRT doses above 20 Gy, but disappointing after doses of 15 Gy or less.” For comparison with fractionated treatments they defined BED with a linear–quadratic–cubic model that accounted for return to exponential dependence of SF at high fraction doses and used α/β = 12 Gy and recommended fractionated regimens above 11.6 Gy × 2 or 8.5 Gy × 3.
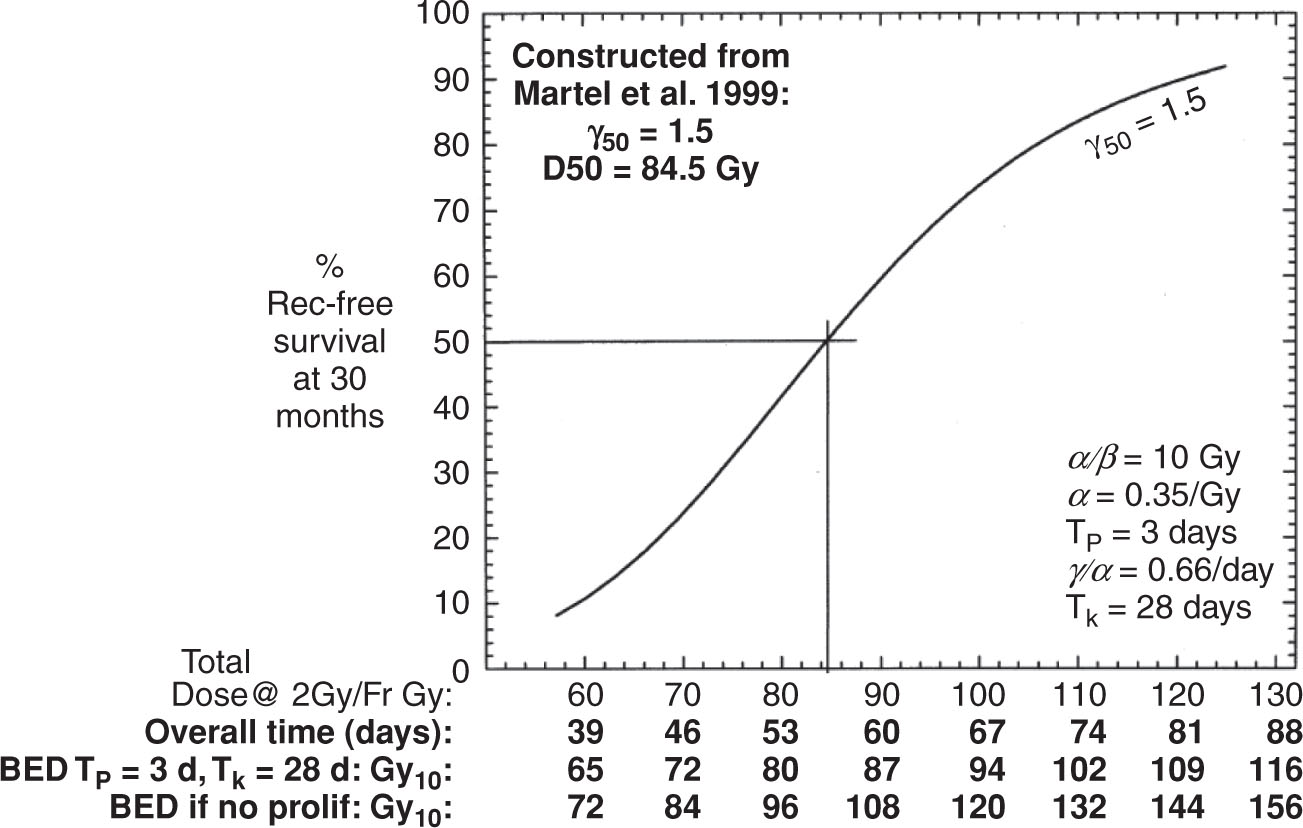
FIGURE 2.6 Short treatment schedules, as with SBRT, increase tumor control (recurrence-free survival) because radiation treatment is not fighting against repopulation during treatment.
BED, biologically effective dose; SBRT, stereotactic body radiation therapy.
Source: Reprinted with permission from Fowler JF, Tomé WA, Fenwick JD, et al. A challenge to traditional radiation oncology. Int J Radiat Oncol Biol Phys. 2004;60(4):1241–1256. doi: 10.1016/j.ijrobp.2004.07.691
25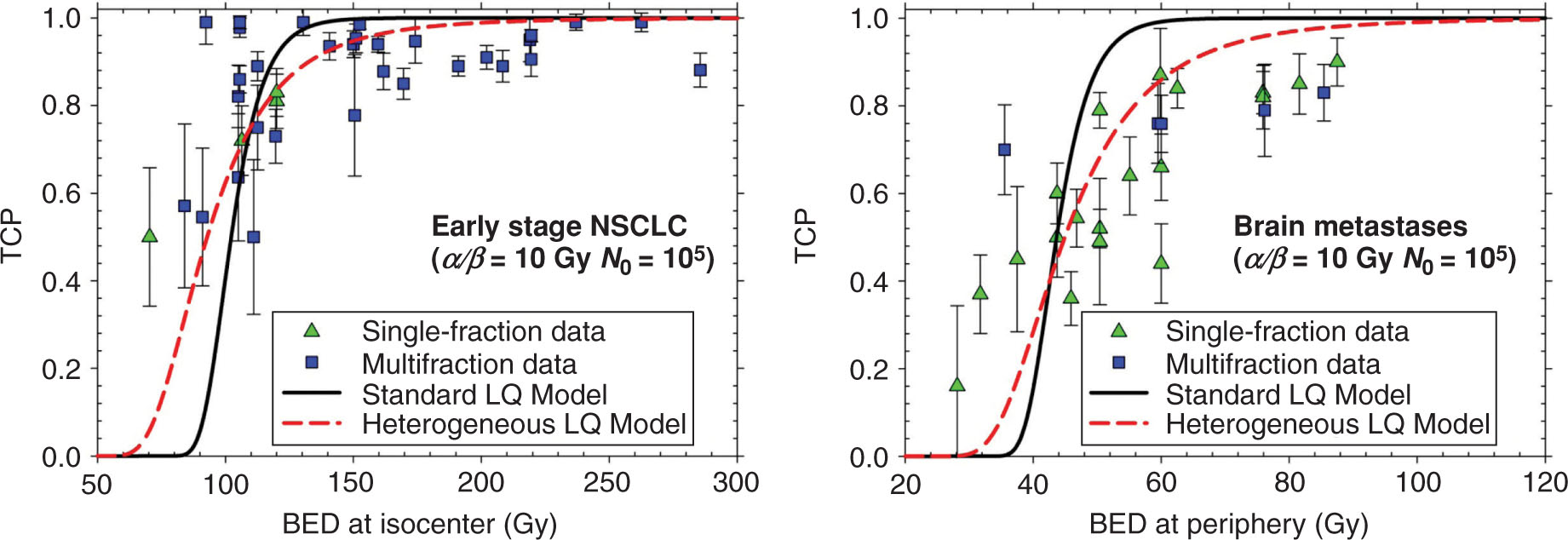
FIGURE 2.7 Data compiled by Shuryak et al. (27) from literature over past 15 years reporting TCP at ≥1 year as a function of BED calculated according to two different models. A dose–response curve—higher BED corresponds to better TCP—is evident.
BED, biologically effective dose; LQ, linear–quadratic; NSCLC, non–small-cell lung cancer; TCP, tumor control probability.
A Second Solution: Population Averaging
To reconcile DNA damage models with realistic clonogen densities, a widely accepted solution to the steep slopes exhibited by Poisson models with what are believed to be reasonable clonogen densities is provided by the observation that even for a well-controlled animal study or patient cohort, there are both interpatient and intratumor variations in radiosensitivity and clonogen number (48, 60–62), such that observed TCP is the weighted sum of multiple dose–response curves, which decreases the γ50 of the observed combination. Figure 2.8 is a simple illustration of the effect of population averaging. Several studies using TCP outcomes of conventionally fractionated treatments take a population-averaging approach, assuming a reasonable clonogen density (e.g., 107 clonogens/mL) and a Gaussian distribution of α (60–62).
Two recent papers used population-averaged models to analyze reported SBRT local control outcomes. It is now well documented that excellent local control is achieved for early stage NSCLC at a LQ BED (α/β = 10 Gy) greater than 100 Gy (Figure 2.8). Shuryak et al. (27) analyzed early stage NSCLC studies (19 studies, 2,028 patients) and brain metastases studies (14 studies, 937 patients) that reported TCP for 1 or more years after treatment. The “heterogeneous LQ model” in Figure 2.7 shows the fit to the NSCLC data from that analysis. The authors assumed that α was distributed over the patient population with a gamma distribution and compared the goodness of fit with published TCP data to the LQ and three other models (linear–quadratic–linear, USC, Pade LQ). The clonogen number was fixed as 105 independent of tumor size and the results were insensitive to α/β varying between 10 and 20 Gy. The LQ model with heterogeneity in radiosensitivity produced the best fit for both NSCLC and brain metastases.
Liu et al. (63) analyzed 1-, 2-, 3-, and 5-year actuarial survival taken from 46 studies of SBRT for NSCLC with six different models, seeking the BED model that gave the best fit to the data with optimized model parameters. Reported doses were converted to isocenter doses when possible. By taking BED as the independent dose variable in the fit, the authors were able to avoid estimating N for all but the newly proposed regrowth model. Five of the models, including the LQ model (one fitting parameter) and the USC (three parameters), did not include population averaging, nor did they account for repopulation by surviving cells after treatment. Data for the different survival time points were analyzed separately for these models. Nonetheless, the best fit to the data, both overall and at discrete time points, was provided by the newly proposed “regrowth model” (six parameters) that assumes exponential growth of the clonogens that remain after treatment, with tumor control reached if fewer than a critical number of clonogens remain. This model includes a population average over the initial number of clonogens. Although the initial clonogen number does not enter directly as a parameter, but rather in the ratio of the critical number of clonogens and in a ratio with the standard deviation of the population distribution, it was taken to be between 104 and 106, independent of tumor size. In this study, α/β was high (~20 Gy) for the best fit versions of all models.
26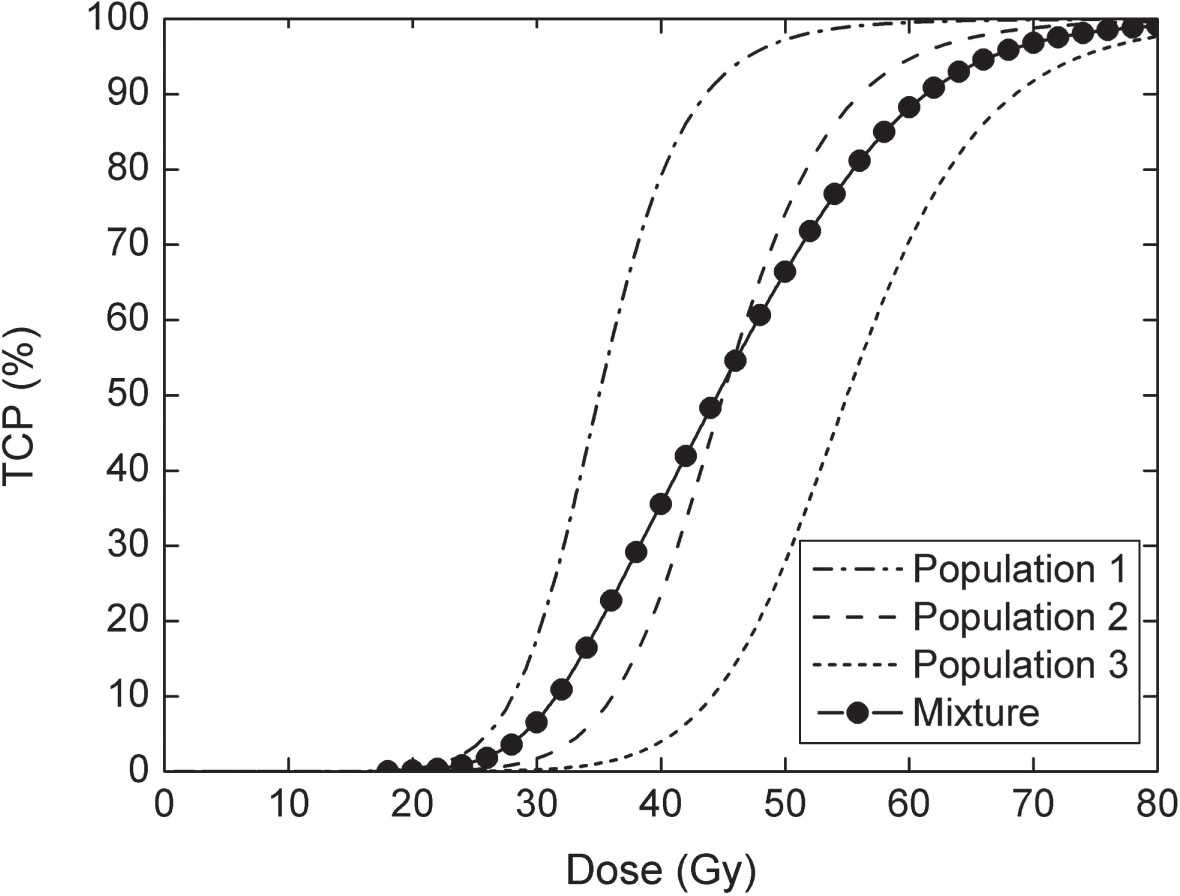
FIGURE 2.8 Example of reduction of Y50 by population averaging. Populations 1, 2, and 3, represented by log-logistic curves, have different D50s (35, 45, and 55 Gy) and Y50 = 2.5 (k = 10). The slope that would be observed from a simple average of the populations (equally weighted populations) is clearly reduced.
TCP, tumor control probability.
Perhaps We Are Asking Too Much
An interesting “uncertainty principle” situation may limit ability to extract fundamental radiobiological parameters from observed TCP data, regardless of their quality. In a theoretical study, Carlone et al. (64) started from a general LQ plus exponential growth model, assuming an independent Gaussian population distribution of each model parameter (N, α, β, and λ) and found that “limited radiobiological information can be determined by the analysis of dose response data: information about parameter ratios can be ascertained, but knowledge of absolute values for the fundamental radiobiological parameters will require independent auxiliary measurements.”
Equivalent Uniform Dose (EUD)
The EUD was introduced by Niemierko (65) as a way to quantitatively rank TCP efficacy of rival treatment plans (with nonuniform dose distributions) without worrying about such microscopic details as the number of clonogens. In this context, EUD is defined as the uniform dose that gives the same TCP as the actual dose distribution given in the same number of fractions. This initial formulation of EUD is based on the LQ model and a key parameter is the SF at 2 Gy, SF2. Niemierko showed that, if the volume fraction getting dose Di is vi and a chosen reference dose is Dref, the EUD for the inhomogeneous dose distribution is
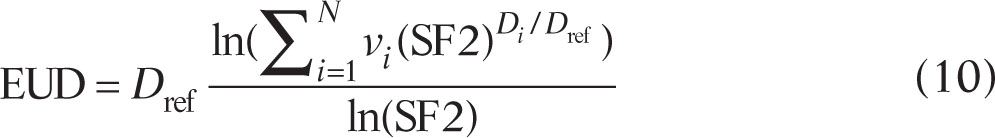
where the sum is over all the subvolumes of the tumor. Expressions were also derived for the full LQ model, for tumors with nonuniform distributions of clonogens, and for a population-averaging model. A minor problem with this definition of EUD is that if the dose to a subvolume is zero, EUD is not zero, which is contradictory to the intuitive idea that a tumor is not controlled if a subvolume receives very low or no dose.
However, in a subsequent publication, Niemierko introduced a nonmechanistic but computationally more convenient quantity, the generalized equivalent 27uniform dose (gEUD), which has become far more widely used (66) for plan comparison and even optimization. gEUD provides a unified formalism that can be applied to normal tissues and tumors and it is discussed later in this chapter.
TCP Summary
Although a purely theoretical understanding of TCP for any dose/fractionation regimen remains a still unreachable “promised land” of radiation biology, existing clinical experience and approximate models on the basis of cell killing because of DNA damage can get us a long way toward effective SBRT treatments. Quantitative formalisms have not yet been devised for mechanisms other than those on the basis of DNA damage (30–35) and these need further investigation under protocol conditions to determine their validity and the value of implementing a mathematical framework.
NORMAL TISSUE COMPLICATION PROBABILITY
All radiation therapy carries some risk of accompanying complications in organs that receive dose during treatment. A given organ can experience more than one complication; many of these are described by the QUANTEC group in a special issue of the International Journal of Radiation Oncology Biology Physics (67). As examples, lung complications include radiation pneumonitis, typically during or within the first 6 months following therapy, and radiation fibrosis, typically a late complication, occurring a year or more after radiation. Rectal complications include rectal bleeding, ulceration, fistula, and fecal incontinence (68).
Normal tissue complications are graded according to severity. Several grading systems are in use, including those designed by RTOG and Southwest Oncology Group (SWOG) and, in increasing use, the Common Terminology Criteria for Adverse Events (CTCAE) (69). CTCAE, now up to Version 4.0, is not specific to radiation and does not differentiate between early and late effects. The systems agree on generalities, though not specifics. A crude general description of the rankings is given in Table 2.1.
Publications about normal tissue complications often specify the grades of complication under discussion as “greater than or equal to” a chosen value, such as Grade 2+ or 3+ (G2+ or G3+).
Although no complication is desirable, the risks and implications of a specific complication must be balanced against the risk of tumor recurrence or ineffective palliation. Achieving this balance is part of the art of treatment planning. Ultimately, the lowest grade of a complication that is clinically “acceptable” for a particular patient is a clinical decision. For example, all modern radiation treatments maintain very low risk of any spinal cord complications (70, 71), often at the cost of undertreating the tumor. For SBRT treatments, which use all the modern tools of image guidance and sharp dose gradients, the risk of Grade 2+ myelopathy is below 1%. On the contrary, a 10% to 20% risk of Grade 2+ lung toxicity or up to a 25% to 30% risk of symptomatic xerostomia is considered acceptable (though certainly not desirable).
TABLE 2.1 General Description of Normal Tissue Complication Rankings
Grade | Symptoms |
0 | None |
1 | Subclinical (radiological or other tests) |
2 | Mild; worthy of mention to a physician but manageable with over-the-counter medications or other conservative means; minimal interference with ADL |
3 | More severe, clearly interfere with ADL, requiring medical intervention |
4 | Hospitalization may be needed; major interference with ADL |
5 | Death |
ADL, activities of daily life.
Unlike tumors, functionality of most normal organs at risk (OARs) depends on the integrity of several different cell types including the endothelial cells that make up the organ’s vasculature, epithelial cells (gastrointestinal tract, lung), muscle cells, hepatocytes (liver), neurons and glial cells (central nervous system [CNS] organs), and other specialized cells peculiar to the organ. Some complications are the result of radiation-induced microenvironmental effects (e.g., radiation pneumonitis, where damaged cells secrete proinflammatory substances) (72). Nonetheless, the LQ model can often be used for quantitative analysis of normal tissue complication risks at different fractionation schedules (1, 5, 15) where it is assumed that the probability of the abnormal organ function of interest is an increasing function of BED or EQD2, calculated with Eq. 4a or 4c. α/β may be different for different complications in the same organ, although whether that is because of different target cells or noisy and limited data is not 28clear. For conventional fractionation, α/β is high (~10 Gy) for acute complications and low (≤5 Gy, often taken as 3 Gy) for late (more than half a year after radiation) complications. Values similar to those obtained from clinical outcomes at conventional fractionations have given reasonable results in outcome analyses of SBRT. Tables of α/β ranges associated with specific complications are Table 8.1 in reference (5) and Tables 3.1 and 3.2 in reference (15).
A wide range of half-times, on the order of 0.5 to 1.5 hours, are reported for repair of normal tissue sublethal damage and there is evidence of biexponential kinetics for some tissues with a second 3- to 6-hour component (15, 17, 73, 74). The common clinical rule of “at least 6 hours between treatments” for twice-daily treatments is based on clinical observations that imply loss of repair for more closely spaced treatments. There is also evidence of reduced rectal (75), carotid artery (76), and lung (77) toxicity when SBRT treatments are delivered on alternating days, as opposed to daily.
Dose–Volume Effects
For most complications, there is a “volume dependence,” that is, NTCP depends on the dose distribution within the organ as well as on dose and dose per fraction. Volume dependences are sometimes described as “serial” or “parallel,” stemming from a conceptual model of how components are organized to carry out an organ’s function (78). The literature often describes the response of multicellular “functional subunits” (FSUs) such as nephrons or alveoli rather than single cells. For a serial organ or complication, the FSUs are arranged in series (sometimes compared with bulbs on a string of Christmas tree lights) and if one is incapacitated, organ function is destroyed. Damage is more likely at higher BED, so serial complications depend on the highest doses in the organ and constraints are often placed on Dmax or Dvery small volume, whereas lower dose regions are of less interest. Observationally, spinal cord, brainstem, and optic structure complications are largely “serial type” and in treatment plans their DVHs are evaluated accordingly. In parallel organs (or for parallel-type complications), the contributions of the FSUs to organ function are redundant and a critical volume (or critical fraction) must be incapacitated to impair organ function (79–80). Parallel-type complications depend strongly on the irradiated volume; often, NTCP is correlated with the mean organ dose or with the Vdose, the percentage or absolute volume receiving more than a selected dose. For example, V20 is a common plan evaluation metric for lung toxicity, regardless of fractionation. The most common lung, parotid, and liver complications are largely “parallel.”
Some complications do not clearly fall into either category. At conventional fractionation, rectal and esophageal complications have been shown to correlate with the highest dose regions and with medium-dose regions (81, 82); and the “bath and shower” effect mentioned earlier describes a situation in which large low-dose volumes promote a serial-type breakdown of function in the high-dose part of the organ. Complexity is increased in situations in which different parts of an organ are responsible for different complications (68) or damage to two organs increases the probability of a single complication (83). For SBRT treatments, sharp dose gradients, strict immobilization, image guidance, and motion control during treatment are crucial, especially near serial or mixed volume dependence OARs.
Dose–volume (DV) correlates of many normal tissue complications for conventionally fractionated radiation therapy were compiled in the literature reviews of Emami et al. (84) in the early days of three-dimensional conformal radiation therapy (3D-CRT). Most of the information in this review came from outcomes observed in the “2D era.” In 2010, the QUANTEC group (61) published reviews and guidelines for normal tissue DV metrics on the basis of outcomes that also included the 3D-CRT experience and early reports on effects of intensity-modulated radiation therapy (IMRT). Because QUANTEC reviewed publications only up to 2008 to 2009, SBRT-related complications were not addressed for most organs. But currently SBRT is used with increasing frequency at almost every anatomical site, and knowledge about complications is being accrued through local clinical experience, protocols, and information sharing through peer-reviewed publications. Despite difficulties described in “The Lessons of QUANTEC” (Jackson et al. in reference 67) over the past two decades, clinicians have evolved sufficiently safe planning constraints to usually prevent the normal tissue complications of SBRT treatments from exceeding those for conventionally fractionated treatment. But despite meticulous planning and image-guided treatment of generally small targets, complications that are rare or unreported for conventional treatments are sometimes seen in SBRT treatments. Further understanding is needed to deal with unexpected—especially late—complications and to prevent tumor undertreatment caused by overly conservative limits.
29Asbell et al. (85) developed an interesting graphic tool, the DVH Risk Map, for displaying and updating the state of knowledge relating to published SBRT normal tissue constraints (of course, Risk Maps need not be restricted to SBRT treatments). In its simplest form, the user plots as many of the published planning limits for a particular complication as can be found by a literature search. It is useful to group these according to the number of fractions for SBRT. When different studies use different DV metrics, there can be a separate Risk Map for each; for example, for radiation myelitis, some studies use the maximum spinal cord dose and some use the dose to a specified small volume such as 0.1 or 1 mL. Published adverse effects distinguished by a particular symbol and isocomplication curve from a mathematical model can also be plotted in these graphs. From a Risk Map, one can see where one’s departmental constraints lie or, given a new mathematical model, test its predictions against published constraints. The example in Figure 2.9 is a Risk Map for radiation myelitis in SBRT treatment, reproduced from reference (86). The blue diamonds are published constraints that, for radiation myelitis (a serial-type complication), constrain the high-dose end of the dose distribution. Although these limits are not derived from fundamental radiobiology, they are based on empirical observations and local or published patient outcome experiences. As expected from the LQ model, the dose limits are higher for more fractions. The extreme caution with regard to spinal cord complications is evidenced by the fact that there are only nine such literature-reported complications. Those plotted as red crosses are all the Grade 4 spinal complications in a cohort of 318 patients treated at three academic centers in the study by Sahgal et al. (87). The low (green) and high (red) risk limits in the figure are the 1% and 3% levels, respectively, predicted by a model being tested by the authors. Although a 50% spinal cord volume (with no data points) is included as a matter of academic interest, there is no evidence that this has bearing on spinal cord complications, especially for SBRT treatments that involve a much smaller percentage of the cord than many conventional treatments.
NTCP Models
As with TCP, mathematical models help physicians and physicists evaluate competing or novel treatment plans. It is important to recognize that NTCP models are even less mechanistic than those for local control. Rather, they are equations with parameters that have been fit, often by complex statistical methods, to what are frequently sparse data (clinicians do not seek to have complications). The parameters that QUANTEC extracted from literature reviews of mostly conventionally fractionated treatments, for which the dose per fraction, fraction number, dose gradients, and relationships between planned and delivered doses are all different, should not be assumed to apply to SBRT regimens without cautious validation. But these parameters, sometimes modified to give the same EQD2, and associated models provide a necessary starting point for single and interinstitutional clinical studies.
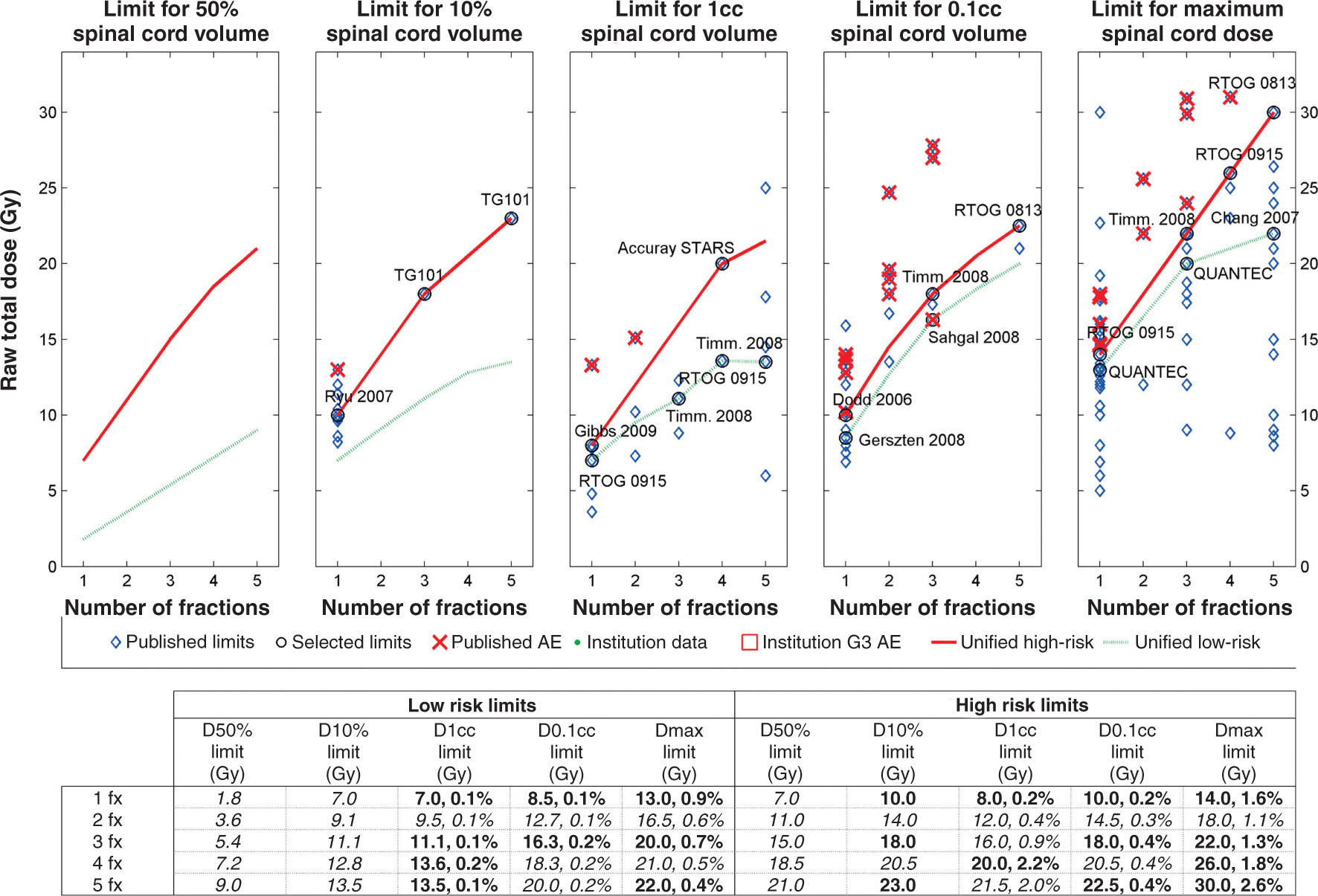
FIGURE 2.9 Risk Map for radiation myelitis.
AE, adverse effects.
Source: Asbell SO, Grimm J, Xue J, et al. Introduction and clinical overview of the DVH risk map. Semin Radiat Oncol. 2016;26(2):89–96. doi: 10.1016/j.semradonc.2015.11.005
30Validated models, in which clinicians can have some confidence, assist in predicting adverse effects of current regimens, making rational, patient-specific treatment decisions, and may be helpful in extending to new regimens, such as the moderate hypofractionated schedules with more than 5 fractions, such as 7 Gy × 10 and 7.5 Gy × 8, which are of interest in NSCLC SBRT (88). TCP and NTCP models can also be incorporated into plan optimization or plan evaluation algorithms (89). There were efforts for a few years to generate mechanistic, tissue architecture-based (serial or parallel) models of NTCP (79, 90) that would handle volume dependences, and a model termed the “relative seriality model” is often used in European publications (91). In North America, it is more common to use other multiparameter functions that capture dominant features of the DV response for various complications.
It is generally believed that NTCP, like TCP, increases monotonically from 0 for very low doses to 1 at a dose distribution with sufficiently high doses over sufficiently large volumes (conditions are deliberately explored only in animal studies). The function representing a complication dose–response is usually assumed to be sigmoidal, sometimes the logistic or log-logistic function. Dosimetric and clinical factors (e.g., gender, age, comorbid conditions, systemic therapies) that might affect complication risk may be identified through analysis of patient outcomes and validated through analysis of independent datasets. This is an ongoing process for all types of radiation therapy, not only SBRT. It is not uncommon for a model derived from one dataset to do poorly with a dataset from a different institution, even given similar prescription doses and treatment techniques. For example, two recent studies modeled radiation pneumonitis in patients with NSCLC treated with SBRT. Each used a model on the basis of the mean ipsilateral normal lung EQD2 with α/β = 3 Gy and had a moderate number of patients. Yet in one (92) the mean 2-Gy equivalent dose for 50% complications (NTCP = 50% at TD50) was 22.4 Gy and γ50 was 2.2, whereas for the other (93) the TD50 was 32.4 Gy and γ50 was 0.6. Differences in end-point scoring were likely responsible for much of the difference—but this example shows that NTCP models, even when published, should not be adopted without close inspection and validation. It is also not uncommon for available data to be so noisy that no coherent model can be found (this was the case in the QUANTEC reviews for radiation myelitis in the T-spine [70] and radiation-induced bladder complications [94]). Nonetheless, for many complications, there is enough agreement to provide clinically useful, though imperfect models for conventional fractionation (67) and the situation for SBRT is evolving toward a similar state.
A typical analysis starts with a dataset that, ideally, consists of dose distributions (DVHs for the OAR under study), complication outcomes, and other characteristics of the patients in the study that the authors think might be relevant. The DVH is sometimes reduced to a few key points (e.g., Dmax, V20, D05) but often more complex expressions that account for the entire DVH are used, as described in the following text. The most significant predictive variables are identified by increasingly sophisticated statistical outcome analyses, and these are often combined as the argument of a sigmoidally increasing function. This argument, Z, may be a single significant DV variable such as mean organ dose, or such a variable multiplied by a dose-modifying factor (e.g., for chemotherapy [95]) or a combination of significant variables determined by multivariate analysis (e.g., Z=p0 + p1 × DV1 + p2 × DV2 + p3 × [nondosimetric factor]). For an explicit application using DV variables for two different organs, see reference 83. The sigmoidal shape is versatile and convenient and, when there are enough data to discriminate, is a reasonable representation of the low to medium region of the reported OAR response (it is hard to test the high-NTCP region clinically for obvious reasons).
Model Functions
As with TCP, the log-logistic expression is one often-used function to predict the probability of normal tissue complication:
![]()
31For example, for spinal cord complications, Z could be Dmax (conventional fractionation) or BEDmax; for normal liver, Z could be the mean dose or the mean BED. In a general case, Z need not be dose—it can be Vdose or a combination of significant variables. NTCP is 0.5 at Z50 and k determines the steepness of the Z dependence at Z50.
The logistic function is also frequently used (for examples, see reference 83):
![]()
The probit function is increasingly used to describe a complication’s dose responses. Here, we have
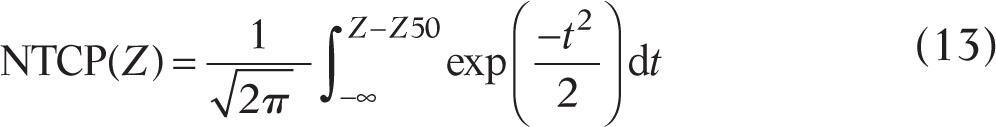
The Lyman Model
In the Lyman model (96), which is perhaps the most widely used NTCP model in North America, the upper limit of the probit function incorporates the effect of the complication’s volume dependence on complication probability. About 5 years after Lyman’s paper, Emami et al. (84) reviewed the literature from the “two-dimensional” era for 28 dose-limiting complications. They captured volume dependences through literature-based estimates of the doses for 5% and 50% incidence of each complication for uniform irradiation of the whole, two-thirds, and one-third of an organ (v = 1, 2/3, and 1/3), with the remainder receiving zero dose (84, 97) (Figure 2.10). This dose distribution, called “partial organ irradiation,” is not totally artificial; it is a reasonable approximation of the dose distribution from parallel-opposed beams. In a companion paper, Burman et al. (97) fit these six data points “by eye” to the Lyman model, where NTCP for partial organ irradiation of a volume v is
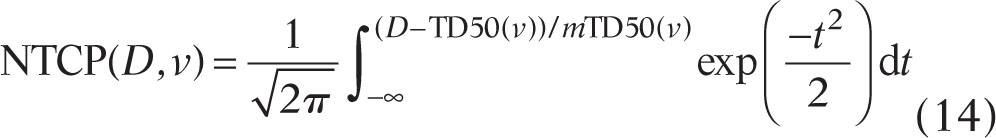
TD50(v), the dose at which NTCP for partial organ irradiation of volume fraction v is 50% (0.5), is given by a power law TD50(v) = TD50(1)/vn. One parameter of the Lyman model is the “reference volume,” which is usually the entire organ, so v is always ≤1. The Lyman model volume-dependence parameter, n, is always positive. Burman et al. restricted n ≤1, although there was no biological or mathematical reason to do so and some later studies have found n above 1. However, Burman et al. had an acceptable “by-eye” fit to the limited data available prior to 1991. If n is very small, vn varies weakly with v and the complication is “serial,” with a weak volume dependence. An example is radiation myelitis, for which n = 0.05. If n is close to or larger than 1, the complication has a strong volume dependence; an example is radiation pneumonitis for which Burman et al. (97) found n = 0.87 and many later analyses have found n = 1, implying that pneumonitis at conventional fractionation correlates with the mean lung dose. Figure 2.10 shows the n from Burman et al. (97) for partial volume 32dependences of some important complications The parameter m determines the steepness of the dose–response; γ50 = ((2π)1/2m)–1. For the fits of Burman et al. (97), m ranges from approximately 0.1 (γ50 ~ 4) to 0.27 (γ50 ~ 1.5).
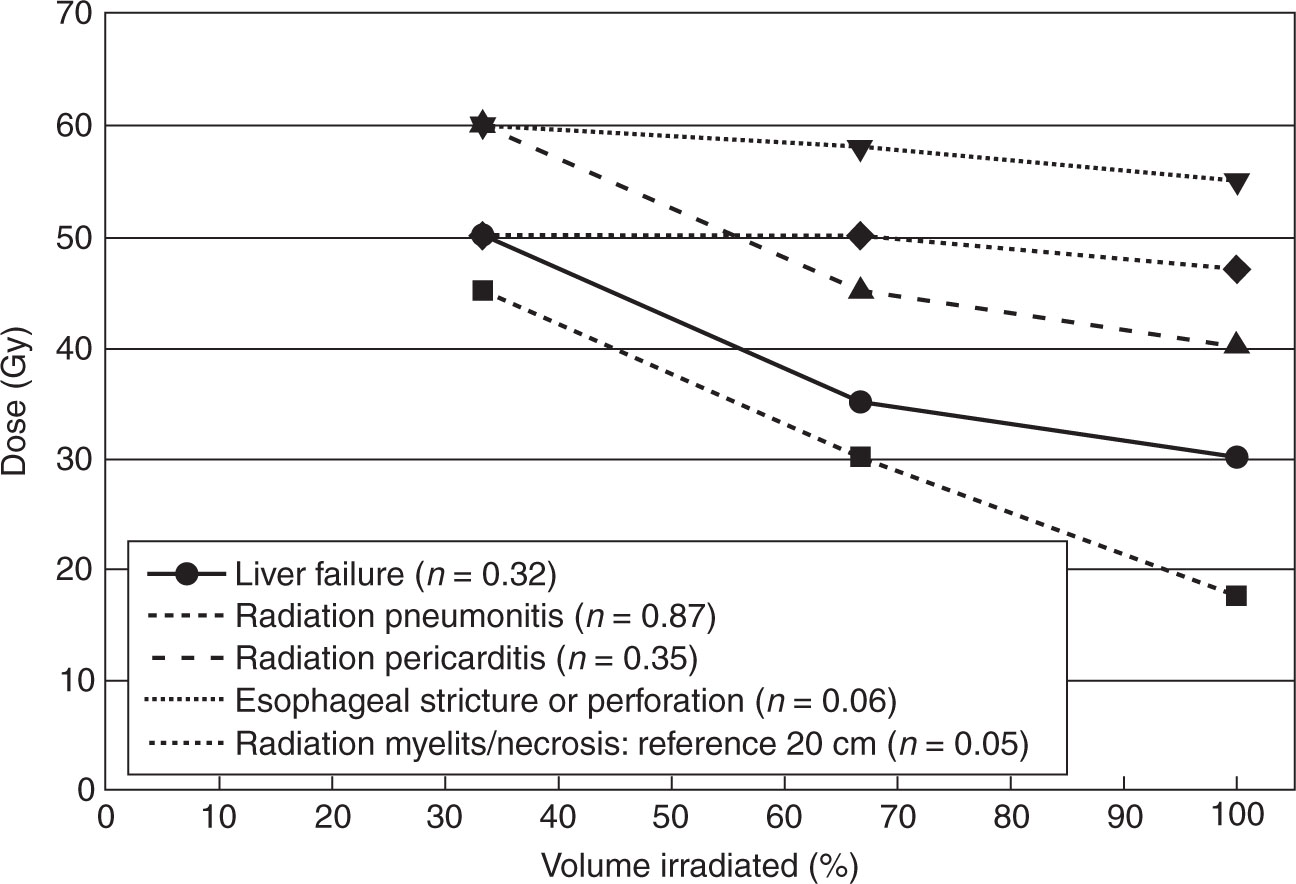
FIGURE 2.10 Lyman model volume dependences for partial organ irradiations according to reference (97).
To use the Lyman model for a plan that is more complex than partial organ irradiation, the DVH must be converted into an isoeffective single-step DVH, that is, a uniform dose to partial volume. Two “histogram reduction” schemes were devised to deal with general dose distributions where a volume fraction vi receives dose Di, as summarized by a DVH. The effective volume method converts the general case into a partial organ irradiation of a volume fraction veff to a reference dose Dm such that this partial irradiation has the same Lyman model NTCP as the true distribution. Here, veff = Σi(Di /Dm)1/n vi and Dm is often taken as Dmax (98, 99), although this choice is arbitrary and the prescription dose has also been used. In the upper limit of the probit integral, TD50(v) is set to ![]() .
.
A more common histogram reduction method is to convert the dose distribution to a uniform dose to the entire volume that has the same NTCP as the true dose distribution:
![]()
With this method, the upper limit in Eq. 14 is (Deff – TD50(1))/mTD50(1). Deff is the mean organ dose for n = 1, whereas small n favors the highest doses in the distribution.
The Lyman model is often applied to new data to refit the parameters for the original 28 complications or to apply the model to other complications. For applications to SBRT, some investigators convert the dose for each dose bin to a BED or an EQD2 (or EQD with a different reference dose) bin, but a surprising number of investigators do not.
The Relative Seriality Model
The relative seriality model (100) is widely used in Europe and is implemented on several planning systems. The basic premise is that normal tissues are a mix of serial and parallel components. However, the amount of mixture is determined by fitting outcomes to dose distributions rather than studying the microscopic construction of the organ. Thus, this model, like the Lyman model, is phenomenological, albeit with a different four-parameter function to express the DV dependence of a complication. Specifically, if a fraction vi of the reference volume receives a dose (or a BED) Di, then we have
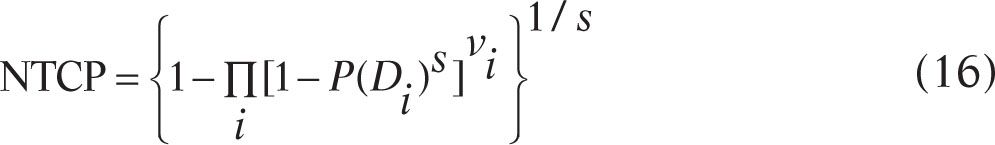
where P(Di) = 2−exp(eγ(1 − Di/D50))
The parameter s is called the seriality parameter: s = 1 describes the serial model of Niemierko and Goitein (101), whereas s is small for a complication that exhibits a strong volume dependence (a parallel-type complication).
Generalized Equivalent Uniform Dose
Niemierko recognized that the Deff as defined for the Lyman model is the EUD for normal tissues. He proposed that general volume dependences of radiation responses could be efficiently described for both OARs and tumors by a gEUD (66). The gEUD is quite unlike the earlier cell-survival-based EUD concept (65), and perhaps because gEUD captures important effects of volume dependences in a simple mathematical form that does not require a cell-based radiobiological model, gEUD is widely used. The gEUD volume dependence parameter is called a. For normal tissues, the gEUD a is the inverse of the Lyman model n. However, a is also allowed to be negative and can represent the EUD for TCP. Thus, for a general dose distribution, we have
![]()
A large value of a accentuates high-dose portions of the dose distribution; for a = 1, gEUD is the mean dose, whereas if a is negative, gEUD is sensitive to cold spots. For example, consider a simple dose distribution where the dose to 5% of a structure is 30 Gy, the dose to another 5% is 75 Gy, and the remaining 90% receives a dose of 60 Gy. gEUD is dominated by the cold spot in the dose distribution and gEUD = 34.8 Gy for a = –20. If a = 1, gEUD = 59.25 Gy, whereas if a = 20, gEUD = 65.2 Gy. gEUD can be used to rank dose distributions according to both relative tumoricidal efficacy and OAR sparing and can also be incorporated into optimization algorithms through terms that, by choice of the a parameter for an optimization structure, “push” only on selected points of that structure’s DVH (89). As with the Lyman model’s Deff, the “dose” from which gEUD is calculated can be replaced by BED 33or EQD, which is especially useful when dealing with hypofractionated treatments.
Two Unexpected Normal Tissue Responses to SBRT Treatments
In most applications, thanks to caution, image-guided radiation therapy (IGRT), and luck, the toxicity of SBRT treatments has been comparable to or even less than that of modern conventionally fractionated radiation therapy. But there have been a few surprises along the way, as seen from the following two examples.
Severe Complications in Early Days of Lung SBRT
Treatment of early stage NSCLC was pioneered in the early 2000s (102). Initially, the treatment plans were calculated without inhomogeneity correction and were normalized to give prescription dose at the periphery of the PTV with a dose distribution shaped so that prescription was approximately 80% of the central PTV dose. Non-coplanar beams, shaped to just cover the PTV (no margin to account for penumbra), were used to sharpen dose falloff in normal tissue. An institutional Phase I trial, without restriction on tumor location, found that 20 to 22 Gy × 3 fractions did not exceed the maximum tolerable dose and a Phase II trial with 70 patients followed. Actuarial local control at 2 years was 95%. However, the trial also produced a high toxicity rate, including six deaths (Grade 5) and eight Grade 3 or 4 pulmonary and other toxicities (103). High-grade toxicities were strongly associated with central or perihilar tumor location. The authors advised against using SBRT with this schedule for tumors in the “zone of the proximal bronchial tree,” which they defined as encompassing a 2-cm expansion of the proximal bronchial tree, thus including the major airways. In popular terminology, clinicians began to refer to this region as the “no fly zone” and RTOG trials 0236 and 0618 avoided treating tumors in this region. Of note, although bronchial stenosis has been reported in the treatment of central lung tumors to high doses, it is relatively uncommon with conventionally fractionated external beam treatment (104).
The 20 Gy × 3 regimen for central tumors is no longer in common use, and outcomes data from early trials have become subject to interpretation because the dose distributions were calculated using the pencil-beam algorithm without inhomogeneity correction. To evaluate the delivered treatments, retrospective analyses were performed to recalculate dose distributions (same beams, same monitor units (MUs)) with the analytical anisotropic algorithm (AAA) (105) or with Monte Carlo (MC). It was found that the original plan monitor units delivered, in reality (i.e., when recalculated with AAA), a lower PTV dose, because increased attenuation in the pencil beam algorithm with no corrections for tissue inhomogeneity was not sufficient to compensate for the effects of lateral electronic disequilibrium and lack of backscatter that were correctly handled by AAA or MC. Thus, the observed results—both good and bad—of the 20 Gy × 3-fraction prescription were because of a delivered dose that was slightly lower than expected from the original treatment plans. To obtain similar outcomes from plans done from the start with an advanced tissue inhomogeneity algorithm (now required by national protocols), the prescribed dose per fraction for 3-fraction treatments has been reduced, often to 18 Gy.
The current approach to SBRT for tumors partly within the “no fly zone” is cautious and uses more fractions for better normal tissue sparing without reducing the prescription BED (α/β = 10 Gy) below the 100 to 105 Gy that correlates with superior local control for NSCLC (Figure 2.8). RTOG protocol 0813 is a Phase I dose escalation followed by a Phase II efficacy trial using 5-fraction SBRT for patients with centrally located NSCLC. The maximum point dosimetric constraints for central structures shown in Table 2.2 were strictly enforced, whereas the volume maximum dose constraints were encouraged but not mandatory.
The Phase II results for the maximum protocol doses, 11.5 or 12 Gy × 5 fractions (BED 123.6–132 Gy) were reported as an ASTRO abstract in 2016 (106). There were two Grade 5 toxicities attributed to SBRT in the 11.5 Gy × 5 group and one in the 12 Gy × 5 group. Overall there were 6 G3+ toxicities of the 38 patients in the 11.5 Gy × 5 group and 7 of the 33 patients in the 12 Gy × 5 group, whereas 2-year local control in the two groups was statistically the same (89.4% and 87.7%). The toxicity rate did not exceed the trial’s “stopping rule” and its effect on the standard of care for such patients awaits further study and publications.
Chest Wall Pain and Rib Fracture in Lung Cancer SBRT
Chest wall pain (CWP) and rib fractures are rare complications of conventionally fractionated photon treatment of intact breast with tangents or other conventionally treated thoracic sites. A rib fracture incidence of 1.8% was reported in a study of 1,624 patients with Stage I to II breast cancer treated with tangents or a three-field technique from 1968 to 1985 (107). A dose response was noted with patients receiving a whole breast dose less than 50 Gy having a significantly lower rib fracture rate than those receiving ≥50 Gy. Rib fracture incidence was also significantly increased by chemotherapy and lower beam energy (4 MV vs. 6 or 8 MV). Pain without fracture was not reported and not all fractures were accompanied by pain.
34
However, as 3- to 5-fraction SBRT became a common treatment of early stage lung cancer and lung metastases, a surprisingly high incidence of CWP alone or with rib fractures, occurring in the first 1 to 2 years after treatment, was noted. There is some mechanistic understanding of radiation-induced bone complications (108) but the physiological origin of CWP without fracture is poorly understood. Although CWP is usually a transient complication that can be managed with nonprescription medicines, its effect on quality of life and the novelty of its common occurrence in the SBRT setting make it a topic of both clinical and academic interests. Murray et al. (109) reviewed 18 publications on thoracic SBRT (2,422 lesions). They found a median-reported CWP incidence of approximately 19% (range 6.1%–46.5%) for all reported grades, with a median of 1.2% (0%–17%) Grade 3+ for papers that separated these out. Incidence of rib fracture was reported in eight of these papers; fracture incidence was usually less than that of CWP and frequently the fractures were painless. Because the chest wall is not a well-defined anatomical structure, artificial structures (e.g., a 2- to 3-cm expansion outward from the ipsilateral lung–chest wall interface) are used for dosimetric evaluation, and absolute volume rather than relative volume metrics are often recommended. Several studies of rib fracture (110, 111) contoured multiple individual ribs in seeking a dose response.
Most studies of CWP are large retrospective reviews by single or collaborating institutions using their own data from modern treatment planning systems and follow-up standards. Some have been restricted to a single fractionation scheme but others have included 3, 4, and 5 fractions and at least five use biological correction, usually with α/β = 3 Gy. At least five studies summarize their findings in terms of a dose–response model from which the probability of CWP as a function of selected DV metrics could be calculated. In addition, obesity (body mass index) was reported as a risk factor in at least three papers. Most papers provide recommendations for treatment planning DV constraints, often limiting the chest wall volume receiving doses above 30 to 40 Gy as much as possible without compromising target coverage. The maximum dose, the highest dose to a small volume (1–5 mL), and the highest dose to 30 to 70 mL of the artificial chest wall structure have all been cited. Some clinicians advise using more fractions for patients with targets near the chest wall (112–114) and effects of 8-, 10-, and 15-fraction treatments remain to be analyzed. Figure 2.11 is a three-dimensional Risk Map of the DV and fraction number constraints that are suggested in five publications (115–119). Roughly, higher doses are associated with the 5-fraction regimens and smaller volumes. Although there is no single consensus on constraints that will prevent CWP, because the points on a structure’s DVH tend to be highly correlated, efforts to reduce one or more DVH points combined with judicious counseling of patients at increased risk because of tumor size or location or high body mass index (BMI) may be a clinically sufficient way to deal with this nonlethal complication.
35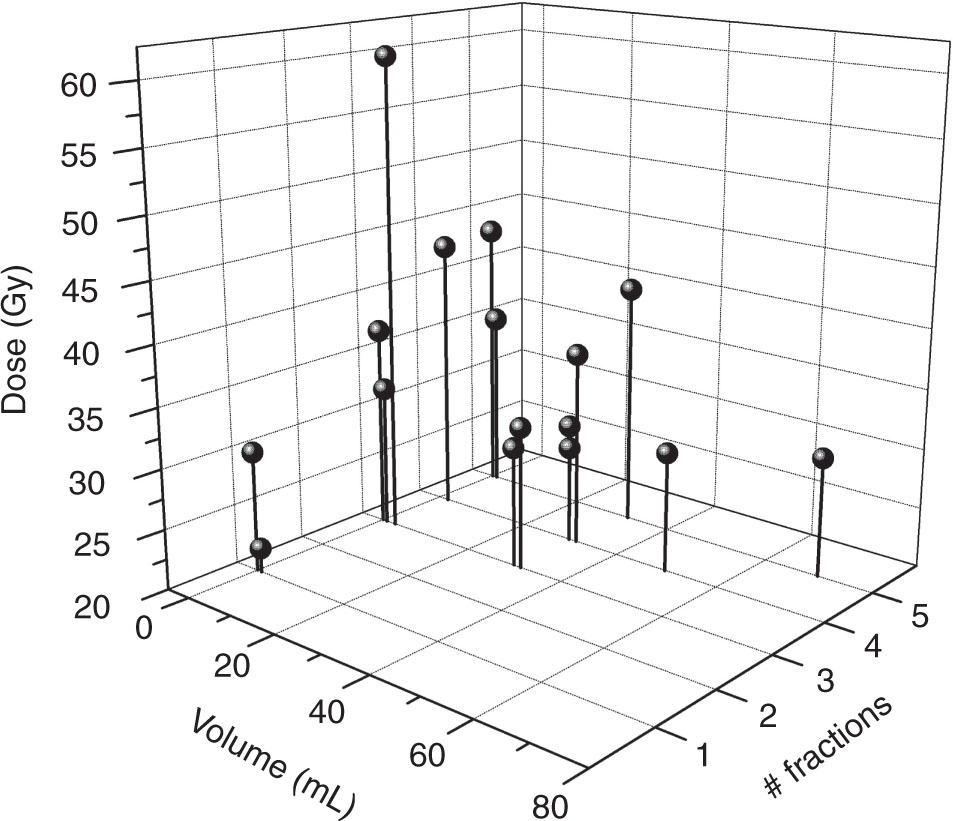
FIGURE 2.11 A three-dimensional Risk Map (dose, volume, number of fractions) for chest wall pain showing the recommended limits from five studies.
Sources: Adapted from Kimsey F, McKay J, Gefter J, et al. Dose-response model for chest wall tolerance of stereotactic body radiation therapy. Semin Radiat Oncol. 2015;26:129–134. doi: 10.1016/j.semradonc.2015.11.003; Benedict SH, Yenice KM, Followill D, et al. Stereotactic body radiation therapy: the report of AAPM Task Group 101. Med Phys. 2010;37(8):4078–4101. doi: 10.1118/1.3438081; Din SU, Williams EL, Jackson A, et al. Impact of fractionation and dose in a multivariate model for radiation-induced chest wall pain. Int J Radiat Oncol Biol Phys. 2015;93(2):418–424. doi: 10.1016/j.ijrobp.2015.06.014; Welsh J, Thomas J, Shah D, et al. Obesity increases the risk of chest wall pain from thoracic stereotactic body radiation therapy. Int J Radiat Oncol Biol Phys. 2011;81:91–96. doi: 10.1016/j.ijrobp.2010.04.022; Stephans KL, Djemil T, Tendulkar RD, et al. Prediction of chest wall toxicity from lung stereotactic body radiotherapy (SBRT). Int J Radiat Oncol Biol Phys. 2012;82: 974–980. doi: 10.1016/j.ijrobp.2010.12.002
CONCLUSIONS
SBRT presents radiation oncology with a paradigm change and a challenge. Relative to conventionally fractionated radiation therapy, for primary cancers, including early stage NSCLC and prostate cancer, it offers superior or at least equivalent complication-free cure, and for metastatic disease, it provides superior or equivalent palliation in a time frame that is far more manageable for patients and caregivers. The physics developments that contribute to SBRT’s success—advanced planning and delivery tools including superior image guidance—are well understood, as are physics improvements that might make it still more effective. However, there is a great deal of uncertainty about the basic radiobiology involved in the outcomes. Better understanding, even on a phenomenological level, of the biology that underlies SBRT successes is needed to safely and effectively apply such treatments to larger target volumes and to situations in which cure or long-term survival raises the risk of late complications.
REFERENCES
1. Hall EJ, Giaccia AJ. Radiobiology for the Radiologist. 7th ed. Philadephia, PA: Wolters Kluwer/Lippincott Williams & Wilkins; 2012.
2. Sachs RK, Hahnfeld P, Brenner DJ. The link between low-LET dose-response relations and the underlying kinetics of damage production/repair/misrepair. Int J Radiat Biol. 1997;72(4):351-374. PubMed PMID: 9343102
3. Wouters BG, Begg AC. Irradiation-induced damage and the DNA damage response. In: Joiner MC, van der Kogel A, eds. Basic Clinical Radiobiology. 4th ed. Boca Raton, FL: CRC Press; 2009.
4. Ling CC, Gerweck LE, Zaider M, et al. Dose-rate effects in external beam radiotherapy redux. Radiother Oncol. 2010;95:261-268. doi: 10.1016/j.radonc.2010.03.014
5. Joiner MC, Bentzen SM. Fractionation: the linear-quadratic approach. In: Joiner MC, van der Kogel A, eds. Basic Clinical Radiobiology. 4th ed. Boca Raton, FL: CRC Press; 2009.
6. Withers HR, Taylor JM, Maciejewski B. The hazard of accelerated tumor clonogen repopulation during radiotherapy. Acta Oncol. 1988;27:131-146. PubMed PMID: 3390344
7. Norton L. A Gompertzian model of human breast cancer growth. Cancer Res. 1988;48(24 Pt 1):7067-7071. PubMed PMID: 3191483
8. Horsman MR, Wouters BG, Joiner MC, et al. The oxygen effect and fractionated radiotherapy. In: Joiner MC, van der Kogel A, eds. Basic Clinical Radiobiology. 4th ed. Boca Raton, FL: CRC Press; 2009.
9. Okunieff P, Morgan D, Niemierko A, et al. Radiation dose-response of human tumors. Int J Radiat Oncol Biol Phys. 1995;32(4):1227-1237. PubMed PMID: 7607946.
10. Chapman JD. Can the two mechanisms of tumor cell killing by radiation be exploited for therapeutic gain? J Radiat Res. 2014;55:2-9. doi: 10.1093/jrr/rrt111
11. Goodhead DT. Initial events in the cellular effects of ionizing radiations: clustered damage in DNA. Int J Radiat Biol. 1994;65(1):7-17. PubMed PMID: 7905912.
12. Brenner DJ. The linear-quadratic model is an appropriate methodology for determining isoeffective doses at large doses per fraction. Semin Radiat Oncol. 2008;18(4):234-239. doi: 10.1016/j.semradonc.2008.04.004
13. McKenna FW, Ahmad S. Fitting techniques of cell survival curves in high-dose region for use in stereotactic body radiation therapy. Phys Med Biol. 2009;54:1593-1608. doi: 10.1088/0031-9155/54/6/013
14. Carlson DJ, Stewart RD, Semenenko VA, et al. Combined use of Monte Carlo DNA damage simulations and deterministic repair models to examine putative mechanisms of cell killing. Radiat Res. 2008;169:447-459. doi: 10.1667/RR1046.1
15. Lea DE, Catcheside DG. The mechanism of the induction by radiation of chromosome aberrations in Tradescantia. J Genetics. 1942;44:216-245.
16. Thames HD, Hendry JH. Fractionation in Radiotherapy. Philadelphia, PA: Taylor & Francis; 1987.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree