Robustness Quantification and Worst-Case Robust Optimization in Intensity-Modulated Proton Therapy

Fig. 10.1

Dose distributions in the transverse plane for a typical base-of-skull patient: The depicted distributions illustrate that the CTV-based robustly optimized plan (panels b, d) is insensitive to uncertainties relative to the PTV-based conventionally optimized plan (panels a, c). The prescription isodose lines (red lines) are heavily perturbed even within CTV (indicated by the red arrow). CTV, orange segment; brainstem, green segment; right temporal lobe, cyan; left temporal lobe, blue. The better normal tissue protection could also be seen by comparing the nominal dose distribution from the conventional optimization (panel a) and the one from the robust optimization (panel b)

Generally, the inter-fractional patient setup uncertainties are considered to be random and are incorporated by shifting the isocenter of the patient in the anteroposterior (A-P), superior–inferior (S-I), and lateral (R-L) directions by the same margin as is used for defining the PTV, yielding six dose distributions and the corresponding “influence matrices.” Range uncertainties for a single patient are systematic and propagate through the whole course of the treatment but are random for a patient population. They are incorporated by scaling the stopping powers by −3.5 and 3.5 % to generate two additional dose distributions and influence matrices corresponding to maximum and minimum proton ranges, respectively. Therefore in total there are 9 doses per voxel (the nominal dose plus 8 perturbed doses). Dose distributions are recalculated by a dose engine (either a commercial system like Eclipse^TM or an in-house-developed dose engine) for each of the eight scenarios. The recalculation of the dose distributions is tedious and time consuming, especially for the situations of range uncertainties since a correspondingly modified stopping power table has to be employed.

The above method is adopted in most operational proton centers for practical reasons. However, in order to account for the impact of the combined uncertainties, some groups proposed to use 21 doses per each voxel, i.e., for each of nominal, minimum, and maximum proton range, the isocenter of the patient is at the nominal position and rigidly shifted in the A-P, S-I, and R-L directions respectively, yielding 21 dose distributions (7 per proton range) [18, 19].

Based on the recalculated dose distributions as described above, so far three robustness quantification methods have been published:

Worst-case analysis [20, 21]: We can extract the highest and the lowest dose values in each voxel from the original and the perturbed dose distributions, forming a hot dose distribution with the highest values and a cold dose distribution with the lowest values. The dose distributions derived in this way provides an estimate of the robustness of the delivered dose to spatial and range uncertainties [22]. Please note that the resultant dose distributions are unrealistic (please see the Sect. 10.4). The original DVH of each structure from the nominal dose distribution is overlaid by a shaded area that was bounded by the DVHs from the cold and the hot dose distributions obtained from the robustness analysis. The width of the DVH bands corresponds to the plan robustness for the structure indicated (Fig. 10.2).

Fig. 10.2

Worst-case robustness quantification of the 3 F-MFO, 3 F-SFO, and 2 F-SFO (F is used for fields) plans for a head and neck patient: The solid lines are DVHs for the nominal doses, and the shaded areas (the bands) are bounded by the DVHs for the cold and hot doses obtained from the robustness analysis (This figure is from Fig. 2 of Quan et al. [21])

Bands of DVHs [23, 24]: To evaluate or compare IMPT plans, a robustness quantification technique is used that displayed the envelope of all dose-volume histograms (DVHs) in band graphs of all the dose distributions associated with the corresponding range or setup uncertainties. For convenience, the DVHs derived by choosing the nominal dose of a voxel are also displayed in the robust quantification. The width of the DVH bands is also used to indicate the plan robustness for the structure (Fig. 10.3).

Fig. 10.3

Robustness quantification using bands of DVH: Color wash represents the DVH bands for dose distributions covering all setup and proton range uncertainties for CTV and various organs for the robustly optimized plan (right column) and the PTV-based plan (left) for the non small cell lung cancer (NSCLC) case. The solid lines are the DVHs for the nominal dose distribution (i.e., without consideration of uncertainties). The narrowness of CTV band for the robustly optimized plan indicates improved robustness. At the same time, the sparing for the esophagus, spinal cord, and normal lung is perceptibly improved (This figure is copied from Fig. 1 of Liu et al. [23])

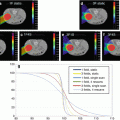
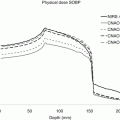
Robustness quantification using root-mean-square-deviation-dose-volume histograms (RVHs) [18, 19, 25] (analogous to the error-bar volume histograms [EVHs] proposed by Albertini et al. [26]): The root-mean-square dose deviation (RMSD) of voxels is calculated as the square root of the sum square of the differences between the dose calculated under the uncertainty scenarios and the nominal scenario and the mean dose of those 9 (or 21) doses. This was then used to construct the RVH, which represents the relative volume on one side (vertical axis) and the dose deviation on the other (horizontal axis) (Fig. 10.4). This RVH plot captures the overall effect of uncertainties on the dose to a volume of interest that is analogous to the dose-volume histogram (DVH) used for assessing the nominal plan. We further simplified the RVH to compare the robustness of two plans by calculating the area under the RVH curve (AUC), which gives a single numerical measure of the plan’s robustness for a given volume of interest and can be easily incorporated into the paired statistical tests for comparison: the smaller the AUC, the more robust the plan is for the structure between competing plans. Compared to the other methods, the RVH gives more quantitative information of the robustness of the plan. For example, the point in Fig. 10.4 as indicated by the arrow shows that 40 % of CTV from the robustly optimized plan (red solid curve) has the root-mean-square dose of at least 2.5 Gy[RBE].

Fig. 10.4

RVH curves derived from the robust plan (solid lines) and the PTV-based plan (dashed lines) for a head and neck cancer patient: Each curve was normalized by the total volume of the corresponding organ. RVH AUCs for the robustly optimized plan were smaller than those for the PTV-based plan, indicating that AUCs can be useful for relative comparisons of the plans in terms of robustness (This figure is copied from Fig. 2 of Liu et al. [19])

Park et al. proposed a statistical method [27] by performing a more comprehensive simulation to account for the dose under uncertainties, in which the dose was recalculated 600 times per given plan under the influence of random and systematic setup errors and proton range errors. On the basis of simulation, the probability of dose variations was determined and the expected values and standard deviations of DVHs were calculated. The uncertainties in dose were spatially visualized as a probability map of failure to target coverage or overdose of critical structures.

These robust quantification tools can be applied in the clinic to help physicians and physicists judge whether IMPT plans are acceptable. We should emphasize that the advantages of the worst-case methods described here do not require a detailed model for the considered uncertainties [8, 20] and do not need to consider a large number of uncertainty scenarios.

10.3 Worst-Case Robust Optimization

In this section, we will discuss the robust optimization (especially the so-called worst-case robust optimization) and its application in IMPT planning. During the last several years, there is significant progress in this area due to efforts worldwide. A few robust optimization techniques have been reported to be effective at compensating for setup and range uncertainties in IMPT planning [8, 9, 23, 28–31]. For example, Unkelbach et al. [9] showed feasibility of probabilistic robust optimization that requires large samples of perturbed dose distributions. Chen et al. [28] included the plan robustness in the multiple criterial optimizations (MCO) by navigation in the Pareto surface to find the compromise between the plan quality and plan robustness. Fredriksson et al. [29] suggested a minimax optimization method that significantly reduces the number of required dose samples by considering extreme yet realistic dose distributions. Pflugfelder et al. [8] showed that similar optimization results can be achieved by considering the theoretically worst-case dose distribution that is derived by assigning each voxel with the lowest (for target volume) or highest (for organs at risk) dose from only 8 sampled dose distributions calculated under extreme situations. The resulting treatment plans showed reduced sensitivity to uncertainties.

During the last several years, we have developed our own worst-case robust optimization methods [23, 30]. The methods we used to design and compare robustly and conventionally optimized plans differ from those used by many other investigators [8–11]. A modification of the objective function to penalize hot spots within the target, which could potentially occur due to range uncertainties, leads to improved target dose homogeneity. The objective function value for a given iteration is computed using the “worst-case dose distribution” [20]. The worst-case dose distribution was represented by the minimum of the 9 (or 21) doses in each voxel in the CTV and the maximum of the 9 (or 21) doses in each voxel outside the CTV. This is analogous to using the PTV dose distribution for photons, which implicitly represents the worst-case dose distribution for the CTV. Our robust optimization approach inherits the simplicity of worst-case robust optimization and does not require a detailed model for uncertainties.

It is important to note that in our worst-case robust optimization the optimization target is chosen to be CTV, rather than PTV. No geometrical margin is used; rather, uncertainties are considered and accounted for in the optimization algorithm. Although robust optimization does not directly aim to minimize the dose delivered to normal tissues in the nominal scenario (without any uncertainties considered), direct targeting the CTV instead of the larger PTV improves plan quality compared to conventional PTV-based optimization [18, 23, 30, 32].

IMPT optimization, in particular robust IMPT optimization, is highly CPU time and memory intensive. The memory requirement to compute influence matrices is substantial even in non-robust IMPT treatment planning. This is due to the following reasons: (1) Spatially dense beamlets may be needed to achieve desired dose distribution in highly inhomogeneous patient anatomies. (2) A fine dose grid in the dose calculation is needed to accurately reflect the steep dose gradient near the rapid fall-off region of the proton dose distribution [33]. (3) The number of energy layers used in the treatment beams often reaches 50 in a reasonably complex IMPT plan to form a wide enough spread-out Bragg peak (SOBP) to cover the target from the proximal edge to the distal edge. (4) The incident protons due to scattering along the beamlet path may spread over a large region. (5) Secondary particles from nuclear interactions in the medium have a much wider angular distribution than the primary protons [34]. The latter two issues cause the lateral dose distribution of a proton beamlet to be markedly different from a Gaussian distribution. While deviations from Gaussian distributions due to these factors are seemingly negligible, the sum of the contributions from all the distant beamlets can be up to 15 % of the total dose and must be accounted for to ensure the accuracy and validity of the optimized dose distributions [35, 36]. Better accuracy of the lateral dose distribution of one proton beamlet is, however, achieved at the expense of larger memory usage than with simple Gaussian distributions (about 30 times larger). Therefore the amount of data to be computed during IMPT treatment planning increases by one to two orders of magnitude, requiring substantial memory and computation time [4].

What is more, robust optimization for IMPT is even more challenging in computation time and memory usage since many more influence matrices are needed to include the impact of setup and range uncertainties in the optimization. Beam angle optimization and 4D robust and RBE-weighted optimization for IMPT are even more challenging in terms of computation time and memory usage since even more influence matrices need to be included in order to model the impact of uncertainties in the optimization, and on-the-fly RBE calculation is extremely time consuming. The resultant influence matrices, which are stored in the memory in the form of single precision floating numbers for efficient optimization implementation, easily consume more than 500 GB memory.

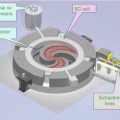
Due to the rapid development of parallelized computation via message passing interface (MPI) and CPU-clustered supercomputers, ultrafast and memory-limit-free implementation of robust optimization is now feasible. To achieve acceptable optimization times and meet memory requirements, we parallelized our robust optimization in the beamlet domain using memory-distributed parallelization on a large multiprocessor system (Fig. 10.5). All beamlet computations are dynamically allocated and distributed to the processors almost uniformly. Every processor handles the dose calculation of each dose voxel in volumes of interest for a group of beamlets belonging to a given beam. A compressed sparse matrix format is used to conserve memory for every processor. Our efficient method essentially has no memory limit and can easily be expanded to explore more demanding problems in the future. The optimization was performed using the limited-memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) method [37] included in the optimization software OPT++ [38].

Fig. 10.5

Diagram of implementation of our parallelized large-scale worst-case robust optimizer. The optimizer is parallelized on the beamlet domain and uses the L-BFGS algorithm

We are in the process of implementing robust IMPT optimization clinically at Mayo Clinic. Our approach has been used the University of Texas MD Anderson Cancer Center (MDACC) Proton Treatment Center at Houston (PTC-H) to generate robust IMPT plans to treat complex lung cancers. Fig. 10.6 shows the clinical work flow for robust optimization at MDACC. Steps in yellow are done in Eclipse^TM (Varian Medical Systems, Palo Alto, California), except the steps in white. First a plan will be generated in Eclipse^TM. The generated plan related files, namely, CT files, RT structure files, and the associated dose-volume constraints will be exported to the in-house-developed robust optimization software. During robust optimization (i.e., the step in white), the fluence map will be modified by the robust optimizer to generate a robust optimal plan. The robust plan is reimported to Eclipse^TM for the final dose calculation. DICOM files are used for communication between various pieces of software.

Fig. 10.6

Work flow chart of applying our worst-case robust optimization in MD Anderson Cancer Center Proton Treatment Center in Houston: Every step in yellow color is done in a commercial treatment planning system, Eclipse^TM with DICOM as the interface. The step in white color is the robust optimization step done in an in-house-developed worst-case robust optimizer. Patient data are de-identified

We have successfully applied our robust optimization to several disease sites (H&N, the base of the skull, the lung, and the prostate) for populations of patients [18, 25, 32] in IMPT planning studies [23, 24, 32]. To date approximately 100 patients have been studied using our system with satisfactory results. We have demonstrated that robustly optimized dose distributions are significantly less sensitive to setup and range uncertainties than the conventionally optimized PTV-based dose distributions. An important finding of our work is that robust optimization may also result in improved quality of plans in terms of greater sparing of normal tissues and more homogeneous target dose distributions [18, 19, 23, 25, 30, 32], which is consistent with the results by other groups [29, 39].

10.3.1 How to Account for Respiratory Motion

IMPT for targets in thorax is further complicated by intra-fractional respiratory motion. Intra-fractional organ motion may also cause significant changes in patient geometry [13] and, consequently, in planned dose distributions. The interplay effect of dynamic delivery and tumor motion has been reported to degrade the quality of the resulting dose distribution, particularly in IMPT [40–47]. Furthermore, it has been shown that the pattern of breathing motion seen at the time of simulation may change during treatment [48], which has been reported to seriously perturb the resulting dose distribution in IMRT [49]. Fortunately, the availability of respiration-correlated 4D CT has yielded a better understanding of the amplitudes and characteristics of anatomy motion due to breathing [50, 51]. In order to account for respiratory motion, an internal gross target volume (IGTV) is generally formed to encompass the extent of gross target volume (GTV) motion in all phases using four-dimensional computed tomography (4D CT). The IGTV is then expanded to form internal target volume (ITV) (ICRU 1999) [52] by an additional margin (e.g., 8 mm) to account for subclinical microscopic disease. Techniques such as breath hold, gating, and tumor tracking can be used to mitigate the effects of large amplitude respiratory motion. The methods of breath holding, gating, and tumor tracking can be unreliable, difficult for patients to tolerate, and technologically demanding and may prolong the treatment time, while the ITV method may deliver more dose than is necessary to the healthy tissue surrounding the tumor [52]. In addition, the change in tissue density due to respiratory motion was generally accounted for by the use of averaged 4D CT and integrated density override of the GTV (over all phases). Kang et al. [13] demonstrated that this method was effective in preserving target coverage under the influence of respiratory motion for PSPT, while its effectiveness in IMPT is still under investigation.

We did the worst-case robust optimization in a population of lung cancer patients [25]. We found that although our worst-case robust optimization method did not directly account for respiratory motion in the optimization algorithm, it was still superior to the conventional PTV-based optimization. We speculated that the effects of respiratory motion might possibly be translated into setup and range uncertainties, which could be possibly mitigated by our method [25]. The non-serious interplay effect from our worst-case robust optimization might be due to the fact that the spot spacing is similar to the tumor motion magnitude [47] since the patients included in the study are all from an institution protocol with the tumor motion less than one specified threshold (5 mm). Our method would be an acceptable solution to mitigate the influence of residual respiratory motion combined with setup/range uncertainties in IMPT to treat lung cancer with deep breath hold or beam gating. Appropriate repainting technique [44] might appear necessary to further minimize or eliminate the consequences of interplay effects if the spot sizes are smaller. Therefore, this planning approach could have a large, immediate clinical impact as several centers either currently treat or plan to treat lung patients using breath hold or beam gating. However, motion reduced the effectiveness of our methodology [25]. Thus, 4D robust optimization for IMPT might be one of the possible eventual solutions for treating lung cancer because it could potentially reduce the influence of motion uncertainty (i.e., irregular organ motion) as well. Some preliminary results are shown in Fig. 10.7. We refer the readers to Sect. 10.5.